桩基础动阻抗函数计算方法研究

2016-09-19韩泽军胡志强

水利与建筑工程学报 2016年4期

王　朋,韩泽军,胡志强

(1.大连理工大学海岸与近海工程国家重点实验室, 辽宁大连 116024；2.大连理工大学工程抗震研究所, 建设工程学部水利工程学院, 辽宁大连 116024;3.华南理工大学土木与交通学院，广东广州 510641)

桩基础动阻抗函数计算方法研究

王朋1,2,韩泽军3,胡志强1,2

随着现代工程建设规模的扩大，桩基础得到广泛的应用。针对成层地基上的桩基础，采用两种方法计算了桩基础动阻抗函数：子结构法即离散桩体，采用混合数值算法求解半无限成层地基的格林函数，并结合容积法进行求解；直接法即对桩及桩周围有限域土体进行离散，在边界处施加黏弹性人工边界，进行桩-土系统的整体求解。前一种方法中所采用的混合数值法，该方法计算精度高，且适用于复杂水平成层地基，后一种方法则计算方法简单，适用于大型群桩系统。在数值算例中，计算了半无限地基中单桩、2×2桩基和4×4桩基以及多层水平成层地基中带承台的桩基础的阻抗函数，验证了方法的精度，并讨论了网格尺寸、计算范围选取对计算精度的影响。研究结果对桩基和施工有一定指导意义。

动力相互作用；桩基础；阻抗函数；混合数值法；粘弹性人工边界

对于建设在软弱地基上的码头、桥梁以及高层建筑等工程，为了控制结构沉降和提高地基承载力[1]，常采用桩基础的地基处理形式[2]。历次世界大地震中，均出现了各类桩基础的严重破坏现象[3]，为保证这类结构安全，需要进行考虑土-桩-结构动力相互作用分析[4]，而群桩阻抗函数的计算是其中一个重要的课题。对于动力荷载，如上部结构引起的振动或地震，桩体对基础的动力刚度也将产生显著影响，但由于桩基与桩周围土体的振动特性不同，波在两种介质之间反复振动以及群桩效应等使群桩阻抗函数的计算变得十分复杂。Novak等[5]引入平面应变假设首先进行了单桩阻抗函数研究；Kaynia等[6]对均质地基中群桩的动力阻抗进行了分析，其结果被视为严密解答，成为众多算法对比校核的依据；Gazetas和Mrakis等[7-8]采用动力相互作用系数较好地考虑了群桩效应的影响；蒯行成等[9-10]采用动力文克尔地基梁模型提出了计算层状介质中群桩的水平、竖向和摇摆动力阻抗函数的简化方法；蒋通等[11]人采用薄层法计算了层状地基中基础的阻抗函数。

近年来，林皋等[12]提出了一种高效而精确的混合数值法，可求解层状半空间任意形状基础的格林函数，本文根据子结构法中求解埋置基础动力刚度的容积法，将这一方法推广用于计算层状地基中桩基阻抗函数。同时，本文也应用了直接法，通过在边界施加黏弹性人工边界条件来计算桩基础的动力刚度，该方法原理简单、易于程序实现，对于大型群桩、含有夹层、孔洞等复杂地基情况，以及考虑土体介质和桩-土交界面非线性变形特性的情况，具有较好的适应性。

本文通过计算半空间弹性地基和水平成层地基上中单桩、2×2、4×4群桩基础的阻抗函数，验证了这两种方法的精度和适用性。

1　基础阻抗函数计算

基础阻抗函数定义为在基础顶面某一指定方向施加一单位幅值的谐振运动，在基础顶面产生的谐振荷载的幅值，可以写作K=k+ia0c的形式，其中，k和c分别为阻抗的刚度项和阻尼项，a0=ωd/V是无量纲频率，V为土层的剪切波速。

1.1子结构法-地基格林函数的混合数值算法和容积法组合求解

对于层状半无限空间，混合数值算法首先通过Hankel变换将时域-空间域的波动方程变换成频率-波数域内多层地基上的波动方程，再通过引入位移对偶向量，运用精细积分算法[13]求解，进而求得地基中任意点的格林函数，详细推导见文献[14]。

对于层状地基中采用桩基础的情况，计算模型如图1所示。利用层状半无限空间中的格林函数，采用容积法可求出桩基础的动力刚度，对于刚性承台，可再通过动力凝聚，获得基础顶部的阻抗函数。在容积法中，首先将地基-桩基础体系分为桩体p与层状半空间地基中除去桩体后的地基g两部分的叠加，后者又由层状半空间地基减去与桩体所占位置相同的土体e部分后得到，如图2所示。各区域的动力阻抗之间也有类似的关系。计算时，对桩体p和位于相同位置的开挖土体e采用相同的离散网格。

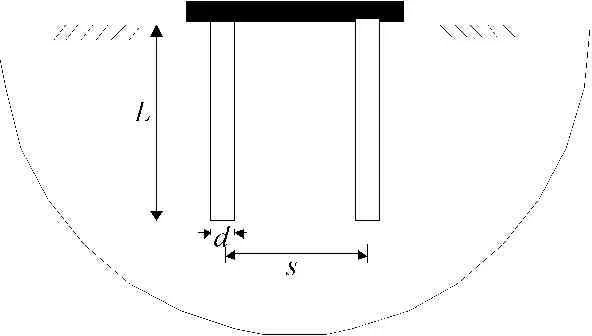
图1　弹性半空间中的群桩基础

图2群桩基础容积法原理

在频域内，桩基础上各节点所承受的节点力与节点位移的关系为

{P}=[S]{U}

(1)

式中：{P}、{U}为节点力和节点位移，[S]为地基-桩基础体系的动力刚度矩阵。由容积法可得动力刚度矩阵[S]为

(2)

当承台刚度远大于桩体刚度时，承台可看作是刚性的，对于此种情况，可将桩基分为桩顶部和桩身，动力刚度矩阵可写成如下的分块形式，即

(3)

其中下标1表示桩顶部分，下标2表示桩身部分，故式(1)可写作

(4)

由于桩基节点中只在桩顶节点部分受外荷载作用，采用静力凝聚的方法，由式(4)可得桩头节点与位移的关系如下：

{P}1=[R(iω)]{U}1

(5)

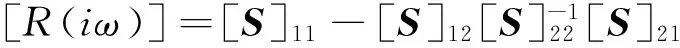
根据力的平衡条件，桩基承台上作用的集中荷载{P}B与桩头所承受的外荷载{P}1之间有以下关系

{P}B=TT{P}1

(6)

其中T为转换矩阵，如下式所示

T=[T1T2…Tn]T

(7)

其中坐标点(x0,y0,z0)为参考点坐标。

因为刚性承台与地基完全相连，所以在集中荷载作用下桩顶节点位移幅值{U}1与承台参考点位移幅值{U}B需满足

{U}1=T{U}B

(8)

其中刚性基础有6个刚体自由度，即

{U}B=[ΔxΔyΔzφxφyφz]T

(9)

由上述公式可得刚性承台参考点荷载与其位移之间的关系为

{P}B=TT[R(iω)]T{U}B

(10)

1.2直接法-外边界施加粘弹性人工边界条件

这一方法中，需对桩基础、及其附近土体进行有限元离散，并在边界处施加人工边界条件。然后，通过在基础顶面施加不同频率的指定位移模式，进行谐分析求出相应的动刚度(如图3所示)。该方法可以较为全面地考虑地基中存在的各种不均匀性，如孔洞、夹杂、非水平成层等情况，但动刚度计算精度还要受到人工边界条件精度的影响。这是因为大多数人工边界基于某种特定形式的波动建立起来，而在复杂地基下，外行散射波场很复杂，因此难以获得能够模拟以不同角度入射、不同波动类型的外行波向无穷远传播的人工边界。本文采用以阻尼器和弹簧表示的黏弹性人工边界条件[15]，该边界条件具有形式简单，物理意义明确，程序易于实现等优点。

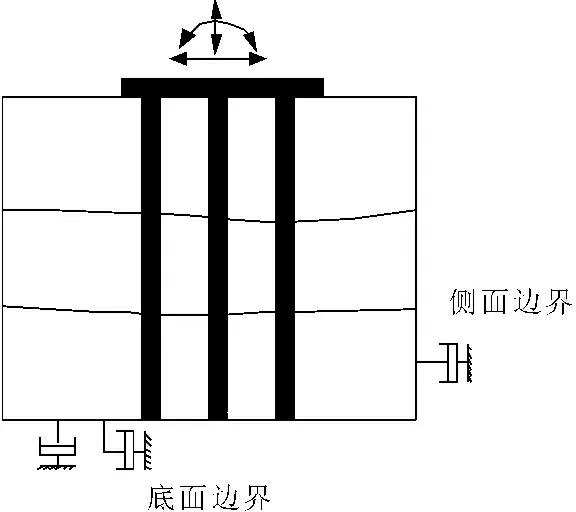
图3黏弹性人工边界条件计算模型

黏弹性人工边界是一种应力边界条件，作用在边界上的面力σ可表示为

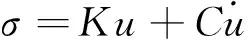
(11)

其中K和C可看作是弹簧和阻尼系数，取值如下：

(12)

式中：G、ρ、c分别为土层的剪切模量、质量密度和波速；R表示散射源至模型边界的距离；α和c的取值见表1。

表1　黏弹性人工边界条件中系数取值[16]

2　数值算例

2.1半无限地基中桩基础的地基阻抗函数

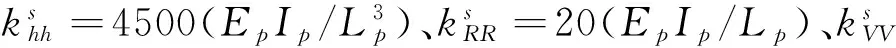
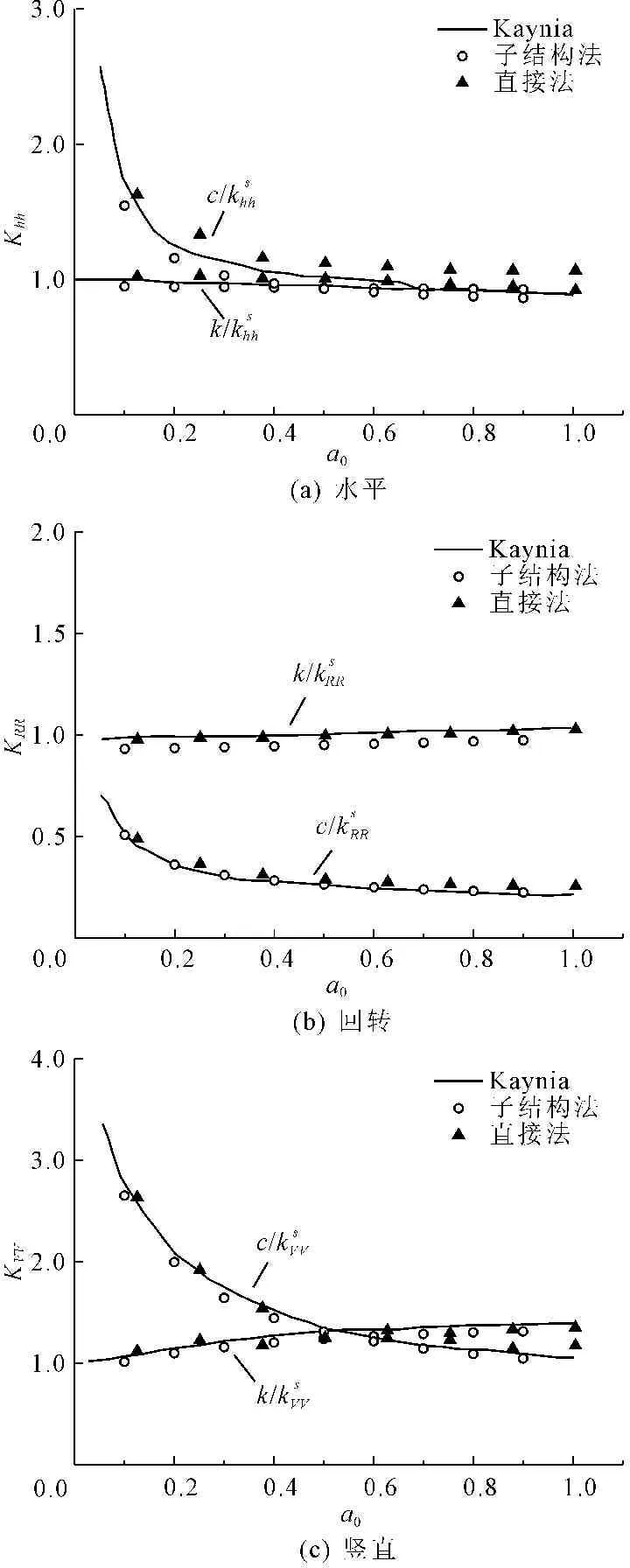
图4半无限地基中的单桩阻抗函数

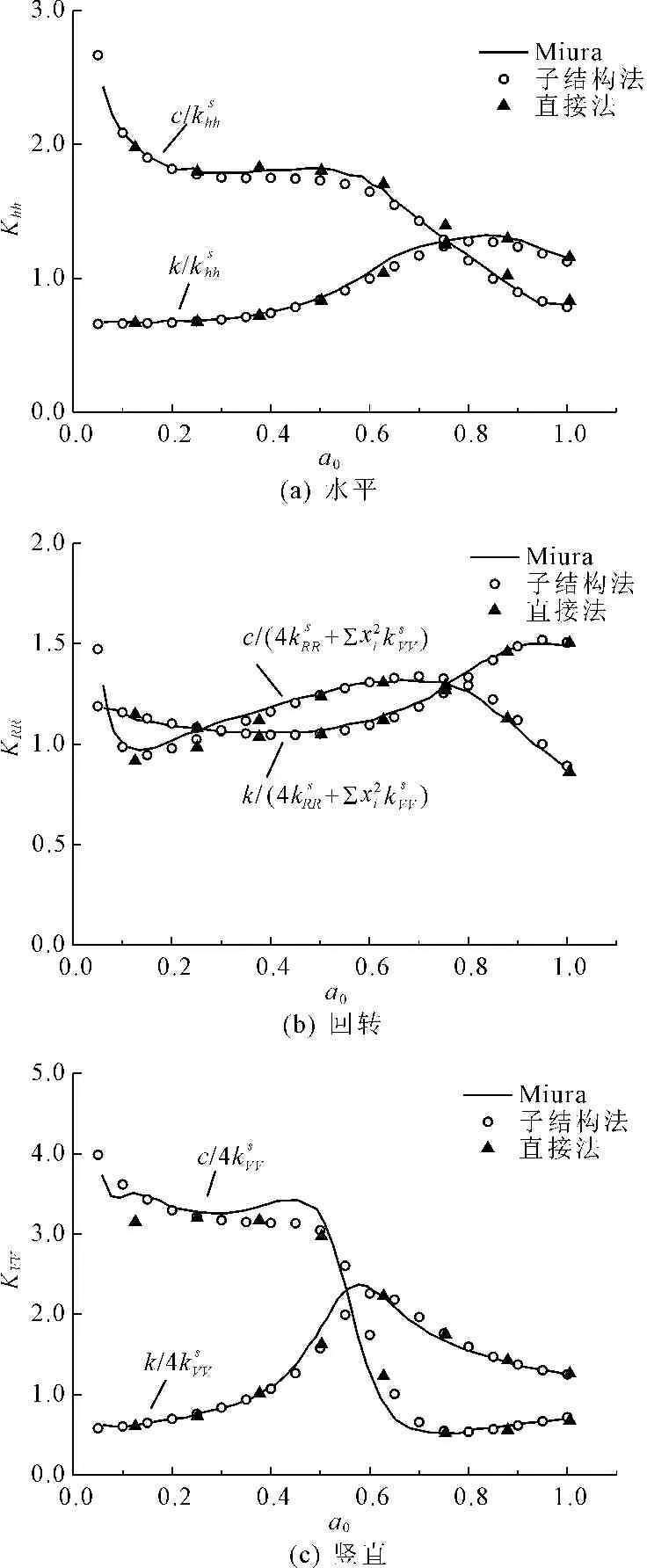
图5半无限地基中2×2群桩的地基阻抗函数

采用直接法计算时，对于单桩基础，计算模型范围为40m×40m×30m，竖向网格尺寸为1m，水平方向最大网格尺寸为1.9m；对于2×2群桩基础，计算模型范围为60m×60m×30m，竖向网格尺寸为1m，水平方向最大网格尺寸为0.9m；对于4×4群桩基础，计算模型尺寸为60m×60m×30m，竖向网格尺寸为1m，水平方向最大网格尺寸为0.85m，模型节点个数为179 918，单元个数为168 824。由此可见，虽然利用黏弹性人工边界有着计算简单等优点，但是为了满足计算精度，需要采用较大的计算模型，而且网格尺寸还需满足一定条件，在实际工程应用时还需要采取措施提高计算效率和精度。

图6基于黏弹性人工边界的4×4群桩阻抗函数

在采用子结构法计算时，对于单桩基础，当竖直方向网格尺寸为0.5m，当竖向采用1m网格时，计算结果中水平、竖直方向阻抗函数实部和虚部均偏小，加密竖向网格，使得竖向网格尺寸减小为0.5m，结果与文献中结果十分接近。对于2×2群桩基础，当竖向网格尺寸为0.5m进行计算时，所得水平、回转和竖直阻抗函数虚部均偏小，当加密竖向网格尺寸至0.25m时，可以取得较好结果。这说明网格尺寸对计算结果的精度有着较为重要的影响。

2.2层状半无限地基中群桩基础的地基阻抗函数

本例题针对水平成层半无限地基中的2×2群桩-刚性承台基础[19]计算了阻抗函数，其中承台尺寸为4.4m×4.4m×4m，桩直径d=0.6m、Lp=7.5m、桩间距s=2.2m，密度ρp=2 400kg/m3，泊松比vp=1/6，弹性模量Ep=2.4×1010N/m2，不考虑桩体的阻尼。层状地基参数见表2，不考虑基础底面与地基接触，分别用子结构法和直接法计算了群桩-刚性承台基础的水平、回转和竖直地基阻抗函数。其中，采用子结构法计算时竖直方向最大网格尺寸为0.3m，直接法竖向方向最大网格尺寸为0.6m。文献的计算结果对比如图7所示。由图7可见，采用两种方法计算得到的基础刚度的数值和变化趋势较为吻合；对于水平和回转刚度，本文计算值与文献[19]计算结果较为一致，但竖直刚度相差较大。

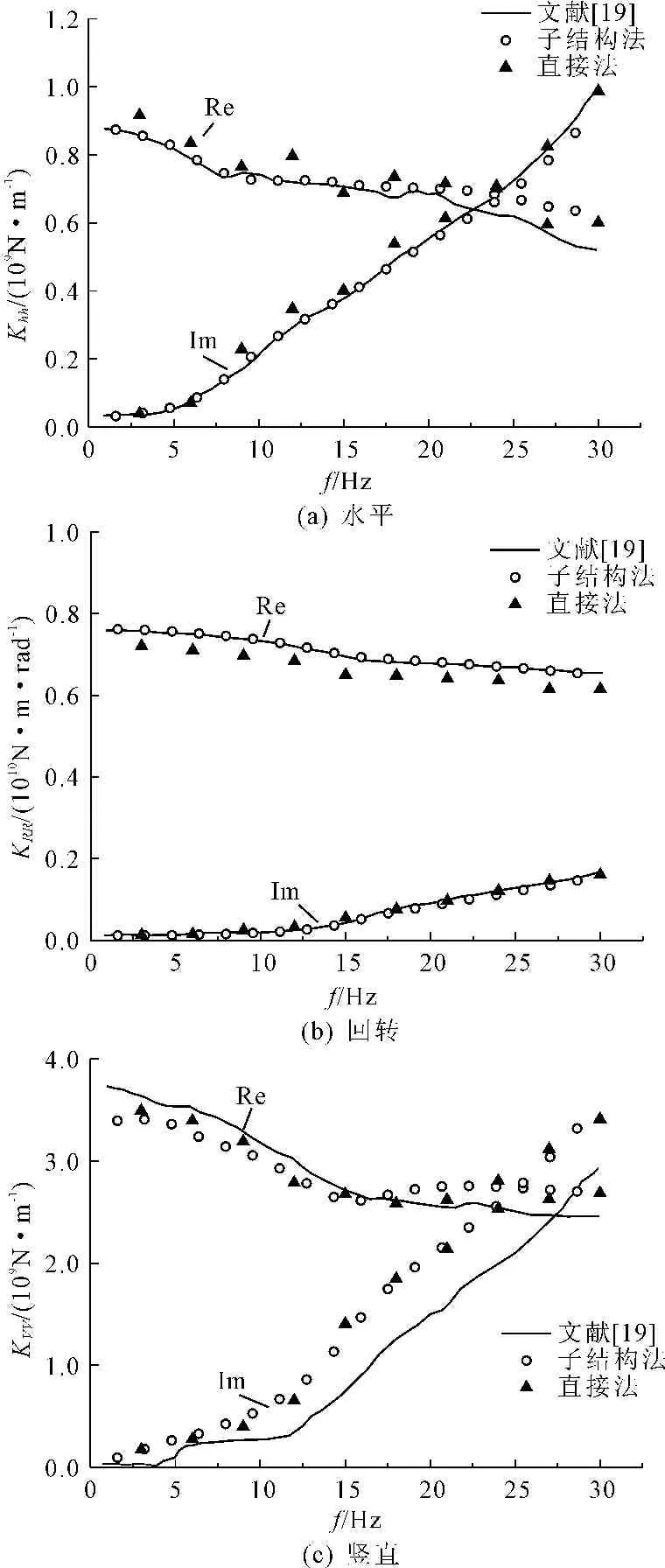
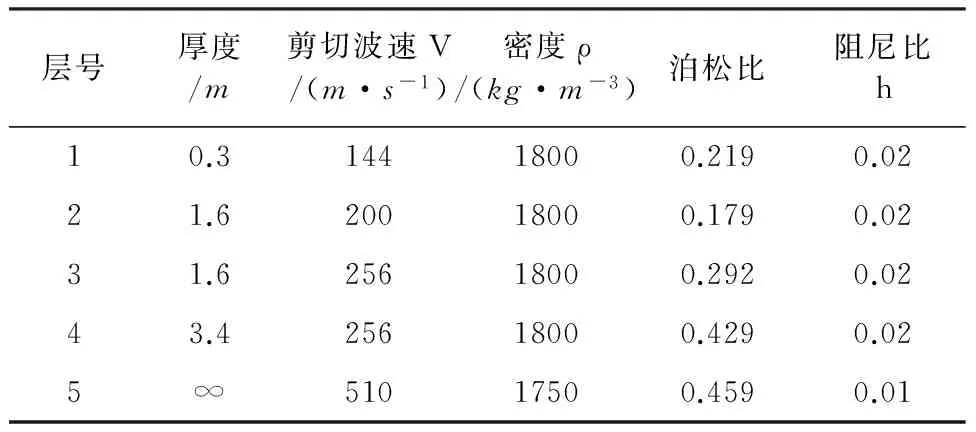
图7　群桩基础的地基阻抗函数

3　结　论

本文采用子结构法和直接法计算了桩基础的阻抗函数。

(1) 在子结构法中，利用混合数值法能够准确计算出水平成层地基格林函数的优点，将其与容积法相结合用于计算层状地基上桩基础阻抗函数的计算公式，并通过半无限地基和层状地基中单桩和群桩阻抗函数的求解，证明了方法的适用性。但是由于混合数值法求解过程中涉及到格林函数的求逆，对于大规模群桩问题计算量非常大，还需要解决计算效率等问题。

(2) 利用黏弹性人工边界运用直接法也可作为求解桩基础动刚度的一种方法，但在复杂地基条件下还需要考虑网格尺寸、模型大小等问题。

[1]杜蓉,张建友,隋丽丽，等.桩基承载力的ANSYS有限元分析[J].水利与建筑工程学报，2010,8(4):213-215.

[2]张麒蛰,卓卫东,范立础.斜桩基础工作性状的研究进展[J].水利与建筑工程学报，2013,11(4):60-66.

[3]肖晓春,林皋,迟世春.桩-土-结构动力相互作用的分析模型与方法[J].世界地震工程，2002,18(4):123-130.

[4]杜建国,林皋,谢清粮.大坝-地基动力相互作用研究中的几个问题[J].水利与建筑工程学报，2008,6(3):1-4.

[5]NovakM,SharnoubyBE.Stiffnessconstantsofsinglepiles[J].JournalofGeotechnicalEngineering, 1983,109(7):961-974.

[6]KayniaAM,KauselE.Dynamicsofpilesandpilegroupsinlayeredsoilmedia[J].SoilDynamics&EarthquakeEngineering, 1991,10(8):386-401.

[7]GazetasG,MakrisN.Dynamicpile-soil-pileinteraction.PartI:Analysisofaxialvibration[J].EarthquakeEngineering&StructuralDynamics, 1991,20(2):115-132.

[8]MakrisN,GazetasG.Dynamicpile-soil-pileinteraction.PartII:Lateralandseismicresponse[J].EarthquakeEngineering&StructuralDynamics, 1992,21(2):145-162.

[9]蒯行成,沈蒲生.层状介质中群桩竖向和摇摆动力阻抗的简化计算方法[J].土木工程学报，1999,32(5):62-70.

[10]蒯行成,沈蒲生.层状介质中群桩水平动力阻抗的简化计算方法[J].振动工程学报，1998,32(3):258-264.

[11]蒋通,程昌熟.用二次形函数薄层法分析弹性层状地基中的动力问题[J].力学季刊，2006,27(3):495-504.

[12]林皋,韩泽军,李建波.层状地基任意形状刚性基础动力响应求解[J].力学学报，2012,44(6):1016-1027.

[13]ZhongWX,LinJH,GaoQ.Theprecisecomputationforwavepropagationinstratifiedmaterials[J].InternationalJournalforNumericalMethodsinEngineering, 2004,60(1):11-25.

[14]韩泽军.基础与复杂层状地基动力相互作用研究[D].大连：大连理工大学,2014:22-28.

[15]刘晶波,吕彦东.结构—地基动力相互作用问题分析的一种直接方法[J].土木工程学报，1998,31(3):55-64.

[16]刘晶波,王振宇,杜修力，等.波动问题中的三维时域粘弹性人工边界[J].工程力学，2005,22(6):46-51.

[17]MiuraK,KayniaAM,MasudaK,etal.Dynamicbehaviourofpilefoundationsinhomogeneousandnon-homogeneousmedia[J].EarthquakeEngineering&StructuralDynamics, 1994,23(2):183-192.

[18]KayniaAM,KauselE.Dynamicsofpilesandpilegroupsinlayeredsoilmedia[J].SoilDynamics&EarthquakeEngineering, 1991,10(8):386-401.

[19]蒋通,田治见宏(日).地基-结构动力相互作用分析方法—薄层法原理及应用[M].上海：同济大学出版社,2009:267-268.

Methods of Dynamic Stiffness Computation for Pile Foundation

WANG Peng1,2, HAN Zejun3, HU Zhiqiang1,2

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China; 2.InstituteofEarthquakeEngineering,FacultyofInfrastructureEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China; 3.SchoolofCivilEngineeringandTransportation,SouthChinaUniversityofTechnology,Guangzhou,Guangdong510641,China)

With the expansion of the scale of modern engineering construction, pile foundation has been widely used. Focusing on this problem, this paper adopted two methods to compute the impedance functions of pile foundations, first is the substructure method, in which only the piles are discretized, and the hybrid numerical algorithm was used to solve the Green's functions for the layered foundation, and then the impedance function of pile foundations can be solved combining with the volume method. In the second method, the piles and the finite field soil around the piles were discretized and the impedance function can be obtained by applying the viscous-elastic artificial boundary on the boundaries. In the former method, the hybrid numerical algorithm have high accuracy and can be used to solve multi-layered soil. While in the latter method, the visco-elastic artificial boundary is simple and can be applied in large pile group system. In the numerical examples, the impedance function of single pile, 2×2 piles and 4×4 piles in semi-infinite foundation and piles foundation with pile cap in layered foundation were calculated to validate the accuracy of the two methods, and the effect of mesh size, selection of calculation range on the accuracy were also discussed. The results have certain guiding significance for the design and construction of piles.

dynamic interaction; group piles foundation; impedance function; hybrid numerical algorithm; viscous-elastic artificial boundary

10.3969/j.issn.1672-1144.2016.04.027

2016-03-27

2016-04-18

国家自然科学基金重点项目(51138001)