桥梁桩基极限承载力预测方法比较

罗红星，王兴国，宋　帅

(1.云南省公路开发投资有限责任公司， 云南 昆明 650200；2.云南省交通规划设计研究院， 云南 昆明 650011；3.中交第一公路勘察设计研究院有限公司， 陕西 西安 710075)



桥梁桩基极限承载力预测方法比较

罗红星1，王兴国2，宋帅3

(1.云南省公路开发投资有限责任公司， 云南 昆明 650200；2.云南省交通规划设计研究院， 云南 昆明 650011；3.中交第一公路勘察设计研究院有限公司， 陕西 西安 710075)

典型的桩基静载荷试验所测得的荷载-沉降曲线分为缓变型和陡降型两种，其极限承载力的确定方法也因此不同。对于不同形态的荷载-沉降曲线，由于试验条件限制而导致无法实测桩基极限承载力时，选择合理预测方法是获取极限承载力的快捷有效的方式。结合两种不同形态下桩基现场试验结果，分别采用折线法、双曲线法、百分率法、抛物线法及灰色理论等方法对现场试验桩基极限承载力进行预测。计算结果表明：双曲线法和抛物线法的预测误差较大，不宜采用；折线法和百分率法的预测误差在10%以内，精度较高；灰色GM(1,1)模型预测精度最高，其中修正的新陈代谢GM(1,1)模型的预测误差可达到1%。并通过现场试验中未达极限破坏的不完整荷载-沉降曲线进行预测，验证了新陈代谢GM(1,1)模型预测方法的合理性，具有一定的工程实用价值。

桩基工程；承载力预测；灰色理论；GM(1,1)模型

单桩极限承载力是设计基桩时主要考虑的控制性指标，确定单桩极限承载力有静载荷试验、动力测试、静力触探法和经验公式等多种方法，而静载试验法由于测试方法简便、试验结果直观可靠，成为比较常用的单桩极限承载力的确定方法之一。典型的单桩竖向静载荷破坏试验荷载-沉降曲线如图1所示，可分为陡降型和缓变型两种，陡降型Q-S曲线属于持力层突然失去承载力破坏，曲线上有明显的破坏特征点，Qf代表破坏荷载，实际取陡降起点Qu对应荷载作为其极限承载力。而缓变型Q-S曲线属于“渐进型”破坏，没有明显的破坏特征点，加载过程中沉降变化稳定，常由规范规定容许沉降Su来确定对应荷载Qu′作为单桩极限承载力。

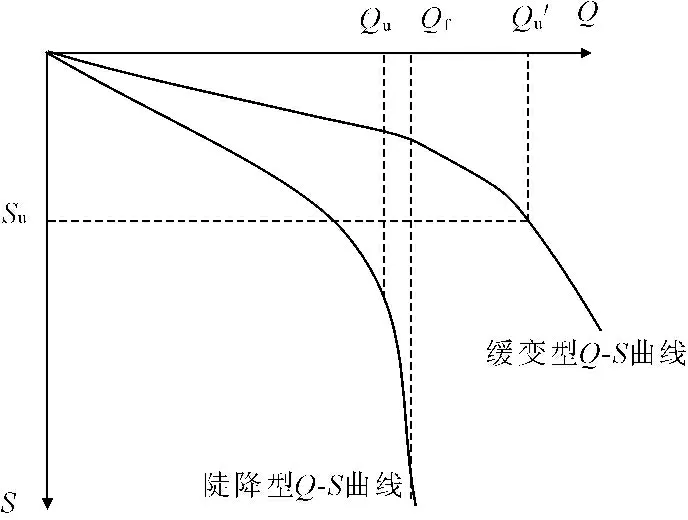
图1两种主要Q-S曲线

然而在现场试验中，由于荷载设备、试验费用、工程施工进度以及现场条件等限制，有时不能将试桩加载至破坏荷载，因此所得的试验数据是不完整的，无法得出其完整的Q-S曲线，所以不能直接得到单桩极限承载力。这种情况下，如何通过已测得的数据，简便快捷预测试桩的极限承载力具有重要意义[1-5]。

对此，国内学者做了大量研究工作,提出了多种理论计算方法。邓友生等[6]采用Mindlin解推导群桩沉降计算公式，计算了群桩作用下桩顶的沉降，并与试验值比较，验证了方法的可靠性，但该方法对于单桩却不能适用；高笑娟等[7]根据现场试验数据，采用双曲线法预测了挤扩支盘桩的承载力，得出了与实测曲线比较符合的结果，但该方法预测结果普遍偏大；赵春风等[8]运用完整的指数函数模型拟合了单桩荷载-沉降曲线，拟合结果较为精确，是一种可行的预测方法，但依然存在很多局限性；罗建华等[9]用灰色理论的预测方法，根据不完全的静载试验数据，预测了单桩极限承载力，并与高应变动力检测试验结果进行对比，误差较小，但在建立灰色模型预测极限承载力时，没有考虑到两种不同Q-S曲线形态确定极限承载力的方法是不同的，该方法需进一步深化。

本文在前人研究的基础上，搜集并整理了黄土地区典型的摩擦桩基静载试验数据，综合考虑不同形态Q-S曲线承载力计算方法，采用不同方法对单桩极限承载力进行了预测，预测结果进行对比，以期提出适用于摩擦桩基单桩极限承载力的预测方法。

1　现场试验

1.1缓变型Q-S曲线

试验数据选用陇汉线陕甘界至宝鸡高速公路五里坡特大桥试桩试验报告，现场地层以黄土为主，静载试验共设试桩四根，均采用机械旋挖钻成孔后灌注成桩，试桩桩径均为1.4 m、桩长均为40 m，分别记为S1、S2、S3和S4。其中S1试桩试验数据绘制Q-S曲线及S-lgt曲线见图2和图3，由图2、图3可知该曲线符合缓变型曲线特征。

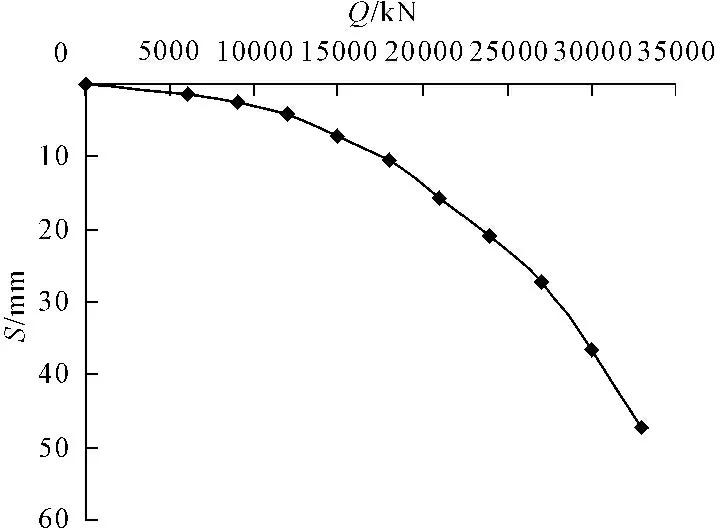
图2五里坡特大桥S1试桩Q-S曲线

由Q-S曲线及S-lgt曲线可知，加载至33 000 kN时试桩总沉降增大到40 mm以上，取曲线图上沉降值为40 mm时对应荷载作为试桩的极限承载力，在Excel中通过曲线拟合得到S1试桩极限承载力为30 970 kN。

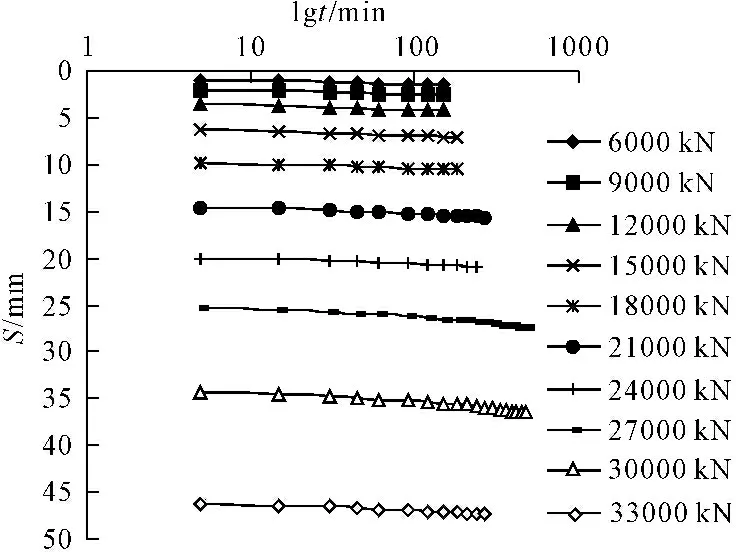
图3五里坡特大桥S1试桩S-lgt曲线

1.2陡降型Q-S曲线

选取陇汉线陕甘界至宝鸡高速公路五里坡特大桥试桩试验报告中更为典型的S4试桩试验数据绘制Q-S曲线及S-lgt曲线如图4和图5所示，由图4、图5可知该曲线符合陡降型曲线特征。

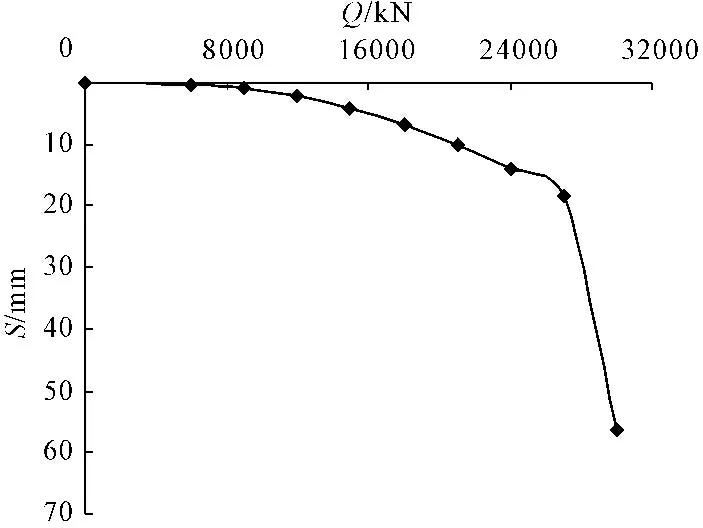
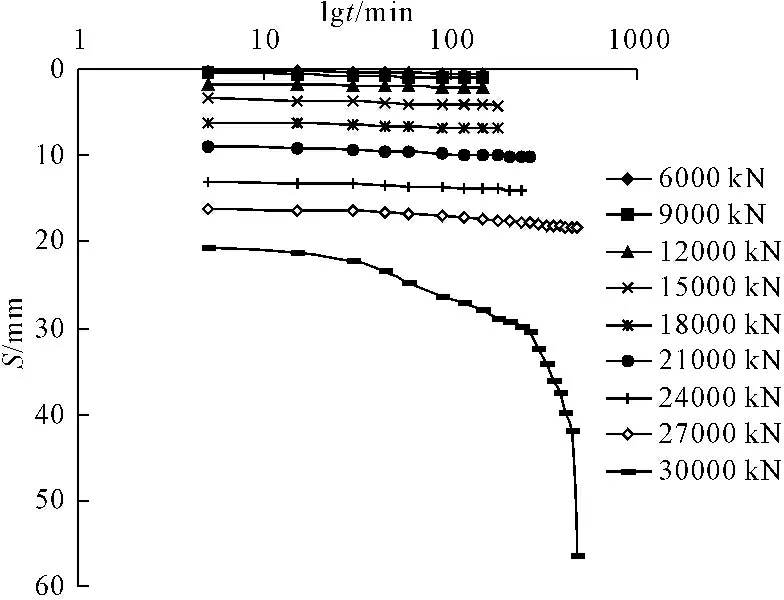
图4　五里坡特大桥S4试桩Q-S曲线

图5五里坡特大桥S4试桩S-lgt曲线

由Q-S曲线及S-lgt曲线可知，加载至30 000 kN时试桩总沉降迅速增大到56.47 mm，曲线上出现明显的转折点，认为此时试桩已达到破坏。取曲线图上陡降点对应荷载作为试桩的极限承载力，S4试桩极限承载力为27 000 kN。

1.3未达到极限破坏荷载的Q-S曲线

试验数据选用黄延高速扩能工程LJ-4标段冯家河大桥进行单桩竖向静载试验，现场地层以黄土为主，试桩桩径均为1.5 m、桩长均为30 m，加载至18 000 kN时由于反力梁无法继续维持加载而终止，试桩实测荷载沉降数据绘制Q-S曲线及S-lgt曲线见图6和图7。

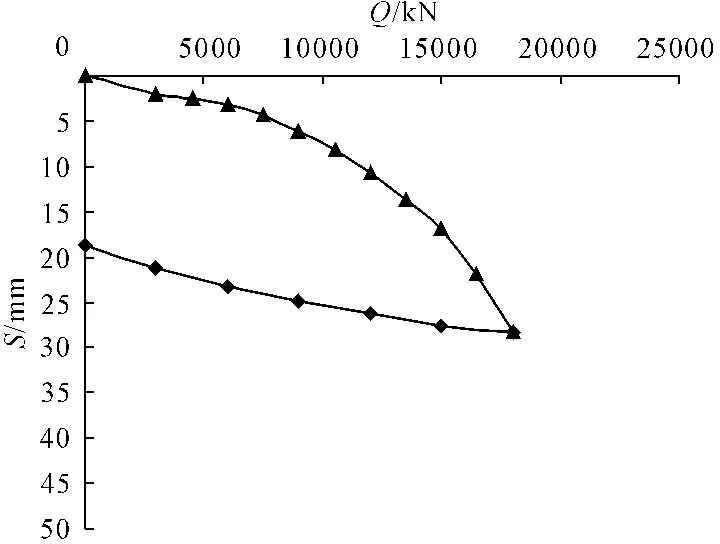
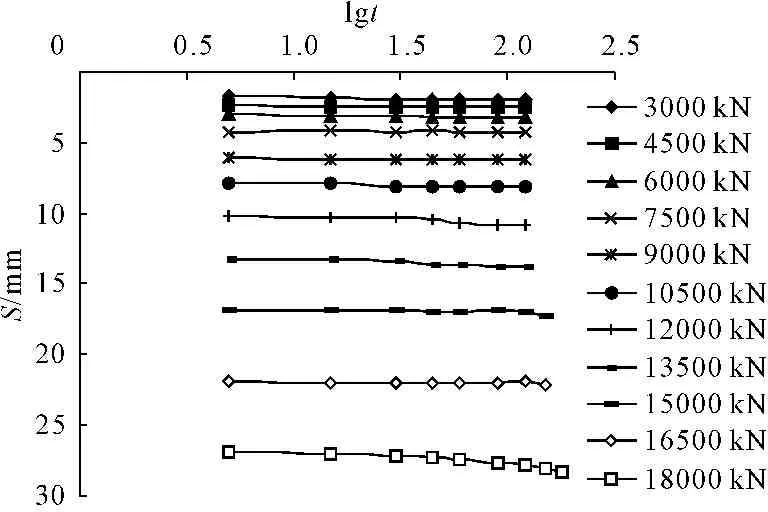
图6　冯家河大桥试桩Q-S曲线

图7冯家河大桥试桩S-lgt曲线

从图6、图7可以看出，试桩最大沉降量为28.34 mm，卸载完成后最大回弹量为9.63 mm，回弹率为33.96%，试桩没有达到破坏，桩周土体还未完全发挥其承载能力，因此试桩极限承载力大于18 000 kN。需要选用合理的承载力预测方法，根据已有的部分数据，对其极限承载力进行预测。

2　灰色GM(1,1)模型

广义非等步GM(1,1)模型[10]为：

(1)

上述微分方程还可表示为:

(2)

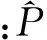
(1) 残差检验

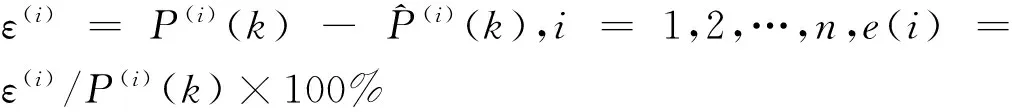
(2) 后验差检验

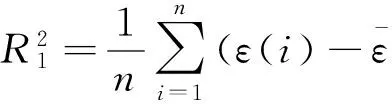
根据后验差比值C和小误差概率T两个指标可综合评定预测精度，当各指标满足表1要求时，满足预测精度即可按式(1)和式(2)进行预测。

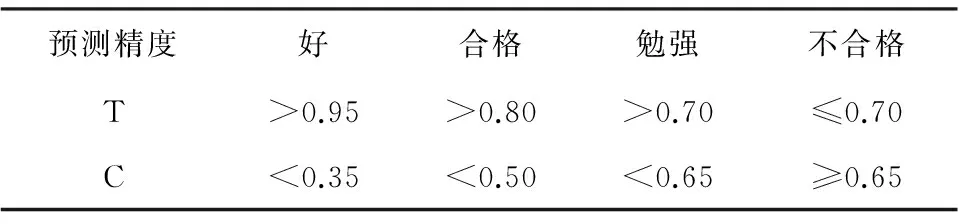
表1　预测精度

当广义GM(1,1)模型预测精度不满足要求时，考虑对原模型进行残差修正来提高模型的预测精度，步骤如下[12]：

ε(1)={ε(1)(1),ε(1)(2),…,ε(1)(n)}，其中

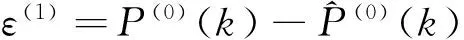
按照上述建模方式有：

(3)

则其还原模型为：

(4)

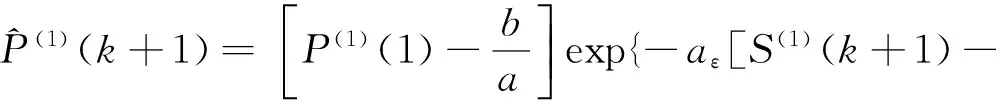
(5)

当式(5)中S(1)(k+1)趋近无穷时，单桩极限承载力预测值为[14]:

(6)

Q-S曲线随着荷载等级增加而不断延展，在模型中补充新荷载数据P(1)(n+1)和对应的沉降数据S(1)(n+1)并按照补充新信息之后的全数列建模得到的预测模型称之为新信息非等步模型。其极限承载力预测值同式(2)。

随着灰色系统发展[15]，随机扰动因素进入系统使得老数据的意义减弱，去掉根本不可能反映系统目前特征的初始数据，补充预测得到的新信息更能体现系统现时特征，这种具有新陈代谢性质的GM(1,1)模型是最理想的预测模型。将原始数据序列去掉P(1)(1)、S(1)(1)，并补充新数据P(1)(n+1),S(1)(n+1)则有：

P(1)={P(1)(i)|i=2,3,…,n+1}

(7)

S(1)={S(1)(i)|i=2,3,…,n+1}

(8)

根据式(7)和式(8)生成序列建立预测响应函数，检验预测精度满足要求后继续往复上述过程，预测值大于广义GM(1,1)模型初始预测值则停止，此时建立的预测函数模型即为新陈代谢GM(1,1)。

3　预测结果精度分析

3.1缓变型Q-S曲线单桩极限承载力预测

取S1试桩试验数据后五组荷载沉降数据采用不同方法进行预测: Q分别为18000kN、21000kN、24000kN、27000kN、30000kN；S分别为10.51mm、15.59mm、20.85mm、27.38mm、36.47mm。

3.1.1折线法

对五组数据建立线性回归方程，求得相关系数a=1.763、b=2.3028×10-4，R2=0.995即Si=1.763exp(2.3028×10-4Qi)。按照ΔQ=3 000kN每级荷载递增量带入拟合指数曲线公式，可以算出加载至Qi+1时对应沉降量Si+1，计算Ki、(ΔK/ΔQ)及(Δ2K/ΔQ2)见表2，绘制Q-(Δ2K/ΔQ2)折线图如图8。

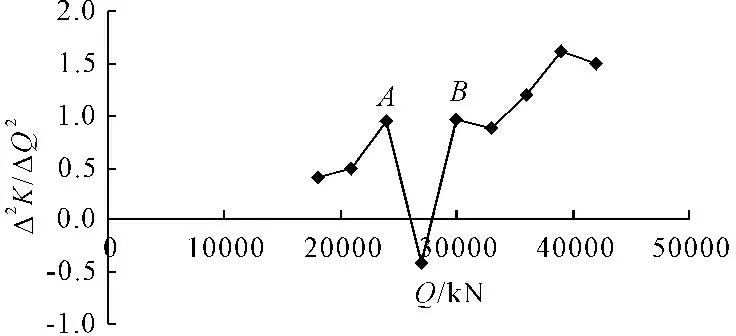
图8Q-Δ2K/ΔQ2折线

图8中折点A的荷载值QA=24 000 kN对应的是Q-S曲线上的屈服荷载Qy，B点荷载值可认为接近极限承载力Qu，Qu=Qy/0.765，算得Qu=31372.55 kN。

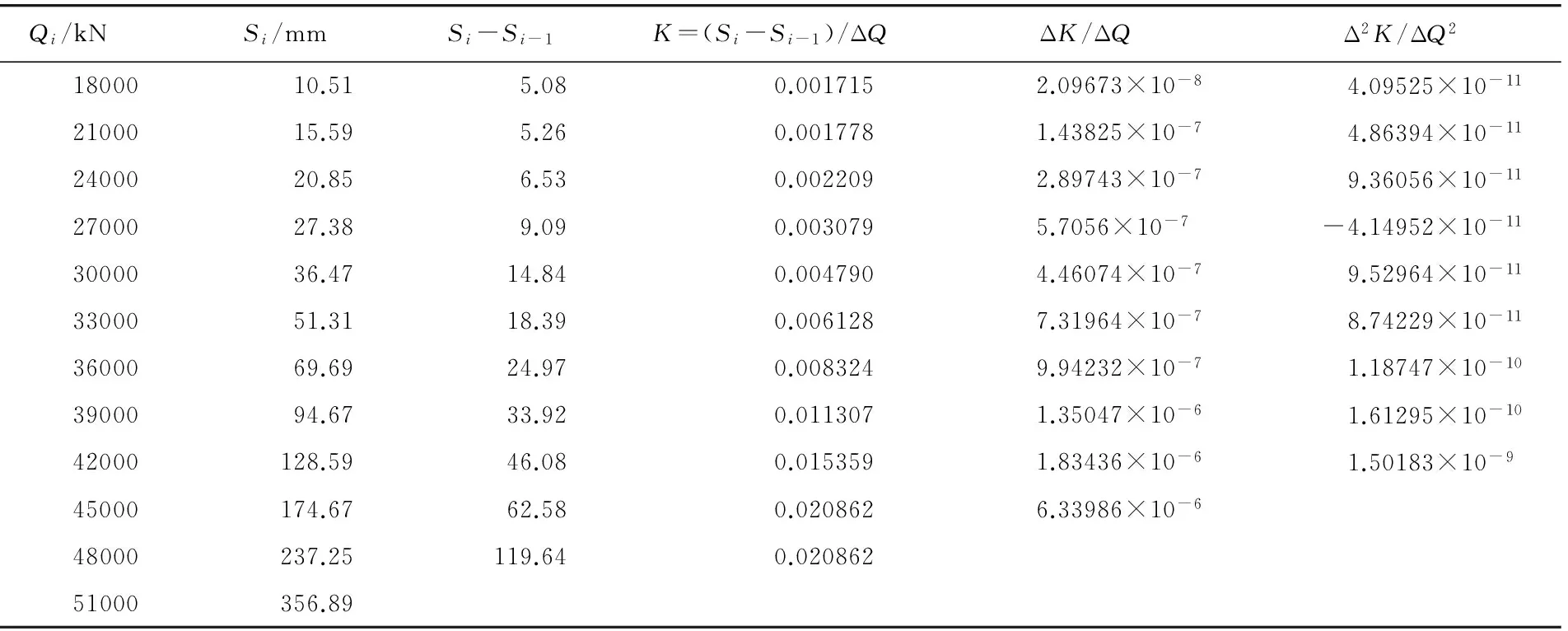
表2　Δ2K/ΔQ2计算结果

3.1.2双曲线法

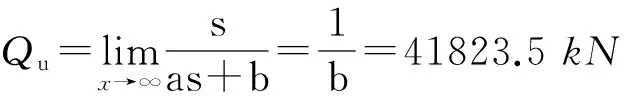
3.1.3百分率法

假定Q-S曲线符合指数方程Q=Qu[1-exp(-αS)]，变化为线性方程形式为S=a+bln(1-Q/Qu)，已知数据之后的Q-S数据，可根据折线法中确定的指数函数分别假定不同的Qu值结合已知实测值建立线性回归方程，当相关系数|R|接近1时表明线性相关程度最高对应Qu即为所求极限承载力。

计算中取解得相关系数近似为1时的Qu。分别假定Qu=30000kN、33000kN、36000kN，计算结果如图9所示，从图9中可以看出，假定极限承载力Qu=33000kN时相关程度最高。

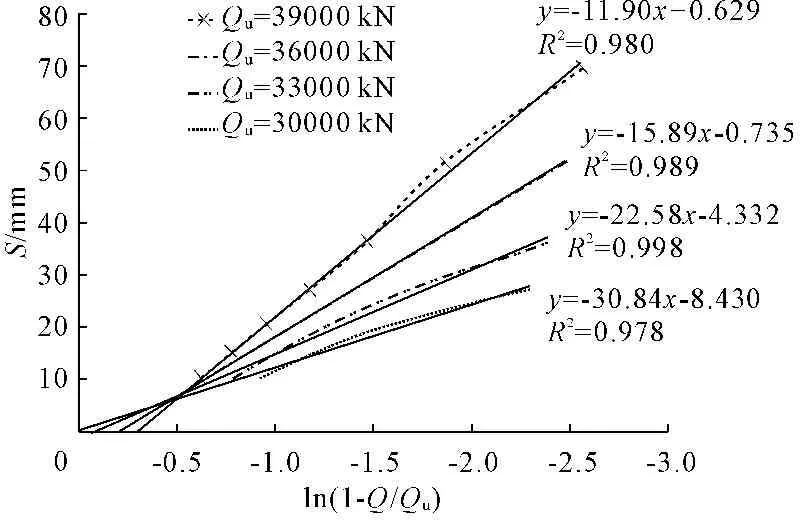
图9百分率法线性方程

3.1.4抛物线法

任选一组等值桩顶沉降量水平线，如图10所示，选择每5 mm为一档，根据其与Q-S曲线交点作对应荷载竖直线，从它与横轴交点作与横轴成45°斜线与之后每一荷载竖直线相交求得一组交点，对这组交点线性拟合后得到相应的直线与荷载横轴的交点即为极限荷载，得到Qu=34750 kN。

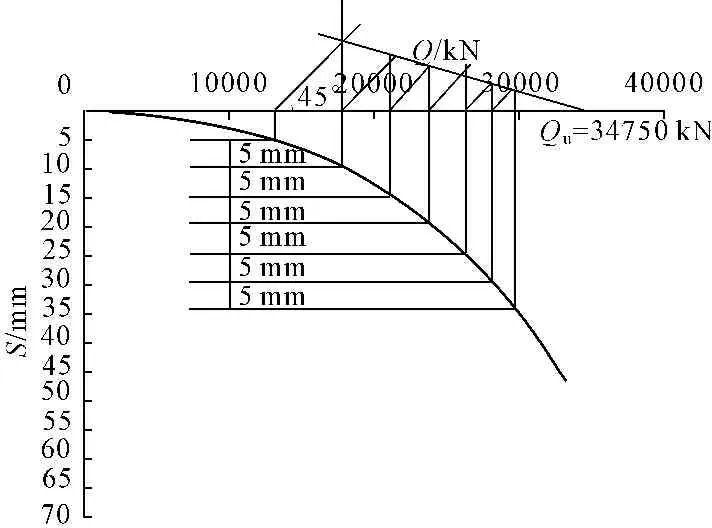
图10抛物线法

3.1.5新信息GM(1,1)预测

运用MATLAB进行矩阵计算得到：

即发展系数a和灰作用量b分别为0.032691和1269.8。新信息GM(1,1)预测单桩极限承载力值Pyc=30 894 kN，预测误差为0.24%，后验差比值R2=0.1456。检验小误差

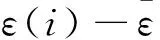
得到小误差概率T=1，预测精度满足要求。

3.1.6新陈代谢GM(1,1)预测

建立新陈代谢GM(1,1)预测模型：保持模型维度不变，去掉初始荷载值和沉降值并补充第10级预测荷载及沉降数据。桩顶荷载新序列变为P(1)=[21000 24000 27000 30000 33000]，沉降序列变为S(1)=[15.59 20.85 27.38 36.47 49.05]。

运用运用MATLAB进行矩阵计算得到：

新陈代谢GM(1,1)预测单桩极限承载力Pyc=30 978 kN，预测误差为0.03%，检验预测精度满足要求。需要注意的是当检验新陈代谢GM(1,1)预测精度不满足表1要求时，可往复上述过程不断淘汰旧数据补充新数据建模，一般都能得到较好的预测结果(见图11)。

几种Q-S曲线预测结果对比见表3。

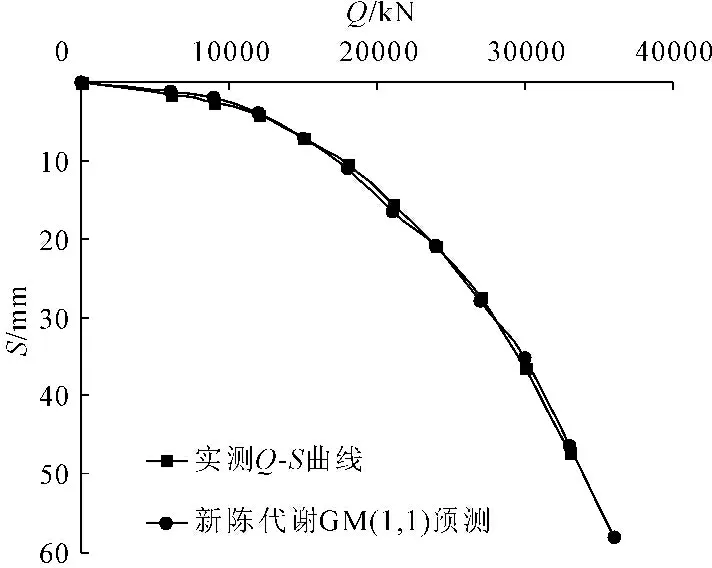
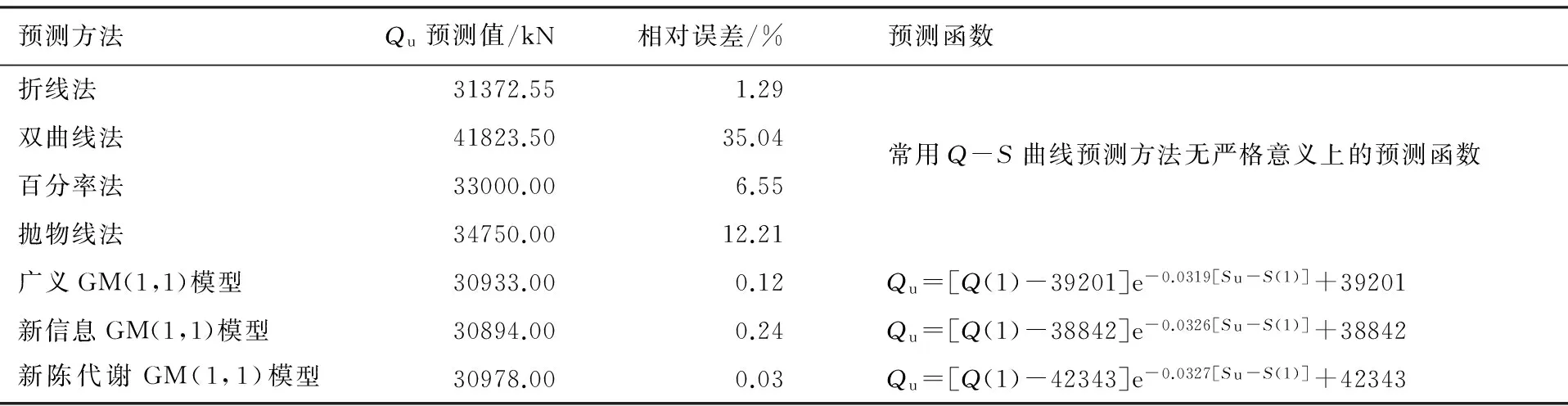
图11　试桩实测Q-S曲线与新陈

注：式中Q(1)、S(1)为选取数据序列首项值，Su为拟控制沉降量。

从表3和图11中对比结果可以看出，对于“缓变型”试桩极限承载力的预测，四种常用的Q-S预测方法中，双曲线法预测结果与实测值相差较大，这是由于双曲线法求得极限荷载值为沉降S趋于无穷时的荷载值，即为试桩的破坏荷载。抛物线法预测结果也偏大，不宜采用；百分率法和折线法预测结果较为精确，误差在10%以内。相比于常用的Q-S预测方法，灰色GM(1,1)模型预测精度最高，其中修正的新陈代谢GM(1,1)模型的预测误差可达到0.03%。采用灰色新陈代谢GM(1,1)模型预测“缓变型”试桩极限承载力，灰色预测模型建立的预测函数可以方便的实现根据沉降控制值确定极限承载力。

3.2陡降型Q-S曲线单桩极限承载力预测

选用S4试桩试验数据，其Q-S曲线符合陡降型曲线特点。选取不同数据序列采用灰色理论对Q-S曲线呈陡降型单桩极限承载力进行预测，分别建立不同预测步长的非等步GM(1,1)预测模型，运用MATLAB运算结果见表4、图12。

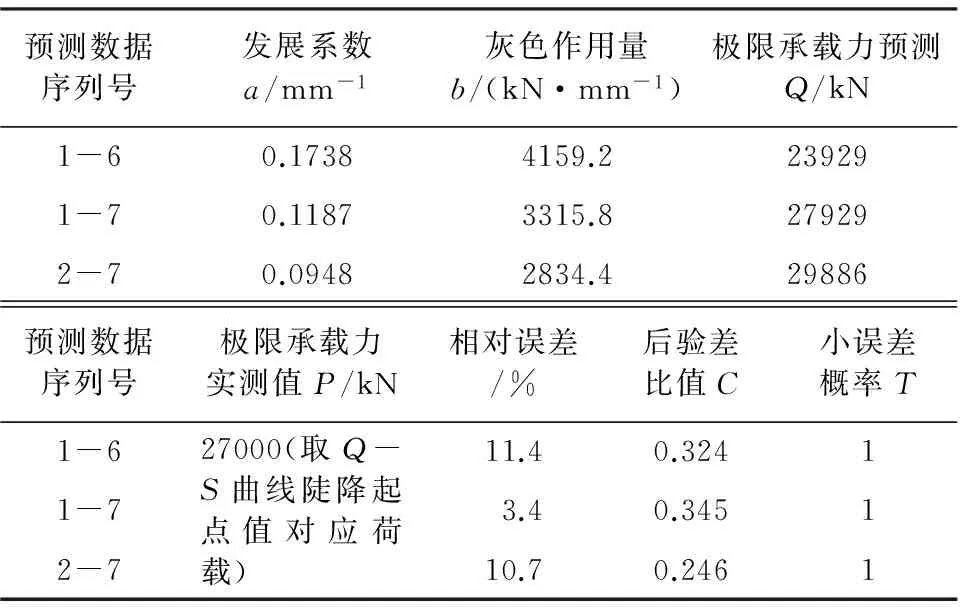
表4　S4试桩不同步长GM(1,1)预测结果

选取不同的原始荷载数据序列级数预测极限承载力发现：对于“陡降型”Q-S曲线，选取不同的数据序列进行灰色建模，预测误差离散性强，无明显规律。选取预测精度最高的数据序列，以试桩S4的1～7级荷载-沉降数据序列分别建立试桩的极限承载力预测的修正GM(1,1)模型群，对比模型各自预测精度结果见表5。

表5　S4试桩四种预测模型分析结果

从表5和图12中可以看出，对于Q-S曲线呈“陡降型”试桩，广义GM预测模型精度较低，相对误差在10%左右，修正的预测模型中新陈代谢GM(1,1)模型的预测结果精度最高，相对误差可控制在1%左右。

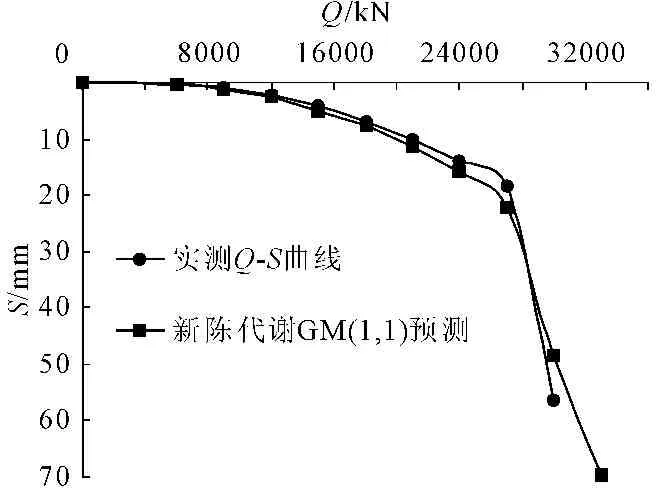
图12试桩实测Q-S曲线与新陈代谢GM(1,1)预测曲线

3.3未达极限破坏条件试桩承载力预测

选取黄延高速扩能工程LJ-4标段冯家河大桥静载试验数据，由于试验设备限制，未能达到其破坏荷载，现对其极限承载力进行预测。

依据以上结论，运用几种修正的灰色预测模型对已有静载试验数据进行预测可以得到很高的精度，且无论Q-S曲线呈“缓变型”或是“陡降型”，新陈代谢GM(1,1)模型预测精度最高。

初步分析上述静载试验结果，试桩Q-S曲线发展趋势未知，依据已有研究成果[10]，选取不同步长荷载-沉降数据序列建立灰色模型，对预测结果影响很大，选取合理的数据序列，则可以得到较为精确的预测结果。分别选取不同步长的已有荷载沉降-序列进行灰色建模计算，每级预测值与实测值的相对误差见图13。

从图13中可知，选取6-11级数据序列进行预测每级荷载预测值与已有实测值的相对误差最小。

选取6-11级荷载-沉降数据建立新陈代谢GM(1,1)模型，根据预测数据得到预测的Q-S曲线见图14，从图14中可以看出预测曲线前半段与实测曲线有一定差异，后半段与实测曲线拟合较好趋于重合，桩顶沉降为40 mm时预测曲线对应荷载值为19 756 kN，即预测极限荷载值为19 756 kN。

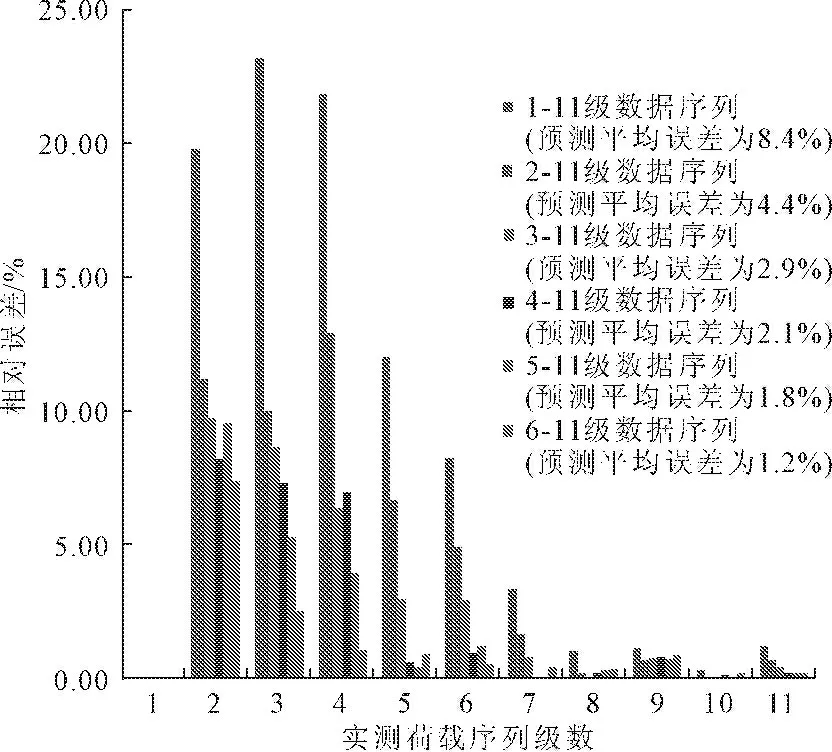
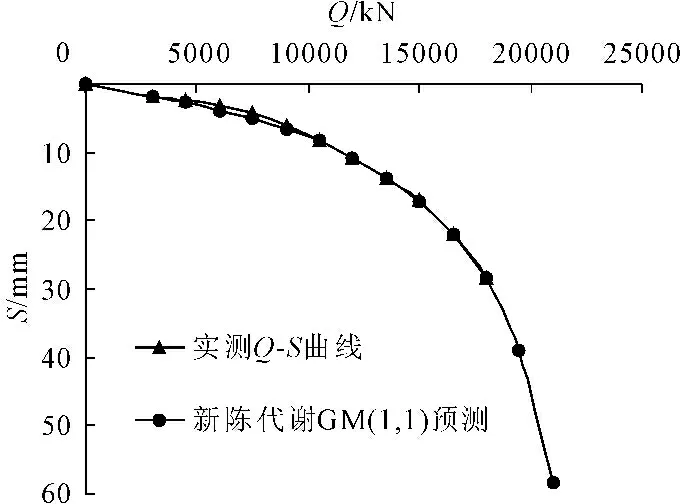
图13　不同级数数据序列得到每级荷载预测值与实测值相对误差

图14试桩实测Q-S曲线与新陈代谢GM(1,1)预测曲线

4　结　论

(1) 根据Q-S曲线呈“缓变型”试桩实测数据验证常用Q-S曲线预测方法中折线法概念清晰、预测精度高，预测相对误差可达1.29%，双曲线法预测相对误差较大，不宜采用；通过MATLAB编程实现各种GM(1,1)预测模型运算并结合多个工程实例证明灰色理论预测具有最高的预测精度，新陈代谢GM(1,1)模型预测相对误差可控制在1%以内。

(2)Q-S曲线呈“陡降型”单桩极限承载力灰色预测精度与选取静载试验的数据级数有密切关系，选取中长距离的数据序列预测可能造成较大的偏差，后几级荷载-沉降数据最能反映曲线后续变化趋势，且静载试验施加荷载越接近极限荷载，根据实测值建模得到的预测值精度越高。

(3) 对于两种常见Q-S曲线，新陈代谢GM(1,l)模型预测精度都是最高。增加反映系统现时特征的预测新数据才能不断接近单桩实际极限承载力。利用有限的试验数据选取预测相对误差最小的数据序列，运用新陈代谢GM(1,1)模型对静载试验的不完全Q-S曲线进行预测拟合,预测误差离散型小，得到的预测Q-S曲线能够为工程实际提供一定参考。

[1]邓志勇，陆培毅.几种单桩竖向极限承载力预测模型的对比分析[J].岩土力学,2002,23(4):428-431.

[2]戚科骏,徐美娟,宰金珉.单桩承载力的灰色预测方法[J].岩石力学与工程学报,2004,23(12):2069-2071.

[3]Ranian Satyamurthy, Mysore S Nataraj, Kenneth LMcmanis, et al. Investigations of pile foundationsin brownfields[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008(10):1469-1475.

[4]Lok T M H, Che W F. Axial capacity prediction fordriven piles using ANN: Model comparison[C]//Geotechnical Engineering for Transportation Projects. California,USA: ASCE, 2004.

[5]ZHAO J B, JIEWEN T U, SHI Y Q. An ANN model for predicting level ultimate bearing capacity of PHC pipe pile[C]// Earth and Space 2010: Engineering,Science, Construction, and Operations in Challenging Environments. [S.l.]: ASCE, 2010.

[6]邓友生，龚维明.基于Mindlin位移解的超大群桩基础沉降计算[J].武汉理工大学学报:交通科学与工程版,2008,32(3):420-422.

[7]高笑娟，朱向荣.用双曲线法预测挤扩支盘桩的极限承载力[J].岩土力学,2006,27(9):1596-1600.

[8]赵春风,李尚飞，等.完整指数函数拟合单桩荷载-沉降曲线的分析[J].同济大学学报(自然科学版)，2010,38(4):486-492.

[9]罗建阳，饶秋华.基于灰色系统理论单桩竖向极限承载力的预测[J].南华大学学报(自然科学版),2011,25(2):95-99.

[10]曹文贵，张永杰，赵明华.基桩极限承载力的改进变步长灰色预测模型研究[J].岩土力学，2006，22(S1)：774-778.

[11]王勇，蔡智，屈洋.CFG桩复合地基加筋褥垫层作用机理数值分析[J].水利与建筑工程学报，2016，14(1)：96-100.

[12]杨校辉，朱彦鹏，黄雪峰.静压桩荷载传递与承载性状试验研究[J].水利与建筑工程学报，2016，14(1)：139-143.

[13]苏航州，段伟，段晓伟.水平荷载作用下GRF桩基础受力特性的数值分析[J].水利与建筑工程学报，2015，13(3)：201-204.

[14]赵会永，张玉洁，钟涛.水平受荷桩的变形性能与承载力的灰色系统法预测[J].水利与建筑工程学报，2015，13(1)：114-120.

[15]崔雍，楚小刚，董嘉.基于神经网络的桩基竖向承载力预测研究[J].铁道工程学报，2016，211(4)：65-69.

Comparison Between Ultimate Bearing Capacity Prediction Methods of Pile foundation

LUO Hongxing1, WANG Xingguo2, SONG Shuai3

(1.YunnanHighwayDevelopment&InvestmentCo.,Ltd.,Kunming,Yunnan650200,China; 2.YunnanTransportPlanningandDesignResearchInstitute,Kunming,Yunnan650011,China；3.CCCCFirstHighwayConsultantsCo.,Ltd.,Xi’an,Shaanxi710075,China)

Typical pile foundation load test result curve can vary gradually and rapidly, thus its ultimate bearing capacity should be determined by different methods. For different load settlement behavior especially those whose bearing capacity cannot be tested directly because of limited condition, a proper prediction method can be a feasible and important way to determine its ultimate bearing capacity. This research choose two types of typical curves, which ultimate bearing capacity were determined by method of fold line, hyperbolic, percentage, parabola and grey theory. The results showed that the deviations of hyperbolic and parabola method are great; the deviations of fold line and percentage method are less than 10%; the accuracy of GM(1,1) method are highest of all, and the deviation of amended Metabolism GM(1,1) method nearly 1%. Then using the data of pile field load test below limited load to verify the consistency of Metabolism GM(1,1) method, and its results showed that GM(1,1) has some practical value in practical engineering.

pile foundation engineering; prediction of bearing capacity; grey theory; GM(1,1)

10.3969/j.issn.1672-1144.2016.04.026

2016-01-01

2016-02-20

交通部科技项目(2008353361420)

罗红星(1976—)，男，云南大理人，高级工程师，主要从事公路建设管理工作。 E-mail:jssxzhi@126.com

TU473.1

A

1672—1144(2016)04—0127—08