水位下降对复杂地基重力坝深层抗滑稳定分析——以武都水库重力坝19#坝段为例

刘 咏 梅

(湖南省水利水电职业技术学院， 湖南 长沙 410131)



水位下降对复杂地基重力坝深层抗滑稳定分析
——以武都水库重力坝19#坝段为例

刘 咏 梅

(湖南省水利水电职业技术学院， 湖南 长沙 410131)

武都重力坝基岩地质构造复杂，对坝体深层抗滑稳定极为不利。为了研究水位下降对武都重力坝抗滑稳定性的影响，以武都水库重力坝19#坝段为例，采用有限元法计算了坝体在库水位下降过程中的应力应变特性，重点研究坝基塑性破坏区的发展规律、坝体位移变化趋势以及坝体抗滑稳定性。结果表明：坝基塑性区主要分布在断层10f2两侧，随着上游水位的降低，塑性区的分布范围逐渐减小，重力坝和坝基发生逆时针方向的倾倒变形，坝顶最为明显；上游水位降低导致扬压力减小，坝体抗滑稳定系数增大，在死水位时稳定系数最大为3.0。说明随着库水位下降，重力坝抗滑稳定安全系数将逐渐增大。

抗滑稳定；有限元法；塑性区；安全系数

武都水库工程是武引二期的龙头骨干工程，位于四川省江油市武都镇上游4 km的涪江干流，主要建筑物有拦河大坝和坝后式厂房。拦河大坝为碾压混凝土重力坝，最大坝高120 m，坝顶长727 m，设计库容5.72亿m3，属国家大(Ⅰ)型水利工程，具有防洪、灌溉、生态供水、发电和旅游五大综合效益。

由于武都水库工程区位于龙门山褶断带前山构造带的北段，库尾和库首段分别有龙门山主中央断裂和前山断裂通过，且坝基岩溶洞穴、次级断层破碎带和层间错动带等软弱结构面发育[1]。因此，武都水库重力坝地质条件十分复杂，且坝体跨度很大，导致重力坝的抗滑稳定影响因素难以确定。

陈建叶等[2]以模型试验为基础，研究了武都碾压混凝土重力坝17#坝段坝基整体失稳的破坏过程、破坏形态和破坏机制，揭示影响坝基稳定的控制性因素，获得该坝段的滑动破坏机制与稳定系数；张艳红等[3]对武都重力坝混凝土进行弯拉强度和破坏过程的非线性分析，发现不同级配混凝土受初始静载、加载速率的影响不同；李桂林等[4]采用ANSYS软件对武都重力坝16#坝段、17#坝段剖面进行平面有限元分析，计算了库空和运行工况下16#坝段、17#坝段坝体与地基的安全系数分别为2.8和2.2。

已有的武都重力坝研究主要针对坝体滑动破坏机制与稳定性分析，而对于水位下降过程中坝基岩体塑性破坏区发展规律、坝体位移和坝基抗滑稳定系数的研究还很少。因此，本文以武都重力坝19#坝段为例，计算了库水位从校核洪水位开始下降的4种不同工况，旨在发现水位下降过程中重力坝底部基岩塑性破坏区的发展规律、坝体位移变化趋势以及坝体抗滑稳定性大小的变化规律，为大坝在各类运行工况下的稳定性评估提供参考。

1　抗滑稳定分析方法

目前，在重力坝设计中，计算不同运行工况的抗滑稳定系数是一项重要内容。工程上常采用传统的刚体极限平衡法进行计算，即通过计算各坝段不同水平截面上的外加荷载及应力，得出抗剪和抗剪断稳定安全系数。此法可用于地质条件较好及岩层走向规律的重力坝计算，但对于包含了大量节理裂隙等复杂结构面的基岩，极限平衡法计算量大增甚至无法计算[5-7]。

由于武都重力坝地基中分布有大量断层和错动带，极限平衡法无法考虑大量不利结构面。相比于传统刚体极限平衡法，有限元法可以同时建立多个结构面，还可以得到岩体的应力应变特征，更适合于地基复杂的重力坝深层抗滑稳定分析[8-11]。因此，本文选用有限元法计算武都水库重力坝的抗滑稳定，计算采用的材料模型为常用的摩尔-库伦模型[12-13]。

Zienkiewics O C等[14]在土工弹塑性分析中首次提出了强度折减法，此后广泛应用于各类岩土工程的稳定性分析。强度折减法是指将坝基岩体的真实抗剪强度(黏聚力和内摩擦角)除以一个折减系数F后再进行塑性计算，并以一定梯度逐渐增加F的大小，直到达到极限破坏状态为止，即塑性区贯通重力坝坝基滑裂面，认为此时坝体失稳，此时的折减系数即为重力坝的抗滑稳定系数[15-17]。其计算公式为：

(1)

(2)

式中：c和φ为折减前岩体的黏聚力和内摩擦角；c′和φ′为折减后的黏聚力和内摩擦角。

2　武都重力坝19#坝段模型建立

根据地质勘探测量报告得到了重力坝岩层走向及分布，发现基岩中存在较多的断层等不利结构面，对重力坝的深层抗滑稳定不利，鉴于目前对于19#坝段的研究较少，本文选用19#坝段进行建模。为了更精确的反映19#坝段的地质条件，构建模型时考虑了重力坝底部的4条主要断层，分别是F31、10f2、f115和f114。

最终重力坝19#坝段模型高110 m，基岩长500 m，宽180 m。模型建立后，网格划分时注意将坝体与坝基附近岩体网格进行加密处理，模型含1 505个单元，12 247个节点，具体见图1。

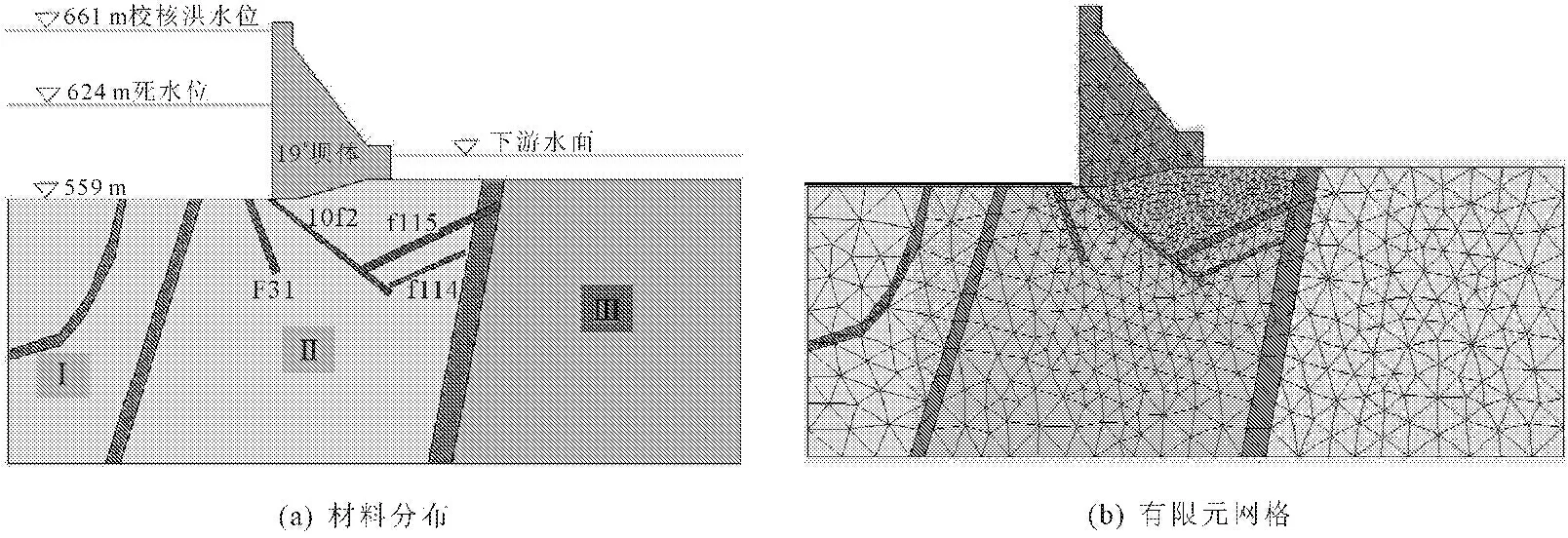
图1武都重力坝19#坝段模型

根据相关资料，选取了重力坝基岩岩体力学参数和坝体参数，其中断层组成物质为断层角砾岩、泥夹岩屑等，4条断层岩性相差不大，因此材料参数取相同值，如表1所示。

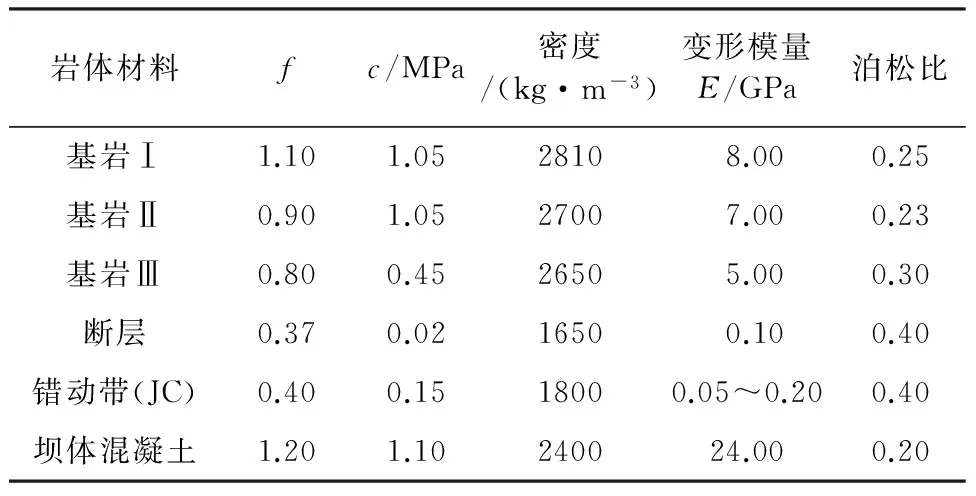
表1　重力坝19#坝段模型有限元力学参数

本文的计算流程是按照上游库水位从高程661 m(校核洪水位)开始，逐渐下降至658 m(正常蓄水位)、650 m和624 m(死水位)，分为共4个阶段，并标记为工况1～工况4，上游坝基高程559 m。相应的水位设置见表2。

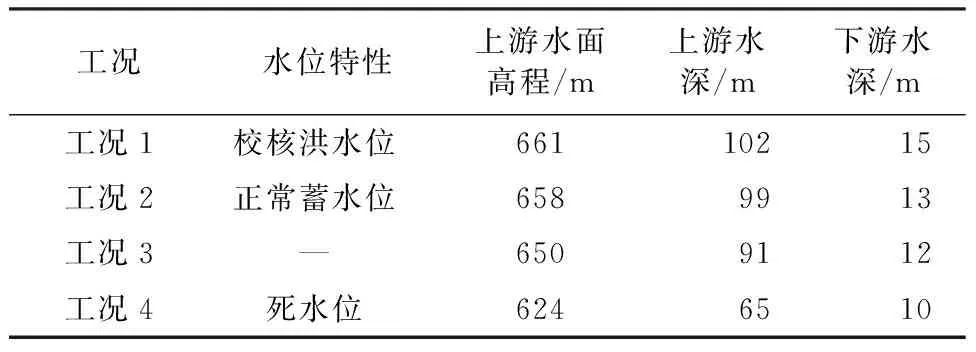
表2　相关计算工况设置

3　计算结果分析

3.1塑性破坏区分析

首先，根据表1中的参数进行有限元计算，得到了4种工况下不同水位时重力坝坝基的塑性破坏区，如图2所示。

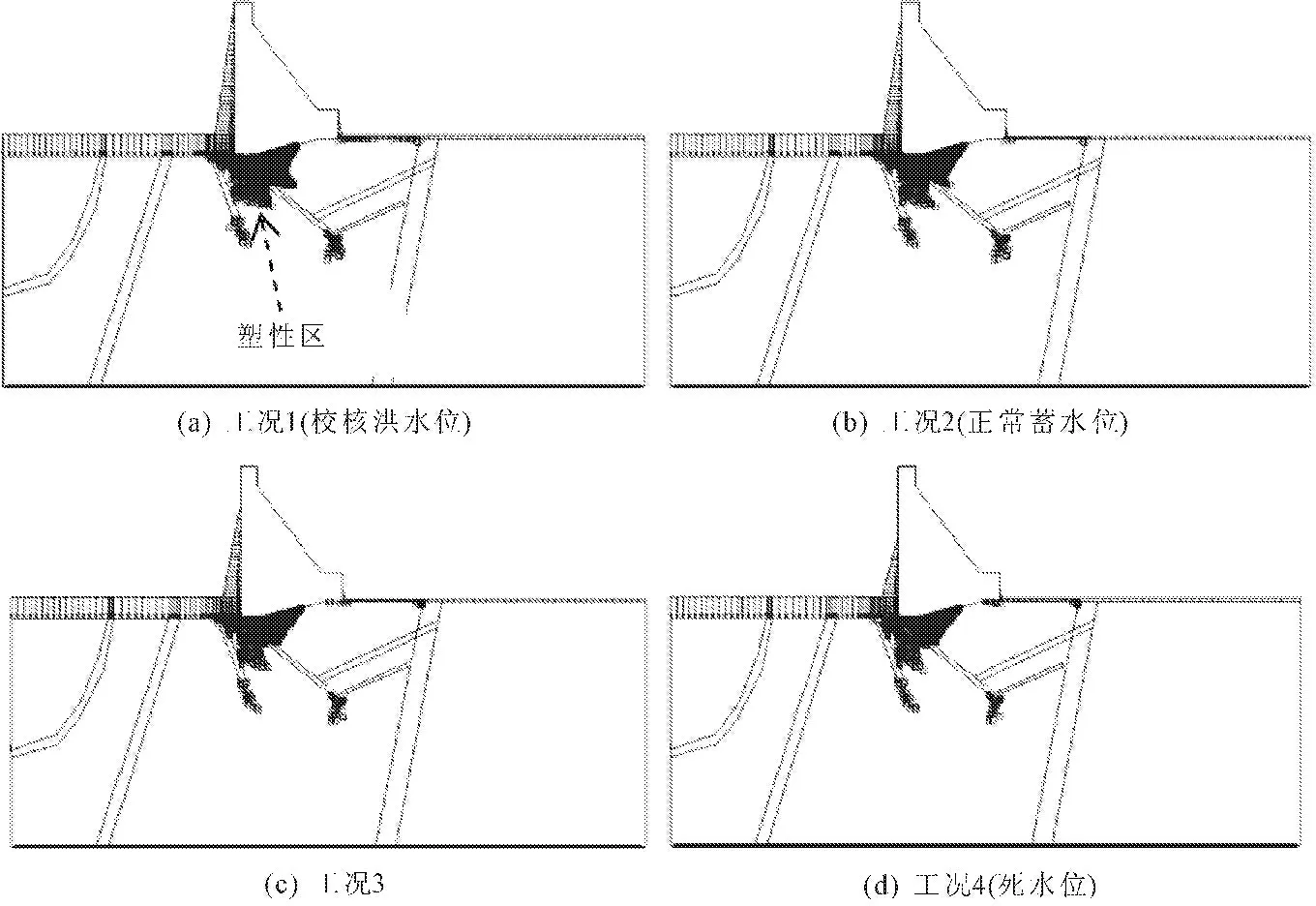
图2不同工况下重力坝基岩塑性破坏区分布

由图2可看出，4种工况下重力坝底部坝基的塑性区主要分布在断层10f2上部两侧，以工况1校核洪水位为例，见图2中(a)图，塑性区左侧与断层F31相连，右侧通过断层10f2并一直延伸到重力坝与基岩相交处，塑性点集中区右侧终止于坝体的中下底部位置，在下游坝基表层少量分布，而断层f115并未发生塑性破坏。根据以往资料显示，武都水库重力坝19#坝段的失稳模式是沿着断层10f2和f115深层滑动破坏的，虽然上游坝基断层10f2附近塑性区分布范围较广，但是并未与断层f115形成贯通，所以可认为坝体的抗滑稳定性良好。

此外，进一步分析4种工况下塑性区的发展趋势，发现随着上游水位的逐渐降低，塑性区的分布范围也逐渐缩小。主要体现在断层10f2两侧的塑性点明显减少，下游坝基表面的塑性点基本消失。说明水位下降有利于提高武都水库重力坝的坝基深层抗滑稳定性。

3.2大坝位移分析

本文研究的4种工况是从校核洪水位开始的，因此，在分析水位下降对坝体位移变化的影响前，应将初始时刻校核洪水位时坝体的位移做归零处理。最终，得到了库水位从校核洪水位下降后3种工况重力坝发生的水平位移，见图3。

由于篇幅限制，仅给出工况2和工况4水平方向位移云图，并规定水平位移向下游为正，向上游为负。分析可知，随着水位的下降，坝体将发生偏向上游的水平位移，且坝顶变形最大，越往下变形越小。上游水深从校核洪水位时的102 m下降至99 m后，坝体将发生向左的水平位移，最大值位于坝顶，约3 cm；当上游水深继续下降至65 m时(死水位)，坝顶水平位移约5 cm，坝体中部位移约2 cm～4 cm，坝体上游与坝基交界处(坝踵)发生局部变形，数值约1 cm～2 cm。

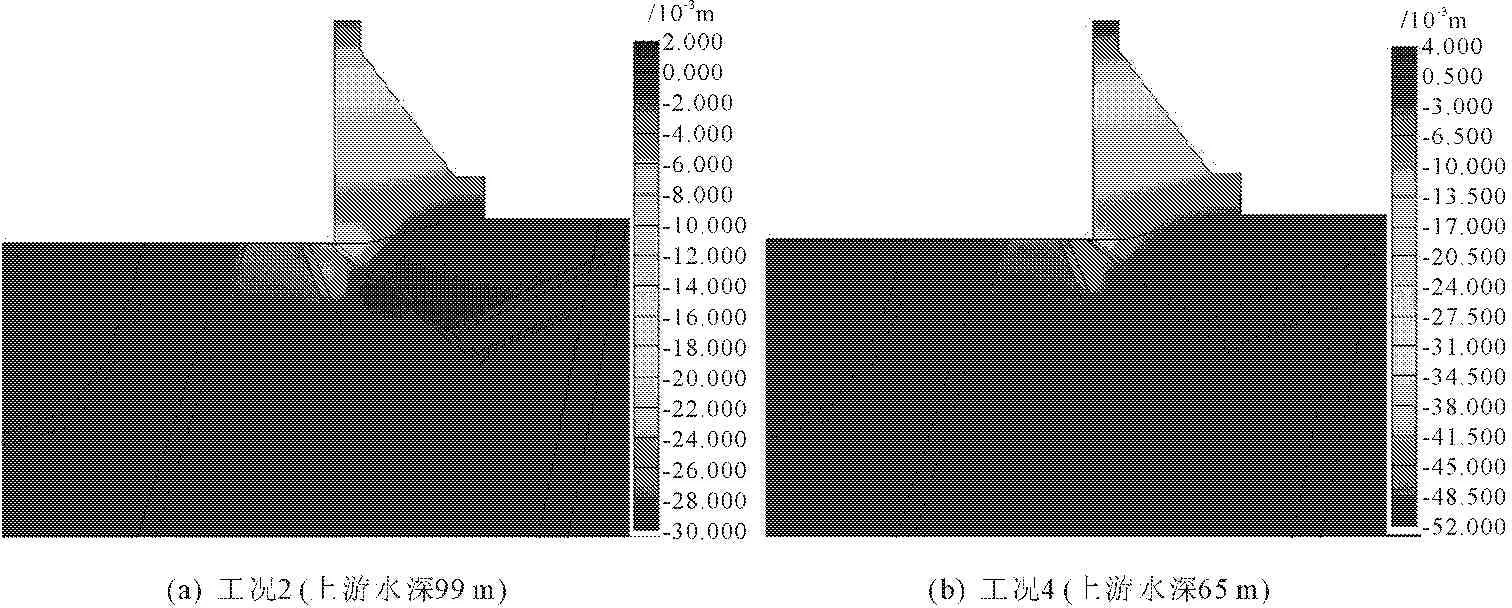
图3水位下降后重力坝发生的水平方向位移

图4为水位下降后重力坝发生的位移矢量，箭头方向代表坝体变形方向，箭头大小为位移大小。分析重力坝变形方向，发现水位下降后重力坝和坝基发生逆时针方向的倾倒变形，坝基变形集中在断层F31、10f2和f115附近。

图4水位下降后重力坝位移矢量

3.3抗滑稳定分析

重力坝的抗滑稳定安全系数可定量的反映大坝的安全程度，本文采用有限元强度折减法计算了4种水位工况下重力坝的抗滑稳定系数，计算结果见图5。

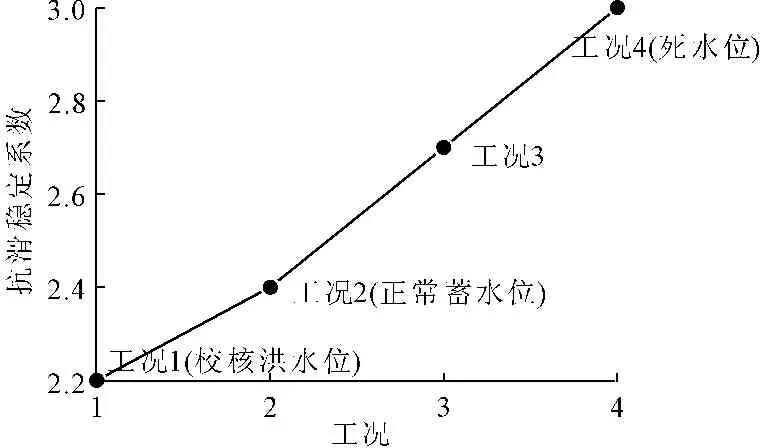
图5不同工况下重力坝抗滑稳定系数

在上游水位处于校核洪水位时，重力坝坝基抗滑稳定系数为2.2，当水位下降至正常蓄水位时增加到2.4，而在水位下降至死水位时稳定系数提高到3.0。分析原因，是由于随着重力坝坝前水位的下降，导致坝体所受垂直向上的扬压力有所减小，从而增大了重力坝作用在地基上的有效压力，最终提高了重力坝坝基的抗滑能力，所以随着坝前水位的下降，坝体抗滑稳定能力有增大的趋势，而在校核洪水位时稳定性最低。

4　结　论

本文以武都水库重力坝19#坝段为计算背景，研究了库水位下降过程中重力坝坝基塑性破坏区的发展规律、坝体位移变化趋势以及坝体抗滑稳定性大小，得到以下结论：

(1) 武都重力坝塑性区主要分布在坝基断层10f2两侧，且随着上游水位的降低，塑性区的分布范围逐渐减小，下游坝基表面的塑性点基本消失。水位下降对武都水库重力坝的坝基深层抗滑稳定有利。

(2) 随着上游水位的降低，重力坝和坝基发生逆时针方向的倾倒变形，降低至死水位时坝顶最大水平位移约5 cm，越往下变形越小，坝踵处发生局部变形，数值约1 cm～2 cm。

(3) 上游水位降低导致扬压力减小，坝体抗滑稳定系数增大，在校核洪水位时稳定系数最小为2.2，在死水位时最大为3.0。表明大坝在各种运行工况下均能保持自身的稳定。

[1]卢坤林,朱大勇.武都水库坝基深层抗滑稳定性评价中BD角的合理取值[J].水利水电科技进展,2012,32(3):35-38.

[2]陈建叶,张林,陈媛,等.武都碾压混凝土重力坝深层抗滑稳定破坏试验研究[J].岩石力学与工程学报,2007,26(10):2097-2103.

[3]张艳红,胡晓.武都重力坝碾压混凝土动态弯拉性能的试验研究与数值分析[J].水利学报,2011,42(10):1218-1225.

[4]李桂林.武都重力坝深层抗滑稳定模型试验和数值分析研究[D].成都：四川大学,2006.

[5]吴杰芳,张林让,陈震.混凝土重力坝深层抗震抗滑稳定分析研究[J].长江科学院院报,2010,27(6):58-61.

[6]厉丹丹,李同春,肖峰.龙滩大坝抗滑稳定可靠度分析[J].水电能源科学,2010,28(1):54-56.

[7]董建华,张林,杨宝全,等.复杂地基上重力坝深层抗滑稳定降强法试验研究[J].水利与建筑工程学报,2014,12(4):72-76.

[8]薛晓鹏,王维维,郑柯君.软基岩层上的混凝土重力坝设计及基础处理[J].水利与建筑工程学报,2015,13(3):140-144.

[9]张朝辉.基于强度折减法的复杂地基重力坝抗滑稳定分析[J].人民珠江,2015,36(3):73-76.

[10]聂彦春,王刚,马震岳,等.基于强度折减法的重力坝坝基软弱结构面失稳判据研究[J].水利与建筑工程学报,2013,11(4):13-16+37.

[11]王河,王志鹏,李永刚.基于有限元超载—折减综合法的重力坝深层抗滑稳定性分析[J].水电能源科学,2016,34(2):65-68.

[12]孙伟,庞俊蕊,苏龙,等.重力坝深层抗滑稳定强度折减弹塑性有限元法[J].人民黄河,2014,36(1):107-108.

[13]任青文,刘爽,陈俊鹏,等.基于损伤理论的重力坝坝基岩体渐进破坏数值模拟研究[J].水利学报,2014,45(1):1-9.

[14]Zienkiewics O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and Plasticity in soil mechanics[J]. Geotechnique, 1975,25(4):671-689.

[15]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-62.

[16]赵川,付成华,何欢,等.锦屏水电站缆机平台高陡边坡开挖支护数值模拟[J].长江科学院院报,2015,32(8):94-98.

[17]Drucker D C, Prager W. Soil mechanics and plastic analysis in limit design[J]. Quarterly of Applied Mathematics, 1952,10(2):157-165.

Deep Anti-sliding Stability Analysis of Gravity Dam Under Water Level Drawdown Condition: Case of Wudu 19#Dam

LIU Yongmei

(HunanTechnicalCollegeofWaterResourcesandHydropower,Changsha,Hunan410131,China)

Geological structure of the foundation of Wudu gravity dam is complex, which is extremely unfavorable to the stability of the dam. In order to analyze the influence of the water level drawdown to the stability of Wudu gravity dam, this paper taking Wudu Reservoir 19#dam as an example, and the finite element method was adopted to simulate the changing process of stress and strain characteristics under water level drawdown condition, with a special focus on the foundation of plastic failure zone development law, trend of dam displacement and dam anti slide stability of size. The results showed that the dam foundation of plastic zone were mainly distributed on both sides of the fault 10F2, with decrease of the upstream water level, plastic the distribution range decreased gradually, gravity dam and its foundation reversed clockwise toppling deformation, the crest was the most obvious; upper level reduced uplift pressure decreased with the increase of dam stability against sliding coefficient increases, stability coefficient was 3.0 in the dead water level. With the drawdown of reservoir water level, the safety factor of anti-sliding stability of gravity dam will be increased gradually.

anti-sliding stability; finite element method; plastic zone; safety factor

10.3969/j.issn.1672-1144.2016.04.025

2016-05-01

2016-06-03

城市实现生态化防洪治涝措施建设探索研究(湖南教育厅13C581)

刘咏梅(1971—)，女，湖南株洲人，硕士，副教授，高级工程师，主要从事水工建筑物的研究工作。E-mail:3214770673@qq.com

TV642.3

A

1672—1144(2016)04—0123—04