华丽高速公路华坪岸边坡稳定性的DDA模拟研究

严　飞，邓　琴

(1.云南省交通规划设计研究院， 云南 昆明 650041；2.陆地交通气象灾害防治技术国家工程实验室， 云南 昆明 650041；3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室， 湖北 武汉 430071)



华丽高速公路华坪岸边坡稳定性的DDA模拟研究

严飞1,2，邓琴3

(1.云南省交通规划设计研究院， 云南 昆明 650041；2.陆地交通气象灾害防治技术国家工程实验室， 云南 昆明 650041；3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室， 湖北 武汉 430071)

为了对华丽金安金沙江大桥华坪岸的边坡稳定性进行评价，并能够直观了解边坡变形及可能的破坏过程，采用非连续变形分析方法(DDA)结合强度折减法对华坪岸z1剖面进行模拟。在计算模型中利用真实节理和虚拟节理的概念充分考虑了已有的断层、软弱结构面的表征。研究结果表明：在自然状态下华坪岸边坡是稳定的；在强度参数降低的情形下，华坪岸边坡可能的破坏形式为牵引式破坏，即沿着t3凝灰岩夹层和坡体前缘卸荷带陡倾结构面滑动。

非连续变形分析(DDA)；边坡稳定性；强度折减法；边坡破坏过程

边坡是人工边坡和自然斜坡的统称。在水利水电工程、港口工程，桥梁工程、房屋建筑及深基坑工程都会遇到边坡稳定问题，分析边坡稳定性的方法主要由极限平衡法、有限元法、离散元法、非连续变形分析方法(DDA)[1]。其中以极限平衡法和有限元法最为常用，不过极限平衡法假定岩土体为刚体，不考虑土体变形和应力的关系，且无法分析边坡的破坏过程[2]；有限元法则可以分析岩土体的变形及应力[3]，且通过节理单元可处理少量的不连续面，但对于含大量的不连续面的岩土体问题则显得无能为力。离散元方法[4-5]克服了有限元在处理大量非连续面所存在的困难，同时可以自动识别出新的接触，可处理大位移、大转动的问题。正是由于离散元的这些优点，其在岩土工程领域获得了广泛的应用，例如董金海等[6]用UDEC对三峡库区软硬互层高切坡崩塌进行了研究取得了较好的效果；李世海等[7]基于三维离散元刚性块体模型研究三峡永久船闸开挖稳定性问题；雷远见等[8]将离散元和强度折减法结合研究了边坡稳定性问题；胡亚东等[9]利用3DEC程序对水电站边坡开挖后的位移变形特征进行了分析。不过该方法存在的问题是，需要采用很小的时间步长，计算耗时巨大。非连续变形分析方法[10-12]，便于对块体的大位移、大转动等进行模拟，可以自动识别新的接触，因此便于处理各种接触问题。除此以外，DDA基于最小势能原理，力学上非常严格，且其用开闭迭代进行接触处理，接触力计算较离散元更为严格准确。因此该方法很适合用来分析含有软弱夹层或者结构面控制的边坡稳定状况。本文就是采用DDA方法来对华坪岸的边坡稳定性进行分析。

1　华坪岸边坡工程地质条件

拟建金安金沙江大桥位于金沙江中游干流河段的五郎河支流至美河冲沟之间的7 km长的河道上。金安金沙江大桥主墩和锚墩分别置于金沙江两岸斜坡之上，如图1所示，是5个备选桥位的三维示意图。所处位置总体呈近SN向发育，河道较为顺直局部略微弯曲。河谷呈“V”型，为纵向单斜谷，两岸地形基本对称。因受地层产状和顺河向陡倾角结构面影响，两岸岸坡多形成阶梯状地形。华坪岸为顺向坡，总体坡度20°～30°，变化较小。岸坡腰部斜向的发育一系列连续的30 m～60 m高的陡坎，陡坎的坡度可达45°以上。出露地层主要为二叠系上统玄武岩组上段(P2β3)，出露基岩为致密玄武岩、杏仁状玄武岩、火山角砾熔岩夹等多层凝灰岩软弱夹层，且受后期构造错动影响岩体破碎，凝灰岩层间卸荷带局部存在泥化夹层。

华坪岸坡地层整体产状近SN，倾向西，倾角12°～30°。同时发育有与河道近于平行和正交的两组陡倾角节理。另外，有倾角较缓且有局部泥化的t3凝灰岩软弱夹层。出露的基岩为致密玄武岩、杏仁状玄武岩、火山角砾熔岩夹等多层凝灰岩软弱夹层，且受后期构造错动影响岩体破碎，凝灰岩层间局部存在泥化夹层，边坡稳定性可能主要受t3凝灰岩软弱夹层的控制。

华坪岸的崩塌堆积体主要集中发育于岸坡腰部的陡崖之下，其沿着向坡外缓倾的凝灰岩层面形成台阶状堆积，目前处于稳定状态。

上岸坡岩体以物理风化作用为主。强风化带厚度一般小于15 m，局部可达20 m～25 m；中风化带垂直深度为35 m～65 m。岸坡岩体卸荷现象明显，且浅表部位的岩体沿着陡倾节理张开，顺坡向分布的凝灰岩层或流面发生剪切破坏。正是由于岸坡岩体的结构松弛，加速了岩体的风化和岸坡的局部变形崩塌发生。

图1工程区三维展示图

2　DDA基本原理及边坡模型的建立

2.1DDA基本原理

非连续变形分析方法(DDA)是石根华博士[12]提出的一种专门处理含大量非连续面的岩体问题的数值分析方法。其以块体的形心位移(u,v)、块体绕形心的转动(r0)和块体应变(εx，εy，εxy)为基本未知量，基于最小势能原理，形成系统刚度方程并求解。

2.1.1块体内任意一点位移的表征

块体i内任意一点(x,y)的位移U=(u,v)T，用完全一阶近似的位移函数来表征：

U=TDi

(1)

其中：Di为块体i的位移矢量；T为位移变换矩阵：

Di=(x,y,r,εx,εy,εxy)

2.1.2系统刚度方程的建立

系统的总势能包括块体的应变能，初始应力的势能，外荷载作用下的势能，惯性力势能和黏聚力势能。由最小势能原理，当势能取最小值时系统达到平衡。

块体系统的总势能可写成：

(2)

KD=F

(3)

若系统由n个块体组成，则方程(3)可进一步写为：

(4)

式中，Kij(i,j=1,2,…n)为6×6的子矩阵，当i=j时，Kij只与块体i的材料属性有关，否则，Kij与块体i和j之间的相互作用情况有关；Di代表块体i的位移矢量；Fi代表作用于块体i上的荷载矢量[13]。结合边界条件和块体系统的运动学条件，即可对上述方程求解，获得各个块体的位移、变形及应力状态。

2.1.3块体系统的运动学条件

块体之间相互接触时，块体之间应该满足无拉伸和侵入很小的条件。当块体相互接触且有侵入发生时，需要采用较大刚度的弹簧施加于块体之间来限制块体的侵入。初始时，根据块体之间的相对位置找出所有可能的接触对，并根据接触类型施加接触弹簧。块体之间有角-角接触、角-边接触两种基本接触类型，而边-边接触可转化为两个角-边接触[14]。

对角-角接触，只需要施加一个法向弹簧，而角-边接触则需施加一个法向弹簧和一个切向弹簧，并在总刚度矩阵中的相应位置加入接触子矩阵，求解式(3)。如果块体间的接触力为拉力，则撤销法向弹簧和切向弹簧，并修改刚度矩阵，重新求解式(3)。这个过程称为开-闭迭代，基于开-闭迭代不断调整接触状态，直到不再有接触力为拉力的情形发生，便进入下一个时间步的计算，此时的接触状态为下一个时间步中接触的初始状态[13]。

2.2边坡模型的建立

选取华坪岸的z1剖面为例(如图1所示的z1方案)，来分析华坪岸边坡的稳定性。以已有的节理、软弱夹层、断层为界面将整个模型划分为一系列的三角形块体，其中真实的节理、软弱夹层、断层处的接触参数(真实节理)采用该处实际的材料参数，而其余部分的接触参数(虚拟节理[11])则采用高强度的参数，以便于表征完整岩石。整个计算模型的网格如图2所示。

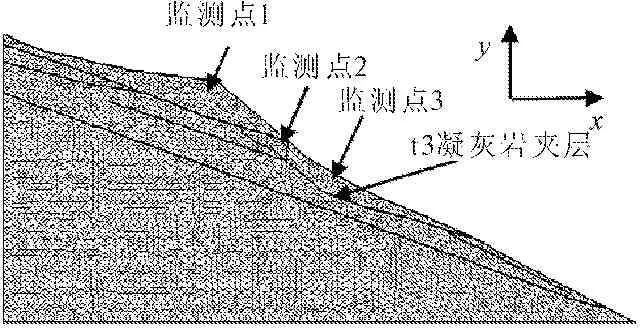
图2华坪岸z1剖面块体划分

研究该边坡在自然状态的稳定性及强度参数折减后的边坡破坏过程。为了便于了解边坡在不同折减系数下边坡的位移情况，我们在边坡的不同位置设置了3个监测点，如图2所示。

本文采用类似有限元中的强度折减法求稳定系数，即将节理面的强度参数c(黏聚力)和φ(内摩擦角)都除以折减系数K，得到一组新的强度参数值ck和φk，即：

(5)

然后用该组参数进行试算，直到边坡达到失稳临界状态，这时的折减系数K即为边坡的稳定系数。

2.3结构面参数

根据现场勘查及设计单位提供的勘察报告可知,该边坡可能会沿着t3凝灰岩夹层滑动。涉及到块体的滑动，因此结构面参数的选取就显得尤为关键。本次计算的参数根据基本岩石力学试验是及反分析综合确定，t3凝灰岩夹层的参数为c=24°，φ=50kPa，其余节理面的参数取为c=35°，φ=150kPa，重度取为29kN/m3。

3　模拟结果及分析

为了得到边坡在自然状态的稳定系数，采用不断增大的折减系数进行试算，看边坡的最终状态是否稳定。当折减系数K=1.4时，计算得到的边坡状态、位移矢量如图3所示。从图3中可以明显地看出，主要是t3凝灰岩夹层上方两个块体发生明显的滑动，最顶部的部分基本保持不动。由此，折减系数K=1.4时，边坡沿着t3凝灰岩夹层及坡体前缘卸荷带陡倾结构面出现明显的滑动，前缘部分先滑动，后缘部分失去支撑，也开始滑动，华坪岸边坡可能的破坏形式为牵引式破坏。这说明，华坪岸在自然状态的稳定系数约为1.4。

图4展示的是折减系数K=1.4时图2中的3个监测点的位移-时间步曲线。从图4中可知，监测点1的位移基本保持不变，说明监测点所在的块体是稳定的；监测点2、监测点3所在的块体恰位于t3凝灰岩夹层的上方，其位移不断增大，没有收敛的趋势。说明在该折减系数下，t3凝灰夹层上方的两个块体失稳，向下不断滑动，这说明在该折减系数下，华坪岸边坡失去稳定。

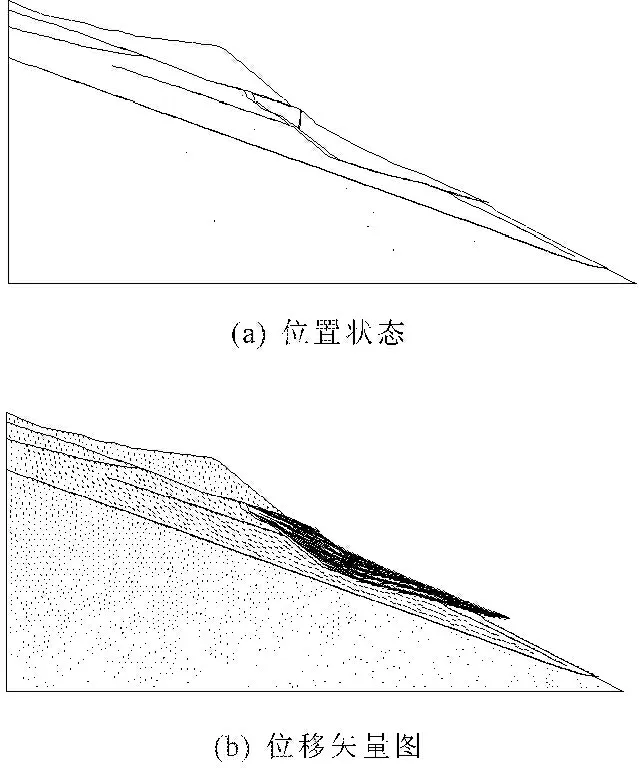
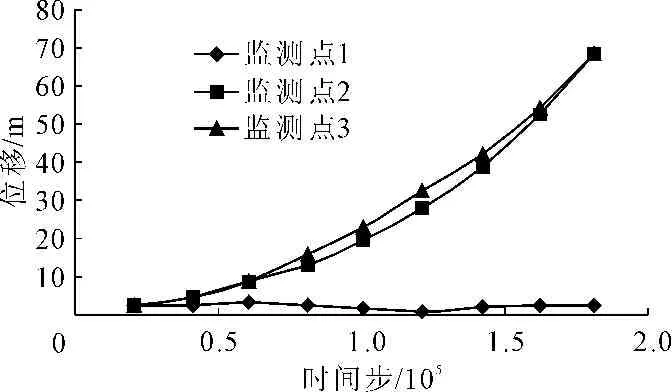
图3　折减系数K=1.4时华坪岸的位置状态

图4折减系数K=1.4时，监测点的位移时间步曲线

图5展示的折减系数K=1.3时3个监测点的位移时间步曲线。由图5可知，随着时间步的增大，3个监测点的位移均趋于稳定，并未出现图4所示的位移逐渐逐渐增大情况。

因此，在折减系数K=1.3时，边坡保持稳定状态。

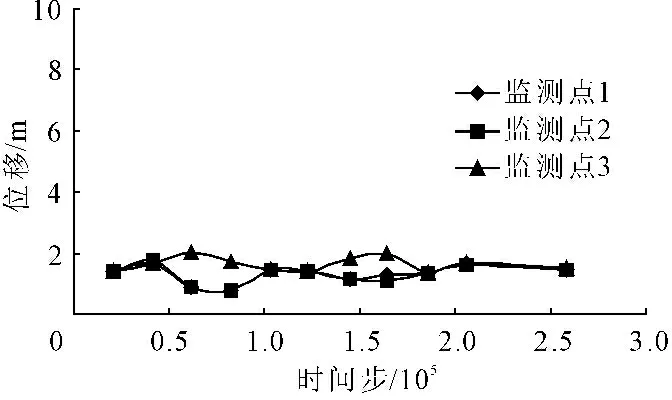
图5折减系数K=1.3时，监测点的位移时间步曲线

综合上述分析比较，可认为华坪岸的边坡稳定系数是1.4。

4　结　论

综合上面的分析可以得出如下结论：

(1)DDA中结合真实节理和虚拟节理的概念可充分考虑了已有的断层、软弱结构面的表征。结合强度折减法，DDA除可评价边坡的稳定性外，还可对边坡变形、破坏的全过程进行预测。

(2) 对华坪岸的模拟研究结果表明，在自然状态，华坪岸边坡是稳定的，在强度参数降低的情形下，华坪岸边坡可能的破坏形式为牵引式破坏，即沿着t3凝灰岩夹层和坡体前缘卸荷带陡倾结构面滑动。

致谢：感谢云交科2014(A)01—《金沙江中游库区高速公路大跨径桥址高边坡灾害调控技术及应用示范研究》项目的资助及课题组全体人员的配合、帮助和支持。

[1]方建瑞,朱合华,蔡永昌.边坡稳定性研究方法与进展[J].地下空间与工程学报,2007,3(2):343-349.

[2]FangJR,ZhuHH,CaiYC.Advancementandmethodsoftheslopestabilityresearch[J].ChineseJournalofUndergroundSpaceandEngineering, 2007,3(2):343-349.

[3]陈祖煜.土质边坡稳定分析:原理方法程序[M]．北京:中国水利水电出版社,2003．

[4]郑宏,李春光,李焯芬,等.求解稳定系数的有限元法[J].岩土工程学报,2002,24(5):626-628.

[5]CundallPA.Acomputermodelforsimulatingprogressivelargescalemovementinblockrocksystem[C]//SymposiumofInternationalSocietyofRockMechanics.Nancy:SymposiumISRM, 1971:129-136．

[6]ItascaConsultingGroupInc.UDECusermanualversion4.0[R]. [S.l]:ItascaConsultingGroupInc., 2004.

[7]董金玉,杨继红,伍法权,等.三峡库区软硬互层近水平地层高切坡崩塌研究[J].岩土力学,2010,31(1):151-157.

[8]DongJY,YangJH,WuFQ,etal.Researchoncollapseofhighcuttingslopewithhorizontalsoft-hardalternantstratainThreeGorgesreservoirarea[J].RockandSoilMechanics, 2010,31(1):151-157.

[9]李世海,高波,燕琳.三峡永久船闸高边坡开挖三维离散元数值模拟[J].岩土力学，2002，23(3)：272-277.

[10]雷远见,王水林.基于离散元的强度折减法分析岩质边坡稳定性[J].岩土力学,2006,27(10):1693-1698.

[11]胡亚东,肖燃,王剑梅.某水电站右坝肩倾倒变形边坡三维离散元数值分析[J].地质灾害与环境保护,2014,25(4):51-55.

[12]ShiGH.Discontinuousdeformationanalysis-anewnumericalmodelforthestaticsanddynamicsofblocksystem[D].Berkeley：UniversityofCalifornia-Berkeley, 1988.

[13]张秀丽．断续节理岩体破坏过程的数值分析方法研究[D].武汉：中国科学院武汉岩土力学研究所，2007．

[14]焦玉勇,张秀丽,刘泉声，等.用非连续变形分析方法模拟岩石裂纹扩展[J].岩石力学与工程学报,2007,26(4):682-691.

DDA Simulation of Huaping Shore Slope Stability of Huali Expressway

YAN Fei1,2， DENG Qin3

(1.EngineeringSurveyBranch,BroadvisionEngineeringConsultants,Kunming,Yunnan650041,China；2.NationalEngineeringLaboratoryforSurfaceTransportationMeterologicalHazardPreventionTechnology,Kunming,Yunnan650041,China； 3.StateKeyLaboratoryofGeomechanicsandGeotechnicalEngineering,InstituteofRockandSoilMechanics，ChineseAcademyofSciences，Wuhan,Hubei430071,China)

In order to evaluate the slope stability of Huaping shore of the Jinsha River Bridge, and intuitively understand the slope deformation and possible damage process, we use the discontinuous deformation analysis (DDA) method combined with strength reduction to simulate the slope of Huaping shore. Based on the engineering geological characteristics of Huaping shore, a calculation model of z1 profile was developed. In addition the concept of real joint and virtual joints joint was used, the faults or weak structure plane may take into consideration directly, the fracture of the rock itself also can be model naturally. The results show that: in the natural state, Huaping shore slope is stable. When the strength parameters reduced, Huaping shore slope is possible failure due to traction damage, the slope may slip along t3 tuff sandwich and steep joint, after that the small block behind the big block also began to slip because of loss support.

discontinuous deformation analysis (DDA); slope stability; strength reduction; slope failure

10.3969/j.issn.1672-1144.2016.04.022

2016-03-27

2016-04-26

云南省交通运输厅科技项目(云交科2014(A)01)

严飞(1979—)，男，云南昆明人，高级工程师，主要从事公路工程方面的工作。E-mail：yfmail621@163.com

O39；TU457

A

1672—1144(2016)04—0107—04