基于智能算法的岩石强度参数优化求解

何云松，胡　广，赵其华

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学)， 四川 成都 610059;2.成都理工大学 环境与土木工程学院， 四川 成都 610059)



基于智能算法的岩石强度参数优化求解

何云松1,2，胡广1,2，赵其华1,2

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学)， 四川 成都 610059;2.成都理工大学 环境与土木工程学院， 四川 成都 610059)

准确计算岩土体强度参数对评估岩土工程的安全性和经济性具有十分重要的意义。目前，岩石三轴实验是获取岩石强度参数(黏聚力、内摩擦角、单轴抗压强度、岩体软硬特征参数)的重要手段。大多通过试验获得轴向破坏强度σ1和对应的围压σ3后，采用手工作图或以计算机拟合包络线，以及最小二乘法求解岩石的强度参数。计算方法较多但偏重数学计算而忽视了物理意义，求解误差较大。针对上述问题，基于MATlAB语言以Mohr-Coulomb强度准则(线性准则)和Hoek-Brown强度准则(非线性准则)建立目标函数，通过粒子群算法和鱼群算法进行寻优求解。并与传统的线性回归法进行比较，通过拟合误差(Mse)分析，发现该算法求解既有优越性且能满足工程实际需求，为“模型与参数给不准”以及许多机理复杂的岩土问题的解决提供参考。

岩石强度参数；鱼群算法；粒子群算法；目标函数；优化求解

黏聚力c、内摩擦角φ、单轴抗压强度σc及岩体软硬特征参数m等是进行岩土工程设计和稳定性计算分析的基本力学参数。我国现行的国家标准《建筑地基基础设计规范》[1](GB50007-2011)并未给出明确的计算方法。目前主要采用试验直接获轴向破坏强度σ1和对应的围压σ3，依据规范拟合出σ1-σ3最佳曲线或基于强度准则拟合破坏包线，再推导出c、φ值的方法[2-5]。广泛采用的求取方法有：作图法[6]、p-q线性回归法[7]、矩法[8]和σ1-σ3线性回归法[7]等。矩法是较为常用的一种统计法，但数据样本较少时，其结果受实验误差和人为因素影响较大。同样作图法也受到人为误差的影响[8]。陈立宏等[7-8]人指出，p-q线性回归法低估凝聚力而高估摩擦系数，采用σ1-σ3线性回归能获得更合理的参数。余东明等[9]采用最小二乘正交法改进了p-q法。夏明诚[10-11]基于对原《建筑地基基础设计规范》[2](GBJ7-89)改进，提出了基于铅垂距离最小的似公切线最小二乘法求解,但王大通等[12]、陈津明[13]质疑夏文的新方法和规范一样都不满足最小二乘法的使用条件。上述争议主要存在于最小二乘法求解的适用性和强度准则误差的控制。针对工程实际问题，同样可以运用室内实验参数拟合求解[14-17]，但要对其进行相应修正。对此，一些学者尝试智能算法和优化算法，从而避免了最小二乘法求解时合理性问题，绕过了复杂的代数极值求解。仇圣华等[17]、黄润秋[18]分别采用地质统计学和优定斜率方法，对岩石三轴岩石参数进行求解，能有效的消除一定误差。陈炳初等[19]提出基于改进单纯形算法的寻优解法，根据摩尔-库仑包络线原理建立起目标函数，求解可行域内的最优解。姜照容等[20]采用BP神经网络对岩体参数进行反演，找出与反演工况下安全系数差值最小的安全系数相对应的黏聚力与内摩擦角组合,认为该组合即为最终反演的岩体抗剪强度参数。对于Hoek-Brown强度参数的求解研究较少，大多将其处理为线性关系拟合求解[21]，该方法强调数学规律而忽略了参数物理意义，有失合理性。综上所述，岩石力学参数求解中仍存在“模型与参数给不准”以及许多问题的机理不清楚等情况。为此，本文运用粒子群算法和鱼群算法较强的全局搜索能力和极强的非线性寻优特性，对以Mohr-Coulomb强度准则和Hoek-Brown强度准则建立目标函数进行寻优求解相关参数，并验证算法的应用性和优越性。为岩体质量参数求解工作提供参考。

1　三轴试验强度准则及求解

最小二乘法又称为最小平方法[10],在确定强度准则中的待定参数时,其要求全部试验数据所求得的偏差平方之和达到最小,即

δ=∑[σ1-f(σ3)]2

(1)

在实际运用中，对于式(1)中待定参数求偏导，从而得到极值点处偏导数为0的待定参数方程组，进而可求得相应的参数值。对于直线型强度准则，如Mohr-Coulomb强度准则简化为式(2)，进而通过线性回归求得强度参数值。

σ1=σc+mσ3

(2)

式中:σc为岩石单轴抗压强度；σ1和σ3分别为最大最小主应力。

严格上来说，Mohr-Coulomb强度准则切线不是相切于所有的摩尔应力圆，因此其与莫尔圆间的距离即体现了拟合精度，其示意图见图1。

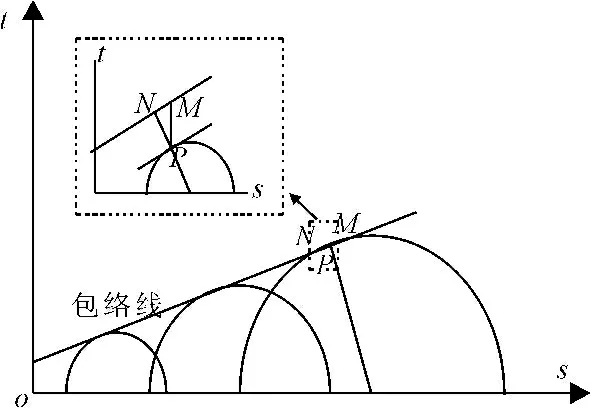
图1强度参数优化示意图(修改于文献[19])

对于参数求解精确度评价采用法向距离来评价参数优劣[9]，即定义目标函数为：

(3)

(4)

式中:c，φ为黏聚力和内摩擦角;σ1和σ3为最大最小主应力。

故综合式(3)和式(4)可得优化求解Mohr-Coulomb参数的目标函数为：

(5)

式中PN含义见图1，其中P点是基于最大剪应力原理破裂面位置而得出的，通过比较法向距离大小来评价强度参数选取的优劣。而对于非线性的Hoek-Brown准则，其表达式为

(6)

式中：m为岩石材料常数。

Hoek-Brown准则不仅属于非线性准则，而且能准确的给出岩石单轴抗拉和抗压强度，是目前最符合岩石强度特性的准则之一。Hoek-Brown准则求解亦要满足式(1)，多采用迭代求解或是转化为线性关系，再确定其未知参数。由于在非线性关系式中，极值点可能有多个，因此采用代数解法很难直接求得其参数解。故对于Hoek-Brown准则采用群智能算法求解具有极大的优越性。依式(6)Hoek-Brown准则的最佳拟合曲线，即要求与实验所得各离散点的距离之和最小，可得目标函数为：

(7)

2　群智能算法寻优解法

对于岩体强度强度参数的求解归结为一个求目标函数最优值的过程。最小二乘法是基于代数法，对目标函数求偏导，再求解方程组而得。但该方法只适用于光滑函数，对于多元函数，计算复杂，且容易限于局部最小，因此采用群智能算法(粒子群算法和鱼群算法)等数值方法，具有较大优势，且对于非线性强度准则优势将会更加显著。

2.1粒子群算法的优化求解

粒子群算法(PSO)源于对鸟类捕食行为的研究。鸟类捕食时，找到食物最简单的方法就是搜寻当前距离食物最近的鸟的周围区域。PSO将该行为用于求解最优化问题，算法中的每个粒子都代表问题的一个潜在解，每个粒子对应一个有适应度函数决定的适应度值。其本质是跟踪极值来更新粒子的位置。基于PSO算法的函数极值寻优算法流程图见图2。

图2PSO算法的函数极值寻优算法流程图

2.2鱼群算法的优化求解

人工鱼群算法是李晓磊等人于2002年提出的一类基于动物行为的群智能优化算法。该算法通过模拟鱼类的觅食、聚群、追尾、随机等行为在搜索域中进行寻优。其具有：(1) 克服局部极值、全局极值的能力；(2) 算法仅使用目标问题的函数值，对搜索空间有一定的自适应能力；(3) 对初值与参数选择不敏感，鲁棒性强，简单易实现，收敛速度快和使用灵活等特点。

本文综合运用这两种方法进行岩石参数优化求解，并与传统的线性回归法进行对比。

3　工程算例分析与验证

计算时文中岩样的选择考虑了硬质岩和软质岩，以验证优化算法的适用性；兼顾了样本数量的多少，以验证样本数据的数量对岩石参数求解的影响。文中岩石三轴实验数据来源于课题组岩石三轴实验数据(花岗岩和玄武岩)(见表1)和文献[22]中的相关实验数据(见表2)。玄武岩岩石试样取自金沙江某水电站坝区，花岗岩岩样取自金沙江上游某水电站右岸华力西期中酸性侵入花岗岩(γδ43)。岩样均按照《水利水电工程岩体试验规程》[22](SL264—2001)的相关要求和试样精度制作成直径50 mm、高100 mm的标准圆柱体，实验过程均符合相关实验要求。

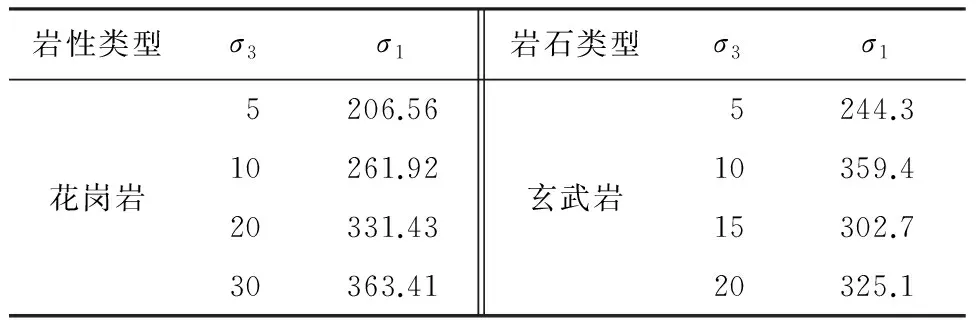
表1　相应围压下的岩石强度　单位：MPa

3.1算例分析

采用线性回归、鱼群算法和粒子群算法对岩石三轴试验数据进行计算，基于Mohr-Coulomb准则和Hoek-Brown准则求解岩石强度参数。在优化过程中分别以式(5)和式(7)建立目标函数，同时设置其相关参数(Mohr-Coulomb准则为c和φ，Hoek-Brown准则为m和σc)初始值可能计算域为(0 kPa～500 kPa，0 kPa～90 kPa)。限于篇幅原因，文中仅展示以花岗岩为算例计算Mohr-Coulomb准则相关参数的计算过程，其余结果见表3和表4。

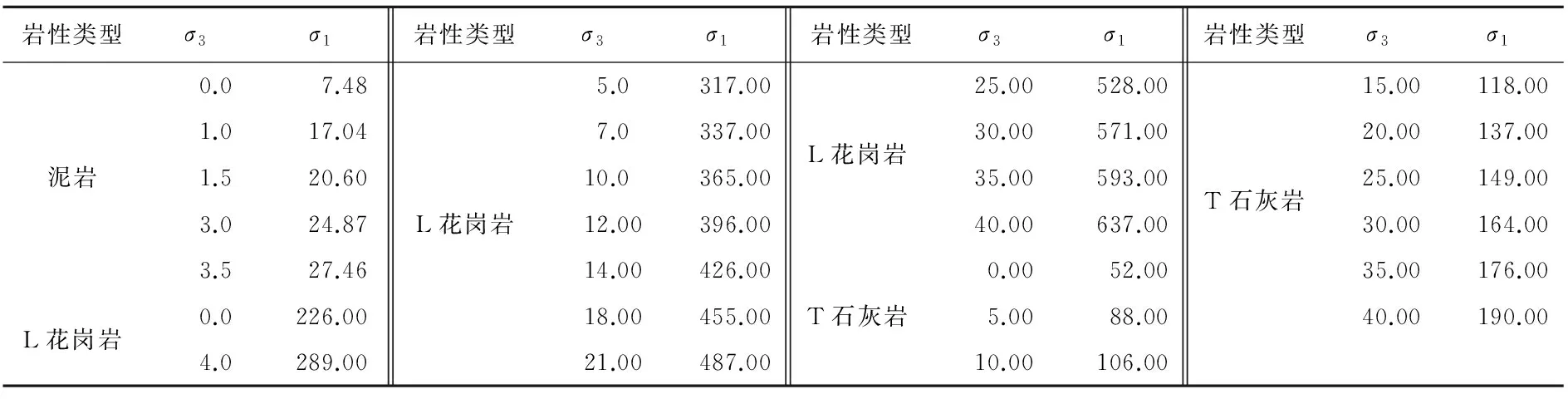
表2　相应围压下的岩石强度　单位：MPa

注：岩石实验数据来自文献[22],L花岗岩为Lac du Bonet花岗岩，T石灰岩为Tyndall石灰岩。

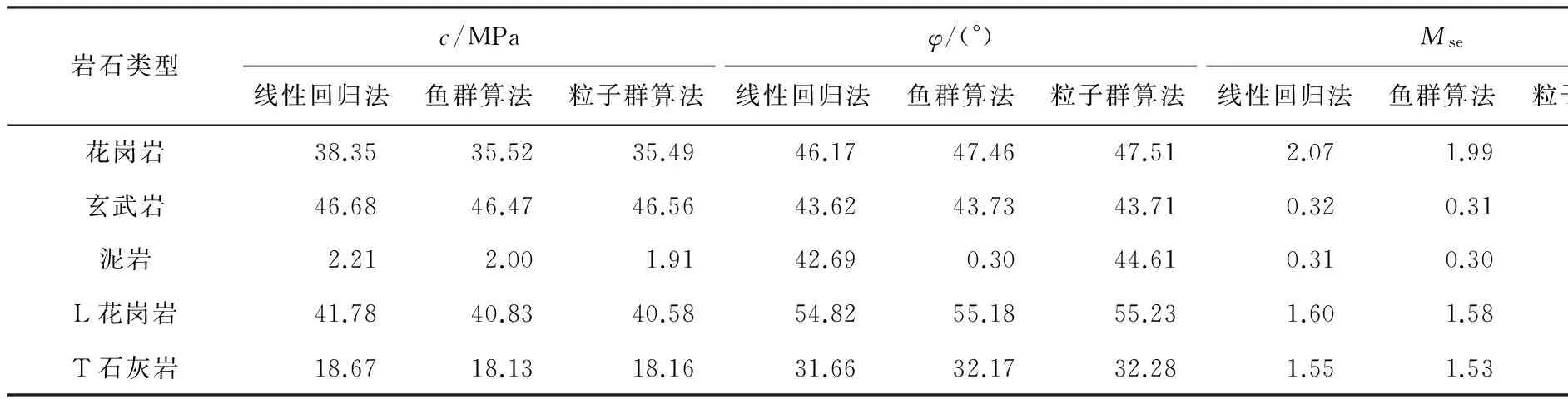
表3　不同算法的花岗岩Mohr-Coulomb准则强度参数

表4　不同算法的花岗岩Hoek-Brown准则强度参数

(1) 鱼群算法的参数设置。在仿真实验中，人工鱼数量设置300个，视野Visual=1，每次移的最大步长Step=0.1，拥挤度因子delta=0.618，迭代次数200次。由寻优坐标图可以看出，随着迭代次数的不断增加，人工鱼群不断地向最优值和局部极值移动，算法后期大部分人工鱼聚集到最优值附近，少量人工鱼聚集到个别局部极值附近。最终逼近到最优极值点。文中花岗岩求得最优解极值点坐标为：(35.52,47.46,-15.94)。其中鱼群算法迭代过程最优坐标和最优值迭代过程见图3和图4。

(2) 粒子群算法相关参数设置。依据经验，一般惯性权值ωstar=0.9，ωend=0.4时算法性能最好，随着迭代的进行，惯性权重由0.9线性递减到0.4，这样迭代初期较大的惯性权值使算法保持较强的全局搜索能力，而后期较小的惯性权值有利于局部的更精确搜索。相应的种群个数为1 000，最大迭代次数为200，算法终止阈值为1×1010。针对文中花岗岩，文中花岗岩求得最优解极值点坐标为：(35.49,47.51,15.94)。其中粒子群算法迭代过程最优坐标移动和最优值迭代过程见图5和图6。

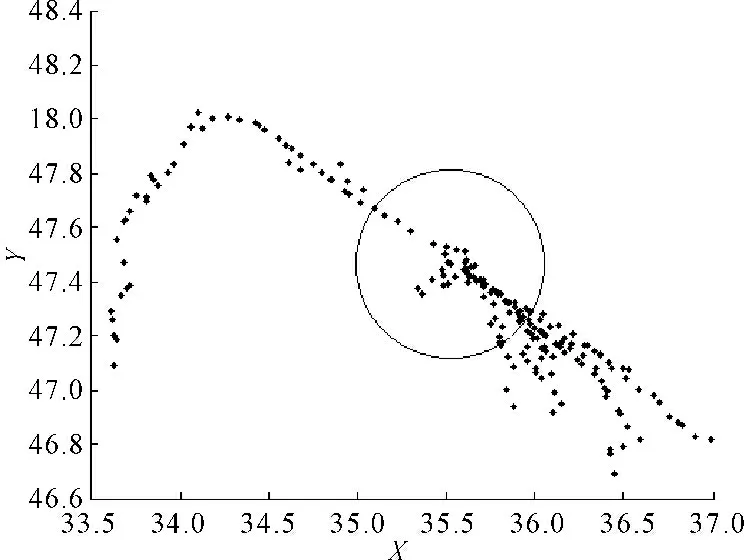
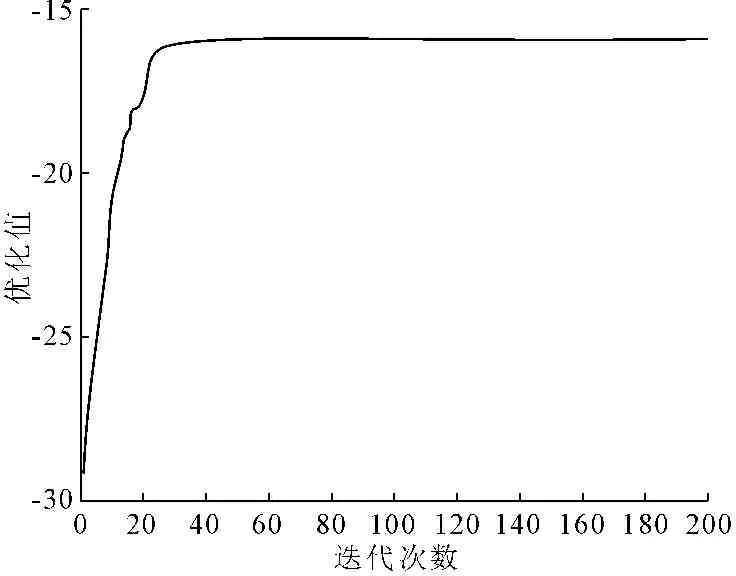
图3　鱼群算法迭代过程最优坐标移动

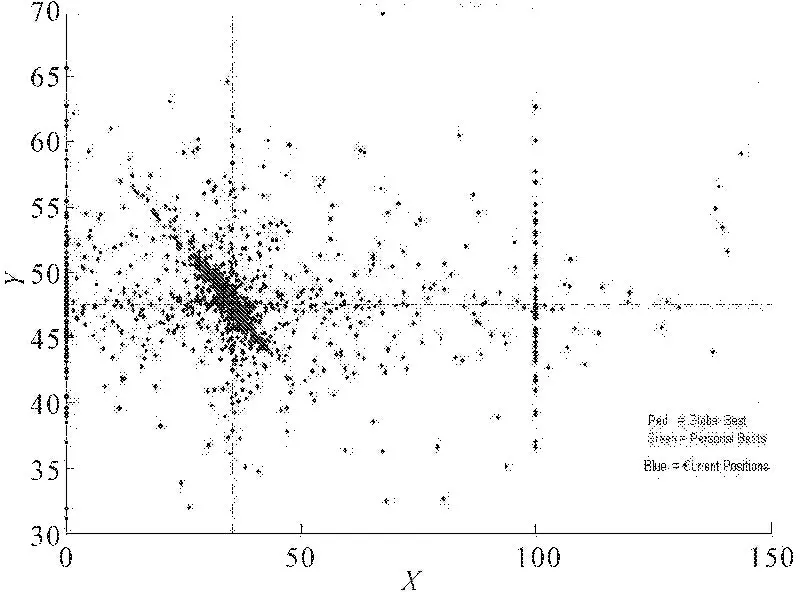
图4　粒子群算法迭代过程最优坐标移动

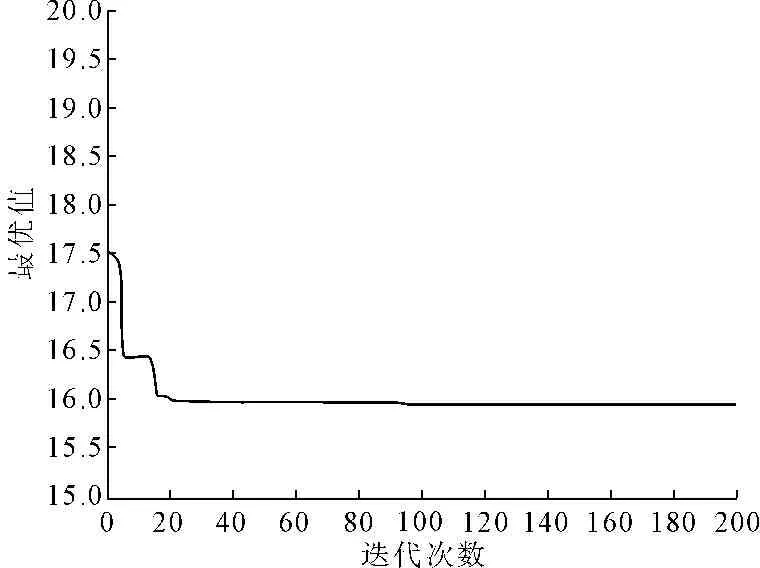
图5　鱼群算法最优值

图6粒子群算法最优值迭过程

在表3、表4中为消除不同围压样本数对法向距离D的影响，定义了Mse，其含义见式(8)。其值越小则该准则与实验数据的拟合程度越好。

(8)

式中：N为围压样本数；D为距离，见式(5)、式(7)、式(8)。

3.2算法验证

为比较不同方法的精度，将上述计算结果，表述在τ-σ坐标系中(图7)，其中莫尔圆为不同围压条件下岩样的破坏应力值，通过观察简化Mohr-Coulomb强度包线与高低围压下莫尔圆的包络程度来分析拟合模型的优越性。对于Hoek-Brown强度参数，将其计算模型表述在σ1-σ3坐标系中(图8)，观察各方法与实验数据点的拟合程度来评价Hoek-Brown模型的精度。另外，通过式(8)定义的Mse来评价群智能算法在模型参数优化求解中的适用性和优越性(图9)。文中选取了花岗岩和T石灰岩进行了分析，限于篇幅，其余不做赘述。

由图7可以看出，基于粒子群和鱼群算法计算得到的黏聚力c普遍比线性回归法偏小，而内摩擦角φ偏大。改进Mohr-Coulomb包络线更加贴合低围压应力圆，则偏离高围压应力圆，与Mohr-Coulomb准则更适用于低围压条件是一致的。在图8中，改进的Hoek-Brown包络线更加贴合各围压应力圆，与拉应力圆更接近。这与Hoek-Brown准则属于非线性准则且能准确的给出岩石的单轴抗拉和抗压强度的特性相符，体现了群智能算法在非线性优化求解过程中极大优势。图9中，基于优化算法的求解的模型拟合Mse均小于传统算法，特别对于Hoek-Brown(非线性)强度准则，其优势更明显。另外数据的多少，对模型参数的求解影响不大。

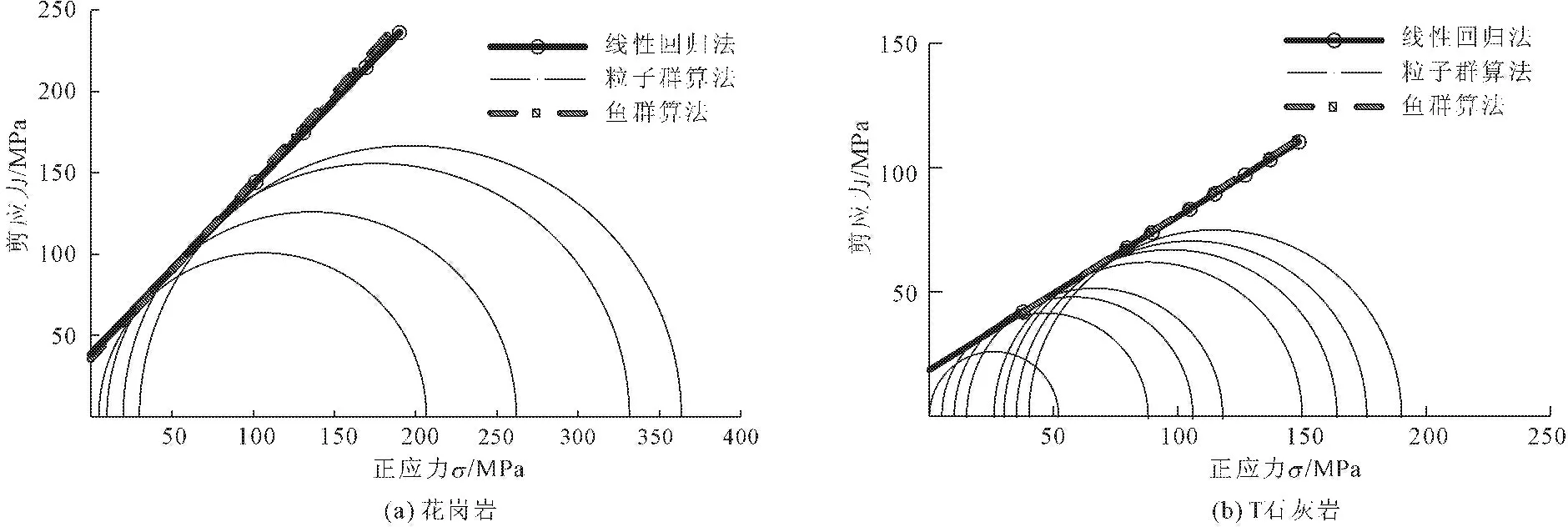
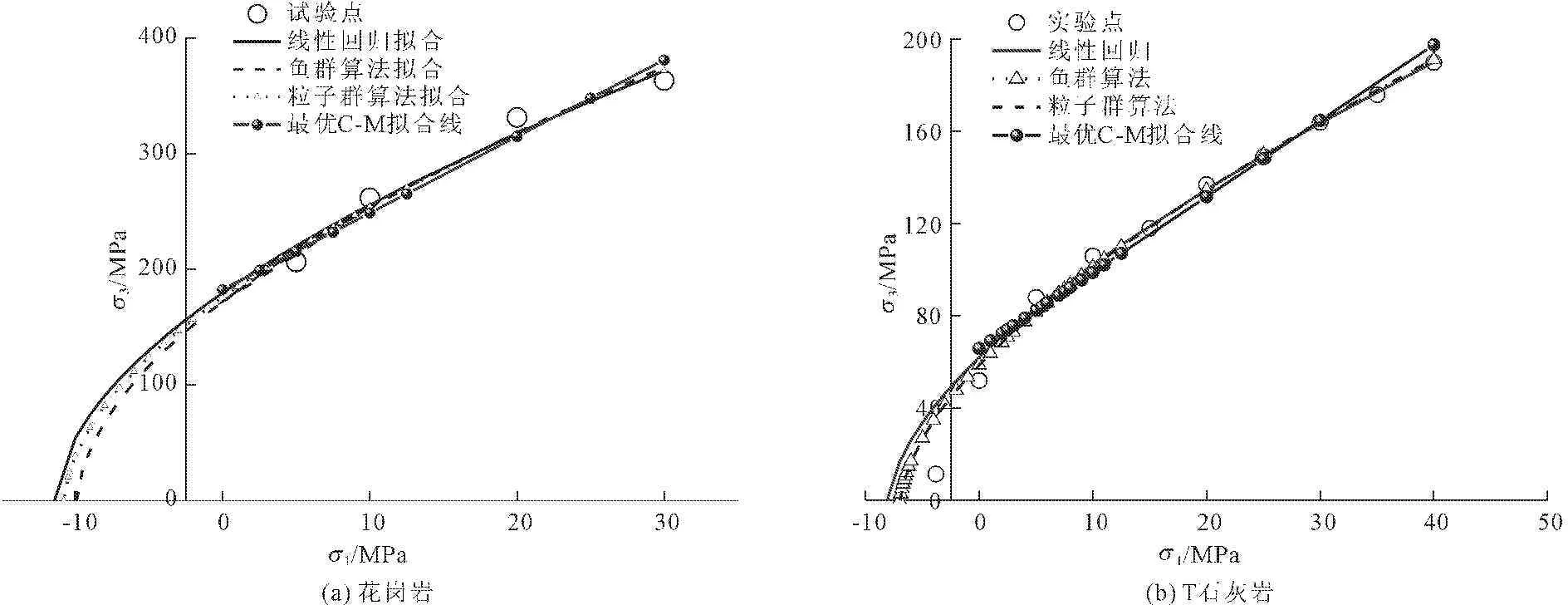
图7　不同计算方法Mohr-Coulomb准则强度参数对比

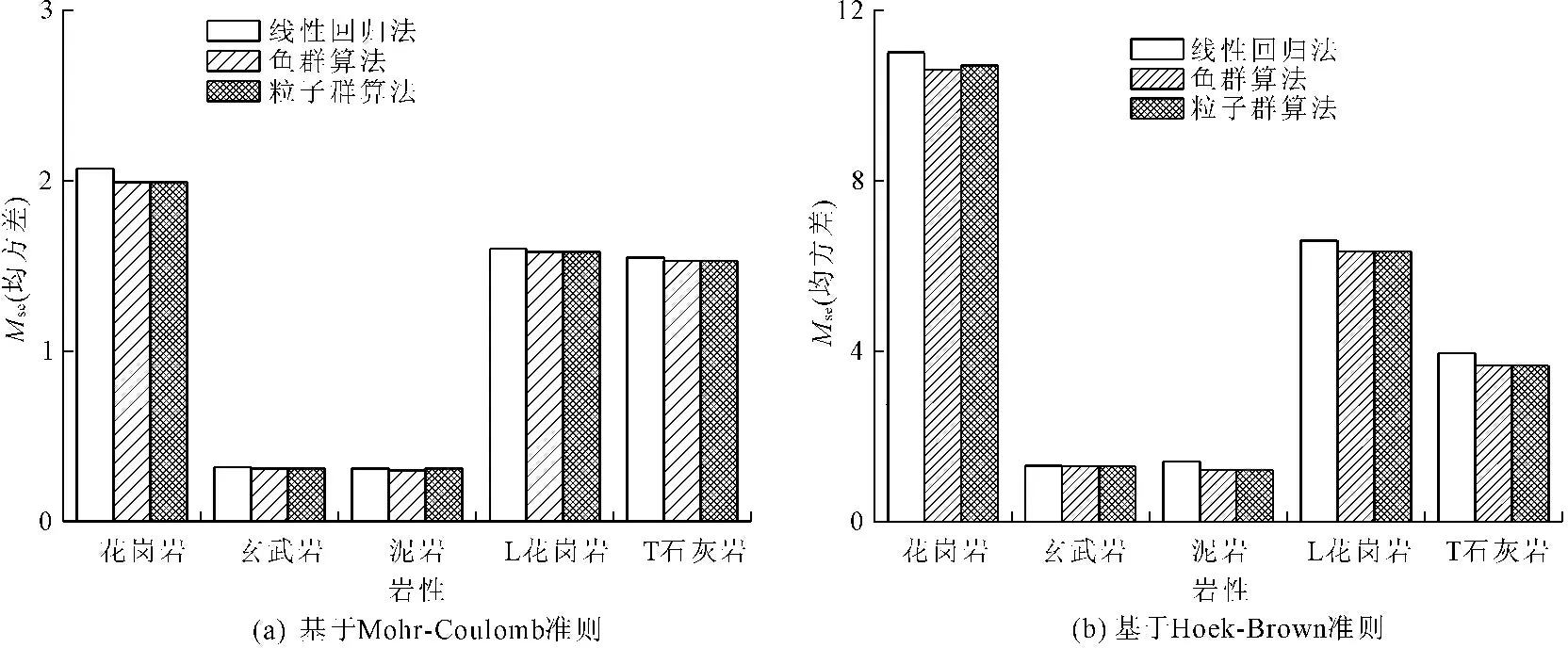
图8　不同计算方法Hoek-Brown准则强度参数对比

图9不同方法的参数对比

4　结　论

本文基于Mohr-Coulomb(线性)强度准则和Hoek-Brown(非线性)强度准则，采用了粒子群算法、鱼群算法进行计算，并与传统线性回归法进行比较。得出以下结论：

(1) 群智能算法极值寻优区别于传统的最小二乘法代数求导法，具有较强的全局搜索能力和极强的非线性寻优特性，所得参数与实验数据拟合较好，且更符合工程实际。

(2) 智能算法计算得到的黏聚力c普遍比线性回归法偏小，而内摩擦角φ偏大。改进Mohr-Coulomb包络线更加贴合低围压应力圆，偏离高围压应力圆，与Mohr-Coulomb准则更适用于低围压条件一致。

(3) 改进Hoek-Brown包络线与各围压应力圆拟合较好，且与拉应力圆更接近，这与Hoek-Brown准则属于非线性准则，且能准确的给出岩石的单轴抗拉和抗压强度的特性相符。

(4) 岩石工程中常遇到“模型与参数给不准”以及机理仍不清楚等问题，智能群算法较强的全局搜索能力和极强的非线性寻优特性能准确求解最优解，能有效解决代数 寻优工作量大，计算复杂，极值难以确定的缺点。因而具有极大的推广前景。

[1]中华人民共和国住房和城乡建设部.建筑地基基础设计规范：GB50007-2011[S].北京:中国建筑工业出版社,2011：127-128.

[2]中华人民共和国住房和城乡建设部.建筑地基基础设计规范：GBJ7-89[S].北京:中国建筑工业出版社,1989：79-80.

[3]中华人民共和国交通部.公路土工试验规程：JTGE40-2007[S].北京:人民交通出版社,2007：293-399.

[4]中华人民共和国国家发展和改革委员会.水电水利工程岩石试验规程：DL/T5368-2007[S].北京:中国电力出版社,2007：126-127.

[5]张永兴，等.岩石力学[M].2版.北京:中国建筑工业出版社,2008：315-17.

[6]刘善均,王韦,许唯临.莫尔圆求解c、φ值的最佳拟合[J].四川大学学报(工程科学版),2002,34(6):40-42.

[7]陈立宏,陈祖煜,李广信.三轴试验抗剪强度指标线性回归方法的讨论[J].岩土力学,2005,26(11):1785-1789.

[8]陈立宏,陈祖煜,李广信.线性回归抗剪强度指标方法的改进[J].岩土力学,2007,28(7):1421-1426.

[9]余东明,姚海林,吴少锋.三轴试验抗剪强度参数值回归分析法的区别与修正[J].岩土力学,2012,33(10):3037-3042.

[10]夏明诫,用三轴试验结果求c,φ值的一种新的解析算法[J].土工基础，1998,12(3):48-51.

[11]夏明诚.再谈抗剪强度c,φ标准值的统计方法问题[J].岩土力学,1997,18(3):88-92．

[12]王大通,熊启东．对“关于抗剪强度c,φ值统计方法的思考”一文的讨论[J]．岩土力学,1998,19(1):88-89．

[13]陈津民．质疑“用三轴试验结果求c,φ值的一种新的解析算法”[J].岩土工程界,2007,10(8):22-24.

[14]牛庆明,朱华.地下水封储油洞库岩体力学参数试验研究[J].水利与建筑工程学报,2014，12(6):176-180.

[15]张丽萍,刘超.公路滑坡滑带土抗剪强度参数选取方法研究[J].水利与建筑工程学报,2012,10(1):57-59.

[16]田延哲,徐拴海.露天矿边坡稳定性评价岩体力学参数修正[J].水利与建筑工程学报,2014，12(6):112-117.

[17]仇圣华,杨林德,陈岗.地质统计学理论在岩体参数求解中的应用[J].岩石力学与工程学报,2005,24(9):1545-1548.

[18]黄润秋,许模,柴贺军，等.金沙江溪洛渡水电工程岩体结构模型及其工程应用研究[R].成都:成都理工学院,1997:320-330.

[19]陈炳初,赵明华.抗剪强度c,φ求取的改进单纯形寻优解法[J].湖南大学学报(自然科学版),2009,36(2):18-21.

[21]姜照容,王乐华.岩体抗剪强度参数神经网络反分析方法改进[J].长江科学院院报,2014,31(6):42-47.

[22]付义胜.常规三轴强度准则对试验数据的拟合和评价[D].焦作：河南理工大学,2012.

Rock Strength Parameters Optimization Based on Intelligent Algorithm

HE Yunsong1,2, HU Guang1,2, ZHAO Qihua1,2

(1.StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection(ChengduUniversityofTechnology),Chengdu,Sichuan610059,China; 2.ChengduUniversityofTechnologyCollegeofEnvironmentandCivilEngineering,Chengdu,Sichuan610059,China)

Rock triaxial experiment is an important way to obtain rock strength parameters, such as cohesive force, angle of internal friction, uniaxial compressive strength, hard or soft characteristic parameters of rock. After the axial failure strength and the corresponding confining pressure were obtained by experiments, the strength parameters of rock could be solved by hand or computer fitting envelope, and the least square method. There are some calculative methods, which emphasizes on mathematical calculation and neglects the physical meaning as well as large error. So based on Mohr-Coulomb strength criterion (linear criterion) and Hoek-Brown strength criterion (nonlinear criterion) by using Matlab, the problem was then solved by using intelligent algorithms particle swarm optimization algorithm and the fish swarm algorithm. Finally the results were compared with the traditional linear regression method with fitting error(Mse) analysis, it is found that the algorithm is superior and can meet the engineering requirements. For the model and the parameters are vague, as well as a number of issues to provide reference for the solution of complex geotechnical problems.

rock strength parameter; fish swarm algorithm; particle swarm optimization algorithm; objective function; optimization solution

10.3969/j.issn.1672-1144.2016.04.016

2016-03-28

2016-04-21

国家自然科学基金项目(41272333)

何云松(1991—)，男，云南红河人，硕士研究生，研究方向为岩土工程。 E-mail：1587749967@qq.com

赵其华(1965—)，男，江苏泰兴人，教授，博导，主要从事岩土工程方面的研究工作。 E-mail：zhqh@163.com

TU192

A

1672—1144(2016)04—0078—06