改进粒子群结合K-均值聚类的图像分割算法

邬春学，刘训洋

(上海理工大学 光电信息与计算机工程学院，上海 200093)



改进粒子群结合K-均值聚类的图像分割算法

邬春学，刘训洋

(上海理工大学 光电信息与计算机工程学院，上海 200093)

K-均值聚类的分类结果过分依赖于初始中心的选择且容易陷入局部最优。文中针对K-均值的缺陷，提出了一种基于随机权重粒子群和K-均值聚类的图像分割算法RWPSO-KM。在算法开始，利用随机权重粒子群算法的全局搜索能力避免算法陷入局部最优。然后根据公式计算种群多样性执行K-均值算法，利用K-均值算法的局部搜索能力实现算法的快速收敛。实验结果表明, RWPSO-KM与K-均值聚类和PSOK相比具有更好的分割效果和更高的分割效率。

K-均值聚类；随机权重粒子群；图像分割

图像分割指的是根据灰度、颜色、纹理和形状等特征把图像划分成若干互不交迭的区域，并使这些特征在同一区域内呈现出相似性，而在不同区域间呈现出明显的差异性[1]。图像分割是图像处理过程中的基础环节，是由图像处理到图像分析的关键步骤[2]。聚类[3-4]分析是数据挖掘的重要手段，聚类算法应用于图像分割时能够获得较好的分割效果而得到了广泛关注和应用。

K-means[5]算法是该类方法中比较常用的一种算法，这种方法首先选定某种距离度量作为元素间的相似性度量，然后确定某个评价聚类划分结果质量的准则函数，在给出聚类中心点后，用迭代的方法找出使准则函数取极大值或极小值的最好聚类结果。但是，K-均值算法的聚类结果依赖于初始值的选取，并且基于梯度下降进行搜索常常使算法陷入局部最优。Kennedy 和Eberhart[6]于1995 年提出的粒子群优化(Particle Swarm Optimization,PSO)算法，由于其收敛速度较快[7]，需要设置和调整的参数较少，算法实现比较简单，一直以来受到学术界的广泛重视。PSO 算法具有较强的全局寻优能力，通过适当调整权重系数，可以提高全局搜索能力，满足不同的应用场合。因为PSO算法具有较强的全局寻优能力而K-均值算法局部寻优效果好，所以陶新民等[8-9]用PSO改进K-均值(PSOK)来进行图像分割，取得了一定的效果。但如何将PSO算法和K-均值聚类更好的结合发挥各自的优势[10-11]，仍是图像分割研究的热点问题。

本文提出一种随机权重粒子群算法和K-均值相结合的图像分割方法RWPSO-KM。针对PSO算法缺点进行改进(RWPSO)并提出群多样性测量方法来实现从RWPSO到K-means的切换。

1　K-均值聚类算法

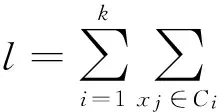
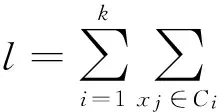
(1)

当函数取最小值时，计算聚类中心

(2)

其中,ni是第i组的数据点个数。然后不断更新聚类中心使同一个类中的数据点相似性不断增大，不同的类之间的数据点相似性越来越小，从而达到聚类目的。

2　粒子群优化算法

粒子子群优化算法最初是由Kennedy和Eberhart于1995年受人工生命研究结果启发, 在模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的进化计算技术。与其他进化寻优算法相类似，PSO通过个体间的协作与竞争, 实现多维空间中最优解的搜索。

PSO算法不像遗传算法那样对个体进行选择、交叉和变异操作, 而是将群体中的每个个体视为多维搜索空间中一个没有质量和体积的粒子，这些粒子在搜索空间中以一定的速度飞行, 并根据粒子本身的飞行经验以及同伴的飞行经验对自身的飞行速度进行动态调整, 即每个粒子通过统计迭代过程中自身的最优值和群体的最优值来不断修正自己的前进方向和速度大小, 从而形成群体寻优的正反馈机制。PSO算法就是这样依据每个粒子对环境的适应度将个体逐步移到较优的区域, 并最终搜索、寻找到问题的最优解。

设在d维搜索空间内粒子i的位置为Xi=(xi1,xi2,…,xid)，速度为Vi=(vi1,vi2,…,vid)。在迭代过程中，粒子发现本地最优解为 ，整个群体目前找到的全局最优解 ，则迭代中粒子i的速度更新公式为

vij(t+1)=wvij(t)+c1r1(pij-xij(t))+c2r2(pgj-xij(t))

(3)

其中，w是惯性重量；c1、c2是加速度常数，取值在0～4之间，r1和r2为0～1之间均匀分布的随机数。粒子 的位置更新公式为

xij(t+1)=xij(t)+vij(t+1),j=1,2,…,d

(4)

3　RWPSO算法

虽然PSO广受欢迎，因为它简单的概念、较少的参数、且易于实现，它也有过早收敛的问题，特别是在大型复杂的问题。观察式(1)可以看出，粒子速度收敛快粒子飞行速度V(t)快速下降趋于0，即|V(t+1)|>|V(t)|的概率太小甚至为0，粒子活性缺失，使得粒子很难跳出局部极值区域，这就是PSO算法容易陷入过早收敛的原因。文献[2]提出的ARPSO算法根据一定的评判标准来判定粒子活性的大小，当粒子活性很小时就使粒子发散。但粒子活性评判标准的计算量远大于粒子速度和位置变化公式的计算量，因此该方法并不实用。

要使粒子速度发散概率较大必须降低粒子收敛速度，保持粒子活性和算法的多样性。本文提出一种惯性权重因子在一定范围内随机取值并且去掉随机参数r1和r2的改进PSO算法RWPSO。其速度更新公式为

vij(t+1)=w(t)vij(t)+c1(pij-xij(t))+c2(pgj-xij(t))

(5)

其中，w(t)是在一定范围内的随机值，使其满足c1+c2>2(w+1)，这样粒子的速度有可能收敛也有可能发散，保证了种群的多样性。

种群多样性测量公式如下

(6)

4　RWPSO-KM 算法

4.1算法思想

RWPSO-KM 算法在图像分割时主要分为两个阶段。算法前期使用RWPSO算法搜索整个解空间，寻找全局最优解。当RWPSO算法搜索到全局最优解时，算法切换到K-means算法，并将搜索到的全局最优解作为K-means聚类的初始聚类中心。在算法的后期阶段，按照K-means算法进行局部的寻优。这样RWPSO-KM算法既利用了 PSO算法的全局搜索能力，又保持了K-means算法的局部寻优能力，同时克服了K-means算法容易陷入局部最优的缺点。

4.2粒子适应度计算

首先在数据点集合X中随机选取m个数据点作为初始聚类中心，作为优化问题的解空间(m个粒子)。当聚类中心确定后将集合X中n个数据点分配到这m个类，设xi为集合X的第i个数据点，cj为第j个聚类中心，当‖xi-cj‖取最小值时将xi分配到第j类。第i个粒子的适应度为

(7)

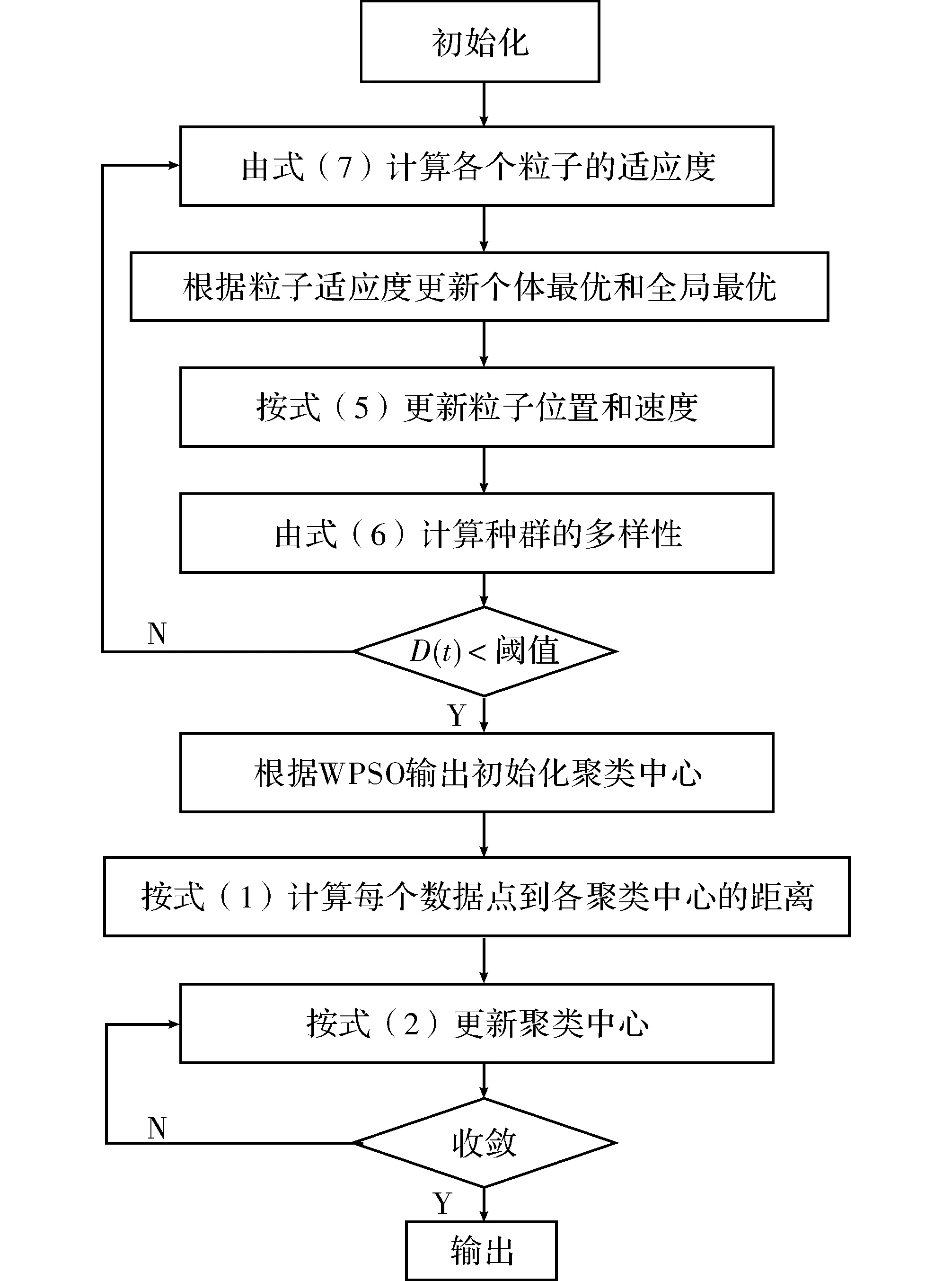
图1　RWPSO-KM算法流程图

5　仿真实验

为验证算法的优势，在Matlab 环境下对3幅图像分别采用K-means，PSOK和RWPSO-KM算法进行了图像分割实验。实验图像为Lenna(图像大小768 kB，512×512像素)；Baboon(图像大小703 kB，500×480像素)；Barbara(图像大小1.18 MB，720×576像素)。

图2第1行分别为Lenna原图、K-均值算法实验结果和PSOK算法实验结果、RWPSO-KM算法结果。可以看出在人物眼睛和眉毛、嘴唇和下巴以及冒顶的头发等处，PSOK算法和RWPSO-KM算法比K-均值算法有更加的分割效果，RWPSO-KM算法比PSOK算法和K-均值算法更加细致。图2中第2行分别为Baboon原图、K-均值算法实验结果和PSOK算法实验结果、RWPSO-KM算法结果。可以看出在狒狒的眼睛和鼻子等处，PSOK算法和RWPSO-KM算法比K-均值算法有更好的分割效果，RWPSO-KM算法比PSOK算法和K-均值算法更加细致。图2第3行分别为Barbara原图、K-均值算法实验结果、PSOK算法实验结果和RWPSO-KM算法结果。可以看出3种算法分割效果差异不大，原因在于原图中的物体和人物分别在颜色和形状上存在明显的差别，算法能较好地分割。

图2　3种算法实验结果

在对3幅图像进行图像分割实验的同时，对K-均值、PSOK 和本文RWPSO-KM 这3种算法的运行时间进行比较，比较结果如表1 所示。

表1　算法的运行时间比较　　　　　/ms

如表1所示，虽然测试的图像不同但对于每一幅图像来说本文提出的RWPSO-KM 算法比PSO算法和K-means算法的运行时间都少，该算法效率占优。

6　结束语

本文针对K-均值聚类算法对初始聚类中心选择敏感，后期收敛速度慢一般以局部最优结束的缺陷，用粒子群优化算法RWPSO加以改进。RWPSO-KM算法既保留了K-均值收敛速度快的优势，又能避免K-均值易陷入局部最优的缺点。实验结果表明，RWPSO-KM算法比K-均值和PSOK算法在图像分割效果和效率方面都有较大的提高。

[1]王爱民,沈兰荪. 图像分割研究综述[J]. 测控技术, 2004, 19(5):1-6.

[2]许新征,丁世飞,史忠植,等. 图像分割的新理论和新方法[J]. 电子学报, 2010, 38(2A): 76-82.

[3]Fu K S, Mui J. A survey on image segmentation[J].Pattern Recognition,1981,13(1):3-16.

[4]Halkidi M, Batistakis Y,Vazirgiannis M. On clustering validation techniques[J]. Journal of Intelligent Information Systems, 2001, 17(2-3):107-145.

[5]陈金山,韦岗. 遗传+模糊C-均值混合聚类算法[J].电子与信息学报, 2002, 24(2):210-215.

[6]Kennedy J, Eberhart R. Particle swarm optimization [C].Perth, Australia: Proceedings of the 1995 IEEE International Conference on Neural Networks, 1995.

[7]曾建潮,崔志华. 一种保证全局收敛的PSO算法[J]. 计算机研究与发展, 2004, 41(8): 1333-1338.

[8]陶新民,徐晶,杨立标,等. 一种改进的粒子群和 K 均值混合聚类算法[J]. 电子与信息学报, 2010,32(1): 92-97.

[9]时颢,赖惠成,覃锡忠. 粒子群与K均值混合聚类的棉花图像分割算法[J]. 计算机工程与应用, 2013,49(21): 226-229.

[10]赫然,王永吉,王青,等. 一种改进的自适应逃逸微粒群算法及实验分析[J]. 软件学报, 2006, 16(12):2036-2044.

[11]刘靖明,韩丽川,侯立文. 基于粒子群的K均值聚类算法[J]. 系统工程理论与实践, 2005, 25(6):54-58.

A Modified PSO Combined K-Means Clustering Algorithm for Image Segmentation

WU Chunxue, LIU Xunyang

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

The heavy dependence of the K-means clustering classification on selecting of the initial centers makes it easy to fall into local optimum. A RWPSO-KM based on random weight particle swarm algorithm and K-means algorithm is proposed. The global search capability of random weight particle swarm optimization algorithm is used first to avoid falling into local optimum, after which the population diversity is calculated according to the formula to execute K-means algorithm, and the local search of K-means algorithm is employed to achieve fast convergence. Experimental results show that RWPSO-KM is superior to K-means clustering and PSOK in segmentation effect and efficiency.

K-means clustering; random weight particle swarm; segmentation

10.16180/j.cnki.issn1007-7820.2016.08.027

2015-11-29

国家自然科学基金资助项目(61202376)

刘训洋(1991-)，男，硕士研究生。研究方向：图像分割。

TP391.41

A

1007-7820(2016)08-093-04