基于回溯的最大频繁项集挖掘算法

张心静，于嘉威，王红梅

(长春工业大学 计算机科学与工程学院，吉林 长春 130012)



基于回溯的最大频繁项集挖掘算法

张心静，于嘉威，王红梅

(长春工业大学 计算机科学与工程学院，吉林 长春 130012)

针对Apriori类算法多次扫描数据库和FP-tree类算法需要构建大量条件模式树的问题，文中提出了挖掘最大频繁项集的GBMFI算法。采用垂直格式存储事务数据库，以枚举树为基础，利用子集非频繁性质和父子节点支持度信息在搜索过程中对枚举树进行剪枝，最终得到最大频繁项集。通过实验对比，结果证明了算法的有效性，尤其适用于稀疏数据集。

数据挖掘；最大频繁项集；关联规则；回溯法；剪枝

随着大数据时代的发展，数据挖掘技术在这个领域发挥的作用变得不可小觑[1]。发现关联规则是数据挖掘工作的重点。而挖掘频繁项集又是寻找关联规则的重要步骤之一。但在通常情况下得到的频繁项集数量庞大，且彼此之间存在项重复的现象，这就导致了信息冗余的问题。由于最大频繁项集隐含了所有频繁项集的信息，大幅缩减了频繁项集的数量，因此挖掘最大频繁项集的任务应运而生。挖掘最大频繁项集的算法通常基于Apriori[2]和FP-tree[3]思想。一方面，基于Apriori改进的算法自底向上逐渐产生所有频繁项集，但在这一过程中也会因连接操作生成大量的候选项集，同时为了削减候选项集，导致算法多次扫描整个事务数据库，耗费了时间与资源。尤其是针对大数据进行处理时，产生的项集规模过大使得计算机难以对其进行存储与计算，高效得到价值密度高的数据更加困难。另一方面，研究者们基于FP-tree提出一些挖掘最大频繁项集的算法，如MaxSP[4]，DMFIF[5]，MMFI[6]，IMMFIA[7]，FP-MFIA[8]等算法。然而多数基于FP-tree的算法，利用递归调用不断产生条件模式树的方法得到最大频繁项集，因此需要构建大量的条件模式树，消耗了巨大的时空资源。此外，研究发现，学者大多是对最小支持度与算法运行时间的关系进行实验，对结果的数量及其分布情况缺少较为详尽的记录。

基于上述理论研究，本文提出了GBMFI算法。通过在标准数据集中进行实验，分别记录了算法的运行时间，最大频繁项集的个数以及不同长度下最大频繁项集的分布情况，尤其是对最小支持度和最大频繁项集个数的关系进行了研究。另外，GBMFI与DepthProject进行了实验对比。DepthProject作为挖掘最大频繁项集的经典算法，采用深度优先搜索策略，虽然使用了压缩效率较高的水平二进制表示事务数据库，但本文采用的垂直位图表示形式可更快速的计算支持度。结果证明了GBMFI的有效性，尤其适用于稀疏数据集。

1　理论基础

定义1 设I={I1,I2,I2,…,Im}是所有项的集合，其中Ii(1≤i≤m)称为项。若集合X⊆I，则称X为项集。设TDB={T1,T2,T3,…,Tn}是所有事务的集合，称为事务数据库。其中，Ti(1≤i≤n)称为事务，且每个事务Ti是项的集合，满足Ti⊆I。对应每一个事务都有唯一标识符事务号，记作TID。通常项在事务中有序;

定义2 项集长度k是指项集中包含的项的个数。长度为k的项集称为k项集;

定义3 已知项集X⊆I，将X在TDB中出现的次数作为项集X的支持度，记作Sup(X)，即包含X的事务数;

定义4 设最小支持度阈值为min_sup。Sup(X)≥min_sup, 则称X是频繁项集。若项集X在数据库中是频繁的，对任意满足X⊂y的项集Y而言，Y是X的超集且是不频繁的，则X为最大频繁项集。假设数据库中的事务数为M，则min_sup也可用百分比表示，则最小支持度阈值可用最小支持度百分比乘以事务数M求得;

定义5[9]将数据库中出现的所有项按词典序排列，逻辑上组织成枚举树的形式。第0层是根，为空。第k层包含了所有的k项集。树中每个节点由两部分组成，分别是节点的头部Head和节点的尾部Tail。Head其实就是节点本身所代表的项集。Tail为节点可扩展的项的集合。注意，Tail包含了所有按照字典序大于Head的项元素。如图1所示，假设所有项的集合为{a,b,c}，图中“()”内表示Head，“{}”内表示Tail。

图1　枚举树

性质1 (子集非频繁剪枝[10])若X是非频繁项集，则任何X的超集Y均是非频繁项集。在深度搜索过程中，利用此性质可对枚举树进行剪枝;

性质2 (父等价剪枝[11])设当前节点为X，i∈Tail(C)。若Sup(C∪{i})=Sup(C)且Sup(C∪{i})≥min_sup，可直接从节点指向C∪{i}遍历。

证明：反证法。假设存在Z=C∪{j}(j∈TailC),j≠i，Z⊆M但iM且m频繁。由于Sup(C∪{i})=Sup(C)，且Sup(C∪{i})≥min_sup，存在C的频繁项集中一定存在i。这与iM矛盾。因此包含C而不包含i的项集中不会出现最大频繁项集。证毕。

2　GBMFI算法

准备工作：扫描事务数据库TDB，将水平表示[13]的数据库(如表1所示)转换为垂直表示[12]形式(如表2所示)。若项x在事务y中存在，则在相应位置标1，否则标0。通过计数得到各1项集的支持度，再利用min_sup约束得到频繁1项集F1，并将F1按支持度升序排列。

表1　水平表示的事务数据库

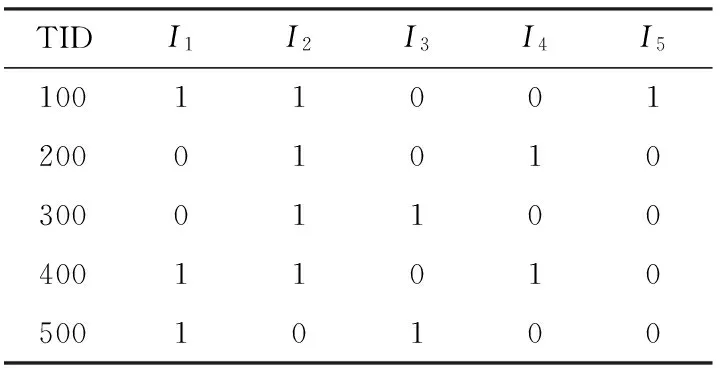
表2　垂直表示的事务数据库

初始条件：节点R为根节点。Head(R)=Ø。Tail(R)=F1。结果集MFI=Ø。令当前节点C=R∪{i}(i为Tail(R)中第一个项)，即选择节点R的第一个孩子节点作为起始节点。

算法过程：GBMFI(C,MFI)

(1)计算当前节点C的头尾并集Un=Head(C)∪Tail(C)；

(2)检测Un是否已被MFI包含。若是，则终止扩展，并将当前节点指向C的第一个右兄弟RB，然后执行GBMFI(RB,MFI)。否则，执行(3)；

(3)依次计算C∪{i}(i∈Tail(C))的支持度。若Sup(C∪{i})≥min_sup且Sup(C∪{i})=Sup(C)，则执行步骤(4)。若Sup(C∪{i})

(4)将当前节点指向Cn=C∪{i}(i为ReducedTail(C)中第一个项)。更新当前节点Cn的Tail，继续执行GBMFI(Cn,MFI);

(5)若该节点是叶子节点(Tail(C)=Ø)，且通过检测发现MFI中不存在其超集，则将其加入到结果集MFI中。否则回溯到根节点R，在Tail(R)中选择未被扩展的第一个孩子作为当前节点FC，执行GBMFI(FC,MFI)；

(6)直到Tail(R)均被处理完，算法结束。

3　实验与结论

实验环境为Windows7 64位s操作系统。Intel(R)Core(TM)i5-3230M CPU@2.60 GHz。内存6.00 GB，使用C++语言进行编程。为测试该算法的有效性，本文选取了数据挖掘实验中2个典型的标准数据集，如表3所示。分别记录了不同数据集下的算法运行时间，并与DepthProject的运行时间做了对比。同时还记录了最大频繁项集结果数以及不同长度的最大频繁项集的分布情况。

表3　测试数据集特征

3.1T10I4D100K实验结果及分析

T10I4D100K是由1 000个项组成，较为稀疏，频繁项集长度较短。表4记录了不同min_sup下最大频繁项集的结果数以及GBMFI和DepthProject的执行时间。min_sup用百分比的形式，单位是%，结果的单位是个，时间单位s，T(G)代表GBMFI的执行时间，T(D)代表DepthProject的执行时间。图2给出了最大频繁项集的详细分布图，横坐标为项集长度，纵坐标为个数。根据表4可知，随着min_sup的增大，挖掘出的最大频繁项集数量也越来越少，则运行时间越来越小。同时可看出，GBMFI的运行速度高于DepthProject。当最小支持度较大，例如min_sup为0.05%时，两者运行时间相差很小。GBMFI的运行时间为27.9 s，而DepthProject的运行时间为34.1 s。随着最小支持度减小，两者的运行时间相差逐渐变大。例如当min_sup为0.01%时，GBMFI的运行时间为44.2 s，而Depth Project的运行时间为56.5 s。图2显示出min_sup为0.02%时，最大频繁项集的分布详情。由图可知，最大频繁项集的结果主要集中长度为2和长度为3的地方，最长的最大频繁项集长度为10。在长度为10的情况下，结果数为个位数，得到的最大频繁项集较少。因此，在这一数据集中得到的最大频繁项集较短。

表4　T10I4D100K下的min_sup与结果数、算法时间的关系

图2　min_sup为0.02%时，T10I4D100K下的结果分布图

3.2Chess的实验结果及分析

Chess是从国际象棋比赛中获取的数据，属于稠密型数据集。从表5可知，随着min_sup增大，最大频繁项集的结果数也越来越少，而运行时间越来越小，且GBMFI的运行速度优与DepthProject，例如当min_sup为14%时，GBMFI的运行时间为45.2 s，而DepthProject的运行时间为58.7 s。但对比T10I4D100K可知，相对与Chess本身的大小而言，从Chess中得到结果的数量非常多。这是由于Chess中事务之间较为相似，数据的密集性导致了频繁项集的数量巨大以及复杂的计算性。这也使得Chess被作为具有权威性的频繁项集挖掘算法的测试数据集。图3显示出最大频繁项集的长度多集中为10、11、12，且结果长度可达25。

表5　Chess下的min_sup与结果数、算法时间的关系

图3　min_sup为5%时，Chess下的结果分布图

综合以上对数据集的实验结果可知，随着min_sup增加，GBMFI运行时间越来越小，得到的最大频繁项集也越来越少。对比DepthProject可知，GBMFI时间性能较好。而对稀疏数据集而言，结果多集中在长度较短的地方，得到的最大频繁项集数量相对较少，因此运行时间更少。相反，从稠密数据集中得到的结果相对较长。若数据集中的事务较短，那么得到的结果也较短。否则，得到的最大频繁项集也较长。另外，由于数据集之间存在差异性，因此针对不同的数据集文中要选取适合该数据集的最小支持度做测试，而不能使用相同的最小支持度阈值。

4　结束语

挖掘最大频繁项集可作为压缩频繁项集的一种方法，也可是大数据环境下节省存储空间的一种手段。针对数据挖掘中最大频繁项集的挖掘问题，本文提出了一种基于回溯法的最大频繁项集挖掘算法GBMFI，并在两个标准数据集上对其进行测试，对最小支持度与最大频繁集的个数关系进行了研究。分别记录了算法的运行时间，最大频繁项集的个数以及不同长度下最大频繁项集的分布情况。与DepthProject进行了对比实验，结果表明该算法运行速度良好，尤其适用于稀疏数据集。下一步工作计划是针对大数据环境下的分布式存储机制，研究分布式并行的最大频繁项集挖掘算法。

[1]Wu X,Zhu X, Wu G Q,et al. Data mining with big data[J].IEEE Transactions on Knowledge and Data Engineering,2014,26(1):97-107.

[2]Agrawal R,Srikant R.Fast algorithms for mining association rules[C].Santiago: Proceedings of the 20th International Conference on Very Large Data Bases,2000.

[3]Han J, Pei J,Yin Y.Mining frequent patterns without candidate generation[C].Dallas:Proceeding of SIGMOD Conference,2000.

[4]Fournier-Viger P,Wu C W,Tseng V S.Mining maximal sequential patterns without candidate maintenance[M].Heidelberg: Advanced Data Mining and Applications Springer Berlin Heidelberg, 2013.

[5]蒋翠清,胡俊妍.基于FP-tree的最大频繁项集挖掘算法[J].合肥工业大学学报:自然科学版,2010,33(9):1387-1391.

[6]Huiling P,Yunxing S.A new FP-tree-based algorithm MMFI for mining the maximal frequent itemset[C].Ottawa: Computer Science and Automation Engineering (CSAE),2012.

[7]马丽生,姚光顺,杨传健.基于改进FP-tree的最大频繁项目集挖掘算法[J].计算机应用,2012,32(2):326-329.

[2]杨鹏坤,彭慧,周晓峰,等.改进的基于频繁模式树的最大频繁项集挖掘算法—FP-MFIA[J].计算机应用,2015,35(3):775-778.

[3]马志新,陈晓云,王雪,等.最大频繁项集挖掘中搜索空间的剪枝策略[J].清华大学学报:自然科学版,2005,45(S1):1748-1752.

[4]Agrawal R, Imielinski T, Swami A N. Mining association rules between sets of items in large databases[C].Washington,D.C:Proceeding of SIGMOD Conference,1993.

[5]Burdick D,Calimlim M,Gehrke J.MAFIA:A maximal frequent item set algorithm for transactional database[C].Heidelberg: Proceedings of the 17th Conference on Data Engineering,2001.

[6]Zaki M J. Scalable algorithms for association mining[J].IEEE Transactions on Knowledge and Data Engineering,2000,12(3):372-390.

[7]Jiawei Han, Micheling Kamber, Jian Pei .数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2012.

[8]Agarwal R C,Aggarwal C C,Prasad V V V. Depth first generation of long patterns[C].Boston:Proceeding of Sixth ACM SIGKDD International Conference, Knowledge Discovery and Data Ming,2000.

Mining Maximal Frequent Itemsets Based on Back Track

ZHANG Xinjing, YU Jiawei, WANG Hongmei

(School of Computer Science and Engineering, Changchun University of Technology, Changchun 130012, China)

In view of the fact that Apriori algorithms scans the database multiple times and the FP-tree algorithms requires build a large number of conditional trees, the GBMFI algorithm is proposed for mining maximal frequent itemsets. The transaction database is stored in vertical format. Based on the enumeration tree, the GBMFI algorithm performs the pruning operation to narrow the search space with the properties of non-frequent subsets and the support information of the node to get maximal frequent item sets. Experiments demonstrate the effectiveness of the GBMFI, especially for spares data sets.

data mining; maximal frequent item set; association rule; back track method; pruning

10.16180/j.cnki.issn1007-7820.2016.08.023

2015-11-24

国家自然科学基金资助项目(61133011)；吉林省教育厅“十二五”科学技术研究基金资助项目(2013431)

张心静(1990-)，女，硕士研究生。究方向：数据挖掘。于嘉威(1993-)，男，本科。研究方向：ACM程序设计竞赛。王红梅(1968-)，女，教授，硕士生导师。研究方向：数据挖掘等。

TP311

A

1007-7820(2016)08-078-04