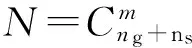基于多维空间的燃烧平衡产物组成的计算方法
2016-09-19何伟平刘晓静陈厚和
何伟平,黄 菊,刘晓静,陈厚和
(1.徐州工业职业技术学院化学工程技术学院,江苏 徐州 221140; 2.徐州工程学院化学化工学院,江苏 徐州 221111;3.南京理工大学化工学院,江苏 南京 210094)
基于多维空间的燃烧平衡产物组成的计算方法
何伟平1,黄菊2,刘晓静1,陈厚和3
(1.徐州工业职业技术学院化学工程技术学院,江苏 徐州 221140; 2.徐州工程学院化学化工学院,江苏 徐州 221111;3.南京理工大学化工学院,江苏 南京 210094)
为计算燃烧平衡产物的组成,在质量守恒关系的基础上,得到一系列基本可行解。根据吉布斯自由能,对基本可行解进行优化筛选,将筛选得到的基本可行解视为多维解空间的顶点,以吉布斯自由能降低为判据,利用基本可行解逐个与初始解线性组合,从而搜索得到最佳点,即为最终平衡产物组成。应用文献数据对计算结果的准确性进行验证。结果表明,该方法计算平衡产物的组成与文献数据基本一致,燃烧温度最大误差不超过3%。
燃烧;平衡产物;多维空间;搜索算法;最小自由能;吉布斯自由能
引 言
含能材料燃烧热力学计算的关键在于平衡产物的确定,确定平衡产物的基本方法有平衡常数法和最小自由能法。目前应用最多的是最小自由能法[1-3],其基本原理是:在给定的温度和压强下,体系的吉布斯自由能达到最小值时,混合体系的组成即为平衡组成。应用该原理求算平衡产物,其实质是在满足质量守恒的条件下,解决自由能最小的极值问题,一般通过引入拉格朗日因子来处理该问题[4],传统的计算机求解方式有泰勒展开法、Newton法、布罗依登法[5-7]等,但这些求解方式存在初始解设置难度大,计算复杂或收敛困难的问题。
针对传统求解方式存在的弊端,出现了一些新的解决办法,如借助惩罚函数法[8]、支持向量机方法[9]、随机方向法[10]、遗传算法[11]等进行不同程度的改进,这些方法较好地解决了传统求解方式的弊端。但也存在一些不足,如惩罚函数法的罚因子非常重要,然而较难设置合适的罚因子,并且罚因子每次迭代后,均需要重新求出最优解[8];支持向量机方法则由于涉及矩阵运算,当训练样本较多时会显著增加计算复杂度,并且预测精度也严重依赖于训练样本;随机方向法与遗传算法虽然具有良好的全局搜索能力,但其局部搜索能力较差,尤其在后期搜索效率较低,导致计算非常费时。本研究提出了一种基于多维空间的燃烧平衡产物的计算方法。其基本思路为:燃烧产物的所有可能解构成多维解空间(为凸空间,其维度即为产物种类数),平衡组分的最优解必然位于该解空间内的某点,而质量守恒方程组的基本可行解则可视为该解空间的顶点。由初始解出发,以吉布斯自由能下降为依据,向不同顶点所在的方位进行搜索,则将收敛于吉布斯自由能最低点,即平衡组分的最优解,为降低计算复杂程度、提高计算效率并保证计算精度等提供一种新方法。
1 求解方法
1.1数学模型的建立
燃烧平衡产物的求解模型满足质量守恒、反应前后总焓相等以及产物吉布斯自由能最小等条件。其数学模型可表示如下:
(1)
式中:T为燃烧温度;G为体系的吉布斯自由能;Hi为第i种产物的摩尔焓;Si为第i种产物的摩尔熵;ng为气态产物种数;ns为凝聚态产物种数;aij为第i种产物分子式中的第j种元素原子的个数;xi为第i种产物的摩尔数;bj为第j种元素的总摩尔数;m为体系的元素种数;H0为含能材料的生成焓。
1.2基本可行解的筛选
平衡产物的任意一组解Xi=(x1,x2,…,xng,…,xng+ns)T均可表示为(ng+ns)维空间中的一点,并应满足xi≥0 (i=1,2,…,ng,…,ng+ns)。
实际上满足式(2)的基本可行解的组合情形往往很多,故应筛选出对后面搜索最为有利的组合情形。因为吉布斯自由能是连续函数,故最有利情形是指:式(1)的最优解与式(2)所表示的向量的吉布斯自由能最为接近,这样初始解经过若干次搜索并修正后最容易收敛到最优解上。考虑到通常在假定温度(如3000K)并在定压条件(如30MPa)下求解平衡产物,故采取以下方式进行筛选:
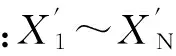

图1 基本可行解的筛选流程Fig.1 Screening process of basic feasible solutions
计算表明,由于基本可行解之间的差异较大,在温度、压强变化不是特别显著的情形下,筛选出的X″1~X″ng+ns不会发生明显变化。故定压条件下,分别计算温度区间[T1,T2]两个端点T1、T2的X″1~X″ng+ns,若无明显差异(例如差异的个数少于n),则认为以其中一组X″1~X″ng+ns代替区间上各点的筛选结果,不会影响燃烧产物的搜索结果。
1.3搜索方法
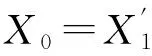
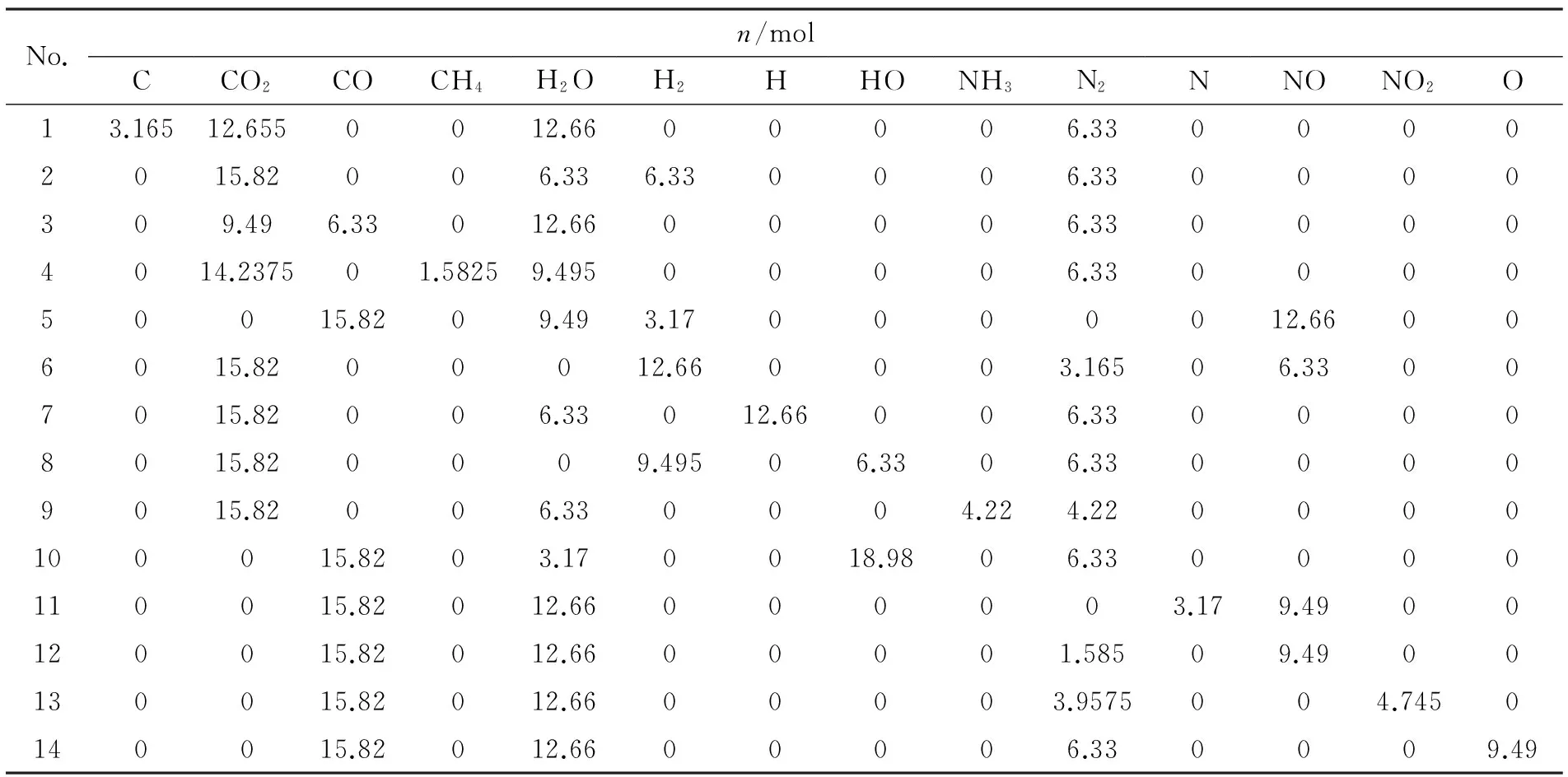
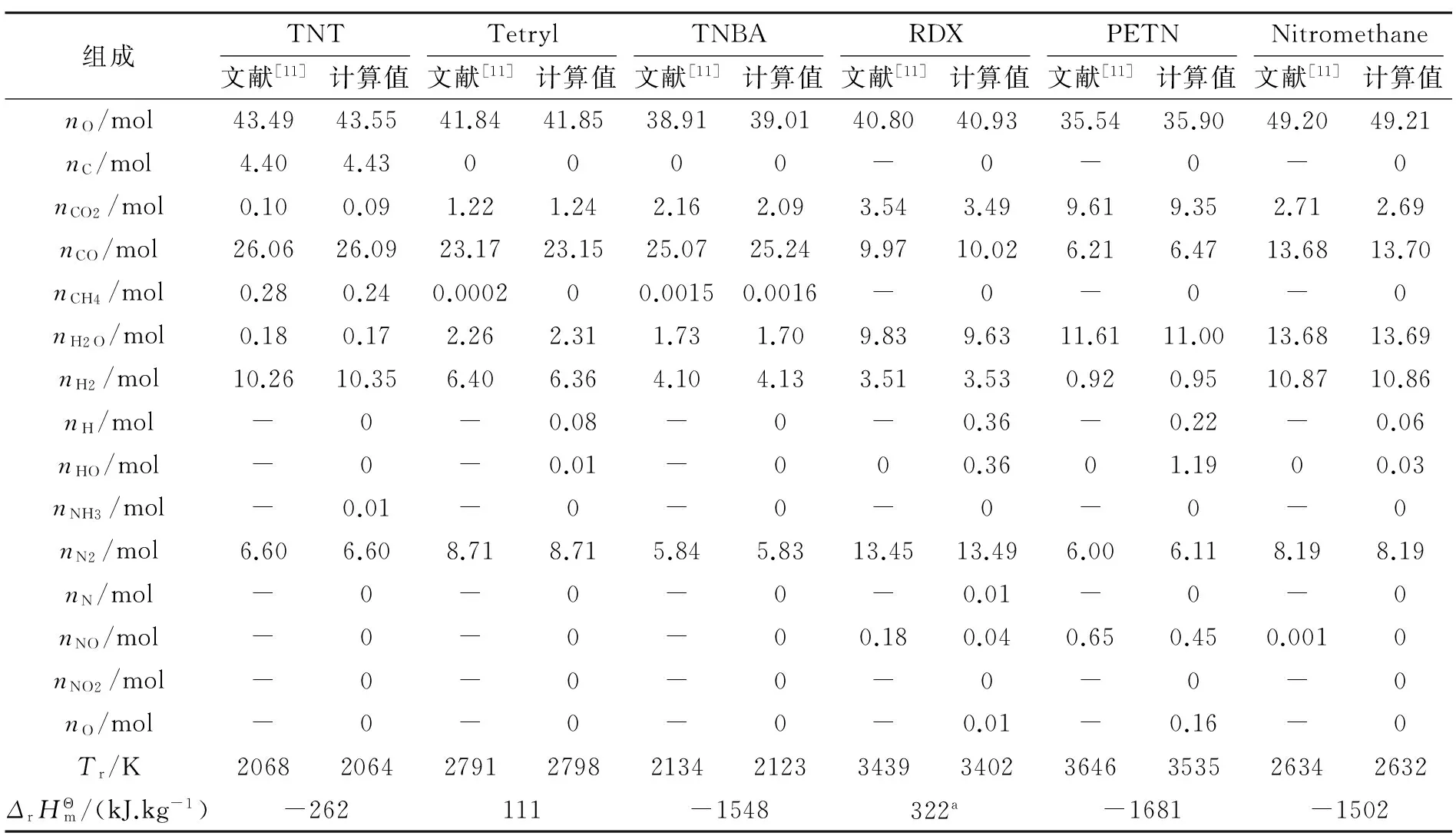
(1)给定温度和压强,计算XT1=(1-r)X0+rX″1,若吉布斯自由能G(XT1) (2)利用余下的X″2~X″ng+ns,依次对X0重复以上操作; (3)重复(1)、(2)操作,直至X0不再被更新,转向(4); (4)令r=0.5r,继续(1)~(3)的搜索操作,直至r 图2 平衡组分搜索过程示意图Fig.2 Schematic diagram of search process for equilibrium compositions 根据以上求解方法,利用Visual Basic 6.0语言编写燃烧平衡产物搜索的程序代码。为了验证本方法的可行性和准确性,选取文献[11]讨论的14种燃烧产物进行研究,结合不同含能材料的元素组成,进行基本可行解的筛选,并在此基础上进行计算。以PETN为例,在T=3000K,p=30MPa时筛选的基本可行解如表1所示(基本可行解总数N=163),产物统计以1kg含能材料参与计算为基准。 采用本方法计算结果与文献[13]中采用遗传算法的计算结果进行对比,结果如表2所示,其中燃烧产物压强为30MPa。 表1 基本可行解筛选结果 表2 燃烧产物计算结果 从表2可以看出,采用基于多维空间的燃烧平衡产物的计算方法,得到的结果与文献[11]采用遗传算法计算的结果基本一致,差异稍大的为PETN,其次为RDX,但燃烧温度误差均不超过3%。分析文献[11]的产物数据可以发现,由于PETN及RDX存在较多的次要产物可能未被考虑(即表中标记为“-”的位置,其总数量分别为0.54mol、0.32mol),故引起结果与本研究不一致。文献[13]采用平衡常数法计算PETN的燃烧产物组成(mol):nO=36.06,nCO2=8.87,nCO=6.95,nH2O=11.04,nH2=1.04,nHO=0.96,nN2=6.17,nNO=0.32,燃烧温度Tr=3473K;RDX的燃烧产物组成(mol):n0=40.91,nCO2=3.37,nCO=10.12,nH2O=9.62,nH2=3.54,nHO=0.36,nN2=13.46,nNO=0.1,燃烧温度Tr=3375K。可见采用本方法的计算结果大体上介于文献[11]和文献[13]结果之间,因此具有较好的可信性。 搜索各平衡产物过程中,r和T的总更新次数分别为:TNT(377,14)、Tetryl(465,14)、TNBA(874,14)、RDX(2114,15)、PETN(278,15)、Nitromethane(454,14),括号中的第1个数值为r的总更新次数,第2个数值为T的总更新次数。除RDX外,其他含能材料燃烧平衡产物的搜索,r的更新次数在200~900之间。在Intel core i5处理器下,程序计算TNT、Tetryl、TNBA、RDX、PETN、Nitromethane所需要的时间分别为469、1078、1500、3282、750、1343ms。可见利用本计算方法,程序在经过搜索步数不是很大的情形下,就能快速找出符合精度要求的最优解。 (2)在给定温度和压强下,对基本可行解进行筛选,可有效提高程序搜索效率和预测精度。可以预见,该处理方式同样适用于采取其他方法求解燃烧平衡产物的过程。 (3)不同于传统方法将质量守恒约束方程与目标函数通过拉格朗日因子组合到一起,本方法将最优解表示为约束方程可行解的线性组合,简化了求解过程,同时保证了产物的计算精度;并通过优化求解过程,保证了计算效率。 [1]Gordon S,McBride B J. Computer program for calculation of chemical equilibrium compositions and applications:I Analysis,NASA RP-1311[R].Washington D C:NASA,1994. [2]McBride B J,Gordon S. Computer program for calculation of chemical equilibrium compositions and applications:Ⅱ Users manual and program description,NASA RP-1311[R]. Washington D C:NASA,1996. [3]李猛,赵凤起,徐司雨,等. 三种能量计算程序在推进剂配方设计中的比较[J]. 火炸药学报,2013,36(3): 73-77. LI Meng,ZHAO Feng-qi,XU Si-yu,et al. Comparison of three kinds of energy calculation programs in formulation design of solid propellants[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2013,36(3): 73-77. [4]潘功配,杨硕. 烟火学[M].北京:北京理工大学出版社,1997:42-52. [5]田德余. 气态物系平衡组成的计算[J]. 计算机与应用化学, 1986,3(4):310-313. Tian De-yu. The computation of chemical equilibrium composition in gaseous systems[J]. Computers and Applied Chemistry, 1986,3(4):310-313. [6]宋东明,潘功配,王乃岩. 基于最小自由能法的烟火药燃烧产物预测模型[J]. 弹箭与制导学报,2006,26(1):120-122. SONG Dong-ming,PAN Gong-pei,WANG Nai-yan. Calculation model of pyrotechnical combustion products based on Minimum free-energy[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(1):120-122. [7]王雪,潘功配,李毅. 最小自由能法烟火剂平衡产物计算[J]. 火炸药学报,1994,22(4):61-63. WANG Xue,PAN Gong-pei,LI Yi. Calculation of pyrotechnic composition equilibrium products based on principle of free-energy minimization[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),1994,22(4):61-63. [8]许小平,张唯. 惩罚函数法计算燃烧产物的平衡组成[J]. 宇航学报,1994(3):90-95. XU Xiao-ping,ZHANG Wei. Calculation of equilibrium composition of combustion products by penalty method[J]. Journal of Astronautics,1994(3):90-95. [9]范磊,潘功配,欧阳的华,等. 基于支持向量机的Mg/PTFE烟火药燃烧特性预测[J].含能材料,2012,20(4):414-417. FAN Lei,PAN Gong-pei,OUYANG De-hua,et al. Combustion characteristics forecast of Mg/PTFE pyrotechnic composition with support vector machine[J]. Chinese Journal of Energetic Materials,2012,20(4):414-417. [10] 菅晓霞,刘庆上,邹伟伟,等. 随机方向法赋初值求火药燃烧产物的平衡组成[J].含能材料,2012,20(2):202-204. JIAN Xiao-xia,LIU Qing-shang,ZHOU Wei-wei,et al. Calculation of equilibriun composition of combustion products of gunpowder based on random direction method initialization[J]. Chinese Journal of Energetic Materials,2012,20(2):202-204. [11] 谢中元,周霖,王浩,等. 遗传算法在燃烧产物平衡组分计算中的应用[J].含能材料,2015,23(4):340-345. XIE Zhong-yuan,ZHOU Lin,WANG Hao,et al. Application of genetic algorithm in calculation of combustion equilibriunm composition[J]. Chinese Journal of Energetic Materials,2015,23(4):340-345. [12] Kubota, Naminosuke. Propellants and Explosives: Thermochemical Aspects of Combustion[M].Hoboken:John Wiley & Sons, 2015: 23-29, 64-65. [13] 周霖. 爆炸化学基础[M].北京:国防工业出版社,2005:33-37. Calculation Method of Combustion Equilibrium Product Compositions Based on Multidimensional Space HE Wei-ping1, HUANG Ju2, LIU Xiao-jing1, CHEN Hou-he3 (1.School of Chemical Engineering, Xuzhou College of Industrial Technology,Xuzhou Jiangsu 221140, China;2.School of Chemistry & Chemical Engineering, Xuzhou Institute of Technology, Xuzhou Jiangsu 221111, China;3.School of Chemical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China) To calculate the combustion equilibrium product compositions, a series of basic feasible solutions were obtained on the basis of conservation of mass. According to Gibbs free energy, the basic feasible solutions were optimized and selected. The basic feasible solutions obtained by selecting were considered as the vertex of the multidimensional space, the decrease of Gibbs free energy was considered as the criterion, the best point was obtained via search using linear combination one by one of basic feasible solution and initial solution, namely the final equilibrium product compositions were obtained. The accuracy of the calculation results was verified by the literature data. Results show that the compositions of equilibrium product calculated by this method are in agreement with the literature data, and the maximum error of combustion temperature is no more than 3%. combustion;equilibrium product;multidimensional space; search algorithm;minimum free energy;Gibbs free energy 10.14077/j.issn.1007-7812.2016.04.009 2016-03-18; 2016-04-28 徐州市科技计划社会发展项目(KC15SH064);徐州工业职业技术学院科技基金资助项目(XGY201409) 何伟平(1983-),男,硕士,讲师,从事含能材料理论计算研究。E-mail:252927740@qq.com TJ55;O643.2+1 A 1007-7812(2016)04-0046-05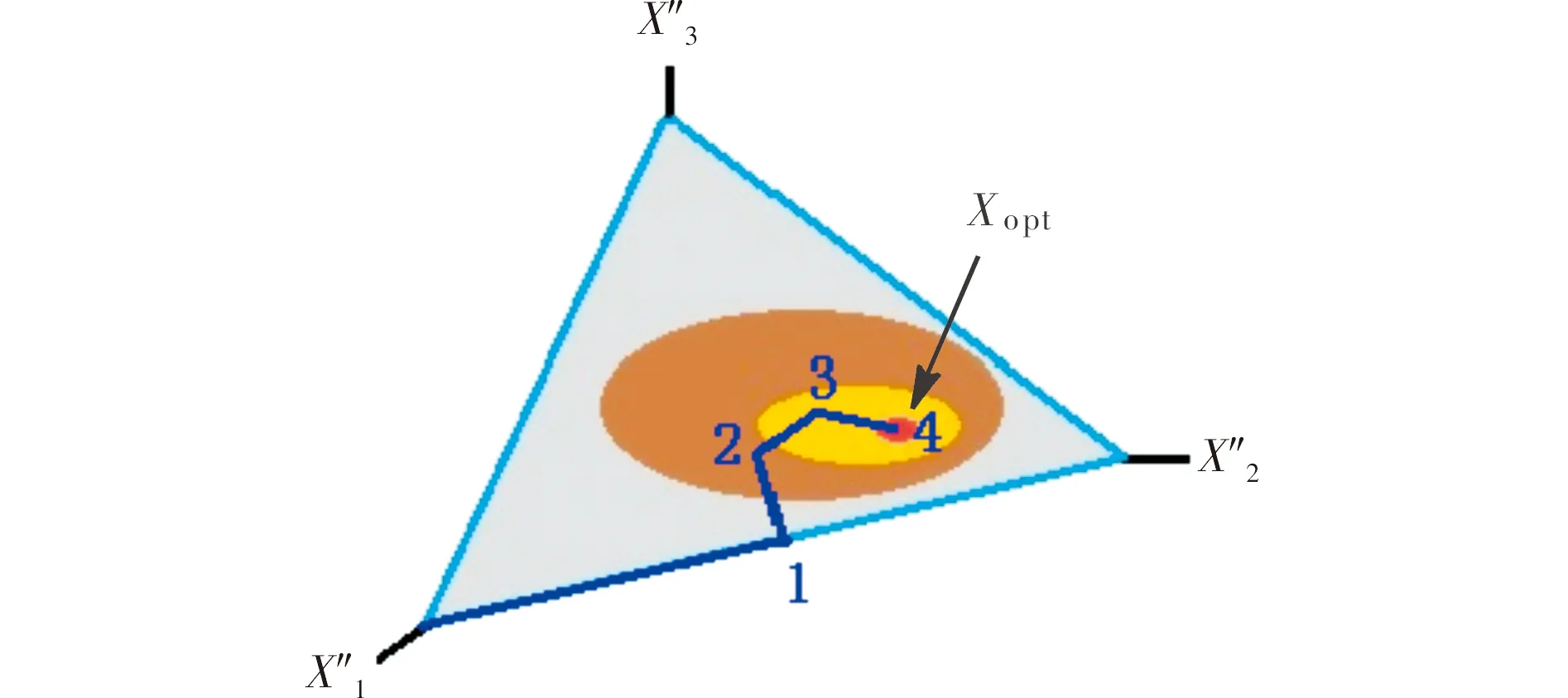
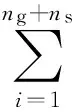
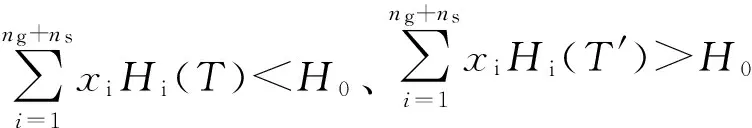
2 计算验证
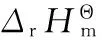
3 结 论