杨氏模量实验中长度测量仪器的选配

吕兆承

(淮南师范学院　物理与电子信息系，安徽　淮南　232000)



杨氏模量实验中长度测量仪器的选配

吕兆承

(淮南师范学院物理与电子信息系，安徽淮南232000)

合理选择和搭配仪器是设计性实验的一个关键内容。文中以静态拉伸法测量金属丝杨氏模量实验为例，从测量不确定度角度出发，按照不确定度均匀分配原则，把间接测量量的不确定度要求转变为对各个直接测量量的不确定度的估算，以此选择满足要求的测量仪器，为设计性实验提供一种简单的获得仪器选配的定量指导。

杨氏模量；测量仪器；选配；不确定度

在物理实验测量中，一般对实验结果都会提出不确定度的要求和期望。所以指定实验方案时，必须考虑所采用的仪器、方法以及数据处理是否能满足最终结果的不确定度要求，其中仪器的选配尤为重要。仪器选择要从仪器分配率、精确度和量程几个方面来考虑，原则是方便、经济、安全，只要能够达到规定的测量准确度即可。如果实验比较复杂，还会涉及到多种测量仪器测量多个物理量，因此要考虑仪器的配套问题[1]。

杨氏模量是工程材料的重要参数，反映了材料弹性形变与内应力的关系，它只与材料性质有关，是选择工程材料的重要依据之一。传统的静态拉伸法测杨氏模量的方法从杨氏模量本身的定义出发，实验原理简单、直观、易于理解[2-4]。它涉及4种不同的典型长度测量，而常用的长度测量仪器有钢卷尺、米尺、游标卡尺、螺旋测微器和移测显微镜，即同一物理实验量的测量有多种测量仪器可供选择。本文借助间接测量的不确定度传递公式，主要研究如何合理选择和搭配仪器问题，以期对设计性实验教学提供一定的参考。

1　实验仪器

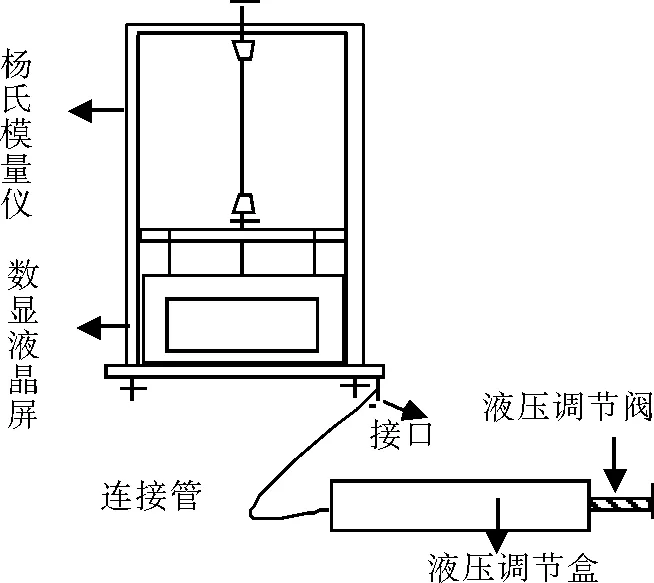
图1　数显液压加力杨氏模量拉伸仪

本实验的整套装置由“数显液压加力杨氏模量拉伸仪”和“新型光杠杠”组成。数显液压加力杨氏模量拉伸仪如图1所示，金属丝上下两端用钻头夹具夹紧，上端固定于双立柱的横梁上，下端钻头卡的连接拉杆穿过固定平台中间的套孔与拉力传感器相连。加力装置施力给传感器，从而拉伸金属丝。所施力大小F=mg由电子数字显示系统显示在液晶显示屏上，加力大小由液压调节阀改变。

图2(a)为新型光杠杆的结构示意图，在等腰三角形铁板1的三个角上，各有一个尖头螺钉，底边连线上的两个螺钉B和C称为前足尖，顶点上的螺钉A称为后足尖；2为光杠杆倾角调节架，其中b为光杠杆后足尖A到两前足尖B、C连线的垂直距离，被称为光杠杆常数，如图2(b)所示；3为光杠杆反射镜。

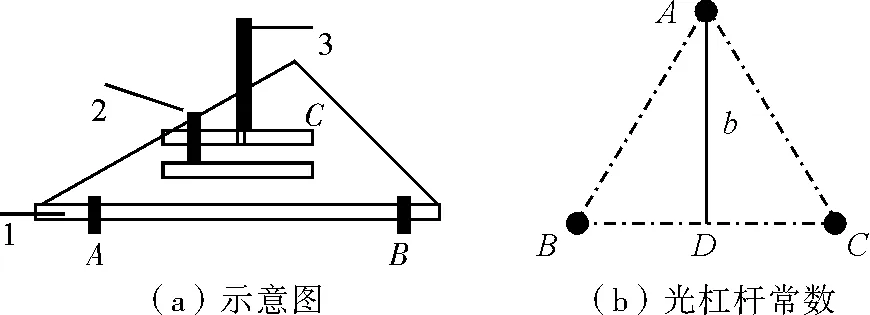
图2　新型光杠杆

2　实验原理

设长为L，截面积为S的均匀金属丝，在两端以外力F相拉后，伸长ΔL。实验表明，在弹性范围内，单位面积上的垂直作用力F/S(正应力)与金属丝的相对伸长ΔL/L(线应变)成正比，其比例系数就称为杨氏模量即：

(1)

式中，F、L和S都易于测量，ΔL属微小变量，直接测量金属丝微小的长度变化非常困难，因此使用光杠杆方法来测量，原理如图3所示。当光杠杆反射镜的后足尖下降ΔL时，产生一个微小偏转角θ，在望远镜上读到的标尺读数变化P1-P0即为放大后的钢丝伸长量N，常称作视伸长。由图3可知：

ΔL=btanθ≈bθ

(2)

N=P1-P0=Dtan4θ≈4Dθ

(3)

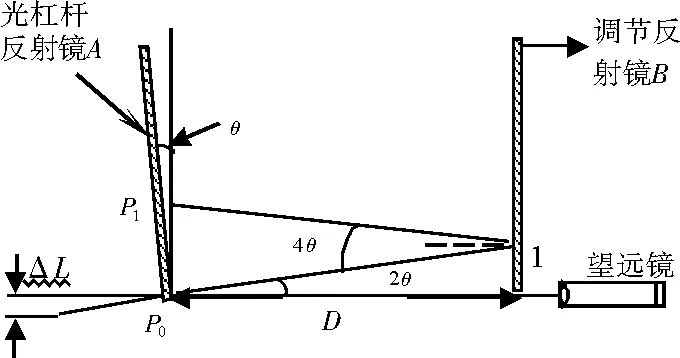
图3　光杠杆放大原理示意图

那么，金属丝的杨氏模量可以表示为：

(4)

3　杨氏模量不确定度分析和仪器选择

实验中，杨氏模量相对不确定度传递公式为：

(5)

由式(5)可知，杨氏模量的相对不确定度分别由施力大小mg、金属丝长度L、光杠杆反射镜镜和调节反射镜间距离D、金属丝直径d、光杠杆常数b及标尺读数的变化N的相对不确定度决定。

(6)

由此可得：

uC(m)≤0.02m；uC(L)≤0.02L；uC(D)≤0.02D；uC(d)≤0.01d；uC(b)≤0.02b；

uC(N)≤0.02N。

则问题由最终不确定度要求转变为各个直接测量量的不确定度估算。但由不确定度的特性可知，每个直接测量量的不确定度又分为A类分量和B类分量，其中A类分量由统计方法计算获得，不能事先求得。而B类分量是非统计方法计算的误差分量，一般可分为两种情况:一是由测量仪器的误差限Δ仪来表示；另一种为测量的估计误差Δ估。但在一般情况中，Δ仪比Δ估大得多，所以Δ仪将作为测量结果的B类不确定度分量，可表示为uB=Δ仪/C(P=0.683)，其中C为置信系数，与误差分布形式有关，P为置信概率。目前，人们对许多仪器在测量过程中误差分布性质尚不完全清楚，为了使问题简化，当置信概率P为1时，uB=Δ仪。因此估算时，每个直接测量量的不确定度可直接取为测量仪器的误差限：

uC=uB=Δ仪

(7)

式中，Δ仪在仪器说明书上直接标出，如果未注明仪器误差或不清楚的：对于能连续读数(能对最小分度下一位进行估计)的仪器，取最小分度值的一半作为仪器误差，如米尺、螺旋测微器等；对于不能连续读数的仪器就以最小分度值作为仪器误差，如游标类仪器、数字式仪表等。

考虑到测量实验条件受限制，测量金属丝长度L和光杠杆反射镜到调节反射镜间的距离D时，由于实验装置的原因，很难将被测物两端与刻度尺的刻度线对齐，以及钢卷尺弯曲、不水平等因素的影响，选用钢卷尺测量L和D，取其误差限分别为3 mm和5 mm。其他仪器的误差限由仪器说明书上直接得到，见表1。这里选择测量仪器的具体要求是:实验所用测量仪器的误差限不大于实验对测量不确定度的要求。在满足该原则的条件下，尽量选择精度较低且操作方便的仪器[5]。因此，实验中用3 m钢卷尺测量L和D，150 mm钢板尺测量b，螺旋测微器测量d，N是由微小长度变化通过光杠杆发大以后在望远镜中测量。

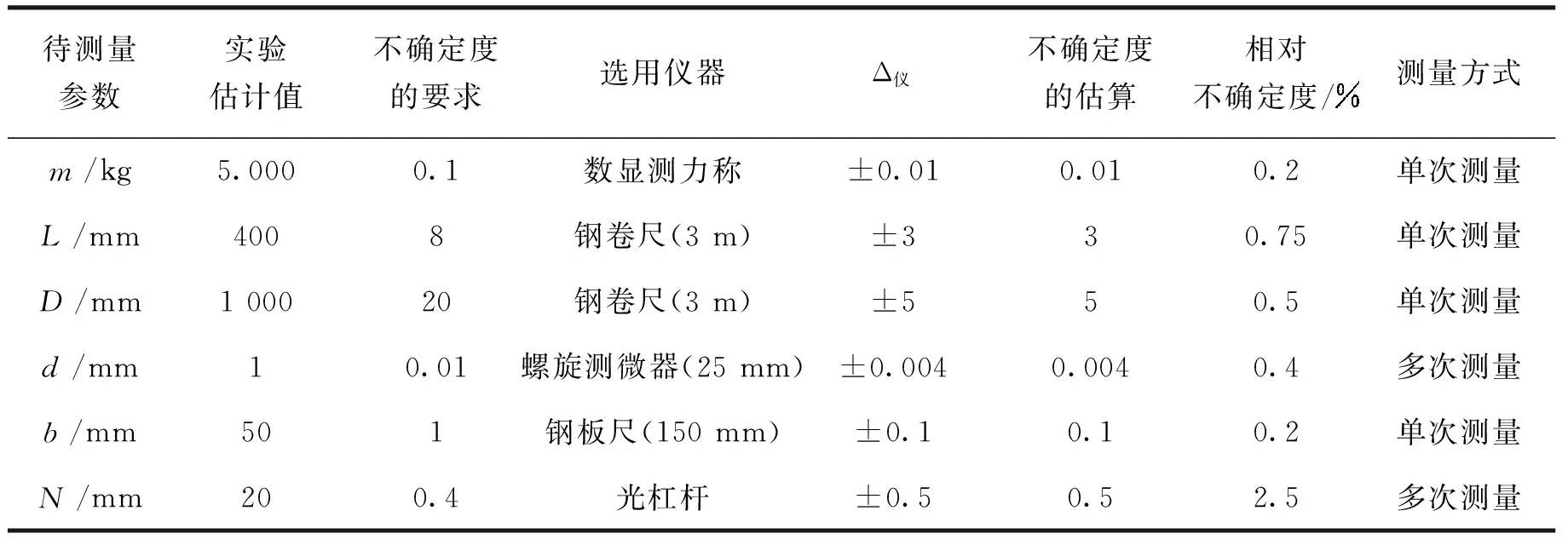
表1　各直接待测量与选用仪器

在上述仪器选择中，L和D误差限估算的不确定度远小于其要求的不确定度，且其相对不确定度传递系数为1，可能引入的偶然误差较小，故分别用钢卷尺一次测量。同理，b用钢板尺单次测得。金属丝直径d估算的不确定度为±0.004 mm，其不确定度传递系数为2，明显大于其他量的不确定度传递系数，故选择准确度等级最高的螺旋测微器测量。螺旋测微器测量精度较高，可能引入的误差较大，同时金属丝粗细不均匀会导致随机变化的系统误差，故对d测量时选择在金属丝不同的部位及不同方位进行多次测量。除了N的不确定度略大于要求外，其他量均远小于要求的不确定度，这样最终结果的相对不确定度可以满足要求。N是由微小长度变化通过光杠杆发大以后在望远镜中测量的，可能引入较大的偶然误差，同时考虑到不同的负载求平均，以及加载和减载时由摩擦和弛豫效应引入的系统误差，所以N的测量采用上行、下行加载进行，并用逐差法处理数据，使整个测量更加合理。

4　实验数据处理与结果

1)L、D和b单次测量。

其测量结果分别是:

L=(38.2±0.2)10-2m；D=(104.2±0.3)10-2m，b=(4.60±0.01)10-2m

2)金属丝直径d的测量。

金属丝直径d的测量结果见表2。由表2可得，金属丝直径d=(0.800±0.002)×10-3m。

表2　金属丝直径d测量(零点读数:0.006 mm)

3)光杠杆测量N。

光杠杆测量N结果见表3。由表3可得，

N=(1.88±0.03)10-2m。

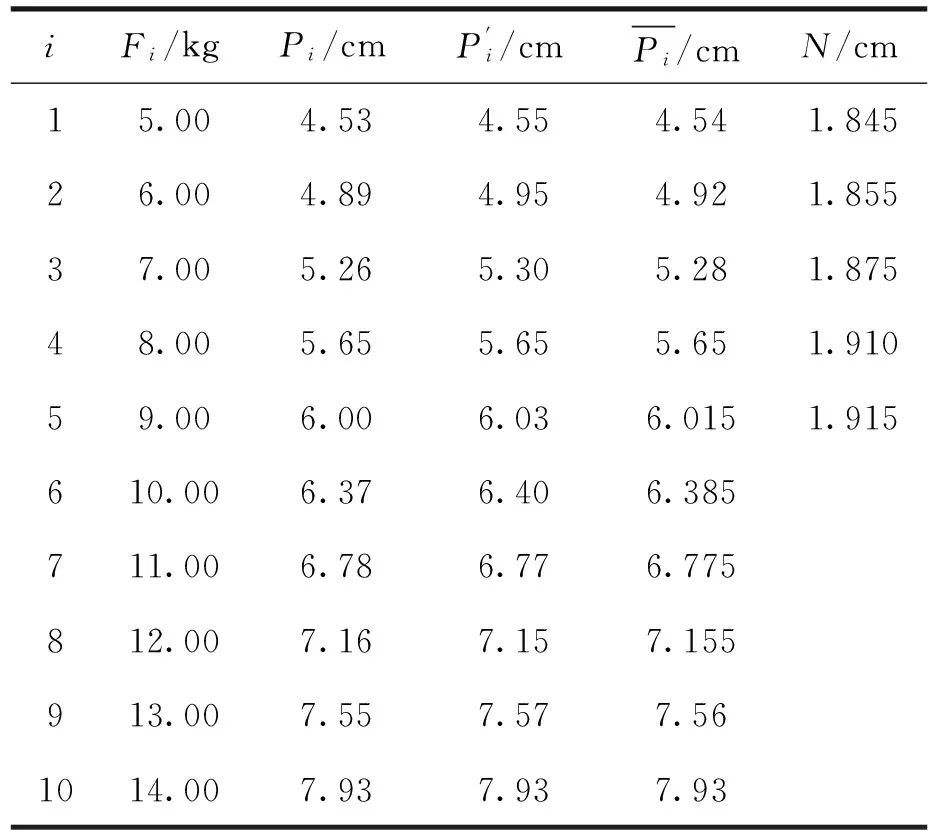
表3　光杠杆测量(N=Pi+5-Pi)

根据式(4)和式(5)可得，金属丝杨氏模量的最终测量结果为：

5　结束语

通过以上的分析和计算，间接测量量的不确定度传递公式除了用来估算间接测量值的不确定度之外，还可以用来分析各直接测量值的不确定度对间接测量结果不确定度影响的大小，为合理选择测量仪器和实验方法提供依据。在实际测量中选择和搭配仪器时，不能认为仪器的精度越高越好，因为精度高的仪器调节复杂，容易受外界干扰，并且价格昂贵，应考虑实际条件。对测量结果影响较大的物理量，应采用精度较高的仪器；而对测量结果影响不大的物理量，就不必追求高精度仪器，使测量方便、经济、安全[7]。

[1]陈水桥，王鲲，陈洪山.浅谈如何合理性选配和组建物理实验仪器系统[J].物理实验，2006，26(8):16-19.

[2]李恩普.大学物理实验[M].北京:国防工业出版社，2004:38-42.

[3]车东伟，姜山，张汉武，等.静态拉伸法测金属丝杨氏模量实验探究[J].大学物理实验，2013，26(2):33-34.

[4]周晓明.三种杨氏模量测量方法比较[J].实验科学与技术，2011，9(6):97-99.

[5]张小娣，牛超英，张辉.基于不确定度理论的物理实验设计[J].咸阳师范学院学报，2010，25(4):27-29.

[6]李远兴，申冬玲.杨氏模量实验的不确定度评定[J].四川兵工学报，2009，30(7):137-138.

[7]田真.不确定度与测量仪器及测量方案的选择[J].暨南大学学报，2000，21(5):49-50.

Research on Selecting the Length Measuring Instruments for Young’s Modulus

LÜ Zhaocheng

(Physics and Electronic Information Engineering，Huainai Normal University，Huainan 232000，China)

The rational selecting of measuring instruments is one of key elements during designing experiments.This paper discusses the measuring Young’s modulus of tinsel by pulling and stretching method from the perspective of measurement uncertainty，introducing a method of transforming the requirement of the indirect measurement uncertainty into the estimation of the uncertainty of direct measurements by the uniform distribution of the uncertainty principle，which is expected to provide a reference to design experiments to meet the requirements of measuring instruments.

Young’s modulus；measuring instruments；selection；uncertainty

2014-10-23

淮南师范学院校级质量工程项目(2014hsjyxm36)。

吕兆承(1983-)，男，硕士，助理实验师，主要从事大学物理实验教学和研究工作。

O4-33;G484

A

10.3969/j.issn.1672-4550.2016.01.008