基于ElGamal体制的无需配对无证书签名方案

彭　程，杨邓奇

(1.云南大学 数学与统计学院，昆明　650091；2.大理学院 数学与计算机学院，云南　大理　671003)



基于ElGamal体制的无需配对无证书签名方案

彭程1，杨邓奇2

(1.云南大学 数学与统计学院，昆明650091；2.大理学院 数学与计算机学院，云南大理671003)

ElGamal签名体制；无证书签名；无双线性对

签名是网络系统安全的必要元素，目前的签名技术如RSA、ECDSA等在实现公钥管理时主要是基于PKI技术；然而，基于PKI技术的公钥管理需要复杂的证书管理，系统实现比较复杂。2001年，文献[1]提出基于身份的密码系统(IBC)，旨在消除传统公钥证书密码体制中烦琐的公钥管理过程。但是基于身份的密码系统存在密钥托管问题。文献[2]提出了无证书公钥密码系统(CL-PKC)以解决基于身份密码系统中的密钥托管问题，同时去除传统公钥证书体制中烦琐的证书管理过程，并提出了无证书密码系统基于双线对。双线性对的运算是比较耗时的运算，文献[3]指出，进行一次双线性对运算、指数运算和哈希运算所需的计算量分别至少是椭圆曲线标量乘法的21倍、3倍和1倍。文献[4]首次提出无需配对的无证书密码系统，该系统存在大量的指数运算，并给出了一个无证书加密方案，没有给出相应的签名方案。2006-2011年期间，提出了诸多无证书签名方案及其变体[5-10]，但这些方案都需要进行多次双线性对的运算。2012年，文献[11]提出无双线性对的无证书签名方案，该方案在签名和验证阶段都不需要双线性对运算，其主要运算为椭圆曲线上的标量乘法(后文简称标量乘法)，具有较高的计算效率。但该方案用户密钥生成阶段存在一个问题，即在用户获得由KGC为其提供的部分私钥后，可以恶意地选择多个秘密值进行计算，使一个部分私钥对应多个秘密值，即一个用户、一个部分私钥对应多个公私钥对，这对系统安全造成了严重威胁。此外，该方案在验证的效率并不是只需2次标量惩罚和1次哈希运算，而是需要4次标量乘法和1次哈希运算。

1　预备知识

1.1困难问题及假设

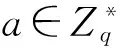
1.2通用的无证书签名方案

一般来讲，无论是基于双线性对还是无需配对的无证书签名方案，通常包括7个算法[2]。

1)系统初始化算法:由KGC执行，输入安全参数k，输出系统主密钥s和参数Params，其中主密钥s由KGC保密，而参数Params公开。

2)用户秘密值生成算法:在用户端执行，输入系统参数Params和用户ID，输出用户秘密值xID和对应的公开值XID。

3)用户部分密钥生成算法:在KGC上执行，输入系统参数Params、系统主密钥s、用户身份(ID)和公开值XID，输出用户部分私钥DID和对应的部分公钥PID。

4)用户私钥生成算法:在用户端运行，输入系统参数Params、用户部分密钥DID和用户秘密值xID，输出用户私钥SKID。

5)用户公钥生成算法:在用户端运行，输入系统参数Params、公开值XID和用户部分公钥PID，输出用户公钥PKID。

6)签名算法:由签名用户运行，输入系统参数Params、用户私钥SKID、用户ID和消息M，输出消息M的签名。

7)验证算法:由验证用户运行，输入系统参数Params、用户公钥PKID、用户ID和签名。若验证通过，输出1；否则，输出0。

1.3安全模型

无证书密码系统考虑两类攻击者[2]，令AI和AII分别表示第一类攻击者和第二类攻击者。AI可以任意替换合法用户的公钥，但不能查询系统主密钥。AII可以访问主密钥，但不能替换目标用户公钥。假设C是挑战者，AI为第一类攻击者，AII是第二类攻击者，则无证书签名方案的安全性可以用攻击者AI和AII与挑战者C之间交互的两个游戏来定义[2](两个游戏中，挑战者存储所有的查询历史)。

1.3.1定义1 游戏一(第一类攻击者与挑战者之间的交互)

Phase I-1:挑战者C运行Setup()建立系统参数，包括需要保密的主密钥s和公开参数params={p，q，G，P，P0，H1，H2}。

PhaseI-2:AI可以向挑战者C发出一系列以下查询:

Hash查询:AI选择一字符串，C返回该字符串的Hash值给AI。

部分私钥查询:AI选择一个用户ID，C根据系统参数及部分密钥生成算法，计算ID对应的部分私钥DID，并返回给AI。

秘密值查询:AI选择一个用户ID，C根据系统参数及秘密值生成算法，计算ID对应的秘密值xID，并返回给AI。

公钥查询:AI选择一个用户ID，C根据系统参数及公钥生成算法，计算ID对应的公钥PKID，并返回给AI。

签名查询:AI选择用户ID和消息m发送给C，C计算用户ID的私钥SKID，并用SKID该私钥对消息m进行签名，生成Sign(ID，m，SKID)并将其返回给AI。

签名验证查询:AI发送Sign(ID，m，PKID，result)给C，C验证签名有效性，若签名有效，则设置result=1；否则，设置result=0，并返回result值给AI。

PhaseI-3:AI伪造一个签名，输出四元组(m*，s*，ID*，PK*)，称AI在游戏中获胜，当且仅当:

1)s*是关于ID*、PK*和m*的一个有效签名；

2)AI从未执行过身份为ID*用户的部分私钥查询；

3)AI从未执行过关于ID*、PK*和m*的签名查询。

1.3.2定义2 游戏二(第二类攻击者与挑战者C之间的交互)

Phase I-1:挑战者C运行Setup()建立系统参数，包括需要保密的主密钥s和公开参数params={p，q，G，P，P0，H1，H2}。

Phase I-2:AII可以向挑战者C发出定义1中Phase I-2所定义的查询。

Phase I-3:AII伪造一个签名，输出四元组(m*，s*，ID*，PK*)，称AII在游戏中获胜，当且仅当:

1)s*是关于ID*、PK*和m*的一个有效签名；

2)AII从未执行过身份为ID*用户的秘密值查询或公钥替换查询；

3)AII从未执行过关于ID*、PK*和m*的签名查询。

1.3.3定义3(适应性选择消息攻击不可伪造性)

一个无证书签名方案在适应性选择消息攻击下是不可伪造的，当且仅当，任何多项式时间受限攻击者不能以不可忽略的优势赢得上述两个游戏。

本文中，安全的签名方案指签名方案在适应性选择消息攻击下存在不可伪造性。

2　无需配对的无证书签名方案

本论文基于ElGamal签名体制和无证书签名方案[4，11]，设计无需配对的无证书签名方案如下:

2.1系统参数建立

KGC生成两个素数p、q，使得q|p-1，P为安全椭圆曲线上循环加法群G中一个阶为q的生成元，选择Hash函数H1:{0，1}*×G×G|→Zq*。KGC选择主密钥s∈Zq*，并计算系统公钥P0=sP，公开系统参数params={p，q，G，P，P0，H1，H2}，保密主密钥s。

2.2用户秘密值生成

用户IDi随机选择xi∈Zq*作为其长期私钥，并计算Xi=xiP，将Xi发给KGC。

2.3用户部分私钥生成

KGC收到用户IDi发送的Xi后，随机选择一个ri∈Zq*，计算IDi的部分公钥Ri=riP，计算IDi的部分私钥Di=ri+sH1(IDi，Ri，Xi)，通过安全信道将Di返回给用户IDi。

2.4用户密钥生成

用户IDi收到Di后，通过计算判断等式Ri+H1(IDi，Ri，Xi)P0=DiP是否成立来判断KGC分配给自己的部分私钥是否有效。若有效，则用户IDi设置自己的私钥为SKIDi=〈xi，Di〉，公钥为PKIDi=〈Xi，Ri〉。

2.5签名过程

用户IDi随机选取αZq*且α0，计算Ti=αP，γ=H1(IDi，Ti，Xi)，e=SHA-x(m)，σ=(e+γxi+γDi)/α，生成签名(σ，γ)并发送给节点A。

2.6验证过程

当收到(σ，γ)后，节点A计算，h1=H1(IDi，Ri，Xi)，e=SHA-x(m)，u1=e/σ，u2=γ/σ，Q=u1P+u2(Ri+Xi+h1P0) ，并验证H1=(IDi，Q，Xi)=γ是否成立，若成立，输出1；否则输出0。

验证过程正确性:

所以H1(IDi，Q，Xi)=H1(IDi，Ti，Xi)=γ

3　安全与效率

3.1安全性分析

3.1.1密钥生成阶段的安全性

首先，本文所提的方案中，不存在文献[11]中一个部分私钥可以对应多个公私钥对的问题。因为，KGC在为用户生成其部分私钥之前，用户先选择秘密值xA，并将其对应的XA发送给KGC，由KGC负责将XA、部分公钥RA及IDA绑定。因此，有效地防止文献[11]中用户A通过生成多个XA来生成多个PK=〈XA，RA〉及SK=〈xA，rA〉的情况。

3.1.2签名方案安全性证明

本节对本文所提的签名方案的安全性进行证明。

定理1(无证书签名方案在AI攻击下存在不可伪造性):在随机预言模型(ROM)中，若群G上的离散对数问题(DL)是困难的，那么上述的无证书签名方案在敌手AI的攻击下是安全的。

证明:假设C想解决G上的DL问题，其DL问题的输入为(dP，P)，其目标是计算出d。假设AI能以不可忽略的优势攻破我们的签名方案，下面利用AI来解决群G上的DL问题。首先，C设置P0=dP，生成系统参数params={p，q，P，P0，H1，H2}并将其发给AI。C创建并维持列表L1，LD，LSK，LPK，LS分别用于跟踪AI对预言机H1、部分私钥、秘密值、公钥和签名查询。开始时每个列表均为空，假设以下AI的询问都是不同的。

H1查询:列表L1每一项格式为(ID，R，X，h1)，假设AI最多能做q1次H1查询，C在[1，q1]中随机选取一个值K。当C收到AI对H1(IDi，Ri，Xi)查询时，C随机选择h1∈Zq*，返回h1给AI，并将H1(IDi，Ri，Xi，h1)添加到列表L1中。

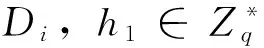
秘密值查询:列表LSK中每一项格式为(ID，X，x)，当C收到对(IDi，Xi，xi)时，若(IDi，Xi，xi)在列表LSK中存在则返回相应的xi给AI；否则，随机选择xi∈Zq*，返回给AI，计算Xi=xiP并将(IDi，Xi，xi)添加到列表LSK中。

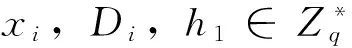
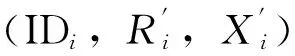
签名查询:当C收到关于身份IDi，公钥为(Ri，Xi)对消息m的签名查询时，C随机选择σ，γ，计算，设置H1(IDi，Q，Xi)=γ，返回(σ，γ)给AI。

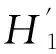
定理2(无证书签名方案在AII攻击下存在不可伪造性):在随机预言模型(ROM)中，若群G上的离散对数问题(DL)是困难的，那么上述的无证书签名方案在敌手AII的攻击下是安全的。

证明:假设C想解决G上的DL问题，其DL问题的输入为(dP，P)，其目标是计算出d。假设AII能以不可忽略的优势攻破我们的签名方案，下面利用AII来解决群G上的DL问题。首先，C生成系统参数params={p，q，P，P0，H1，H2}并将其发给AII。C创建并维持列表L1，LD，LSK，LPK，LS分别用于跟踪AII对预言机H1、部分私钥、私钥、公钥和签名查询。开始时，每个列表均为空，并假设以下AII的查询都是不同的。

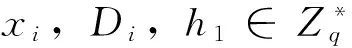
H1查询:列表L1每一项格式为(ID，R，X，h1)，当C收到AII对H1(IDi，Ri，Xi)查询时，C随机选择h1∈Zq*，返回h1给AII，并将H1(IDi，Ri，Xi，h1)添加到列表L1中。

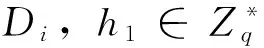
秘密值查询:列表LSK中每一项格式为(ID，X，x)，当C收到AII关于身份为IDi用户的秘密值查询(IDi，Xi，xi)时，若IDi=IDK，则C终止；否则，若(IDi，Xi，xi)在列表LSK中存在则返回相应的xi给AII，若xi=，则表示关于身份IDi对应的公钥经被替换；若(IDi，Xi，xi)不在列表LSK中，则随机选择xi∈Zq*，返回给AII，计算Xi=xiP并将(IDi，Xi，xi)添加到列表LSK中。

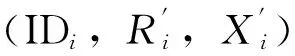
3.2效率分析

将本文提出的签名方案的效率与文献[11]所提的无证书签名方案进行比较如表1所示，其中H表示一个哈希运算，S表示椭圆曲线点群G上的标量乘法，Z1表示Zq*中证书的长度。

表1　计算量和签名长度比较

在签名阶段，计算TA=P需要一次标量乘法，计算h时需要一次哈希运算[11]。在验证阶段，计算h1y需要一次标量乘法，计算hP需要一次标量乘法，计算s1(RA+XA+h1y+hP)和s2(RA+XA+h1y+hP)各需至少一次标量乘法，因此，验证阶段共计计算量4S+1H。本文所提方案，在签名阶段，计算Ti=αP需要一次标量乘法，计算h时需要一次哈希运算。验证阶段，计算u1P需要一次标量乘法，计算h1P0需要一次标量乘法，计算u2(Ri+Xi+h1P0)需要一次标量乘法；计算h1需要一次哈希运算，因此，验证阶段共计计算量3S+1H。验证阶段的效率提高了20。在签名长度方面，本文提出的方案签名长度比文献[11]的签名长度减少了33.3.

4　结束语

论文基于ElGamal签名体制的思想，提出一种新的无需配对的无证书签名方案，并用随机预言模型证明了签名方案的安全性。方案解决了文献[11]中利用方案缺陷使得用户可以在获得一个部分私钥的情况下，恶意生成多个公私钥对的问题，同时，在效率方面也有所提高。

[1]BONEH D，FRANKLIN M K，Identity-based encryption from the weil pairing[C]//Advances in Cryptology-CRYPTO2001.USA:[s.n.]，2001：213-229.

[2]Al-RIYAMI S S，PATERSON K.Certificateless public key cryptography[J].Springer-Verlag，2003：452-473.

[3]CHEN L，CHENG Z，SMART N P.Identity-based key agreement protocols from Pairings[J].Int J Inf Secur，2007，6(4):213-241.

[4]BAEK J，SAFAVI-NAINI R，SUSILO W.Certificateless public key encryption without pairing[M].Heidelberg:Springer，2005，3650:13-148.

[5]DUAN S.Certificateless undeniable signature scheme[J].Information Sciences，2008，178(3):742-755.

[6]ZANG L，ZANG F，QIN B，et al.Provably-secure electronic cash based on certificateless partially-blind signatures[J].Electron Comm Res，2011，10(5):545-552.

[7]JIN Z，WEN Q.Certificateless multi-proxy signature[J].Compute Commun，2011，34(3):344- 352.

[8]ZHANG Z，WONG D，XU J，et al.Certificateless public-key signature:security model and efficient construction[C]//Springer-Verlag.2006：293-308.

[9]CHOI K Y，PARK J H，HWANG J，et al.Efficient certificateless signature schemes[C].Springer-Verlag，2007:443-458.

[10]ZHANG LEI,ZHANG Futai.A method to construct a class of cerificateless signature schemes[J].Chinese Journal of Computers,2009，32(5)：940-945.

[11]WANG Shengbao,LIU Wenhao.Certificateless signature scheme without bilinear pairings[J].Journal on Communications,2012，33(4):93-98.

[12]POINTCHEVAL D,STERN J.Security arguments for digital signatures and blind signatures[J].Journal of Cryptology,2000,12(3):361-369.

Certificateless Signature Scheme without Paring Based on ElGamal Scheme

PENG Cheng1，YANG Dengqi2

(1.School of Mathematics and Statistics，Yunnan University，Kunming 650091，China;2.School of Mathematics and Computer，Dali University，Dali 671003，China)

ElGamal; certificateless signature; without paring

2014-12-22；修改日期: 2015-01-30

国家自然科学基金(11464049)。

彭程(1980-)，男，硕士，实验师，主要从事网络安全、并行算法方面的研究。

TN918.1；G642.0

A

10.3969/j.issn.1672-4550.2016.01.019