山区河流二维推移质数学模型及应用研究——以望谟河整治工程为例

周　维,郜会彩,吴　腾

(1.贵州省水利水电勘测设计研究院 夹岩设计处，贵阳　550002 ；2.绍兴文理学院 土木工程学院, 浙江 绍兴　310020；3.河海大学 港口海岸与近海工程学院，南京　210098)



山区河流二维推移质数学模型及应用研究
——以望谟河整治工程为例

周维1,郜会彩2,吴腾3

(1.贵州省水利水电勘测设计研究院 夹岩设计处，贵阳550002 ；2.绍兴文理学院 土木工程学院, 浙江 绍兴310020；3.河海大学 港口海岸与近海工程学院，南京210098)

为了充分利用我国西南山区丰富的水能资源，同时减少望谟河因山洪引起的高含沙水流洪涝和泥石流灾害，应用二维水流泥沙数学模型常用的控制方程式，采用有限体积法对方程进行离散，并使用“冻结法”对模型中陆地边界进行处理，建立了具有一定通用性的山区河流的二维推移质数学模型。利用建立的模型对贵州省望谟河新屯段进行了流场和推移质冲淤模拟计算，并进行了望谟河整治工程影响分析。结果表明：对于望谟河水位和河床冲淤变形验算，数值模型计算值与经验公式推算变化趋势一致，数值也较为接近；整治工程实施后望谟河沿程的水位绝大部分发生不同程度的降低，仅局部存在微小的抬高；望谟河整治后，同流量下，水位降低，流速归槽泥沙淤积减小，有利于河道防洪。

山区河流；二维推移质；数学模型；冲淤变化;河道整治工程

1　研究背景

推移质输移是河流动力学研究的一个关键问题，也是研究推移质运动和河床冲淤规律的理论基础，同时又是解决河床演变计算、物理模型试验以及数学模拟计算等问题不可缺少的工具。国内外许多学者对推移质进行了研究，据统计，目前各种推移质输沙率公式已超过50个。梅叶-彼得公式是以拖曳力为主要参数的典型公式[1-2]，该公式吸收了大量的试验资料；R.A.Bagnold[3]、张瑞瑾等[4]、张红武等[5]从能量平衡的观点出发，根据推移质输沙特性所得公式，适用于小至细沙,大至卵石的低、高输沙强度的推移质输沙率计算；以冈卡洛夫为代表的前苏联学者建立的一系列公式[6]和我国成都勘测设计院的推移质输沙率公式[7]，以流速为主要参数，此类公式中输沙率与流速4次方成比例，对流速变化十分敏感。过去几十年来，国内外许多学者对已有的输沙率公式进行了验证和比较，但关于推移质输沙率公式的比较尚无定论。一方面，对推移质运动过程的认识并不清晰；另一方面，局限于当前推移质的测量手段，尚无较为准确的推移质实测资料，导致推移质输沙率公式中的参数并不适用于天然河道，因此，给实际应用带来了巨大的困难。

望谟河位于贵州省望谟县境内，历来洪涝灾害频繁。2011年望谟县 “6·06”特大洪水过后，河道及两岸淤积十分严重，河道部分区域淤积厚度达2～3 m，降低了河道的过洪能力；洪水期水位抬高，水流漫出河道，导致两岸农田及建筑物损失严重。为保障人民生命财产安全和地方经济稳定发展，近年实施了望谟河河道治理工程。整治工程修建后在一定程度上改变河道原有的水沙运动及河床变形过程。由于望谟河为山区河流，河床以沙卵石为主，为推移质造床，因此，有必要加深对推移质输移及河道演变规律的理解和认识，为防灾减灾决策制定提供可靠支撑。

本文根据山区河流的特点，建立了具有一定通用性的山区河流二维推移质数学模型，利用建立的模型对贵州省望谟河新屯段进行了流场和推移质冲淤模拟计算。

2　模型的建立

2.1控制方程

二维水流泥沙数学模型可用于描述水沙各运动要素沿水深的平均值、河床高程随流程沿河宽2个方向的变化情况，基于控制体概念并遵循质量守恒定律和牛顿第二定律，可导出二维水流泥沙数学模型经常采用的控制方程式，即

(1)水流连续方程：

(1)

式中：Z为水位；t为时刻；h为水深，h=Z-Zb，Zb为河底高程；u，v分别为垂线平均流速沿x，y方向的分量。

(2)水流运动方程：

(2)

(3)

式中：f为柯氏力；g为重力加速度；νt表示紊动黏性系数；n为糙率系数。

(3)悬移质不平衡输沙基本方程：

(4)

(4)推移质不平衡输沙基本方程：

本次计算采用窦国仁导出的推移质不平衡输沙方程，即

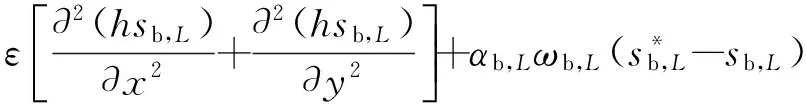
(5)

(5)河床变形方程(不平衡输沙法)：

(6)

2.2方程的离散

本模型采用有限体积法对方程进行离散，其基本思想是：将计算区域划分为若干规则或不规则相互连接但不相互重叠的单元，将变量定义在控制体形心，对基本方程在每个控制体内积分。得出一组以计算节点上物理量为未知数的代数方程组来求解。

2.3边界处理

陆地边界的处理方法是：令闭边界的法向流速为0，而沿切线方向的流速为非0值。随着水位的变化，陆地边界位置不断变化。本模型采用“冻结法”处理这种问题，根据计算水位和湖底高程判断网格单元是否露出水面，即定义临界水深h=0.005～0.01 m，当水深h>h时，糙率取正常值，反之糙率取一大值(1010量级)。

3　模型的验证

3.1典型条件下数学模型的验证

实际工程中溃坝大部分出现局部、部分的溃决。部分溃坝有着间断流，急流，非恒定流等特性，是非常经典的例子。本文研究的模型尺寸如图1所示，坝的中间有75 m的溃决口，初始水位为10 m。图2为部分溃坝后7 s时的水面图。由图2可以看出，上游两侧水流均向中间流动，在水面中间处形成低谷。随着波不断向上传播，低谷也不断往上游移动。此外，在溃口两侧拐点处产生明显回流。

图1　溃坝模型尺寸Fig.1　Size of dam-break model

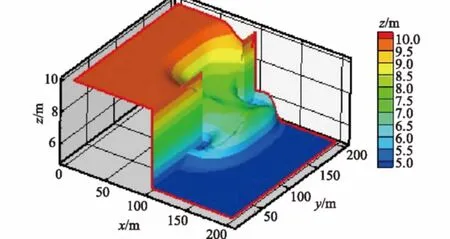
图2　溃坝后t=7 s水面Fig.2　Water surface at 7 s after dam break

为了进一步验证算法，把本文计算结果与S.Fagherazzi等[8]计算的结果进行比较，如图3所示。总体而言，两者计算值较为接近，可以模拟溃坝的流态。

图3　水面等势线计算结果对比Fig.3　Comparison of calculated results of water surface contours

3.2望谟河的验证

3.2.1水位验证

本次计算选取的范围为望谟河新屯至东岩段设计防洪治理河道长度为1.647 km的整治河段，网格数为289×95，网格长度为7 m，计算过程中时间步长取10 s。由于望谟河整治河段内无沿程的实测水位、流速等数据，因此，本次验证采用经验公式推算的水位与本模型计算的水位进行类比(该成果已通过专家验收)。图4(a)、图4(b)分别为5%频率洪水验证水位和2011年洪水沿程水位，可以看出，数值模型计算值与经验公式推算值变化趋势一致，数值也较为接近，初步说明本文建立的模型能应用于望谟河的研究。

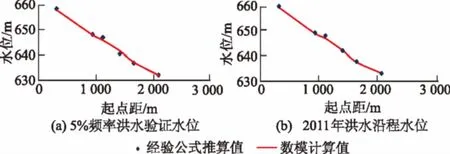
图4　 经验公式和数值模型计算水位值对比Fig.4　Comparison of water levels obtained from empirical formula and simulation

3.2.2河床冲淤变形验证

根据搜集到的实测资料，望谟河2011年洪水过后河道内泥沙淤积厚度为2～3 m，限于实测资料，验证计算模拟该场次洪水后河道的冲淤变化。图5为数值模型计算的2011年洪水后望谟河河道冲淤变化分布，由淤积分布可知，该洪水条件下河段的绝大部分发生淤积，淤积厚度为2～3 m，局部发生冲刷，冲刷范围和幅度均较小。计算结果表明，该模型也可以初步运用于模拟望谟河的河床冲淤变形。

图5　2011年洪水后望谟河河道冲淤变化Fig.5　Scouring and deposition of Wangmo river after the flood period in 2011

4　望谟河整治工程影响分析

4.1数值模型计算条件

为了更好分析望谟河整治后的效果，选取10 a一遇洪水，计算分析整治工程对水位、流速的影响。数值模型计算的条件为：上游来流量400 m3/s，下游水位为631.58 m。图6为数值模型水位测点及测量断面分布图。

图6　工程区测点及测量断面分布Fig.6　Layout of observation points and observation sections

4.2望谟河整治对水位的影响

表1为望谟河整治河段工程实施前后测点水位变化。由表1可知，10 a一遇洪水条件下，整治工程后沿程绝大部分河段的水位发生不同程度降低，仅在D2断面和D3断面水位存在微小的抬高，分别抬高0.06 m和0.01 m。具体而言，进口断面至D3断面水位差有逐渐减小趋势，从D3断面至D5断面水位差有逐渐增大趋势，D1断面的最大水位差为0.72 m，D2断面最大水位差0.21 m，同时该断面部分测点水位差出现负值，D3断面整治前后水位变化不大，D4断面及其下游水位差增大迅速，水位差最大值出现在D4-1断面，为2.44 m。该计算结果表明，望谟河整治后，由于河槽变深，同水位下过水面积增大，水位降低，望谟河整治有利于河道防洪。

4.3望谟河整治对流态的影响

图7为10 a一遇洪水条件下整治前后流速比较。由图7可以看出，D1断面上游，河道未进行疏浚，整治前后流速和流向变化不大，但整治后有向主河槽集中的趋势；D1至D1-2河段，主河槽流速增大，滩地流速减小；D1-2至D1-3河段，整治后流速较整治前流速减小，主要由于河道疏浚后，河槽过水面积增大导致流速降低，但水流均有归槽趋势；D1-3至D3-1河道内，滩面流速归槽明显，尤其是在D2河段附近，未疏浚时有明显水流，但河道疏浚后，水流均在河槽中运动，水流未漫滩，有利于汛期的防洪；D3-1至D5-1河道内流速变化不大，流向偏向疏浚的河槽；D5-1断面下游，水流流向变化不明显，流速稍有减小。工程区域内，整治前最大流速出现在D2断面，流速大小为4.33 m/s，整治后最大流速出现在D5断面，最大流速为4.08 m/s；整治后与整治前流速差异最大值出现在D2断面，流速差为2.86 m/s，主要由于主流归槽的影响。

表1　整治前、后测点水位变化

注：水位差为整治前水位减整治后水位，“—”为不过水。

注：实心箭头为整治前，空心箭头为整治后图7　10 a一遇洪水条件下整治前、后流速比较Fig.7　Comparison of flood velocity before and after river project under flood probability of 10%

4.4望谟河整治后洪水条件下河道演变分析

根据望谟河的实测洪水资料分析，本次计算模拟洪水的历时为5 h，河床的中值粒径为5 cm。图8为修建工程后遇2011年洪水河道的冲淤分布。

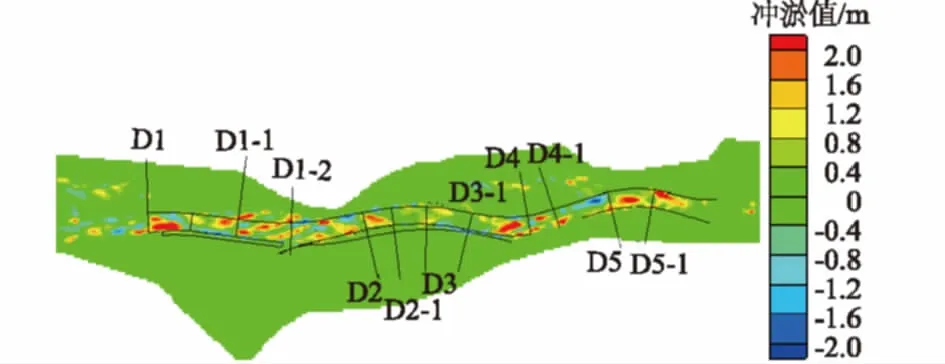
图8　河道整治后遇2011年洪水河道冲淤分布Fig.8　Scouring and deposition of Wangmo river encountered with flood in 2011 after river regulation

由图8可知，该条件下望谟河道主要以淤积为主，局部区域存在冲刷。淤积厚度的变化规律为：洪水频率越大，望谟河泥沙淤积的厚度也越大，尤其是D1断面至D2断面间以及D4断面至D5-1断面间河道淤积较大。该变化规律的主要原因是该河段的淤积主要由于上游来的推移质泥沙，当洪水越大时上游的来沙量越大，当流速稍有减小则可能发生淤积，故在该区域的淤积也会越大。此外，根据计算结果也表明，当发生5 a一遇洪水时，该计算区域的泥沙淤积量并不大，仅在河道的D1断面、D4断面和D5-1断面产生较大的淤积，其余区域则淤积较小。河道整治后，河道淤积量较整治前(图5)明显减小。

5　结　语

基于山区河流的水沙运动特性，建立了适用于望谟河水沙数学模型，并采用该模型对望谟河整治工程的效果进行了计算分析。计算结果表明：

(1)整治工程实施后望谟河沿程的水位绝大部分发生不同程度的降低，仅在D2断面至D3断面水位存在微小的抬高。水位差的变化规律为：D1断面至D3断面水位差有逐渐减小趋势，从D3-1断面至D5-1断面水位差有逐渐增大趋势。水位差最大值均出现在D4-1断面，10 a一遇洪水条件下整治后水位降低最大为2.44 m。

(2)10 a一遇洪水条件下，D1断面上游，整治前后流速大小差异不大；D1至D1-3河段，整治后流速较整治前流速稍小；D1-3至D3-1河道内，滩面流速归槽明显，尤其是在D2河段附近，整治前右侧过流，整治后右侧不过流，该条件下整治后洪水的淹没范围较整治前减小较大；D3-1至D5-1河段内流速变化不大，水流流向疏浚的河槽；D5-1断面下游，水流流向变化不明显，流速稍有减小，同时滩地上的过流量减小。

(3)望谟河整治后，同流量下，水位降低、水流归槽泥沙淤积减小，有利于河道防洪。

[1]MEYER-PETER E ,MULLER R.Formulas for Bed Load Transport[C]∥International Association of Hydraulic Research .Proceedings of 2nd Meeting of the International Association for Hydraulic Structures Research.Delft,Netherlands,June 7,1948:39-64.

[2]MEYER-PETER E,FAVRE H,EINSTEIN H A.Neuere Versuchsresutate Uber den Geschiebetrieb[J].Schweizerische.Bauzeitung,1934,103(12):147-150.

[3]BAGNOLD R A.An Approach to the Sediment Transport Problem from General Physics[R].Washington,USA:United States Government Printing Office ,1996.

[4]张瑞瑾，谢鉴衡．河流泥沙动力学[M]．北京：水利电力出版社，1998.

[5]张红武,张俊华,卜海磊,等.试论推移质输沙率公式[J].南水北调与水利科技,2011，9(6)：140-145.

[6]谢鉴衡．河流泥沙工程学(上册)[M]．北京：水利电力出版社,1982.

[7]李昌华，金德春．河工模型试验[M]．北京：人民交通出版社，1981.

[8]FAGHERAZZI S,RASETARINERA P,HUSSAINI M Y,et al.Numerical Solution of the Dam-Break Problem with a Discontinuous Galerkin Method[J].Journal of Hydraulic Engineering,2004,130(6):532-539.

(编辑：占学军)

Application of 2-D Numerical Model of Bed Load in Riversof Mountain Area：Regulation Project in Wangmo River as An Example

ZHOU Wei1,GAO Hui-cai2,WU Teng3

(1.Design Department of Jiayan Project ,Guizhou Investigation and Design Institute of Water Conservancy and Hydropower,Guiyang550002,China; 2.College of Civil Engineering,Shaoxing University,Shaoxing 310020,China; 3.College of Harbour,Coastal and Offshore Engineering,Hohai University, Nanjing210098,China)

In order to utilize rich hydropower resources in southwest mountain area of China and decrease flow with high sand proportion and debris flow disasters caused by flash flood,we should establish suitable two-dimensional bed load mathematical models for rivers in mountain area.On the basis of finite volumetric method,we dispersed common controlling equations in sediment numerical model of two-dimensional flow,dealt with dry land boundary by using frozen method,and established a general two-dimensional bed load mathematical model.Xintun section in Wangmo river located in Guizhou province was taken as an example.We carried out numerical calculation of flow field,exploring scouring and deposition of bed load.Test results showed that,as for water level calculation and verification of scouring and deposition in the river bed,simulated data was in consistent with data from empirical formula; after regulation project of the river,most of water levels along the flow direction decreased,except for slight increase in few sections; meanwhile,in the condition of given discharge，water level after the regulation was smaller than that before the regulation,and sediment deposition into the water flume decreased,which is in favor of river flood control.

river in mountain area; two-dimensional bed load; numerical model; scouring and deposition; river regulation project

2015-06-04;

2015-08-19

国家自然科学基金项目(51309084);贵州省水利科技项目(KT201303);浙江省公益技术应用研究计划项目(2015C31134)

周维(1982-)，男，贵州仁怀人，高级工程师，主要从事水工建筑物设计和河流泥沙研究，(电话)0851-85584296(电子信箱)287043164@qq.com。

郜会彩(1979-)，女，河南鄢陵人，高级工程师，硕士，主要从事河流泥沙和泥石流研究，(电话)15215998120(电子信箱)gaohuicai@sina.com。

10.11988/ckyyb.201504732016,33(08):6-10

TV92

A

1001-5485(2016)08-0006-05