考虑非线性环境量影响的混凝土重力坝坝基扬压力分析

徐　蔚，方春晖，王　雪,朱　凯

(1.浙江水利水电学院 建筑工程学院，杭州　310018；2.浙江省水利河口研究院，杭州　310020；3.浙江同济科技职业学院 水利工程系，杭州　311231; 4.河海大学 水文水资源与水利工程科学国家重点实验室，南京　210098)



考虑非线性环境量影响的混凝土重力坝坝基扬压力分析

徐蔚1，方春晖2，王雪3,朱凯4

(1.浙江水利水电学院 建筑工程学院，杭州310018；2.浙江省水利河口研究院，杭州310020；3.浙江同济科技职业学院 水利工程系，杭州311231; 4.河海大学 水文水资源与水利工程科学国家重点实验室，南京210098)

基于混凝土重力坝上游库水位及降雨对其坝基扬压力影响的滞后效应及其非线性特征，建立了考虑环境量非线性影响过程的混凝土重力坝坝基扬压力监测模型，将上游库水位及降雨对坝基扬压力的影响视为一个正态分布过程，并采用量子遗传算法，对相应滞后天数和影响天数进行智能寻优，以提高拟合及预测精度。最后，以某混凝土重力坝为例，采用上述方法对其A6-UP-01测点扬压力测值进行拟合和预测，通过与坝基扬压力实测值对比分析，验证了本文方法优于传统坝基扬压力统计模型，具有一定科学和实践应用价值。

混凝土重力坝；扬压力；滞后效应；传统统计模型；分组量子遗传算法

1　研究背景

混凝土重力坝渗流安全性评价是大坝安全监控的重要组成部分，其中坝基扬压力作为作用在混凝土重力坝上的主要荷载，其大小直接影响坝体的稳定性[1]。研究表明，坝高100 m左右的重力坝，坝基面上作用的扬压力大约是坝体重量的20%[2]。而大坝监测资料分析表明，坝身混凝土及基岩在上游库水压力的作用下，其防渗性能具有逐渐降低的趋势[3-5]。因此，及时整理分析坝体、坝基扬压力的观测资料，建立坝基扬压力统计模型并分析相应的变化规律，对于验算大坝的稳定性和耐久性，掌握大坝的安全性态，了解坝身混凝土的抗渗性能以及坝基的帷幕、排水效应和坝基情况的变化等，都具有十分重要的意义[6-7]。

传统混凝土坝坝基扬压力统计模型中将前期库水位或降雨对测压管水位的影响视为一个“平均”的过程[1]，即取观测日前i天的库水位平均值对测压管水位进行拟合，而实际上，上游水位对混凝土重力坝坝基扬压力的影响是一个先增长后下降的过程，而不是一个平均的过程，为此需要深入研究其因子的选择。

因此，本文结合混凝土重力坝渗流机理，综合考虑上游库水位及降雨对坝基扬压力的非线性影响，将前期库水位及降雨对测压管水位的影响视为一个正态分布过程，建立混凝土重力坝坝基扬压力统计模型，并以某混凝土重力坝为例，采用改进遗传算法对上游库水位分量及降雨分量的滞后天数与影响天数进行智能寻优，确立最终混凝土重力坝坝基扬压力统计模型。最后，通过将本文方法拟合结果与混凝土重力坝坝基扬压力传统统计模型拟合结果进行对比分析，验证了本文方法有效性。

2　基本理论

2.1混凝土重力坝坝基扬压力统计模型

根据实测资料分析表明，混凝土重力坝坝基扬压力主要受上游水位、降雨、基岩温度及坝前淤积、坝基帷幕防渗和排水效应的时变特性等影响[1-2]。为此，本文混凝土重力坝坝基扬压力统计模型采用的形式为

(1)

式中：P为坝体测压管水位;PH是水位分量;PR是降雨分量;Pθ是时效分量;PT为温度分量。

2.1.1水位分量PH

通过综合考虑混凝土重力坝坝体坝基扬压力与上游库水位非线性关系，不同于传统统计模型将上游水位对坝基扬压力的影响视为一个“平均”的过程，如图1。根据上游水位对坝基扬压力的影响过程，如图2，其基本服从正态分布过程，称为影响曲线。

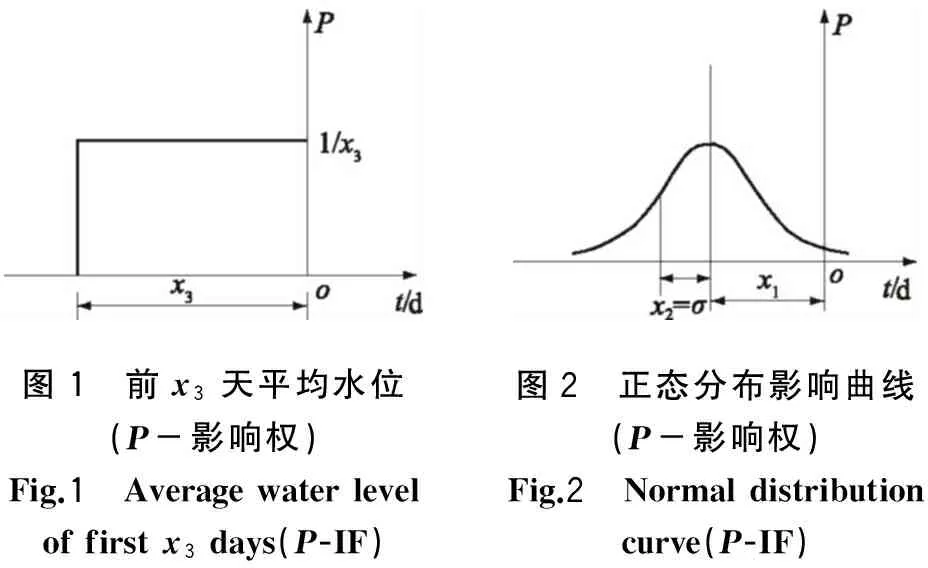
图1 前x3天平均水位(P-影响权)Fig.1 Averagewaterleveloffirstx3days(P-IF)图2 正态分布影响曲线(P-影响权)Fig.2 Normaldistributioncurve(P-IF)

基于此，相应混凝土重力坝坝基扬压力上游水位分量采用形式为

(2)

式中：aj为水位分量的回归系数；x1为水位分量的滞后天数；x2为水位分量的影响天数；Hi(t)为上游水位；Hef为有效水位。

其中，x1，x2需要通过试算求得，在求得实际滞后天数和影响天数后，即可提高坝基扬压力统计模型回归精度，为评价防渗效果提供依据。此外，上游水位一般每天只要一个测值。因此，本文将连续性积分改成离散型积分，积分区间只需取x2的2～3倍即可满足要求。

2.1.2降雨分量PR

在降雨过程中，有一部分入渗产生地下水，地下水主要通过节理裂隙渗流影响两岸坝段坝基的扬压力[8]。在该过程中呈明显的非线性关系，并且具有滞后效应，采用前期降雨量的均值作为因子，同样存在难以精确模拟降雨对扬压力的影响。

单元裂隙岩体中渗流基本服从指数定律，即

(3)

式中：v为渗流速度；k为渗透系数；u为孔隙水压力；γw为水的重度；m为指数形式渗流定律的指数，m∈[0.5,3.25]。

根据降雨对地下水位的影响规律和裂隙渗流的指数定律，本文坝基扬压力降雨分量采用形式为

(4)

式中：bi为降雨分量的回归系数；x3为降雨分量的滞后天数；x4为降雨影响权正态分布标准差(影响天数)；R(t)为t时刻的单位时段降雨量；Ref为有效降雨量。

同样x3和x4经过试算求得，连续性积分可转化为离散型积分。

2.1.3温度分量PT

渗流受地基裂隙变化的影响，孔隙变化受基岩温度的作用[9-11]。而基岩温度变化较小，基本呈年周期变化规律，本文采用正弦波周期函数作为温度分量,即

(5)

式中c1i,c2i为温度分量的回归系数。

2.1.4时效分量Pθ

时效分量是混凝土重力坝坝基扬压力的重要组成部分，也是评价大坝渗流稳定性的重要依据，本文将坝体测压管水位时效分量表示为

(6)

式中：d1,d2分别为时效分量线性项、对数项的回归系数；θ为从蓄水初期或工程措施初期开始的天数除以100，即每100 d增加1.0。

综上，本文所取混凝土重力坝坝基扬压力统计模型为

(7)

然而，采用常规方法计算库水位和降雨对坝基扬压力影响的滞后天数及影响天数效率低、精度差，为此本文采用改进遗传算法对上述参数进行智能寻优，提高计算效率和精度。

2.2分组量子遗传算法

量子遗传算法(quantum genetic algorithm，QGA)结合量子计算与遗传算法，是一种新发展起来的概率进化算法[12-13]。该方法以量子理论为基础，采用量子位概率编码表示染色体，通过不断更新量子旋转门的作用来更新和优化种群，达到搜索的目的。其具有种群规模小，收敛迅速和全局寻优能力强等特点，并在求解组合优化问题中取得显著成效[14-15]。

1个量子位可以处于0态、1态、以及|0〉和|1〉之间的任意叠加态。可以表示为

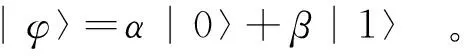
(8)

(9)

因此，

(10)

(11)

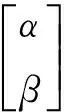
(12)

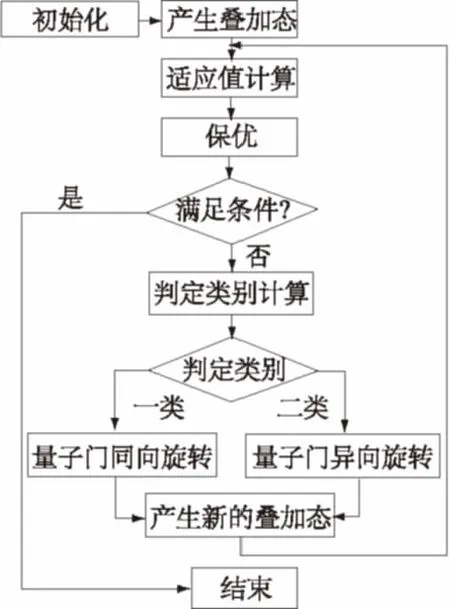
图3　算法流程Fig.3　Flow chart of algorithm

在分组量子遗传算法中，量子旋转门可以表示为[16]

(13)

量子门更新过程可以表示为

(14)

(15)

所以，可以得出：

(αisinθi+βicosθi)2=

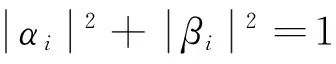
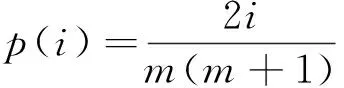
3　工程实例

3.1工程简介

某水电站位于云南省丽江市境内，电站设计总装机容量为240万kW，坝顶全长640 m，最大坝高160 m，总库容9.13亿m3。枢纽工程由碾压混凝土重力坝、右岸溢洪道、左右岸坝身泄洪冲沙孔和坝后厂房等建筑物组成，右岸台地布置5孔开敞式溢洪道，其最大泄洪流量为14 980 m3/s，坝后厂房安装4台单机容量600 MW水能发电机组。水库正常蓄水位1 418 m，校核水位1 421.07 m，相应库容8.47亿m3，具有周调节能力，控制流域面积237 357.6 km2。电站运行时保证出力473.7 MW，年平均发电量110.43亿kW·h，发电效益显著，是“西电东送”战略目标的骨干电站之一。

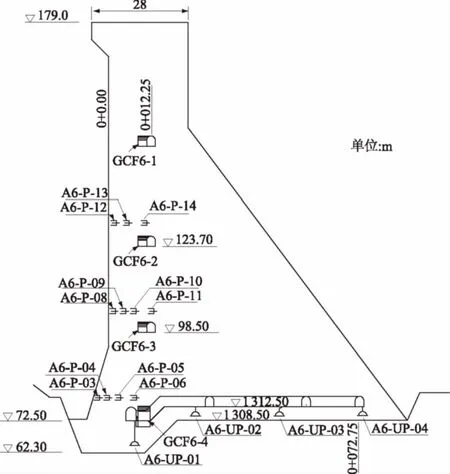
图4　大坝渗流监测布置Fig.4　Layout of monitoring points for dam seepage

为了监测大坝渗流状况，根据监测施工单位统计，大坝共安装渗压计106支，量水堰9座、坝基测压管46个、水位孔11个、水力学底座131个，其中坝纵0+157.50 m断面大坝渗流监测布置图如图4。

监测资料分析表明，该坝段A6-UP-01测点坝基扬压力监测数据常年处于较高水平，因此本文将对该测点进行重点分析。

3.2混凝土重力坝坝基扬压力分析

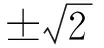
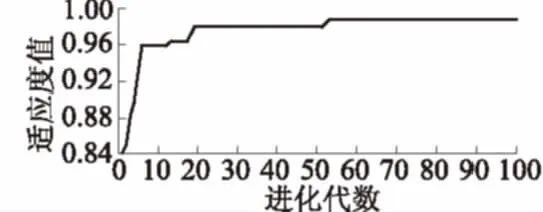
图5　最优个体适应度值演化曲线Fig.5　Evolution curve of optimal individual fitness value

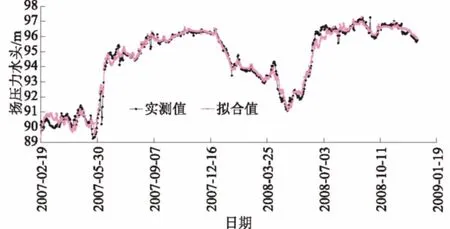
图6　本文方法拟合结果Fig.6　Fitting result of the proposed method

由图5、图6可知，采用分组量子遗传算法最终优化复相关系数为0.981，A6-UP-01测点扬压力实测值与拟合值变化规律相同，本文方法具有较高的拟合精度。此外，可以注意到坝基扬压力实测值在个别日期具有突变现象，初步分析为相应上游库水位及降雨突变所致。

为进一步验证上述方法有效性，本文同时采用传统混凝土坝坝基扬压力统计模型[1]对A6-UP-01测点测值进行拟合，该统计模型为

(16)

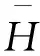
取m1=m2=m3=5，采用逐步回归分析对A6-UP-01测点坝基扬压力测值进行拟合，拟合结果如图7。

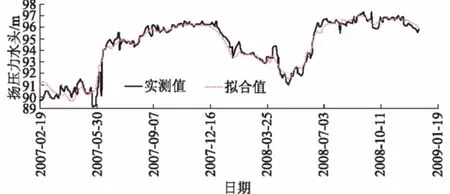
图7　传统方法拟合结果Fig.7　Fitting result of the traditional method

由图7可知，传统坝基扬压力统计模型拟合结果与坝基扬压力实测值偏差较大，最终复相关系数为0.91，与本文方法相比，传统混凝土坝坝基扬压力统计模型拟合效果较差。

传统方法和本文方法拟合残差序列对比如图8，可知本文方法拟合结果明显优于传统统计模型。此外，可以看出传统统计模型拟合残差具有许多突变点，表明该传统模型无法体现出由于上游库水位及降雨引起的坝基扬压力测值突增现象。

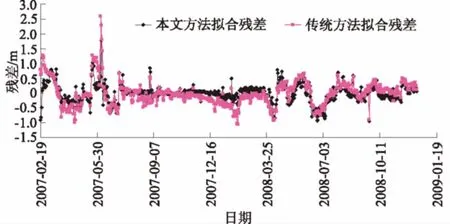
图8　两种方法拟合残差对比Fig.8　Comparison of fitting residual between the two methods

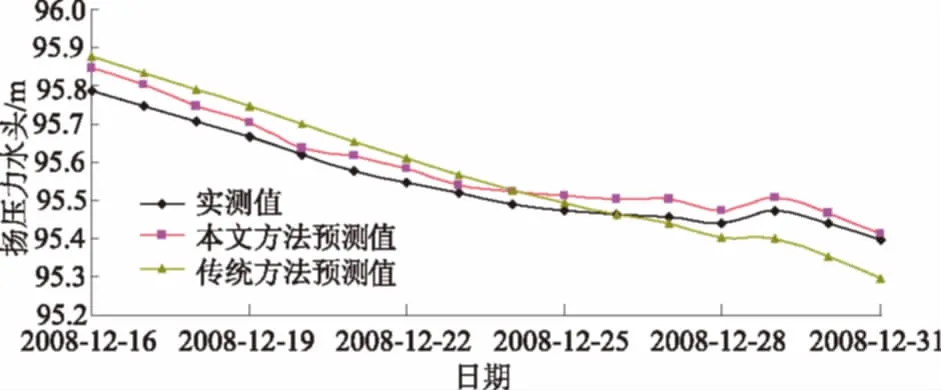
图9　2种方法预测结果对比Fig.9　Comparison of predicted values between the two methods

为了进一步验证本文方法有效性，本文采用上述2组模型对A6-UP-01测点2008年12月16—31日坝基扬压力进行预测，2组模型预测结果及坝基扬压力实测值如图9。

由图9可知，本文方法预测结果相比传统统计模型具有更高的预测精度，此外，由于本文模型考虑了前期库水位及降雨对坝基扬压力测值的非线性影响，因此本文模型能够预测出2008年12月25—31日坝基扬压力测值的非线性变化。

4　结　论

本文基于前期库水位及降雨对混凝土坝坝基扬压力的非线性影响特性，将上游库水位及降雨对混凝土坝坝基扬压力的影响视为“正态”分布过程，并采用改进遗传算法，对相应滞后天数和影响天数进行智能寻优，以提高拟合精度，通过与传统统计模型拟合结果对比分析，可以得出如下结论：

(1)通过将上游库水位及降雨对坝基扬压力的影响过程视为一个“正态”分布过程，本文方法相比传统方法拟合精度更高，并且能够体现出由于上游库水位及降雨引起的坝基扬压力突增现象。

(2)通过考虑上游库水位及降雨对坝基扬压力的非线性影响，本文方法相比传统方法更能够预测出坝基扬压力的非线性变化趋势，而传统统计模型将前期库水位及降雨对坝基扬压力的影响视为一个“平均”过程，则无法体现出该特征。

(3)分组量子遗传算法结合量子运算原理和遗传算法，利用量子的态矢量替代二进制符号来实现遗传编码过程，利用量子逻辑门实现对个体染色体的更新，提高了个体寻优效率，且不依赖初始种群，具有全局收敛特性，避免了传统遗传算法容易产生局部极值的现象。

[1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.

[2]顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.

[3]江建国.大坝混凝土渗透系数反演及其随时间的变化规律[J].黑龙江水专学报，2007,34(2):30-31.

[4]速宝玉，胡云进，刘俊勇，等.江垭碾压混凝土坝芯样渗透系数统计特性研究[J].河海大学学报：自然科学版， 2002,30(2):1-5.

[5]李波，顾冲时，李智录，等.基于偏最小二乘回归和最小二乘支持向量机的大坝渗流监控模型[J].水利学报， 2008,39(12):1390-1394.

[6]骆进军，李波，李立辉.基于神经网络的大坝岩体渗透系数张量反演分析[J].水电能源科学， 2008,26(5):54-56.

[7]洪云，杨诗经，郑东键.古田溪一级大坝的渗流统计分析及其防渗效应研究[J].水电自动化与大坝监测，1994，(6):33-37.

[8]苏怀智，孙小冉.混凝土坝渗流性态综合评价与趋势预估模型研究[J].人民长江， 2013,44(22):95-99.

[9]顾冲时,李波,徐宝松,等.碾压混凝土坝渗漏安全监控模型建模方法研究[J].河海大学学报:自然科学版,2008,36(5):579-584.

[10]谢红，张家发，龙文九.三峡大坝基础渗流控制措施效果分析[J].长江科学院院报,1998,15(1):34-38.

[11]何鲜峰，顾冲时，谷艳昌.分形-混沌混合预测模型在大坝安全监测中的应用[J].武汉大学学报(工学版)， 2008,41(1):45-49.

[12]HAN K,KIM J.Genetic Quantum Algorithm and Its Application to Combinatorial Optimization Problem[C]∥IEEE Neural Network Council.Proceedings of the 2000 Congress on Evolutionary Computation,La Jolla Marriott Hotel ,USA,July 16-19,2000:1354-1360.

[13]SHU Z,WEI P,BIN L,et al.A Novel Quantum Genetic Algorithm Based on Particle Swarm Optimization Method and Its Application[J].Acta Electronica Sinica， 2006,34(5):897-901.

[14]罗红明.量子遗传算法及其在地球物理反演中的应用研究[D].武汉：中国地质大学,2007.

[15]范胜辉.量子进化算法及其应用研究[D].南京：南京航空航天大学,2010.

[16]郭海燕，金炜东，李丽，等.分组量子遗传算法及其应用[J].西南科技大学学报：自然科学版，2004,19(1):18-21.

(编辑：曾小汉)

Uplift Pressure at Dam Base of Concrete Gravity DamConsidering the Nonlinear Environmental Impacts

XU Wei1,FANG Chun-hui2,WANG Xue3,ZHU Kai4

(1.Architectural Engineering Institute,Zhejiang University of Water Resources and Electric Power,Hangzhou 310018,China;2.Zhejiang Institute of Hydraulics & Estuary,Hangzhou310020,China; 3.Department of Hydraulic Engineering,Zhejiang Tongji Vocational College of Science and Technology,Hangzhou 311231,China; 4.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University,Nanjing210098,China)

In view of the lag effect and the nonlinear characteristics of the influence of upstream water level and rainfall on the uplift pressure of concrete gravity dam,a monitoring model of the concrete gravity dam considering

the nonlinear environmental influence is established.The influential process is regarded as a normal distribution process and the lagging days and influential days are optimized by improved quantum genetic algorithm to raise the fitting and forecasting accuracy.Finally,a concrete gravity dam is taken as an example and the corresponding uplift pressure series of the measuring point A6-UP-01 are fitted and predicted with the proposed method.Through comparison between measured data and predicted data,the proposed method is verified superior to the traditional statistic model and it is of scientific and practical application value.

concrete gravity dam; uplift pressure; hysteresis effect; traditional statistical model;classified quantum genetic algorithm

2015-06-06；

2015-06-18

徐蔚(1972-)，女，浙江杭州人，副教授，硕士，主要从事土木工程防灾减灾研究，(电话)0571-86929055 (电子信箱)sltrgq@163.com。

10.11988/ckyyb.201504782016,33(08):42-46，58

TV698.1

A

1001-5485(2016)08-0042-05