天体运动的几种模型

李良伟

(江西省石城中学　江西 赣州　342700)



天体运动的几种模型

李良伟

(江西省石城中学江西 赣州342700)

天体运动有4种模型，本文以2015年部分高考试题为例，总结出各种天体运动模型的运动和受力特点，以期举一反三.

天体运动模型运动特点受力特点

天体运动是高考中必考的内容之一，一般以选择题形式出现.天体运动形式多样,公式变化繁杂,题目设计问法多样,数据计算复杂，因而学生普遍感到学习困难.从物体受力与运动关系出发，紧扣万有引力与向心力的关系，便可迅速找到解题方法.天体运动一般有以下几种模型.

1　匀速圆周运动模型

1.1围绕中心天体做匀速圆周运动

行星或卫星围绕中心天体做匀速圆周运动时，其轨道平面一定过中心天体中心，万有引力等于向心力(F引=man)，此时重力与万有引力相等(mg′=F引)，也就有mg′=man.

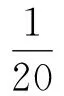
A．1∶10 B．1 C．5D．10

解析：由题意知，“51 peg b”绕其中心恒星做匀速圆周运动，有

化简得

可得恒星质量与太阳质量之比约为1，所以B正确.

1.2双星模型

在远离其他天体的空间中，两颗离得较近的天体围绕它们连线上某点做匀速圆周运动时，两颗星体的角速度一定相等，万有引力等于向心力(F引=man).特别注意两天体之间的距离等于两天体做匀速圆周运动的轨道半径之和.

瓷器的装饰纹饰有两大类：一类继承陶器装饰传统，以图案饰之；一类则是创新，彩绘中国画。无论是继承，还是创新，以表达人类的思想情感为主旨的理念没变。

【例2】神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时，发现了LMCX-3双星系统，它由可见星A和不可见的暗星B构成.两星视为质点，不考虑其他天体的影响，A，B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图1所示.引力常量为G，由观测能够得到可见星A的速率v和运行周期T.恒星演化到末期，如果其质量大于太阳质量ms的2倍，它将有可能成为黑洞.若可见星A的速率v=2.7×105m/s，运行周期T=4.7π×104s，质量m1=6ms，试通过估算来判断暗星B有可能是黑洞吗？(G=6.67×10-11N·m2/kg2，ms=2.0×1030kg)

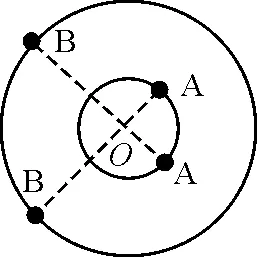
图1

解析：由题意知，A，B两星构成“双星”模型，设A，B的圆轨道半径和质量分别为r1，r2和m1，m2，A，B两星间距为r=r1+r2，对可见星A有

又因为

m1ω2r1=m2ω2r2

得

r1∶r2=m2∶m1

以上关系式可得

设m2=nms，(n>0)，将其和m1=6ms及相关数据代入上式，得

(1)

(2)

由式(2)可知，若使式(1)成立，则n必须大于2，即暗星B的质量m2必须大于2ms，由此得出结论：暗星B有可能是黑洞．

1.3三星模型

在远离其他天体的空间存在3颗星体，它们以受到的万有引力的合力为向心力做匀速圆周运动，三星的角速度也一定相等.

【例3】(2015年高考安徽卷第24题)由3颗星体构成的系统，忽略其他星体对它们的作用，存在着一种运动形式:3颗星体在相互之间的万有引力作用下，分别位于等边三角形的3个顶点上，绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图2所示为A，B，C三颗星体质量不相同时的一般情况).若A星体质量为2m，B和C两星体的质量均为m，三角形边长为a.求：

(1)A星体所受合力大小FA；

(2)B星体所受合力大小FB；

(3)C星体的轨道半径RC；

(4)三星体做圆周运动的周期T.

图2

解析：(1)由万有引力定律，A星体所受B，C星体引力大小为

方向如图3，则合力大小为

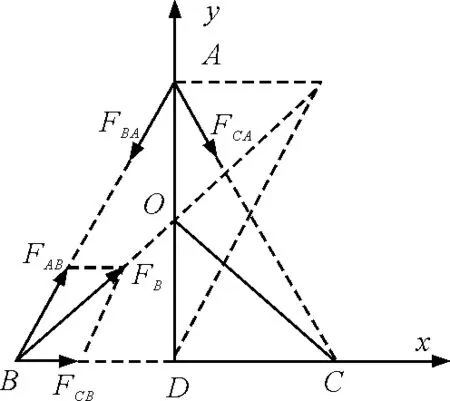
图3

(2)同上，B星体所受A,C星体引力大小分别为

方向如图3，则合力大小为

可得

(3)通过分析可知，圆心O在中垂线AD的中点

(4)三星体运动周期相同，对C星体由

可得

1.4地面模型

如图4所示，放在地面的物体A随着地球一起做匀速圆周运动，轨道平面为某一纬度平面，万有引力沿轨道平面指向地轴的分力等于向心力Fn，另一分力则为重力mg.由于地球的自转速度较小，向心力大约只有万有引力的0.34%，故可认为mg=F.在其他星球表面情况类似.

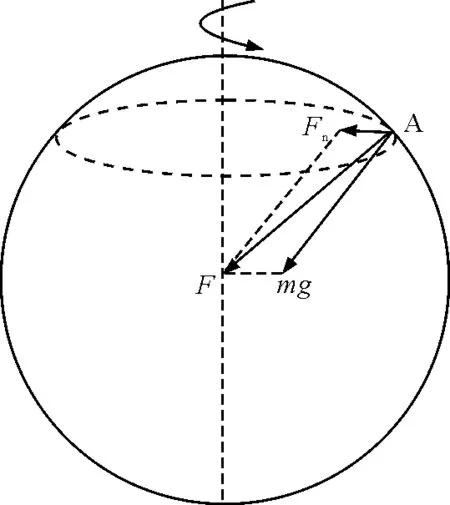
图4

【例4】(2015年高考新课标Ⅰ卷第21题)我国发射的“嫦娥三号”登月探测器靠近月球后，先在月球表面附近的近似圆轨道上绕月运行；然后经过一系列过程，在离月面4 m高处做一次悬停(可认为是相对于月球静止)；最后关闭发动机，探测器自由下落，已知探测器的质量约为1.3×103kg，地球质量约为月球质量的81倍，地球半径约为月球半径的3.7倍，地球表面的重力加速度约为9.8 m/s2,则此探测器

A. 着落前的瞬间，速度大小约为8.9 m/s

B. 悬停时受到的反冲作用力约为2×103N

C. 从离开近月圆轨道这段时间内，机械能守恒

D. 在近月圆轨道上运行的线速度小于人造卫星在近地圆轨道上运行的线速度

解析:在中心天体表面上万有引力提供重力

则可得月球表面的重力加速度

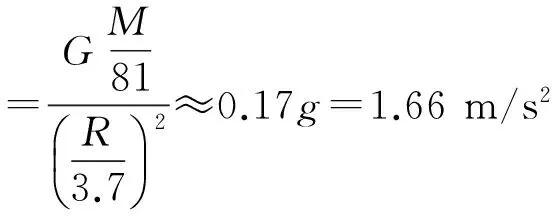
根据平衡条件，探测器悬停时受到的反作用力F=G探=m探g月≈ 2×103N，选项B正确；探测器自由下落，由v2=2g月h,得出着落前瞬间的速度v≈3.6 m/s ,选项A错误；从离开近月圆轨道，关闭发动机后，仅在月球引力作用下机械能守恒，而离开近月轨道后还有制动悬停，发动机做了功，机械能不守恒，故选项C错误；在近月圆轨道万有引力提供向心力

解得运行的线速度

小于近地卫星线速度，选项D正确.

2　椭圆轨道模型

行星或卫星围绕中心天体运动的轨道是椭圆时，万有引力不等于向心力，在近地点，万有引力小于向心力，做离心运动；在远地点，万有引力大于向心力，做向心运动.

图5

【例5】如图5所示，发射同步卫星的一般程序是：先让卫星进入一个近地的圆轨道，然后在P点变轨，进入椭圆形转移轨道(该椭圆轨道的近地点为近地圆轨道上的P，远地点为同步圆轨道上的Q)，到达远地点Q时再次变轨，进入同步轨道．设卫星在近地圆轨道上运行的速率为v1，在椭圆形转移轨道的近地点P的速率为v2，沿转移轨道刚到达远地点Q

2016-04-11)