不同颗粒流化床层中挡板受力特性对比
2016-09-18刘对平董芳芳王蒙魏庆张永民
刘对平,董芳芳,王蒙,魏庆,张永民
(中国石油大学(北京)重质油国家重点实验室,北京 102249)
不同颗粒流化床层中挡板受力特性对比
刘对平,董芳芳,王蒙,魏庆,张永民
(中国石油大学(北京)重质油国家重点实验室,北京 102249)
颗粒性质对流化床内气固流动特性具有重要的影响,不同颗粒床层内气固流动特性的不同也将引起床层中内构件受力特性的变化。采用在测试挡板表面粘贴应变计的方法,系统对比测量了一个斜片挡板在 FCC颗粒(Geldart A)和石英砂颗粒(Geldart B)两种流化床内受力特性的差异,并系统比较了操作参数变化时挡板在两种颗粒床层中受力特性变化规律的差异。结果表明,在相同的操作条件下,挡板在B类颗粒床层中受力载荷的均方根值大小约是A类颗粒床层中的2~3倍;除挡板安装在靠近分布器位置外,总体来讲,在两种颗粒的床层中,挡板所受载荷强度都随表观气速的增大而增大。但是,在两种颗粒床层中,挡板安装高度变化对挡板受力特性影响差异较大,在B类颗粒床层中所受载荷强度随着安装高度增大而增大,而在A类颗粒床层中所受载荷强度随安装高度增大呈现先减小后增大的趋势。此外,挡板倾角度θ 在 75°~90°之间变化时,挡板所受载荷强度在两种颗粒流化床中均随着挡板倾角增大呈现急剧下降的趋势,而当θ =0°~75°时,B类颗粒床层中挡板所受载荷强度随挡板倾角增大略有下降,而A类颗粒床层中挡板所受载荷强度变化并不十分明显。
挡板;流化床;受力;颗粒;影响
引 言
流化床反应器高效的传热传质特性使其在石油化工、冶金、燃烧、生化等重要工业生产领域有着十分广泛的应用[1]。为了改善流化床内气固接触效果和强化反应器性能,常通过添加内构件来提升反应器性能[2-5],其中以斜片挡板为基本结构单元的各类内构件应用最为广泛。在众多工业生产过程中,工业装置往往要求在较长检修周期下安全运行,对设备的可靠性要求十分苛刻。由于流化床反应器内复杂的气固两相流动,使得设置在反应器中的内构件会受到气固相持续的冲击作用力,该力可能导致内构件及其支撑结构的振动甚至疲劳破坏。因此,了解不同形式的内构件在不同操作条件下的受力特性规律,对内构件的科学设计和可靠性提高有着重要的意义。
目前,国内外关于内构件受力方面的研究工作还相对较少。Baskakov等[6]较早研究了浸没在气固流化床中的水平圆盘的受力特性,通过考察颗粒类型、圆盘大小、圆盘安装高度等参数对圆盘受力大小的影响,得到了一个能够预测水平圆盘平均受力大小的量纲1关联式。Tamarin等[7]将一直径为5.5 mm的塑料小球安装在二维流化中,通过拍摄的气泡上升的过程和同步采集气泡经过时小球的受力信号,研究了单个气泡与小球作用的受力机理,结果表明,当气泡尾部接触到小球时,小球的受力达到最大。之后,Kennedy等[8-9]对流化床内水平换热圆管受力特性展开了研究,考察了操作气速、圆管排列方式及圆管长度等因素对圆管受力大小的影响。Hosny等[10-11]和 Nagahashi等[12-13]又从圆管直径、颗粒类型、静床高度、圆管间距等方面进一步考察了水平圆管在流化床内的受力规律。此外,Nagahashi等[14]利用在起始流化状态下注入气泡的方法,通过采集圆管的受力信号,并利用高速摄像机拍摄的气泡的上升过程,分析了单个气泡及两个聚并气泡与水平圆管作用的过程,详细阐述了水平圆管的受力机理,该机理与 Tamarin等[7]得到的气泡与小球的作用机理相类似。Levy等[15-16]利用相同的方法,研究了单个气泡及两个聚并气泡与圆管作用时圆管受力信号特征的差异,并提出了一种区分这两种类型气泡作用的方法。
上述研究表明,内构件的受力与床层内颗粒和气泡的流动行为有着密切的关系,而不同颗粒类型床层中气固流动特性差异巨大,必然造成内构件受力特性规律的不同。上文提到的前期文献研究大多是在Geldart B类颗粒中,系统对比颗粒类型对内构件受力特性影响的研究较少[8-11]。另一方面,除本课题组[17]前期一篇对 A类颗粒流化床中悬臂斜片挡板受力特性的报道外,至今对于工业中广泛应用的斜片挡板内构件受力特性的报道还基本没有。本研究的目的是通过实验系统比较两端固定的斜片挡板内构件在Geldart A类和B类两种不同颗粒类型流化床中受力特性的差异和相关性。
1 实 验
1.1实验装置
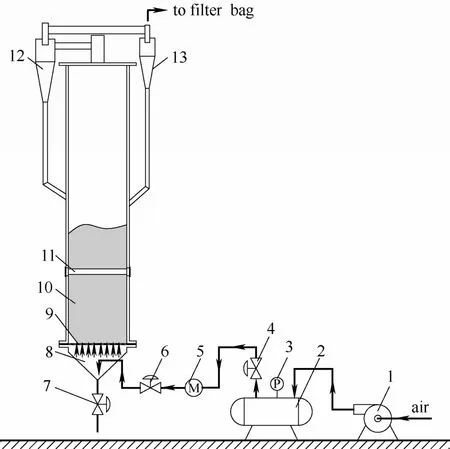
图1 冷模实验装置简图Fig.1 Schematic of experimental unit
实验在一套方形横截面的大型冷模流化床装置中进行,装置结构如图1所示,横截面积为300 mm×300 mm,床高5 m。底部采用多孔板式气体分器,开孔率为0.64%。床内流化气体由一台罗茨鼓风机提供,来自鼓风机的空气首先进入气体缓冲罐,再经管路输送至分布板下方的预分配腔,气体管路上安装有调节阀和数字涡轮流量计来调控气体的流量。进入预分配腔的气体经预混合后经过多孔板分布器均匀分配至床层,为防止细颗粒漏入预分配腔,在多孔板上方加有一层滤网。此外,由于气速较高时,床层内部分颗粒会被气体携带出床层,为保证实验过程中床层内颗粒藏量和粒径分布的一致性,在床层顶部设置有两级PV型旋风分离器来回收这部分颗粒,并及时将其返回到床层密相段。两级旋风分离器的总捕集效率达到99.99%以上,能够保证实验过程中床层内颗粒藏量和粒径分布基本不变。旋风分离器未能捕集的细颗粒由一个滤袋回收,并定期返回至床层中。
实验中静床高度为1 m,且始终保持不变,采用的颗粒为 FCC平衡催化剂和石英砂两种类型颗粒,分别属于典型的Geldart A和Geldart B类颗粒,两种颗粒的基本物性参数见表1。
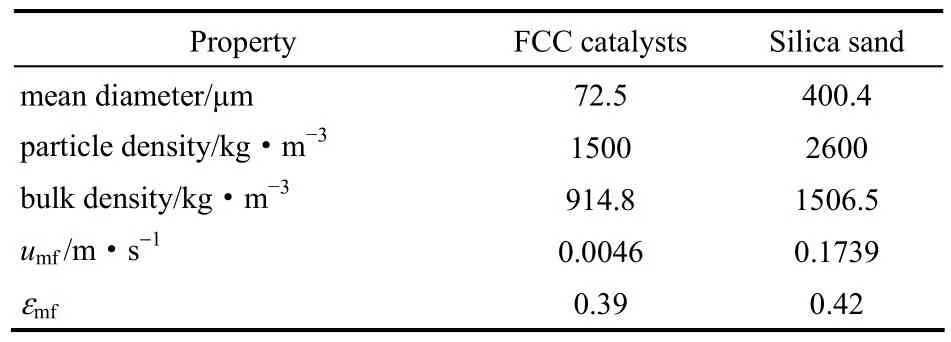
表1 两种颗粒的基本物性参数Table 1 M ajor properties of em p loyed two types of particles
1.2测试挡板及受力特性测量方法
考虑到目前工业应用的很多旨在强化气固接触的挡板内构件都是由斜片挡板作为基本组成单元,因此,设计了如图2所示的测试挡板,该测试挡板由两部分组成,中间斜片用于受力信号的测量,其尺寸为300 mm×50 mm。前期实验表明,在两种颗粒床层中挡板受力大小差别较大,为了保证测试信号的精度,在FCC颗粒床层中,测试挡板厚度选用 2 mm,而在石英砂颗粒床层中,测试挡板厚度选用3 mm,材料都为304不锈钢。两端的圆盘用于将测试挡板两端固定在床层壁面上,且圆盘上开有24个螺纹孔,可以15°间隔实现测试挡板倾斜角度的调节。
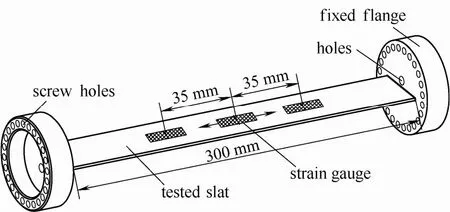
图2 测试挡板示意图Fig.2 Schematic of tested slat
在本研究中,主要考察表观气速、挡板安装高度及挡板倾斜角度3个参数变化的情况下挡板内构件在两种不同颗粒类型床层中受力特性变化规律的差异性。兼顾工业装置的气速操作范围及该装置的具体情况,操作气速范围为0.2~0.8 m·s-1,共设7个气速档;安装高度方面,在床层中心线上设置有5个安装位置,分别距底部分布器为100、300、500、700、900 mm;倾斜角度方面,挡板倾斜角度调节范围为0°~90°,间隔15°调整。在此,倾斜角度定义为挡板表面与水平面之间的夹角。
本实验采用粘贴应变计的方法来测量挡板长度方向所受的张应力大小,挡板表面沿长度方向共粘贴有9个应变计,如图2所示,其中1个布置在挡板中间位置,其余8个应变计以挡板中心线对称分布,分别距离挡板中心线35、70、105、140 mm。应变计引线端经引线孔引出后接入动态应力应变采集系统,应力信号经A/D转换后输入计算机进行显示、记录和输出。应变计为日本Kyowa公司生产的KFG-5-120-C1-11型箔式电阻应变计,应变计大小为5 mm×3 mm,灵敏度系数为2.09(±1.0%)。应力应变采集系统为江苏东华测试的DH5921动态应力应变测试分析系统,其采样频率最大能达到 20 kHz,系统示值误差不大于0.5%。为保证足够高的采样精度,本实验中应力信号的采样频率选用1000 Hz,采样时间为120 s。
1.3数据的分析方法
在流化床中,挡板的受力信号主要来源于气泡的作用,通常表现为一系列脉冲信号。但是,在实际流化床中,由于与挡板作用的气泡个数较多,这些脉冲信号往往叠加在一起,很难单独区分,因此很难确定脉冲的频率和幅值。鉴于流化床挡板内构件的结构设计中(尤其是在疲劳寿命分析中)最为关注的是载荷谱中峰值较大的载荷[18],而并非所有的载荷信号,因为这些峰值较大载荷的作用会对内构件的破坏起到主导作用。因此,如图3所示,通过在张应力脉冲信号上划定一临界值来区分这些峰值较大的载荷,并利用Matlab软件编程求取该临界值之上的张应力脉冲信号的所有峰值,对得到的峰值载荷进行概率密度分布分析。这里,根据对不同操作参数下挡板受到的张应力脉冲信号的特征分析,临界值确定为张应力脉冲信号的平均值与偏差的一半之和,即

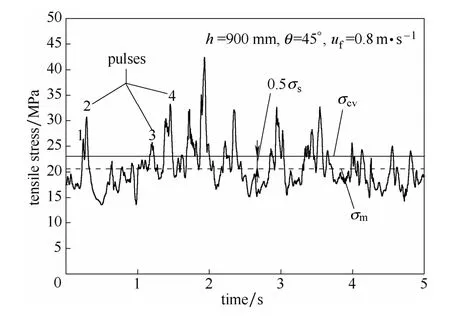
图3 区分张应力脉冲信号中峰值载荷的方法Fig.3 Method of distinguishing tensile stress pulses w ith high peak values
此外,考虑到挡板受到的应力载荷中有正值也有负值,因此,采用张应力脉冲信号的算术平均值来表征挡板在一段时间内受力载荷的强度会出现信号中正负值相抵消的情况,与挡板真实受力载荷会有差别,因此,为了避免这种差别,采用张应力脉冲信号的均方根值来表征挡板在一段时间内受力载荷的强度,之前报道的文献中也采用过相同的表征方法[8-10],其中张应力脉冲信号的均方根值计算公式如下
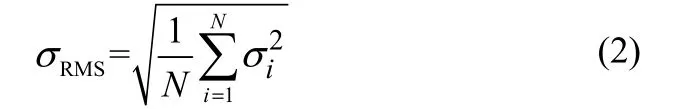
2 实验结果与讨论
2.1挡板张应力分布的对比
图4对比了两种颗粒床层中挡板表面的张应力沿长度方向的分布,可以看出,两种情况下挡板表面测得的最大张应力都出现在最靠近挡板端部的位置。但是,在A类颗粒床层中,挡板中部的张应力大小与端部很接近,而B类颗粒床层中挡板中部的张应力较端部小很多。所以,在挡板的结构设计中,可适当增加挡板端部位置的厚度来提高挡板整体的可靠性。
此外,本研究中测量得到的张应力不仅和流化床内的流动特性有关系,而且也和挡板内构件自身的结构有关,例如,同样操作条件下不同厚度的挡板所测得的张应力是不相同的,因此,应该对测量结果进行适当处理,尽可能剔除挡板结构参数的影响,得到反映床层与挡板相互作用的普适性受力特性结果。

图4 两种颗粒流化床中挡板表面张应力分布的对比Fig.4 Comparison of measured profiles of tensile stress in tested slat in two fluidized beds
如图5所示,对于一个长L、宽a、厚b的两端固定的矩形截面梁,如果梁表面受到一个大小为q的均布载荷,则根据材料力学中两端固定梁的弯矩方程及应力计算公式[19],可求得矩形梁表面上沿长度方向距离A端x位置处的张应力为
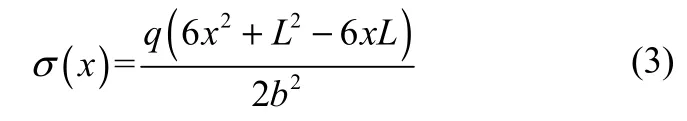
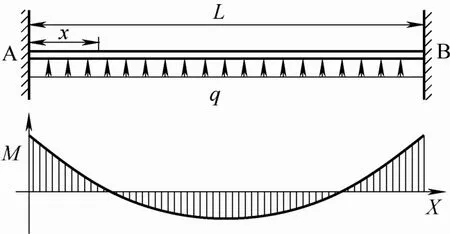
图5 两端固定梁弯矩示意图Fig.5 Bending moment diagram of beam fixed at both ends
将 x=0.01 m和实验测量的最左端测点处的张应力值σ(x=0.01)代入式(3)中,即可求得该应力值下挡板受到的等效均布载荷q。
该均布载荷q是挡板表面单位面积上受到载荷作用力的大小,与测试挡板本身的结构参数无关。而将该值反代入式(3),即可得到该等效均布载荷作用下挡板张应力分布的理论值,图4也给出了利用这种方法得到的两种颗粒流化床中挡板张应力分布的理论曲线。可以看出,实验值和理论值总体分布趋势吻合较好。但是,两者在数值大小方面有所差异,如在A类颗粒床层中,挡板中部位置处张应力的理论值较实测值偏小一些。在本研究中,测量的张应力结果都采用上述方法等效为对应的均布载荷q来表征挡板受到的载荷强度。
2.2挡板受力信号峰值概率分布的对比
利用1.2节给出的张应力脉冲信号峰值识别方法以及2.1节提出的等效均布载荷计算方法,可以将测量的张应力脉冲信号的峰值等效为对应的均布载荷 q,这里,都以最左端测点处测量的张应力脉冲信号为基础进行分析。图6给出了不同操作条件下两种颗粒流化床中测量的张应力脉冲信号的峰值对应的等效均布载荷的概率密度分布。可以看出,总体来讲,A类颗粒床层中挡板受到的等效均布载荷的概率密度分布更集中,较大载荷出现的概率很小。而相比之下,在B类颗粒床层中,等效均布载荷的分布要更分散一些。
在图6(a)、(b)反映了表观气速对等效均布载荷概率密度分布的影响,可以看出,随着表观气速的增大,在两种颗粒床层中,q的概率密度分布曲线之间的重合区域变大,载荷的分布范围更接近。
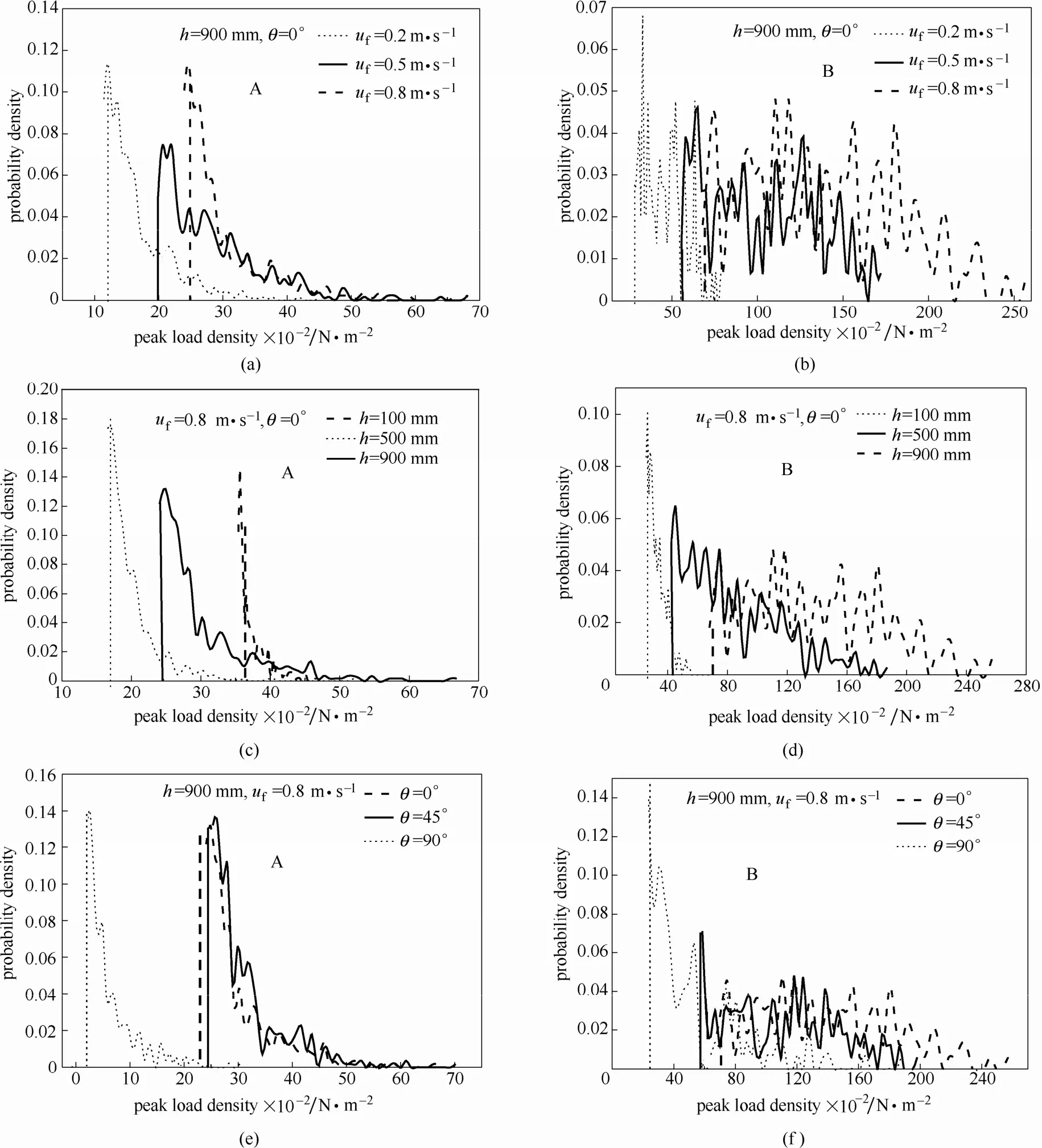
图6 两种颗粒床层中挡板受到等效均布载荷概率密度分布的对比Fig.6 Comparison of probability density of peak uniform load in two fluidized beds
图6(c)、(d)反映了挡板安装高度对等效均布载荷概率密度分布的影响,可以看出,在A类颗粒床层中,不同安装高度下对应的q的概率密度分布曲线偏移较大,重叠区域很小,且在B类颗粒床层中,挡板安装在靠近分布器的位置时,q的概率密度分布也呈现很好的集中性。
图6(e)、(f)反映了挡板倾斜角度对等效均布载荷概率密度分布的影响,对比两图可以看出,在两种颗粒床层中,挡板倾斜角度为0°和45°时,q的概率密度分布曲线很相似。这也说明,挡板倾角从0°调整至 45°后,挡板受到的张应力脉冲信号的差异并不明显。
2.3表观气速的影响
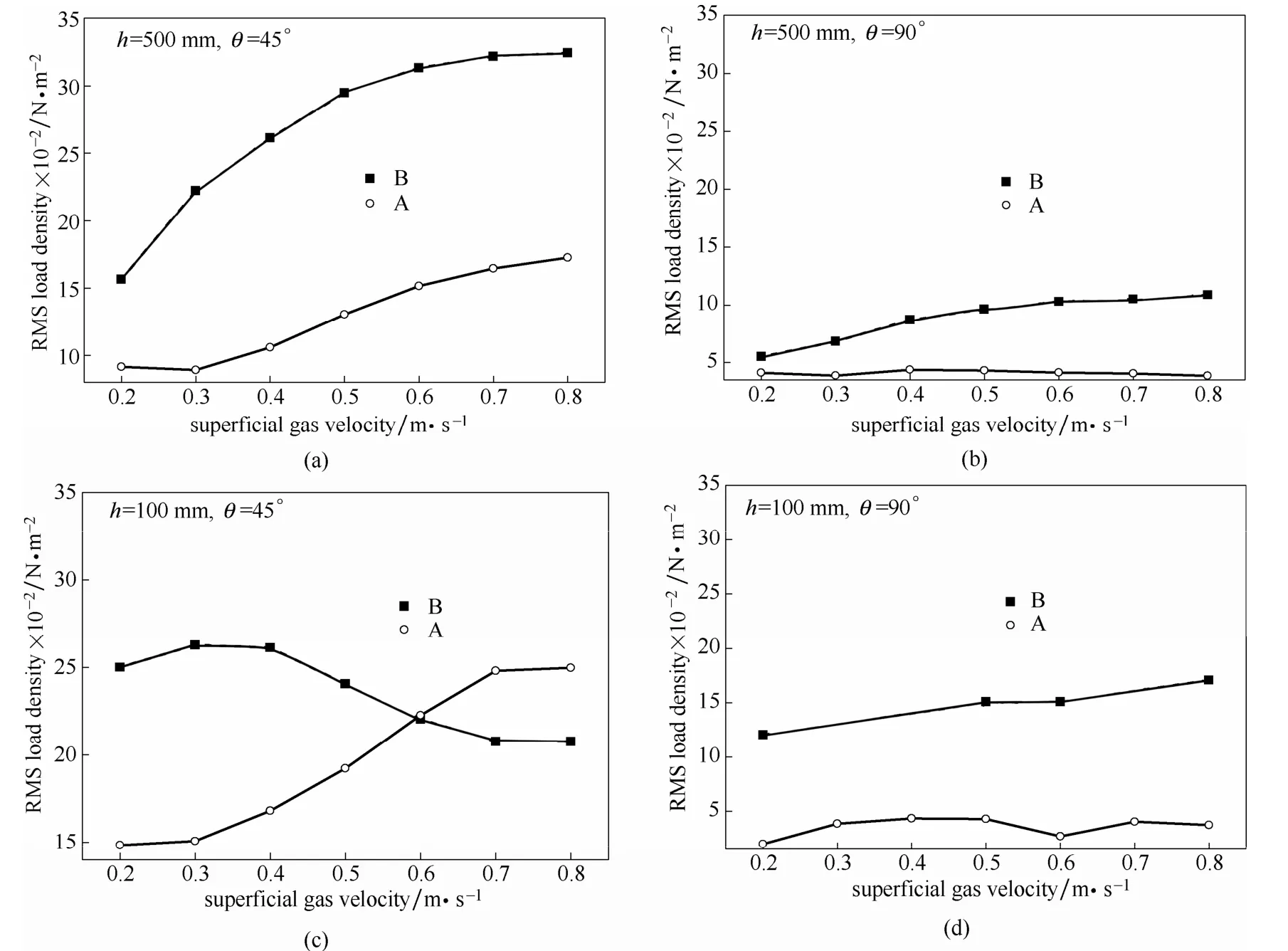
图7 两种颗粒床层中表观气速对挡板受力影响的对比Fig.7 Comparison of effects of superficial gas velocity in two fluidized beds
这里,采用最左端测点处测量的张应力脉冲信号的均方根值对应的等效均布载荷来表征床层内挡板受到气固相作用力的强度,同样,利用2.1节提出的等效均布载荷计算方法进行计算。图7中进一步对比了两种颗粒床层中挡板所受的等效均布载荷强度随表观气速的变化,总体来讲,如图7(a)所示,在A、B类颗粒床层中挡板的受力载荷都随表观气速的增大而增大,且在B类颗粒床层中挡板的受力载荷随气速增大的幅度更大一些,载荷强度约是A类颗粒床层中的 2~3倍。Nagahashi等[14]和 Levy等[15-16]在二维流化床中对换热圆管的受力机理研究表明,气泡尾涡夹带的颗粒的撞击是水平圆管在流化床内受力的主要原因,与水平圆管受力相类似,浸没在床层中的斜片挡板同样也会受到气泡尾涡夹带颗粒的撞击作用力。而随着表观气速的增加,床层内气泡聚并的趋势增强,床内气泡平均尺寸变大,从而使气泡的上升速度增大,尾涡夹带颗粒增多,最终导致气泡尾涡夹带颗粒对挡板的撞击作用力不断增强。另一方面,随着表观气速的增加,床层内气泡数量也在增多,使得与挡板作用的气泡数量同样增加,这也是造成挡板受力载荷增大的另一个原因。此外,相比于A类,B类颗粒床层内气泡的聚并更加严重,气泡平均直径较大,上升速度更快,且从表1中可以看出,B类颗粒的颗粒密度也远大于A类颗粒,这些因素的综合作用造成了挡板在B类颗粒床层中受到相对更大的颗粒冲击作用力。但是,如图 7(b)所示,在挡板倾角为 90°时,在两种颗粒床层中挡板的受力载荷随表观气速增大的幅度很小。这是因为在该角度下,挡板在垂直方向的受力面积很小,气泡尾涡夹带颗粒对挡板的冲击作用力接近于 0,挡板仅受到了水平方向颗粒的挤压作用力。
此外,如图7(c)、(d)所示,挡板安装在靠近分布器位置时,在B类颗粒床层中,挡板的受力载荷在气速达到0.4 m·s-1后呈现下降的趋势,且在挡板倾角为 90°时,挡板在该区域内受力载荷强度相比在床层中部有明显增大,这与其在A类颗粒床层中的受力变化有很大的不同。这种差异说明,在两种颗粒床层中,该区域内气固相对挡板的作用力有着很大的区别,而分布器产生的不同射流的影响可能是造成这些差异的主要原因。
2.4挡板安装高度的影响
图8比较了两种颗粒床层中挡板安装高度变化对挡板受到的载荷强度的影响。可以看出,在A类颗粒床层中,挡板的受力载荷随安装高度增大呈现先减小后增大的趋势,挡板安装在床层中部位置时整体受力载荷较小,而在靠近料面和分布器位置处的受力载荷较大且很接近。在B类颗粒床层中,除在靠近分布器的位置略有下降外,挡板的受力载荷随安装高度的增大接近于线性增加,且在床层料面处挡板的受力载荷是靠近分布器位置的3倍之多。引起这种变化差异的主要原因是在两种颗粒床层中,沿床层高度方向气泡尺寸变化的不同,在A类细颗粒床层中,气泡上升过程中聚并的趋势较弱,且乳相黏度小,气泡最大稳定尺寸小,达到一定床层高度后,床层内气泡直径基本保持不变,床内气泡小而均匀。因此,挡板受到的载荷强度除在分布板影响区和料面附近较大外,在床层中部位置变化很小。而在B类粗颗粒床层中,气泡的聚并严重,气泡长大很快,且气泡的最大稳定尺寸较大,气泡平均直径沿床层高度增加而增大,从而导致气泡尾涡夹带颗粒对挡板的作用力随床层高度增加呈现明显的增大趋势。总之,在挡板设计过程中,一定要考虑这种由颗粒不同引起的挡板受力载荷沿床层高度方向变化规律的差异,对安装在不同反应器内的斜片挡板内构件做出更加科学合理的设计。
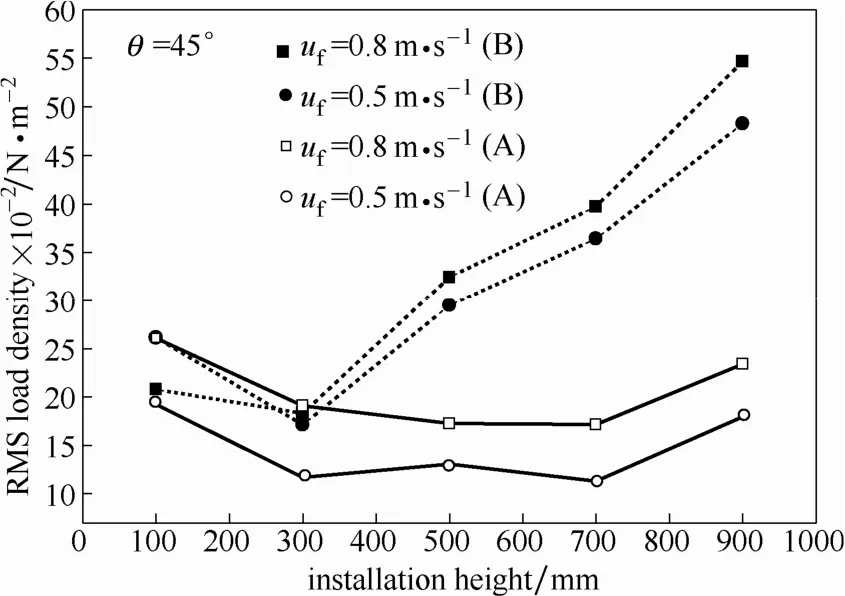
图8 两种颗粒床层中挡板安装高度对挡板受力影响的对比Fig.8 Comparison of effects of installation height in two fluidized beds
2.5倾斜角度的影响
图9比较了在两种颗粒床层中挡板倾斜角度变化对挡板受力载荷强度的影响。可以看出,在B类颗粒床层中,挡板的受力载荷随倾斜角度的增大而减小,且在倾斜角度为 0°~75°范围内,受力载荷的减小趋势平缓一些。而在A类颗粒床层中,挡板的受力载荷随倾斜角度的变化并没有呈现明显的规律性,但总体来讲,倾斜角度在 0°~75°范围内变化时,挡板受力载荷的大小相差很小,而在 75°~90°范围内,挡板的受力载荷出现明显下降。这些差异也说明,相比之下,在A类颗粒床层中,挡板倾斜角度变化对挡板受力载荷强度的影响并没有在B类颗粒床层中明显。因此,对于应用于B类颗粒流化床反应器内的斜片挡板内构件,在不影响内构件性能的条件下,可以考虑通过适当增大斜片的倾斜角度来降低内构件在床层中的受力载荷强度。

图9 两种颗粒床层中挡板倾斜角度对挡板受力影响的对比Fig.9 Comparison of effects of inclination angle in two fluidized beds
2.6挡板受力载荷强度的经验关联式
本研究基于实验数据及结合文献中对流化床内水平圆盘受力的量纲1经验关联式分析[6],给出了斜片挡板在自由床内平均受力载荷强度大小的经验关联式,对于安装在流化床内的斜片挡板,挡板的受力大小主要受到以下因素的影响:床层宽度l,表观气速uf,颗粒密度ρp,颗粒直径de,挡板安装位置距底部分布板距离h,挡板的安装倾斜角度θ ,重力加速度 g。所以定义挡板平均受力载荷强度的函数形式为
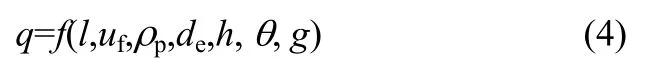
将各参数进行量纲1化后可以得到以下形式
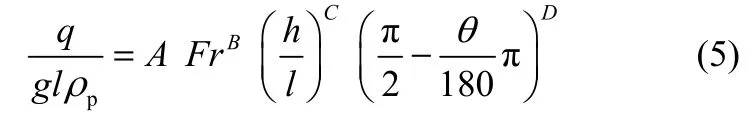
根据实验测量的挡板在两种颗粒床层中的平均受力载荷强度,利用线性拟合的方法,对挡板在A、B类颗粒床层中平均受力载荷强度进行经验关联,在A类颗粒床层中,量纲1准数关联式的表达形式如下
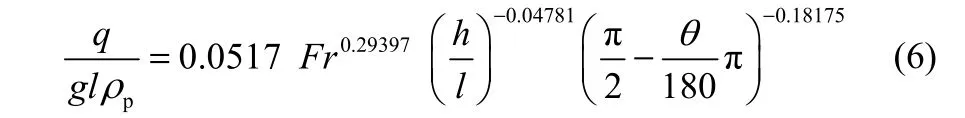
根据本实验操作条件,上述特征数关联式(6)适用范围为:Fr=56~900,h/l=0.3~3,θ =0°~90°。
在B类颗粒床层中,特征数关联式的表达式如下
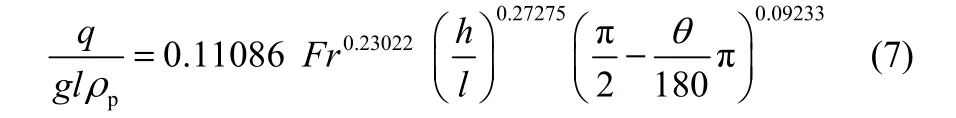
根据本实验操作条件,上述特征数关联式(7)的适用范围为:Fr=10~163,h/l=0.3~3,θ =0°~90°。
将式(6)、式(7)计算的挡板在两种床层中受力载荷强度与实验值进行了比较,如图10所示。可以看出,在两种床层中,多数情况下,计算值与理论值之间吻合较好,但出现在一些操作条件下,实验值与理论值会出现较大的偏差情况,且相比较而言,在A类颗粒床层中,经验关联式对挡板受力强度预测更准确一些。因此,以上经验关联式可以对两种床层内挡板的受力载荷强度做出一定的估算,供挡板设计参考使用,但是不能直接用于工业挡板的设计。
3 结 论
(1)在A类颗粒床层中,挡板测量的张应力脉冲信号中峰值载荷的概率密度分布更集中,而在B类颗粒床层中,挡板测量的张应力脉冲信号中峰值载荷的概率密度分布则比较分散。
(2)总体上,相同操作条件下挡板在B类颗粒床层中所受的载荷强度约是A类颗粒床层中的2~3倍。
(3)除靠近分布器区域外,两种颗粒床层中挡板所受的载荷强度总体上均随表观气速的增大而增大。

图10 两种颗粒床层中挡板平均受力载荷强度计算值与实验值比较Fig.10 Comparison of calculated and measured load densities in two fluidized beds
(4)在两种颗粒床层中,挡板安装高度对挡板受力特性的影响差异很大,B类颗粒床层中挡板的受力载荷随着安装高度增大而增大,而在A类颗粒床层中挡板的受力载荷随安装高度增大呈现先减小后增大的趋势。
(5)在θ =0°~75°时,B类颗粒床层中挡板的受力载荷随挡板倾角增大略有下降,而A类颗粒床层中挡板受力载荷变化不大,但在θ =75°~90°时,两种颗粒床层中挡板受力载荷均随挡板倾角增大急剧下降。
符号说明
a——挡板宽度,mm
b——挡板厚度,mm
Fr——Frendrich数
h——挡板距底部分布板的距离,mm
L——挡板的长度,mm
l——床层宽度,mm
M——挡板沿长度方向弯矩分布,N·m
q ——挡板表面受到的等效均布载荷,N·m-2
qcal.——经验关联式计算的挡板受到的等效均布载荷,N·m-2
qexp——实验测量的挡板受到的等效均布载荷,N·m-2
uf——表观气速,m·s-1
um f——起始流化速度,m·s-1
x ——挡板表面某点距左端A处的距离,m
εm f——起始流化状态下的空隙率
θ ——挡板的倾斜角度,(°)
σ(x) ——挡板表面距离左端x位置处的张应力,MPa
σcv——区分张应力脉冲信号中峰值载荷的临界值,MPa
σi——张应力脉冲信号的瞬时值,MPa
σm——张应力脉冲信号的算术平均值,MPa
σRMS——张应力脉冲信号的均方根值,MPa
σs——张应力脉冲信号的标准偏差值,MPa
References
[1] KUNII D, LEVENSPIEL O. Industrial Application of Fluidized Beds [M]// Fluidization Engineering. 2nd ed. USA: Butterworth-Heinmann,a division of Reed Publishing Inc., 1991: 15-58.
[2] 吴占松, 马润田, 汪展文. 流态化基础及应用[M]. 北京: 化学工业出版社, 2006: 39-41.
WU Z S, MA R T, WANG Z W.Fluidization Technology Foundation and Application [M]. Beijing: Chem ical Industry Press,2006: 39-41.
[3] 陈甘棠, 王樟茂. 流态化技术的理论和应用[M]. 北京: 中国石化出版社, 1996: 124-134.
CHEN G T, WANG Z M. Theory and Application of Fluidization Technology [M]. Beijing: China Petrochem ical Press, 1996: 124-134.
[4] 金涌, 余芷青, 张礼, 等. 流化床脊形内构件[J]. 石油化工, 1986,15(5): 269-277.
JIN Y, YU Z Q, ZHANG L, et al. Ridge type internal baffle for fluidized bed reactor [J]. Petro. Chem. Eng., 1986, 15(5): 269-277.
[5] DUTTA S, SUCIU G D. An experimental study of the effectiveness of baffles and internals in breaking bubbles in fluid beds [J]. J. Chem. Eng., 1992, 25(3): 345-348.
[6] BASKAKOV A P, M ICHKOVSKII B A. Vertical forces acting on horizontal disks in a fluidized bed [J]. Journal of Engineering Physics,1974, 27(6): 1464-1466.
[7] TAMARIN A I, LIVSHITS Y E, GALERSHITEIN D M, et al. Forces acting on a body in a non-uniform fluidized bed [J]. Journal of Engineering Physics, 1977, 32(2): 270-274.
[8] KENNEDY T C, DONOVAN J E, TRIGAS A. Forces on immersed tubes in fluidized beds [J]. AIChE J., 1981, 27(3): 351-357.
[9] DONOVAN J E. A study of forces on simulated heat exchange tubes immersed in a cold fluidized bed [D]. US: Oregon State University,1980.
[10] HOSNY N M. Forces on tubes immersed in a fluidized bed [D]. Canada: The University of British Columbia, 1982.
[11] HOSNY N M, GRACE J R. Transient forces on tubes w ithin an array in a fluidized bed [J]. AIChE J., 1984, 30(6): 974-976.
[12] NAGAHASHI Y, GRACE J R, LIM K S, et al. Dynam ic force reduction and heat transfer improvement for horizontal tubes in large-particle gas-fluidized beds [J]. J. Therm. Sci., 2008, 17(1): 77-83.
[13] NAGAHASHI Y, YAMAMOTO D, GRACE J R, et al. Forces on horizontal tubes of non-circular cross-section in fluidized beds [C]// The 14th International Engineering Conference on Fluidization: From Fundamentals to Products. Netherlands, 2013.
[14] NAGAHASHI Y, ASAKO Y, LIM K S, et al. Dynam ic forces on a horizontal tube due to passing bubbles in fluidized beds [J]. Powder Technol., 1998, 98: 177-182.
[15] LEVY E K, WAGH M, SETHU H, et al. Pattern recognition analysis of bubbles impacting on tubes [J]. Powder Technol., 1992, 70: 175-181.
[16] LEVY E K, AYALON A, JOHNSON S, et al. Dynam ic loading on a horizontal tube in a bubbling fluidized bed [C]//Annual Meeting of the America Institute of Chem ical Egineerings: Fluidized Processes: Theory and Practice. USA: Publication of AIChE, 1992: 99-106.
[17] 王若艺, 刘对平, 李智, 等. 细颗粒气固流化床内斜片挡板受力特性的实验研究[J]. 过程工程学报, 2015, 15(3): 375-380.
WANG R Y, LIU D P, LI Z, et al. Experimental study on the force characteristics acting on the slat baffles in fine particles gas-solids fluidized bed [J]. CJPE Journal, 2015, 15(3): 375-380.
[18] 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2001: 32-37.
CHEN C Y. Fatigue and Fracture [M]. Wuhan: Huazhong University of Science and Technology Press, 2001: 32-37.
[19] 熊有得. 材料强度力学[M]. 北京: 科学技术出版社, 2009: 290-291.
XIONG Y D. Mechanics of Material Strength [M]. Beijing: Science Press, 2009: 290-291.
Com parison of force characteristics in two fluidized beds w ith different particles
LIU Duiping, DONG Fangfang, WANG M eng, WEI Qing, ZHANG Yongm in
(State Key Laboratory of Heavy Oil Processing, China University of Petroleum, Beijing 102249, China)
Particle properties have significant effect on gas/solids flow characteristics, which results in significantly different force characteristics exerted in the internals immersed in fluidized beds of different particles. In this study, the dynamic force in a tested slat immersed in fluidized bed was measured by adhering strain gauges on its surface. The force characteristics of the slat were systematically compared in two beds of FCC catalyst particles (Geldart A) and silica sand particles (Geldart B). The experimental results showed that the RMS load density acting on the slat in the bed of Geldart B particles was about 2—3 times higher than in the bed of Geldart A particles. Except installed near the bottom distributor, the measured load density on the slat increased w ith increasing superficial gas velocity in both beds. However, the effect of the installation height of the slat indicated great difference in the two beds. The measured load density on the slat increased w ith increasing installation height in the bed w ith Geldart B particles, while it decreased firstly and then increased w ith increasing installation height in the Geldart A particles bed. At θ =75ο—90ο, the measured load densities decreased sharply w ith increasing inclination angle in both beds. However, at θ =0ο—75ο, the measured load density decreased slightlyw ith increasing inclination angle in the bed of Geldart B particles, while there was no obvious change in the bed of Geldart A particles.
slat; fluidized bed; force; particle; effect
date: 2016-03-25.
Prof. ZHANG Yongmin, zym0876@gmail. com
supported by the National Basic Research Program of China (2012CB215004), the National Natural Science Foundation of China (21276273) and the Science Foundation of China University of Petroleum, Beijing (2462015YQ0312).
TQ 028.8
A
0438—1157(2016)08—3331—09
10.11949/j.issn.0438-1157.20160345
2016-03-25收到初稿,2016-05-13收到修改稿。
联系人:张永民。第一作者:刘对平(1991—),男,博士研究生。
国家重点基础研究发展计划项目(2012CB215004);国家自然科学基金项目(21276273);中国石油大学(北京)科研基金项目(2462015YQ0312)。