冲击信号零漂修正的冲击响应谱互相关系数分析
2016-09-18李海广潘宏侠任海锋
李海广 , 潘宏侠, 任海锋
(1.中北大学 机电工程学院,太原 030051; 2.内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室,包头 014010)
冲击信号零漂修正的冲击响应谱互相关系数分析
李海广1,2, 潘宏侠1, 任海锋1
(1.中北大学 机电工程学院,太原030051; 2.内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室,包头014010)
冲击振动信号通常因为冲击能量强、传感器特性等因素的影响,存在基线漂移现象,进而影响到后续的数据分析处理。针对这一问题,首先通过计算冲击信号的冲击响应谱,提出正负冲击响应谱互相关系数的定义,利用互相关系数开展检测基线漂移程度、检验修正效果等工作;其次,提出利用响应谱互相关系数为重构条件的自适应经验模式分解(EMD)漂移修正新方法,并与其他方法进行了比较。在对某机枪自动机动作过程中的冲击振动基线漂移信号分析和验证,数据结果表明,冲击响应谱互相关系数较传统的响应谱低频斜率等响应谱特征值,更能准确有效的表征基线漂移程度、以及修正效果的评判。
基线漂移;冲击响应谱; 互相关系数;经验模式分解
冲击振动信号在测量过程中往往出现基线漂移现象,影响到测量精度,甚至数据的获取。基线漂移产生的主要原因是测量传感器在高冲击下产生的失效特性[1-2],如压电式加速度传感器的零漂现象[3-4]。对于基线漂移的数据最理想的处理是弃之不用[5],然而往往受到测量环境、测量设备等条件限制,测量数据具有唯一性[6],促使学者研究一些修正方法去除基线漂移,如采用小波分解的方法[5,7],EMD方法[8]等。然而对于冲击信号基线漂移的研究内容中,还有两个基本问题没有解决,如何度量基线漂移程度、如何比较修正方法。对于这两个问题的研究中,冲击响应谱是一种很好的工具,冲击响应谱的最大响应谱、速度谱及正负响应谱都涉及到冲击信号的对称性,已经有学者研究表明在双对数坐标下最大响应谱低频直线段斜率应满足在6 dB/oct与12 dB/oct之间,低于6 dB/oct则存在基线漂移[9],正负谱在某些频率的差值应小于6 dB/oct,否则存在基线漂移[10]。笔者在自动武器的自动机动作冲击振动信号处理过程中,同样遇到基线漂移的问题,经过研究比较,本文提出正负冲击响应谱互相关系数的定义,利用互相关系数可以量度冲击信号的基线漂移程度;提出利用互相关系数为重构条件的EMD自适应漂移修正方法,同样可以利用互相关系数比较不同的漂移修正方法的修正效果。试验数据表明响应谱互相关系数可以有效的量度偏移程度及比较修正方法的效果。
1 理论基础
1.1冲击响应谱
冲击响应谱是基于冲击加速度历史数据的计算函数,主要思想是将冲击激励施加在一个标准的单自由度的质量弹簧阻尼振动系统,如图1所示,每个单元由质量为mi的质块,刚度为ki的弹簧,和一个阻尼为ci的阻尼器组成的单自由度系统,每个单元系统阻尼比ξ是相等的,冲击加速度数据作为输入信号,作用在系统基础上,得到的每个质块的加速度响应,并将最大加速度响应Gi作为质块自然频率ωi的函数构成冲击响应谱。

图1 冲击响应谱原理示意图Fig.1 Shock response spectrum model
将加速度信号作为基础激励源,质块的运动方程:

(1)
式中:x为质块的绝对位移,y为基座的位移,定义z=x-y为相对位移,式(1)转化为
(2)

求解式(2),可以得到冲击响应峰值与自然频率之间的函数,即该系统的冲击响应谱。目前应用较广泛的冲击响应谱算法是改进的递归数字滤波法[11],该方法于由SMALLWOOD[12]提出来。
根据冲击作用时间,响应谱可以分为初始响应谱、残余响应谱;同时根据响应参变量矢量方向,响应谱可以分为正谱和负谱,正负谱可以反映出冲击系统的对称性,每时刻正负谱的绝对峰值谱作为系统的最大响应谱,图2为各响应谱的关系图。

图2 不同冲击响应谱关系图Fig.2 Links between the different definitions of SRS

图3 不同频率的正弦冲击激励信号Fig.3 Different shape on symmetric impact signal
1.2基线漂移的冲击响应谱特征提取
冲激响应谱能够反映冲击信号对称性关系,图3(a)~(f)分别为频率为50 Hz、100 Hz、200 Hz,400 Hz、600 Hz、800 Hz正弦冲击信号,采样频率为10 000 Hz,采样时长为0.03 s,其中冲击信号时间间隔为0.01 s,形成不同对称程度的冲击信号。
分别计算各冲击信号的冲击响应谱,其中冲击响应谱计算参数为:自然频率初始值10 Hz,最大自然频率的选择采集频率的1/8、倍频为21/6,即自然频率序列为10,10.595,11.225,11.892,…,100×21/6(N-1),这里N=85;阻尼比ξ= 0.05,响应谱的计算采用递归数字滤波法。
图4为图3正弦冲击信号的最大冲击响应谱,从图中可以发现,不同对称形式的冲击信号,所对应最大冲击响应谱不同。一般最大冲击响应谱可以划分为三个区域[13]:脉冲区域(impulse domain),响应谱幅值小于冲击幅值区域;静态区域(static domain) ,响应谱幅值在高频区域趋向于冲击幅值的区域;中间区域(intermediate),响应谱峰值是冲击幅值动态放大,放大系数显著的依赖于冲击的形状和系统的阻尼。图4中各响应谱线在对数坐标下的直线段位于脉冲区域,该区域的斜率在6 dB/oct与12 dB/oct之间[9],比较小的斜率是由于传感器缺陷产生基线漂移造成的,同时PIERSOL[10]认为由于背景噪音造成斜率小于6 dB/oct的冲击信号是无效的。如图所示,半波正弦函数谱线直线段的斜率明显小于其他对称正弦冲击信号谱线。

图4 不同冲击激励对应的最大响应谱Fig.4 Max shock response spectrum of different impact vibration signals
正负响应谱同样可以反映出冲击信号的对称性,图5为图3冲击激励信号的正负响应谱,图中半波正弦信号正负谱线明显不同,但随着冲击信号对称性增强,正负谱线趋于重合。为进一步定量衡量谱线重合度,本文定义正负响应谱线的互相关系数。
(3)
式中:Cov(SRS+,SRS-)为正负响应谱互相关函数,Var(SRS+)、Var(SRS-)为正负响应谱方差,分别计算系列冲击激励的正负谱线互相关系数,如图6(a)所示,互相关系数除半坡正弦冲击较低外,其余冲击信号逐渐增大趋于一稳定值,同时计算响应谱低频段斜率,图6(b)中,系列冲击信号响应谱斜率逐渐减小并趋于一稳定值,说明对于本文采用的系列正弦冲击激励信号,冲击响应谱互相关系数同样具有指示激励信号对称性的作用,可以反映基线漂移程度,而且相关系数是取值0~1之间的相对值,较正负谱具体差值方法[10]更有利于比较,同时由于随着信号对称性增强,相关系数趋于稳定值,可以根据信号特性设置相关系数有效阀值,相关系数在阀值之上可以认为信号基线漂移程度符合要求。
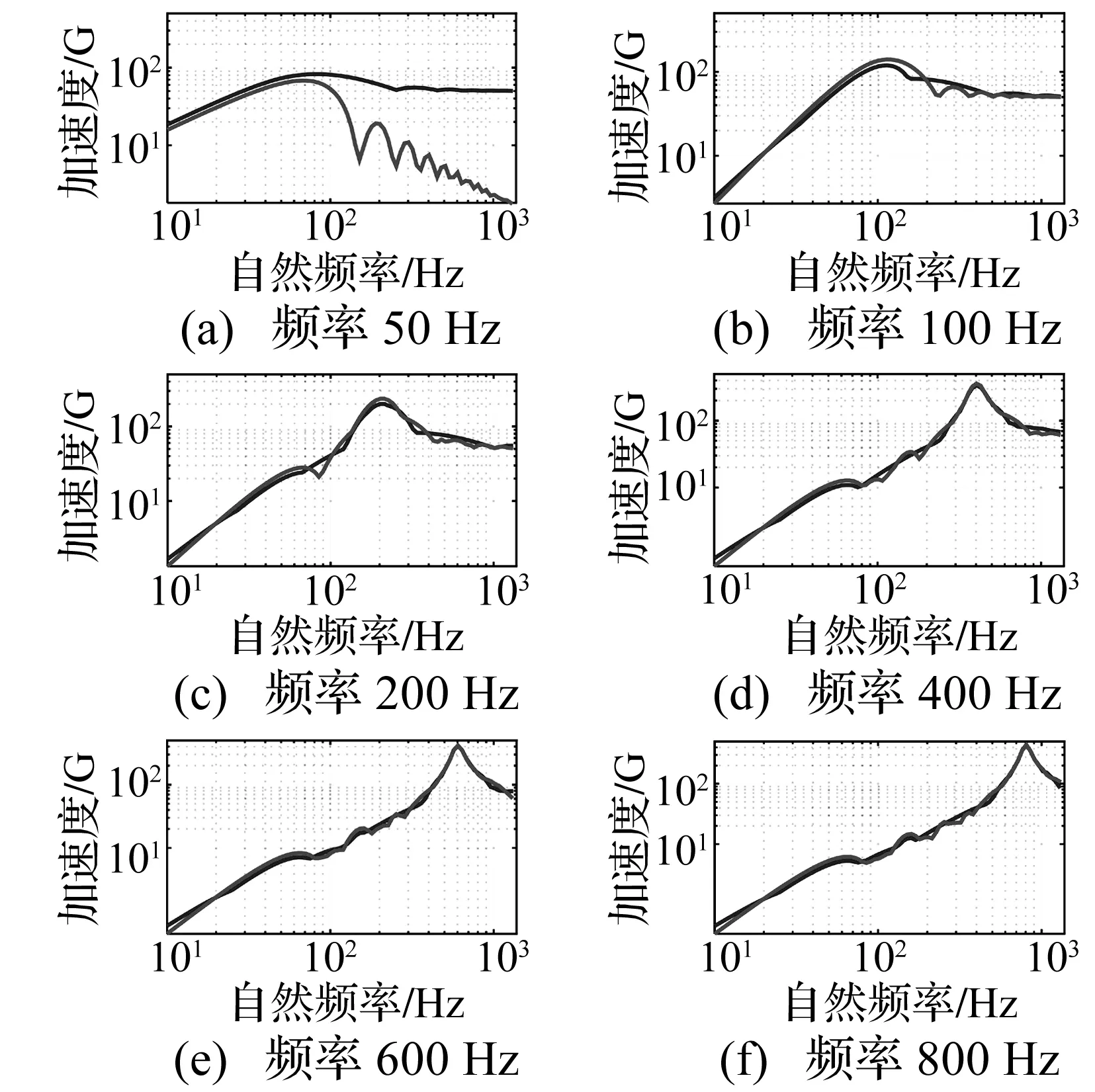
图5 不同冲击激励对应正负响应谱Fig.5 Maximax shock response spectrum of different impact vibration signals

图6 不同冲击激励冲击响应谱特征提取Fig.6 Shock response spectrum features extraction from different impact vibration signals
1.3基线去除方法
目前,去基线漂移的滤波算法已经比较多,比如基于平滑滤波器的滤波算法,五点三次算法、形态滤波算法,基线拟合算法等,还有基于信号分解,将低频分量分离消除基线漂移的滤波算法,如小波变换、EMD等,本文分别列举五点三次算法、小波算法和EMD算法基本原理。
(1) 五点三次平滑算法
五点三次平滑算法是等间距数值基础上的一种局部平滑的方法,在五点的局部数据窗口内,采用三次多项式拟合,确定加权平均系数,利用数据窗口对所有数据点进行平滑处理后,即平滑1次。在进行多次平滑后,可以有效消除数据的毛刺,得到数据光滑的趋势项,如果将原数据减去趋势项后,即可得到信号的高频成份,所以五点三次平滑算法可以用于基线漂移的去除。
(2) 小波算法
利用小波变换多尺度多分辨率的特点,将信号进行多尺度小波分解。由于基线漂移的主要成分为缓变趋势分量,在小波分解中会直接显现于较大的尺度下,只要在重构过程中将这一尺度下的分量直接去除,便可以实现基线漂移的修正。
(3) EMD分解去基线
EMD分解[14]是由黄锷博士提出的一种非线性信号分析方法,其原理为根据时间尺度特征对于信号进行分解,将复杂信号分解为有限个本构函数(IMF),本构函数包含了相应时间尺度局部信号特征,每个IMF为满足以下两个条件的局部信号:① 函数在整个时间范围中,局部极值点和过零点的数目相同,或者是最多相差一个;② 在任意时间点,局部最大值包络(上包络线)以及局部最小值的包络(下包络线) 平均值是零。
EMD分解结果为:原信号x(t) 可表示为级若干IMF分量和一个趋势项之和,如式(4)表示。
(4)
每个IMF为一个单一频率范围。EMD分解本质上具备高通滤波特征,可以将IMF由高频到低频依次的分解出来,而基线漂移是叠加在信号上的低频分量,因此将低频IMF去除后重构信号即可完成基线漂移的消除。
2 试验数据分析
2.1自动机动作冲击信号的获取
(1) 自动机冲击振动试验装置
本文试验采用某高射机枪自动机,该自动机为导气式自动机,其工作原理为利用弹药在枪管内的高温高压燃气推动活塞,由自动机构完成弹药的击发、击发复位、开锁、开闩、抽筒等循环过程。考虑到自动机主要动作构件及传感器安装条件因素,测点布置如图7所示,测点1为枪尾上方,测点2为机匣左侧冲击振动信号由三向压电加速度传感器获得,经放大后由便携式DASP采集系统记录,采集频率为51.2 kHz,生成2个测点位置3个不同方向的6组冲击加速度信号,数据模式根据射击模式不同,可分为单发、三连发、五连发数据,相关传感器参数可由表1获得。

图7 试验机枪及测点分布Fig.7 Gun test and measurement point distribution

测点位置灵敏度/(pC·ms-2)XYZ型号测点1枪尾上方23.021.819.0CA-YD-116测点2机匣左侧18.221.820.8CA-YD-116
(2) 冲击振动信号的基线漂移
图8为单发射击模式下的冲击振动时域图,由振动信号可以看出,信号具有很强的冲击特性,能量在撞击后出现峰值,之后迅速地衰减,而每一次撞击正是完成自动机动作过程中的一环节。冲击振动信号包含了自动机工作时正常高频振动信号,但也存在低频的漂移干扰信号,如图中1z,2z方向,产生的原理主要有,传感器在剧烈冲击振动中,进入非线性工作区,以及传感器固定装置产生松弛等原因。低频漂移并未携带有用信息,同时会给后续的信号特征提取带来不便,因此有必要去除基线漂移信号。

图8 两测点不同方向的冲击信号Fig.8 Signals at each measurement point from different directions
(3) 基线漂移的冲击响应谱分析
观察图8中的冲击振动信号可以发现:测点1的z方向冲击信号基线漂移比较严重,其他信号也存在不同程度的基线漂移。根据上文分析,可以通过计算冲击响应谱提取响应谱特征来定量的比较,计算相应响应谱如图9所示,最大响应谱低频段斜率为4.821 6 dB/oct,正负谱线显示出明显的差异,其互相关系数为0.270 32。

图9 基线漂移的冲击响应谱分析Fig.9 Shock response spectrum analysis for baseline shift
计算并比较所有测量信号的冲击响应谱特征值,图10为计算结果,其中,根据PIERSO的分析,测点1x、2x方向的响应谱低频斜率大于6 dB/oct,冲击信号有效,其它方向均小于6 dB/oct,信号存在基线漂移,但从图中可以发现,1z方向的低频斜率并不是最小,表明低频斜率特征值并不能用于漂移程度的比较;相反,正负谱线互相关系数可以量化漂移程度的不同,各测点相关系数依次为0.983 246、0.991 672、0.270 32、0.989 849、0.990 441、0.936 797,如图10(b)所示,其中1z方向0.270 3明显低于其它方向,而且除1z测点外,2z方向相关系数0.936 797也低于其它测量值,根据观察可以设置冲击信号有效阀值为0.990 00,同时相关系数的比较关系完全符合图8的观察结果。

图10 测量冲击信号基线漂移响应谱特征值比较Fig.10 Comparison chart of shock response spectrum features for impact signals
2.2基线漂移的修正效果比较
(1) 五点三次平滑漂移修正
利用五点三次平滑算法对测点1的z方向冲击信号平滑1 000次,得到趋势项后,计算原信号与趋势项的差值得到漂移修正信号,并计算冲击响应谱,如图11所示,其中最大响应谱低频段斜率为6 dB/oct,正负谱线互相关系数为0.998 861,而且从图中可以看出正负谱线几乎完全重合,说明趋势项已经很大程度上被消除。

图11 五点三次平滑漂移修正的冲击响应谱分析Fig.11 Shock response spectrum analysis for baseline correction using five-spot triple smoothing algorithm
(2) 基于小波漂移修正
采用离散Meyer小波,将测点1的z方向冲击信号,进行10尺度小波分解,提取第10尺度上的低频小波分解系数,即趋势项系数,将系数置零后重构冲击信号,并计算冲击响应谱,如图12所示。其中最大响应谱低频段斜率为6.045 dB/oct,正负谱线互相关系数为0.881 497,而且从图中可以看出正负谱线部分重合,说明趋势项并没有被完全消除。
图12 小波漂移修正的冲击响应谱分析Fig.12 Shock response spectrum analysis for baseline correction using wavelet algorithm
(3) 基于EMD漂移修正
根据本文1.3节的分析,运用EMD分解方法对测点1的z方向基线漂移信号分解,根据RILLING等[15]的收敛条件,共提取15个IMF和一个趋势项,如图13所示。

图13 冲击振动信号EMD分解后的所有IMFFig.13 EMD decomposition of a impact vibration signal
去除趋势项和低频IMF可以有效的消除基线漂移,然而如何选择低频IMF的范围成为新问题,本文提出一种自适应的选择方法,具体为:从消除趋势项开始,每消除一项IMF,计算重构冲击信号的正负冲击响应谱,比较正负谱线的互相关系数,最大互相关系数所对应的重构信号为消除基线漂移的输出信号,整个过程如图14所示。

图14 正负相应谱最大互相关系数选择重构信号Fig.14 Reconstruct signal based on shock response spectrum correlation coefficients
图15(a)、(b)分别为去除趋势项、趋势项至第五个低频IMF冲击响应谱分析,对比图9原漂移信号及其冲击响应谱,可以看出重构信号的基线漂移得到了明显的改善,计算相应信号的最大响应谱低频斜率分别为-0.097 8、2.204;正负谱线互相关系数为0.418 9、 0.902 1。

图15 去除趋势项、趋势项至第五个低频IMF冲击响应谱分析Fig.15 Shock response spectrum analysis for trend item extraction and trend item to No.5 IMF extraction
根据上文的自适应方法,从去除趋势项开始,依次计算去除每一个IMF后重构信号冲击响应谱的低频斜率和正负谱互相关系数,如图16(a)、(b)所示,随着低频分量的去除,响应谱低频斜率趋于12附近,而互相关系数逐渐增加,在去除到第11个IMF时达到最大值0.998 500,其后的相关系数分别为0.997 820,0.996 890、0.994 196、0.990 139、0.990 059逐渐降低,这是因为重构信号高频分量有着趋向于高频噪音的趋势,响应谱趋于高频噪音的响应谱形式。图16(c)~(e)为相关系数最大值对应的输出重构信号、最大响应谱、正负响应谱,如图所示,重构信号消除了基线漂移保留了信号的高频成份。

图16 去除低频IMF后重构信号的响应谱分析Fig.16 Shock response spectrum analysis for reconstruct signal after low frequency IMF extraction
(4) 五点三次、小波、EMD漂移修正比较
根据上文的分析,五点三次、基于EMD的基线漂移修正算法均可以消除基线漂移,而小波修正算法部分消除了基线漂移,通过修正信号的正负冲击响应谱互相关系数比较,EMD算法的相关系数为0.998 400,五点三次算法的0.998 861,小波的相关系数为0.881 497,说明EMD算法的基线漂移修正效果基本和五点三次算法一致,强于小波修正方法,不同的是EMD算法在消除了低频漂移分量的同时对信号进行了分解,更有助于信号的分析及特征的提取。
3 结 论
冲击振动信号,受到传感器特性等因素的影响,冲击信号往往存在不同程度的基线漂移现象。本文提出通过计算冲击振动信号的冲击响应谱互相系数,开展信号漂移程度的量度及消除漂移成份效果评价的新方法。在本文开展的试验中,响应谱互相关系数较最大冲击响应谱的低频段斜率方法,更有效的对于基线漂移程度进行了定量描述;利用响应谱互相关系数,有效的选择EMD基线修正算法中去除本构函数的最优值,同时利用互相关系数比较了五点三算法、小波算法和EMD算法基线漂移的去除效果。试验数据证明,该方法可以有效的开展冲击信号基线漂移的程度判定和消除方法比较等相关工作。
[1] 赵小龙,马铁华,范锦彪. 高g值加速度计在高冲击下的失效特性的研究[J]. 传感技术学报,2012,(12):1668-1672.
ZHAO Xiaolong, MA Tiehua, FAN Jinbiao. The study of failure characteristic of highgacceleration in high shock[J]. Journal of Transduction Technology,2012,(12):1668-1672.
[2] 张国伟,冯顺山,俞为民. 高冲击过载加速度传感器零漂分析[J]. 华北工学院学报, 2004(1): 64-67.
ZHANG Guowei, FENG Shunshan, YU Weimin.Analysis of zero drift of the acceleration sensor in high-impulsion and high overloading[J]. Journal of North China Institute of Technology, 2004(1): 64-67.
[3] 夏伟强,马铁华,范锦彪,等. 压电式加速度传感器在高冲击环境下的零漂分析[J]. 传感技术学报, 2007(7): 1522-1527.
XIA Weiqiang, MA Tiehua, FAN Jinbiao, et al.Analysis of zero drift of the piezoelectric acceleration sensor in high impact testing[J]. Journal of Transduction Technology, 2007(7): 1522-1527.
[4] 宋颖,杜彦良,孙宝臣. 压电传感技术在轮轨力实时监测中的应用探讨[J]. 振动与冲击, 2010,29(1): 228-232.
SONG Ying, DU Yanliang, SUN Baochen. Travel rate analysis for a non-harmonically vibrating conveyor[J].Journal of Vibration and Shock, 2010,29(1): 228-232.
[5] 陈建军,王树乐. 冲击加速度零漂的一种改进小波修正方法[J]. 水雷战与舰船防护, 2012(4):18-23.
CHEN Jianjun, WANG Shule. An improved wavelet correction for zero shifted accelerometer data[J]. Mine Warfare & Ship Self-Defence, 2012(4):18-23.
[6] 袁宏杰,姜同敏. 实测爆炸分离冲击数据的分析和处理[J]. 固体火箭技术, 2006(1): 72-74.
YUAN Hongjie, JIANG Tongmin.Analysis and treatment of measured pyrotechnic shock data[J]. Solid Rocket Technology 2006(1): 72-74.
[7] EDWARDS T S. An improved wavelet correction for zero shifted accelerometer data[J]. Shock and Vibration, 2003, 10(3): 159-167.
[8] 胡灿阳,陈清军. 基于EMD和最小二乘法的基线飘移研究[J]. 振动与冲击, 2010, 29(3): 162-167.
HU Canyang, CHEN Qingjun.Research on baseline drift using least-square and EMD[J]. Journal of Vibration and Shock, 2010, 29(3): 162-167.
[9] WRIGHT C. Effective data validation methodology for pyrotechnic shock testing[J]. Journal of the IEST,2010,53(1): 9-30.
[10] PIERSOL A. Guidelines for dynamic data acquisition and analysis[J]. Journal of the IES, 1992,35(5): 21-26.
[11] 华师韩,田恒春. 冲击响应谱计算相关参数选择的研究[J]. 遥测遥控, 2005(6): 50-55.
HUA Shihan, TIAN Hengchun. Consideration of the parameters choice for shock response spectrum evaluation [J]. Telemetry and Telecontrol, 2005(6): 50-55.
[12] SMALLWOOD D O. Improved recursive formula for calculating shock response spectra[C]//Shock and Vibration Symposium. San Diego, CA, 1980.
[13] LALANNE C.‘Properties of shock response spectra’ in mechanical shock[M].Hoboken, NJ:John Wiley & Sons, Ltd, 2014:103-173.
[14] HUANG N E,SHEN Z,LONG S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society a—Mathematical Physical and Engineering Sciences, 1998, 454(1971): 903-995.
[15] RILLING G,FLANDRIN P,GONCALVES P. On empirical mode decomposition and its algorithms[C]. NSIP-03, Grado (Ⅰ),2003:8-11.
Baseline correction of impact signals using the cross-correlation coefficient of shock response spectrum
LI Haiguang1,2, PAN Hongxia1,REN Haifeng1
(1. College of Mechatronic Engineering, North University, Tai Yuan 030051, China;2 . Inner Mongolia Key Laboratory for Utilization of Bayan Obo Multi-Metallic Resources:Elected State Key Laboratory, Baotou 003310, China)
The baseline shift components in the impact vibration signals are associated with the high impact energy and sensor characteristics and they influence data analysis. This paper presented a new method for detecting the shifted baseline level and correction of the baseline shift. The proposed method was based on the cross-correlation coefficient between the positive shock response spectrum and the negative shock response spectrum. The new method for the baseline correction of impact vibration signal which represents the reconstruction of signal was realized by using the empirical mode decomposition(EMD) based on the cross-correlation coefficient. The validity and precision of the proposed method was demonstrated with analysis and validation of the signals generated in the operation process of an automation gun .
baseline shift; shock response spectrum; cross-correlation coefficient; empirical mode decomposition
国家自然科学基金资助项目(51175480)
2015-10-30修改稿收到日期:2016-02-17
李海广 男,博士生,副教授,1975年12月生
潘宏侠 男,教授,1950年10月生
TJ06
A
10.13465/j.cnki.jvs.2016.16.035
