双调和方程的有限积分方法
2016-09-15李书伟徐定华
李书伟,徐定华,余 跃
(浙江理工大学理学院,杭州 310018)
双调和方程的有限积分方法
李书伟,徐定华,余跃
(浙江理工大学理学院,杭州 310018)
利用有限积分法求解平面矩形区域双调和方程边值问题。首先,对双调和方程以及边界条件分别进行积分,得到一带有任意函数的线性常微分方程组;其次,将积分产生的任意函数分别进行插值估计,进而转化成为一可求解的线性代数方程组;最后,利用正则化方法求解奇异线性方程组,获得近似解误差估计。通过Matlab进行数值模拟实验获得数值结果,并进行误差分析。数值结果表明,与有限差分法、有限元法以及广义有限差分法相比较,有限积分法具有更高精度。
双调和方程;有限积分法;正则化方法;误差估计;数值解
0 引 言
双调和方程主要来源于流体力学和弹性力学,在工程技术方面应用极为广泛,相关理论和方法的研究一直是人们关注的热点,有限差分法[1-2]和有限元法[3]是常用的求解双调和方程的两种数值解法。有限差分法的优点是方法简单、计算量小,但是对边界区域规则性的要求非常高,难以处理复杂网格。有限元法虽然可以针对任何边界区域,但对于区域网格的划分有严格的要求。有限体积法[4]和边界元法[5]也是求解双调和方程非常重要的数值解法。有限体积法虽然自身包含几何信息、易处理复杂网格,但是计算比较复杂、不易提高精度。边界元法最大的优点是,可以使问题的空间维数降低,从而使计算工作量及其所需计算机容量大大减小,但是该方法需要求出问题的基本解,推导过程比较复杂。无网格法[6-8]是近年来新兴的一种数值方法,它是针对任何边界区域,并且只需在计算区域上选取若干节点及其径向基函数,不需要划分网格。
目前,偏微分方程边值问题的求解方法大多为有限差分法、有限元法、有限体积法和边界元法。迄今为止,对应用有限积分法求解偏微分方程的研究工作还不多,在该方法理论上的研究很少。本文研究了双调和方程边值问题的有限积分求解方法、数值算法、数值模拟以及该方法的收敛性分析,并通过模拟平面薄板受一均匀载荷时,研究静态平衡下薄板与载荷接触面上的位移分布与误差分析。本文针对研究双调和方程边值问题的求解方法,拟采用Wen等[9]提出的有限积分法对该问题进行数值求解,考虑了该方法的理论基础——积分的离散与函数的插值表示,结合文献[9]给出的利用有限积分法求解一维偏微分方程边值问题的解题思路,以求出双调和方程的数值解,并从理论上对该方法的收敛性做了分析。
1 预备知识
1.1积分离散形式
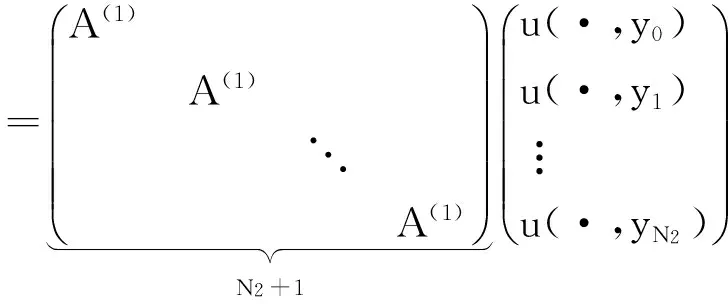
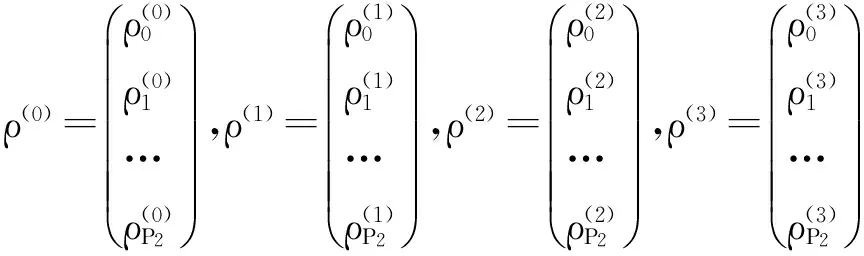
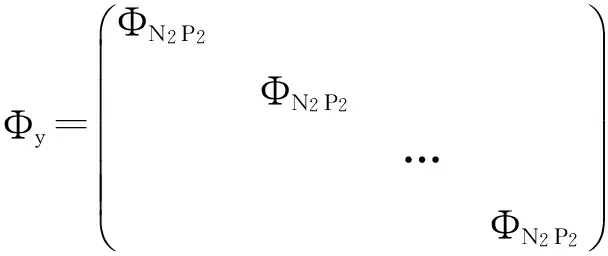
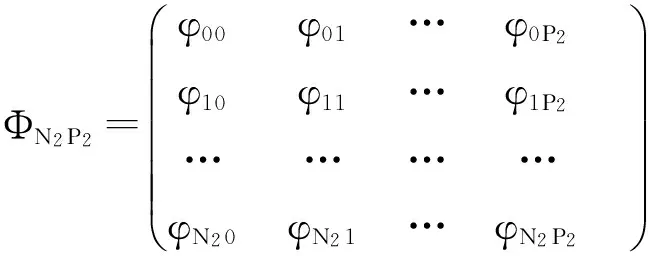
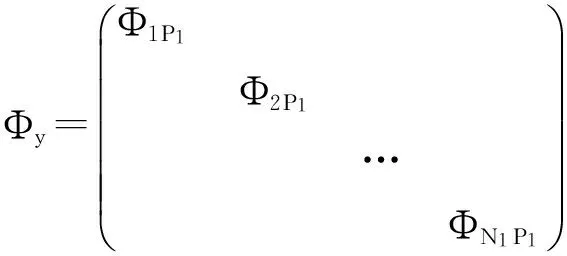
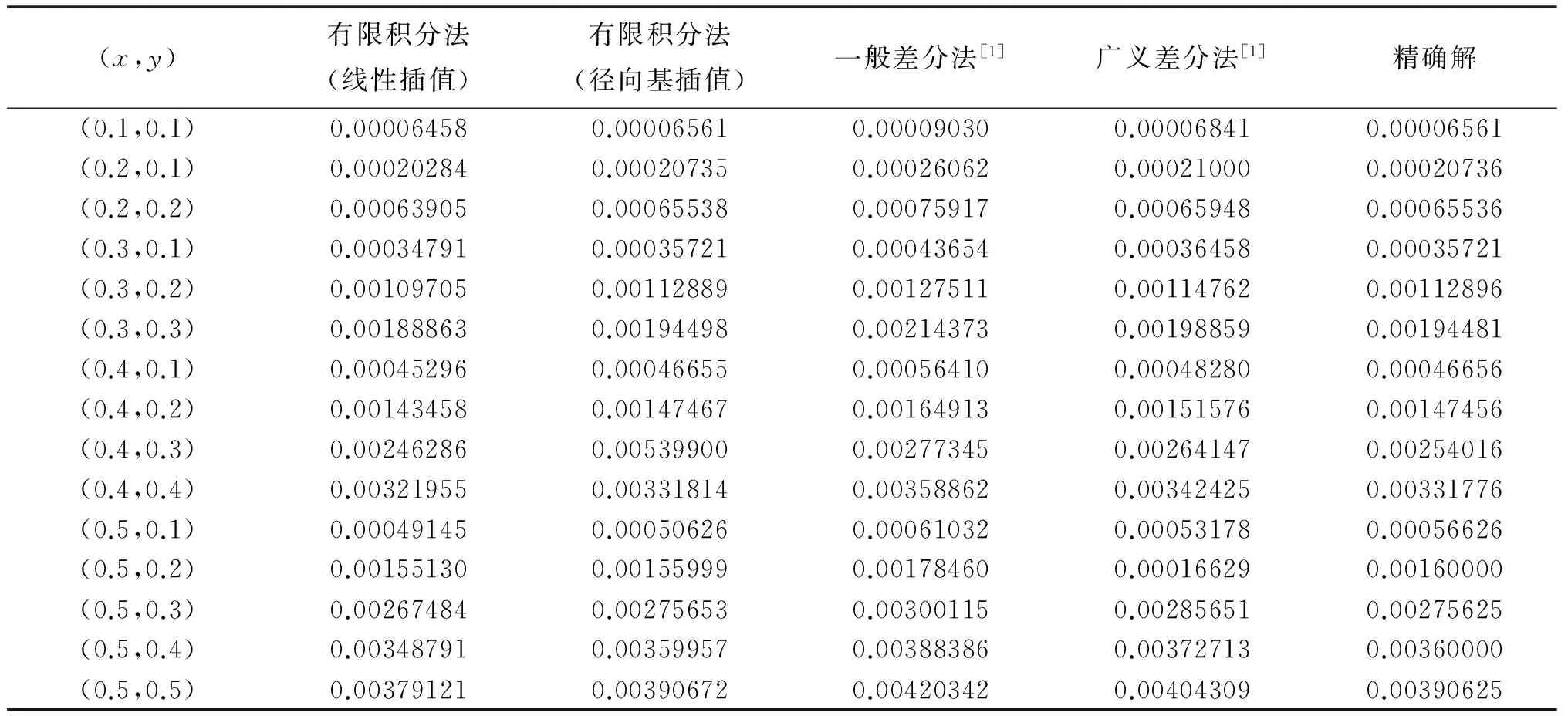
下面考虑一维情形[9]。考虑定义在[a,b]上的函数u(x),定义域离散为a=x0 (1) 则一次积分可离散为: k=0,1,…,N (2) 式(2)用矩阵表示为: U(1)=A(1)u (3) 其中: u=[u0,u1,…,uN]T. 同理,二次积分的离散形式为: U(2)=A(2)u=(A(1))2u. 更一般地,m次积分的离散结果为: U(m)=A(m)u=(A(1))mu. a=x0 c=y0 为方便表述,把网格节点标记为: (x0,ys),(x1,ys),…,(xN1,ys),s=0,1,…,N2, 称这样的顺序为标准顺序。 记Ux(x,y)和Uy(x,y)分别为对x和y的积分,则: s=0,1,2,…,N2, 用矩阵表示为: 具体可写为: 或简记为: 其中A(1)是由方程(3)求得的(N1+1)×(N1+1)维积分矩阵。 关于x的m次积分的离散形式为: 同理,关于y的积分的离散形式为: 为了将其转化为标准顺序,可进行一个初等行交换,其对应初等矩阵T=(Tmn),满足: 其中:i=0,1,…,N1;j=0,1,…,N2 1.2函数的插值表示 下面考虑线性插值[9]。对于1.1节给出的函数u(x)进行线性插值,即使用梯形规则,得: (4) 则: 用矩阵表示为: U(1)=A(1)u. 对于二阶线性插值有: U(2)=A(2)u=(A(1))2u. 对于m阶线性插值有: U(m)=A(m)u=(A(1))mu. =R(x)α+P(x)β (5) 其中:Ri(x)是径向基函数,αi是Ri(x)的系数,Pj(x)是多项式基函数,βj是Pj(x)的系数,径向插值的一个附加条件为: (6) 联立方程(5)和(6)得: (7) 则方程(7)的一阶积分插值为: 因此,其一阶的有限积分矩阵为: m阶积分的有限积分矩阵为: A(m)=Am. 考虑如下双调和方程边值问题: (8) 对式(8)中方程的x和y分别进行四次积分有: x2f1(y)+xf2(y)+f3(y)+y3g0(x)+ y2g1(x)+yg2(x)+g3(x)= dξ4dξ3dξ2dξ1dη4dη3dη2dη1 (9) 根据有限积分,方程(9)可离散为: +X3Φyρ(0)+X2Φyρ(1)+XΦyρ(2)+Φyρ(3) +Y3ΦxΛ(0)+Y2ΦxΛ(1)+YΦxΛ(2)+ΦxΛ(3) (10) 则方程(10)可以根据边界条件确定唯一解,并且其导数边界条件可以表示为: (11) 考虑方程(10),令: 则得到如下线性方程组: 简记为 (12) (13) 为避免因系数矩阵K的奇异性而导致错误的数值解,采用正则化方法解方程组(13),并对有限积分法计算结果做出误差估计。 证明可参见文献[12]中定理3.1。 特别的,当δ→0时,则有如下误差估计: 这里‖·‖表示L2-范数。 对K进行奇异值分解得: 则,有正则解: 令Rα=(αI+KTK)-1KT,由文献[13]可知: 由此可得: 根据引理1得: 又因为: 则: 特别地,令δ→0且α=hμ-3/E(μ>3),则误差估计为: 本节用有限积分法求解一个双调和方程,其数值结果与用有限差分法和有限元方法得出的数值结果相比较,通过实例验证方法是否有效、适用。 算例1考虑定解问题(8),令: h(x,y)=8[3x2(1-x)2+3y2(1-y)2+(6x2-6x+1)(6y2-6y+1)],f(x,y)=g(x,y)=0,本文用有限积分法解该问题,并将计算得的数值结果与文献[1]中的十三点格式的有限差分法和广义有限差分法以及文献[3]中的有限元方法得出的数值结果进行对比。数值结果及精确解见表1,数值误差见表2。 表1 数值结果 表2 误差结果 由表1、表2易见该方法具有如下优点:该方法是一种边界型无网格法,具有不需要划分网格的优势;与其它数值解法相比较,该方法具有更高的计算精度;该方法的精度与节点数量的多少无关。因此有限积分法是处理双调和边值问题的一种有效数值解法。 算例2在弹性力学[14]里,对于一受一般载荷的平面薄板,由薄板的小挠度弯曲理论可得该薄板弹性曲面的微分方程为: Δ2u(x,y)=q/D,(x,y)∈Ω, 作为算例,本文考虑一受均匀载荷q=10 N的平面薄板,板边长度a=1 m,宽度b=1 m,厚度δ=0.01 m,弹性模量E=1.372×108Pa,泊松比μ= 0.15,取其边界条件为固支边界条件,即: u(x,y)=0,(x,y)∈Γ, 将计算所得的数值结果与纳维叶精确解[13]: 做比较,数值误差结果见表3。 表3 数值误差结果 由表3易见,对于薄板小挠度弯曲问题,有限积分法计算所得的数值解很好地接近纳维叶法计算所得的精确解,由此可见,有限积分法对于求解薄板小挠度弯曲问题是有效的数值算法。 本文利用有限积分法求解了平面矩形区域的双调和方程的边值问题,与其他方法相比,该方法优点是无需划分网格并且成功地避免了有限差分方法中的截断误差问题,其计算结果比其他数值解法具有更高的精度。 虽然本文研究的是矩形区域的线性经典方程边值问题,但是有限积分法同样适用于非规则区域的非线性分数阶方程边值问题。对于非规则区域问题,只需要按照区域范围对函数每个积分点的积分区间稍作调整便可求解;对于非线性方程边值问题,只需按照文中所示的计算过程,将其转化成非线性代数方程组,通过迭代解法便可求得数值解;对于分数阶方程边值问题,由文献[9]和文献[15]可知文中所述的有限积分方法同样适用,只是分数阶方程积分所得的代数方程组有所差异。 [1] 李永海. 解双调和方程的一种混合广义差分法[J]. 吉林大学自然科学学报, 1993(3): 19-30. [2] CHEN G, LI Z, LIN P. A fast finite difference method for biharmonic equations on irregular domains and its application to an incompressible Stokes flow[J]. Advances in Computational Mathematics, 2008, 29(2): 113-133. [3] WANG C M, WANG J P. An efficient numerical scheme for the biharmonic equation by weak Galerkin finite element methods on polygonal or polyhedral meshes[J]. Computers and Mathematics with Applications, 2014, 68: 2314-2330. [4]WANG T. A mixed finite volume element method based on rectangular mesh for biharmonic equations [J]. Journal of Computational and Applied Mathematics, 2004, 172: 117-130. [5] 温希重, 李荣华. 求解平面双调和方程边界元法的误差分析[J]. 高等学校计算数学学报, 1988, 4: 298-310. [6] LI M, JIANG T S, HON Y C. A meshless method based on RBFs method for nonhomogeneous backward heat conduction problem [J]. Engineering Analysis with Boundary Elements, 2010, 34: 785-792. [7] LI M, CHEN C S, HON Y C. A meshless method for solving nonhomogeneous Cauchy problems[J]. Engineering Analysis with Boundary Elements, 2011, 35: 499-506. [8] HON Y C, YANG Z. Meshless collocation method by Delta-shaped basis functions for default barrier model[J]. Engineering analysis with boundary elements, 2009, 33(7): 951-958. [9] WEN P H, HON Y C, LI M, et al. Finite integration method for partial differential equations[J]. Applied Mathematical Modelling, 2013, 37(24): 10092-10106. [10] DUAN Y, ZHENG Y M, CENG P P. Convergence estimate of the RBF-based meshless method for initial-boundary value problem of wave equations[J]. Engineering Analysis with Boundary Elements, 2012, 36(3): 303-309. [11] HACKBUSCH W. Elliptic Differential Equations:Theory and Numerical Treatment[M]. Verlag Berlin Heidelberg: Springer, 1992: 103-109. [12] NARCOWICH F J. Recent developments in error estimates for scattered-data interpolation via radial basis functions [J]. Numerical Algorithms, 2005, 39(1/3): 307-315. [13] 刘继军, 不适定问题的正则化方法及应用[M]. 北京:科学出版社, 2005: 46-55. [14] 徐芝纶. 弹性力学: 下册[M]. 四版, 北京:高等教育出版社, 2006: 1-41. [15] HEYDARI M H, HOOSHMANDASL M R, MAALEK GHAINI F M. An efficient computational method for solving fractional biharmonic equation[J]. Computers and Mathematics with Applications, 2014, 68(3) :269-287. (责任编辑: 康锋) Finite Integration Method for Biharmonic Equations LIShuwei,XUDinghua,YUYue (School of Science, Zhejiang Sci-Tech University, Hangzhou 310018,China) In this paper, a finite integration method is applied to deal with boundary value problem of biharmonic equations on rectangle domains. Firstly, biharmonic equation and boundary conditions are integrated to gain a system of linear ordinary differential equations equipped with some arbitrary functions. Secondly, interpolation estimation is conducted for arbitrary function generated from integration. The boundary value problem is thus transformed to the system of linear algebraic equations which can be solved. Finally, regularization method is used to solve singular system of linear equations and to gain the error estimate of approximate solution. Numerical simulation experiment is carried out by Matlab software, and error analysis is conducted. Compared with finite difference method, finite element method and generalized finite difference, the results indicate that finite integration method presents higher precision. biharmonic equations; finite integration method; regularization method; error estimate; numerical solution 10.3969/j.issn.1673-3851.2016.01.022 2015-04-17 国家自然科学基金项目(11071221,11471287) 李书伟(1989-),男,山东德州人,硕士研究生,主要从事反问题理论及应用研究。 徐定华,E-mail:dhxu6708@zstu.edu.cn O242.2, O241.8, O343.1 A 1673- 3851 (2016) 01- 0133- 07 引用页码: 010802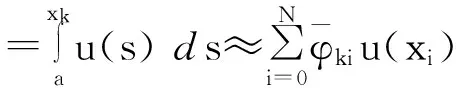
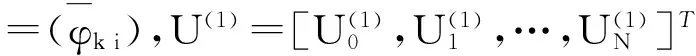


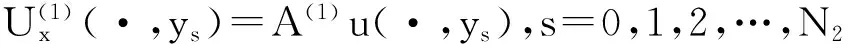
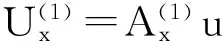
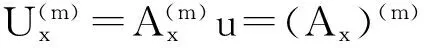
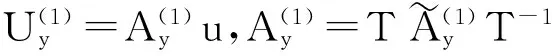
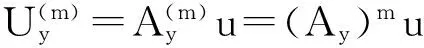

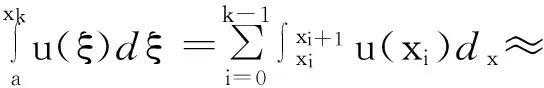
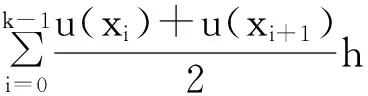
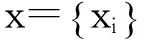
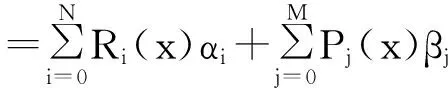
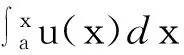
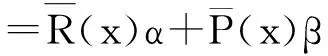
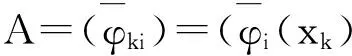
2 双调和方程的有限积分法
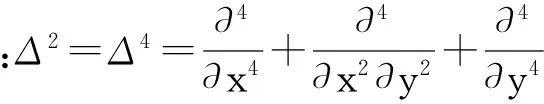
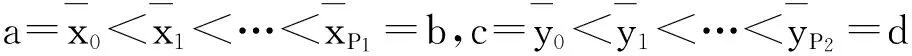
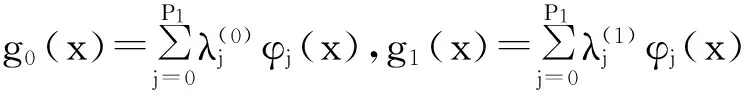
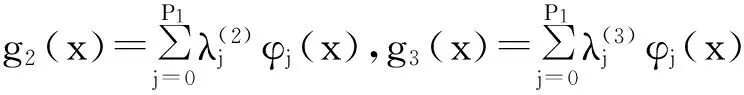

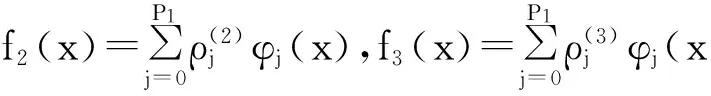

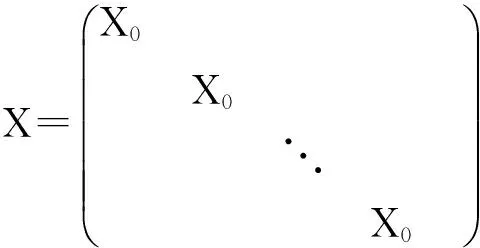

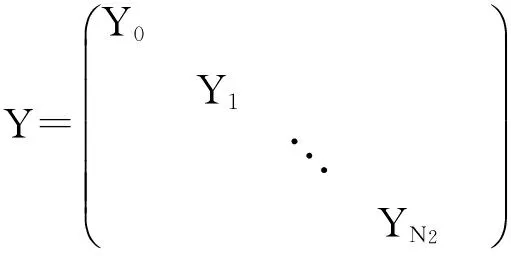
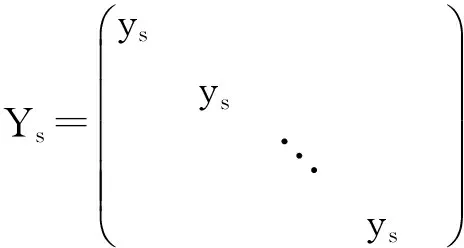
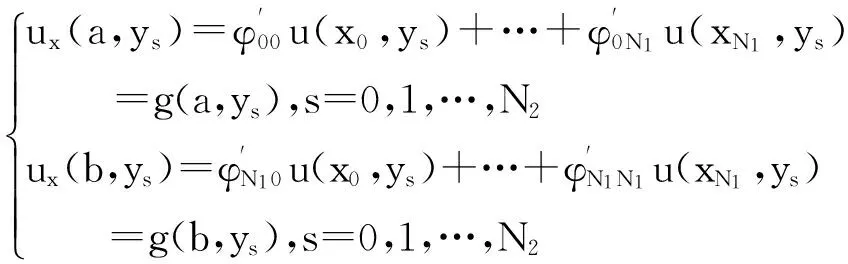
3 误差分析
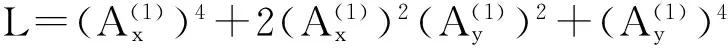
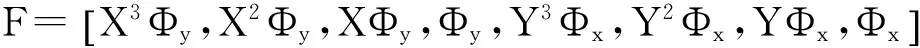
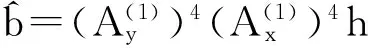
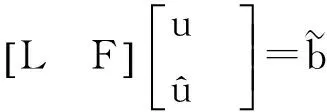

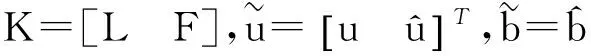
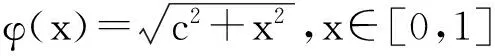
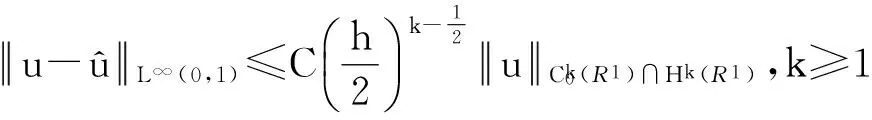
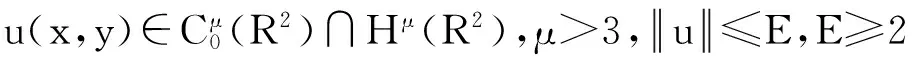
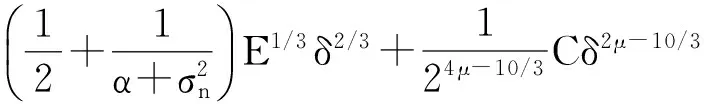
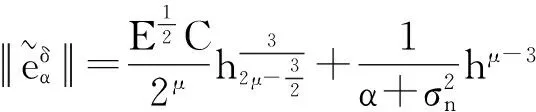
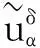
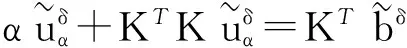
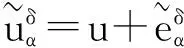
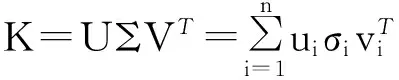
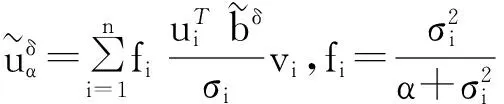
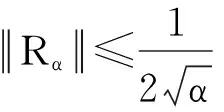
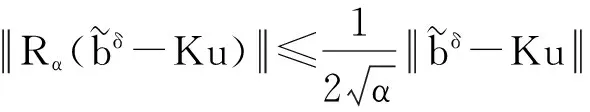
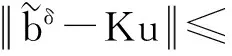
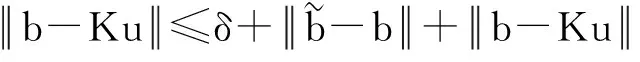
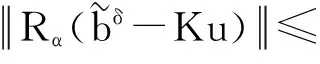
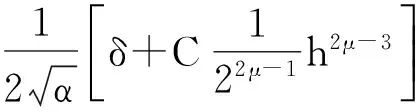
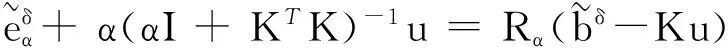

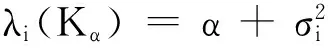
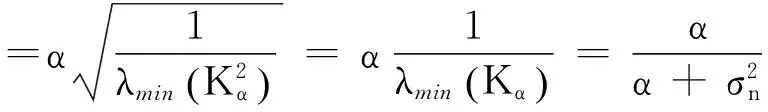
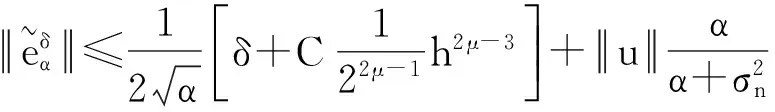
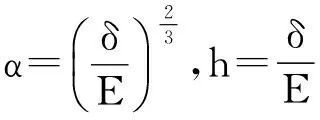
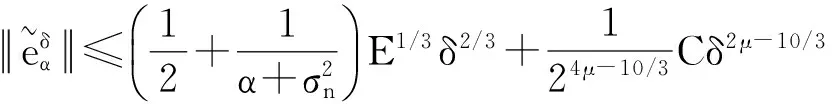
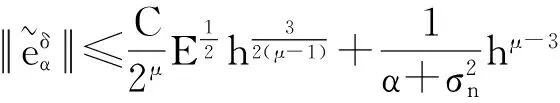
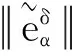
4 数值试验
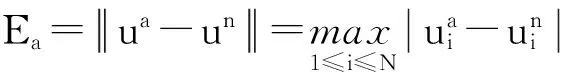

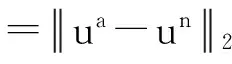
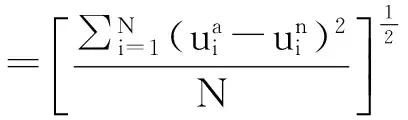

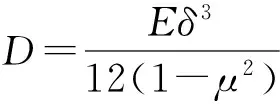
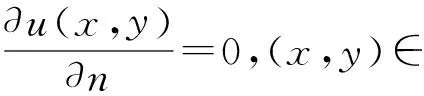

5 结 论
