电磁轴承单自由度简谐振动的自适应主动控制

徐　骏, 蒋科坚, 王　骏

(浙江理工大学信息学院， 杭州 310018)



电磁轴承单自由度简谐振动的自适应主动控制

徐骏, 蒋科坚, 王骏

(浙江理工大学信息学院， 杭州 310018)

为了防止电磁轴承转子的不平衡振动影响转子稳定的运行，需采取振动控制以减弱不平衡振动。转子不平衡振动可以分解为两个正交方向上的单自由度简谐振动，在两个正交方向上同时执行基于LMS算法的自适应振动控制，可实现转子径向二维的不平衡振动主动抑制。最后，在单自由度悬浮实验台上进行了振动抑制实验。实验表明所述方法振动抑制是有效的，并且能够在控制收敛范围内，对振动幅值和相位的变化实现自适应跟踪。同时，分析了步长因子、噪音、振动初相位等因素对其振动抑制性能的影响。

电磁轴承； 振动抑制； LMS算法； 自适应控制

0　引　言

转子的不平衡振动是一种同转子转速频率相同的单频率振动，是所有旋转机构最普遍的干扰激振源。尤其在转子高速转动情况下，由于这种振动力与转速的平方成正比，不平衡振动是影响转子高速稳定性的主要因素。作为目前唯一在工业中得到实际应用的转子振动主动控制元件——电磁轴承(也称为主动电磁轴承，active magnetic bearing)，不但可以控制电磁力把转子悬浮在期望位置，达到于传统机械轴承的转子支承效果，同时具有无接触、无摩擦、无发热、无需润滑等特点，在满足转子高速旋转要求的同时，还可以通过控制策略和参数的调节对转子施加可控电磁力，实现转子振动在线的、实时的、主动的抑制。

电磁轴承能通过控制，强迫转子按其几何轴旋转，达到振动抑制，提高旋转精度的目的，称之为不平衡补偿控制(unbalance compensation)。目前研究已经提出了多种采用电磁轴承进行转子不平衡补偿的方法。Schuhmann等[1]提出采用Kalman滤波器和最优状态反馈的方法控制不平衡力和减小转子振动。Huang等[2]基于Takagi-Sugeno模糊模型，实验研究了圆锥形电磁轴承的不平衡振动控制。Matras等[3]针对转子不平衡和由于叶片断裂引起的发动机转子大不平衡，这些振动往往频率已知，但幅值相位时变，提出自适应振动抑制方法。Arias等[4]为双盘柔性转子建立了有限元模型，每个单元视为欧拉梁结构，进行不平衡振动的计算和控制。Tamisier等[5]描述了采用电磁轴承的磨床电主轴的机械构造和控制系统结构，介绍了基于不平衡力激振识别的不平衡振动控制原理，但没有给出详细的算法。房建成等[6]建立了包含多振动源的转子动力学建模，并提出了刚性转子主动振动控制的要求。乔晓利等[7]提出了一种基于最小方差快捷分块的自适应滤波器振动控制方法，并设计了电磁轴承柔性转子多频率成分的主动振动控制。莫逆等[8]通过有限元法对转子进行建模，分析了再外力干扰下电磁轴承振动传递特性。高辉[9]提出了一种变步长的LMS自适应滤波器，用时变的补偿信号来消除反馈，完成了系统振动控制。Jiang等[10]分析了转子按几何轴旋转和按惯性轴旋转两种不平衡控制方法的实质区别和联系，并提出一种通过控制器接入点切换，方便实现转子按几何轴旋转和按惯性轴旋转两种不平衡控制方法。彭晓军[11]研究了自动平衡控制中通用陷波滤波器传递函数的参数与系统稳定性的关系，以此提出了新的陷波滤波器设计方法。孙岩桦等[12]提出了一种分散自适应控制算法，并验证了算法对系统参数的优化，给出了最优解的算法。

本文通过建模分析，把转子的径向不平衡振动分解为两个互相正交方向的独立振动，每个方向的振动都表现为与转速同频的单频率振动(简谐振动)。因此，本文提出一种基于LMS(最小均方误差)算法的单自由度振动自适应控制方法，可以在已知频率前提下，对单频率简谐振动实现有效抑制。并且，在振动变化时，能够对振动的幅值和相位实现自适应跟踪。在转子径向的两个正交方向上，同时执行这样的单自由度振动控制，可实现转子二维的不平衡振动抑制。在单自由度悬浮梁实验台上进行了振动控制实验，并分析步长、噪音等因素对其振动抑制性能的影响。

1　电磁轴承的工作原理

电磁轴承可以通过对电磁力的主动控制把转子悬浮在期望位置[13]，如图1所示。由两个位移传感器分别检测转子在X,Y两个互相正交方向的悬浮位置。每当转子在受到干扰偏离期望位置时，经由位移传感器检测出来转子的位置偏移量，经过控制器的控制策略产生相应的控制信号，然后由功率放大器放大产生驱动定子绕组的控制电流，定子绕组产生电磁力，使转子回到预期位置，这就是电磁轴承的动态稳定过程。通常，一个电磁轴承可以控制X,

Y两个方向的电磁力，一个转子由两个电磁轴承支承。因此，转子的径向悬浮需要4个方向的可控电磁力。最基本的悬浮控制方法，每个方向采用独立的反馈控制回路，可以实现电磁轴承-转子系统的悬浮控制，称为电磁轴承的分散控制。每个独立的反馈控制回路称为电磁轴承的单自由度的悬浮控制。以下讨论单自由度的电磁轴承悬浮控制模型。

图1　电磁轴承原理

2　电磁轴承单自由度悬浮建模和振动控制原理

单自由度的电磁轴承控制模型如图2所示。通过悬浮控制器C(s)产生悬浮控制信号，经过功率放大器P(s)和电磁轴承定子绕组A(s)后产生电磁力。电磁力和不平衡干扰力F(t)共同作用于转子，形成转子悬浮姿态变化。然后，把位移传感器检测到的转子位移信号y(t)实时反馈给悬浮控制器，以实现对转子的闭环反馈悬浮控制。

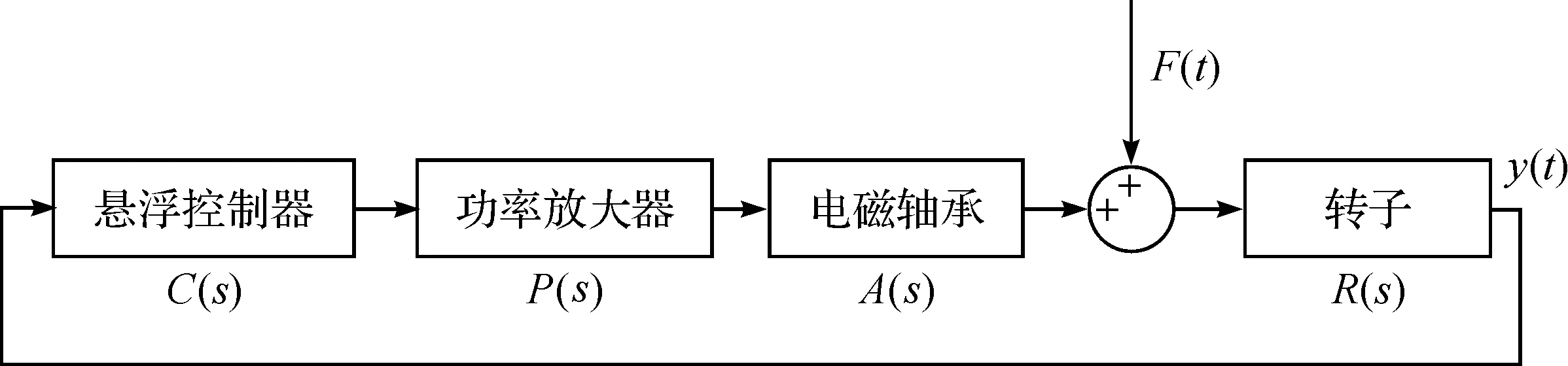
图2　单自由度电磁轴承控制模型

由于转子质量的不平衡，转子在转动时会产生与转速同频的单频率不平衡力，这种不平衡力大小与转速的平方成正比增加。从单自由度模型角度，转子的不平衡力可以看成是直接作用于转子的干扰外力。该干扰力始终与转速同频率，如图2中的F(t)，可用式(1)表示：

(1)

其中：e表示为转子的偏心距，m是转子质量，ω0为转子转速，θ为不平衡力的初相角。

根据模型等效原则，不平衡力F(t)等效成一个叠加在功率放大器P(s)输入端的不平衡干扰信号F′(t)，如图3所示。

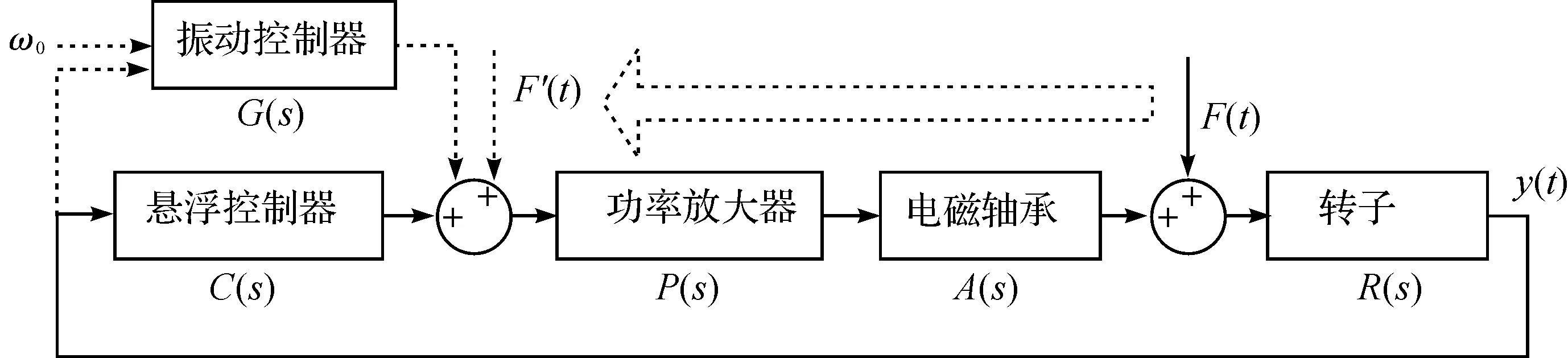
图3　单自由度电磁轴承振动控制等效模型

若功率放大器P(s)和电磁轴承A(s)的幅频特性P(jω)A(jω)=X(ω)φ(ω)，则不平衡干扰信号F′(t)可表示为：

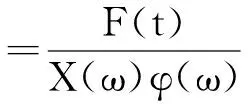
(2)

转子在不平衡力作用下，会产生转速同频的振动，即不平衡振动。在功率放大器前加入振动控制器(如图3)。振动控制器通过检测转速频率和当前的转子振动位移产生振动控制信号。振动控制信号也被叠加到功率放大器的输入端。在已知转子旋转频率下，振动控制器可产生幅值和相位可调的同步正弦信号，

ycontrol(t)=Asin(ω0t+φ)=αsinω0t+βcosω0t

(3)

其中:A为振动控制器信号幅值，φ是信号的初相角，[α,β]是振动控制信号的傅里叶系数。

如果这个振动控制信号ycontrol(t)与不平衡干扰信号F′(t)正好大小相等，相位相反，不平衡干扰信号就能被完全抵消，从而实现不平衡抑制的目的。在系统线性或局部近似线性条件下，转子的悬浮控制和不平衡振动控制是相互独立的，不相互影响。

振动控制器的控制可以归结为：根据转速频率，通过调节傅里叶系数[α,β]来改变正弦控制信号的幅值和相角。当控制信号改变时，转子振动也随之改变，直到振动控制信号与等效不平衡信号的幅值相位完全吻合，从而实现转子振动的主动控制。

3　自适应振动控制

振动控制器的内部结构如图4虚线框所示。振动控制器有一个输出，即振动控制信号ycontrol(t)；两个输入，一个为转速ω0，另一个为位移信号y(t)。实际中，转子悬浮位移y(t)是一个混有系统噪声的常数信号，另外，如果有不平衡振动，y(t)还会叠加不平衡振动信号成分。

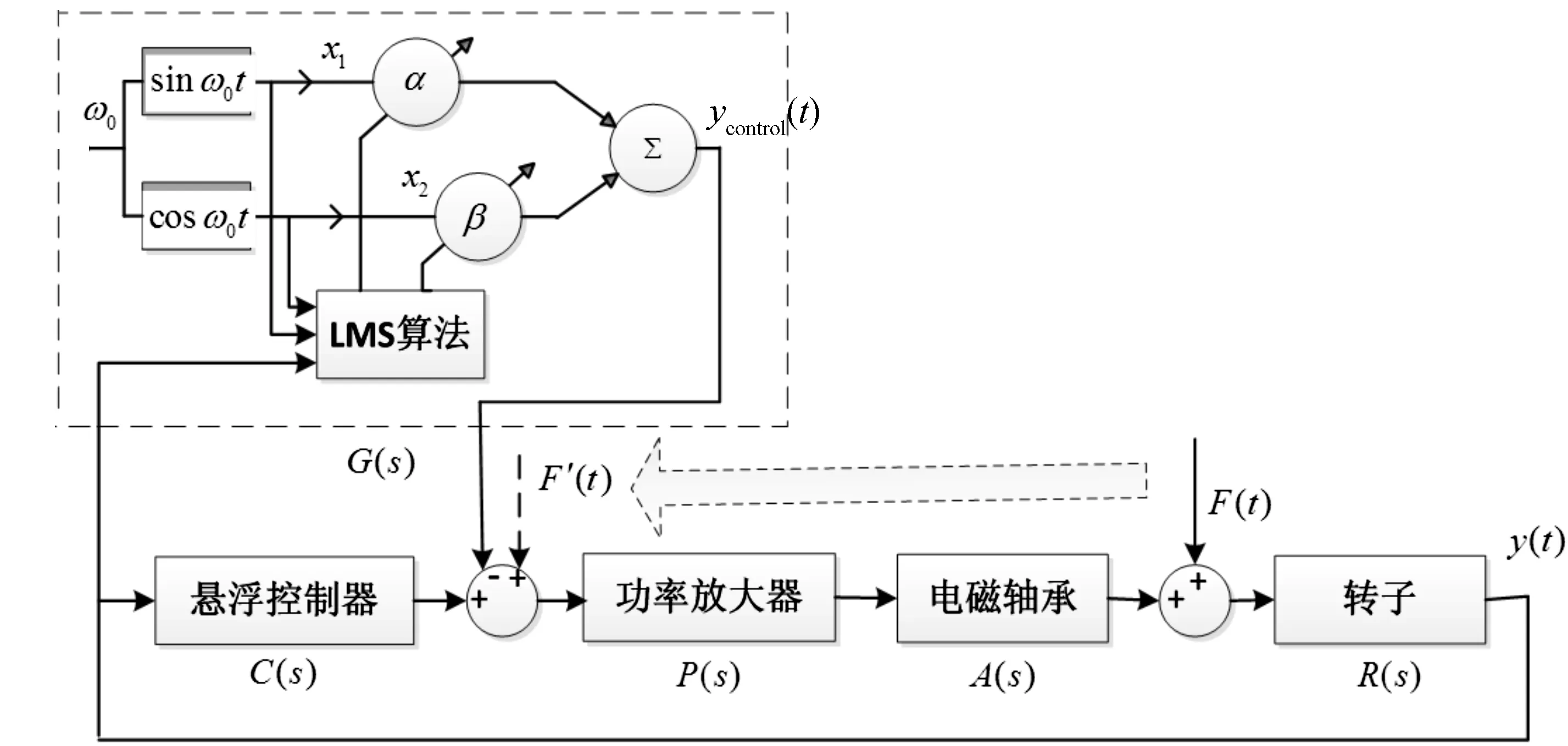
图4　单自由度电磁轴承振动控制原理

由如图4可知，如果不平衡振动信号F′(t)被控制信号ycontrol(t)完全抵消时，那么在位移信号y(t)中将检测不到不平衡振动成分，即控制误差为零。因此，控制的目的就是使控制误差ξ最小化，ξ可表示为:

ξ=F′(t)-ycontrol(t)

x1=sinω0t;x2=cosω0t;W=[α,β]

(4)

在实际应用中，为实现控制误差最小的目的，最广泛采用的控制目标函数是最小均方误差(MSE)。MSE具有唯一全局最小解，容易进行数学处理。MSE目标函数表示为：

MSE=E[ξ2]=E[|F′(t)-ycontrol(t)|2]

=E[F′(t)2]-2E[F′(t)WXT]+

E[WXXTWT]

=E[F′(t)2]-2E[F′(t)XT]W+

WE[XXT]WT

(6)

其中E[]表示信号的期望均值运算。

从式(6)可以看出，E[ξ2]是一个有关W的二次函数，其最小值可以通过对W求偏导为零时求得，

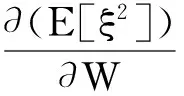
2E[F′(t)XT]=0

(7)

解得E[ξ2]最小时，最优的傅里叶系数矩阵W为:

WMSE=[α,β]=(E[XXT])-1E[F′(t)XT]

(8)

因此可知，存在一个最优傅里叶系数矩阵WMSE，当傅里叶系数矩阵W等于WMSE时，可以使控制误差达到最小均方误差，此时的控制信号能完全抵消不平衡振动信号F′(t)，即振动被完全抑制。

但是，由于实际中的F′(t)不知道，WMSE不能通过式(8)求解。为得到WMSE，本文设计了一个基于LMS(最小均方)的自适应算法，通过迭代的方法，来逐次逼近WMSE。迭代公式如下：

(9)

式(9)中，x1(k),x2(k),y(k)分别为x1,x2,y(t)的离散采样值。初始值[α(0),β(0)]可以取任意值，一般取[α(0),β(0)]=[0,0]；μ为步长因子，可调节算法的收敛快慢和稳定性。当μ较小时，迭代收敛较慢，但是控制精度较高；当μ较大时，控制收敛较快，但控制精度降低。μ需要取不同的值，以满足不同的振动频率下控制收敛的需求，并且μ也可能取负值，因为不平衡力作用于转子产生振动，力与振动的相位关系在某些频率段是反向的。在实际应用中，μ值通常事先测定，使用中按转子转速查表得到。

4　振动控制的实现机理和传递函数分析

从式(9)中可得，LMS算法的信号传递可用图5表示。

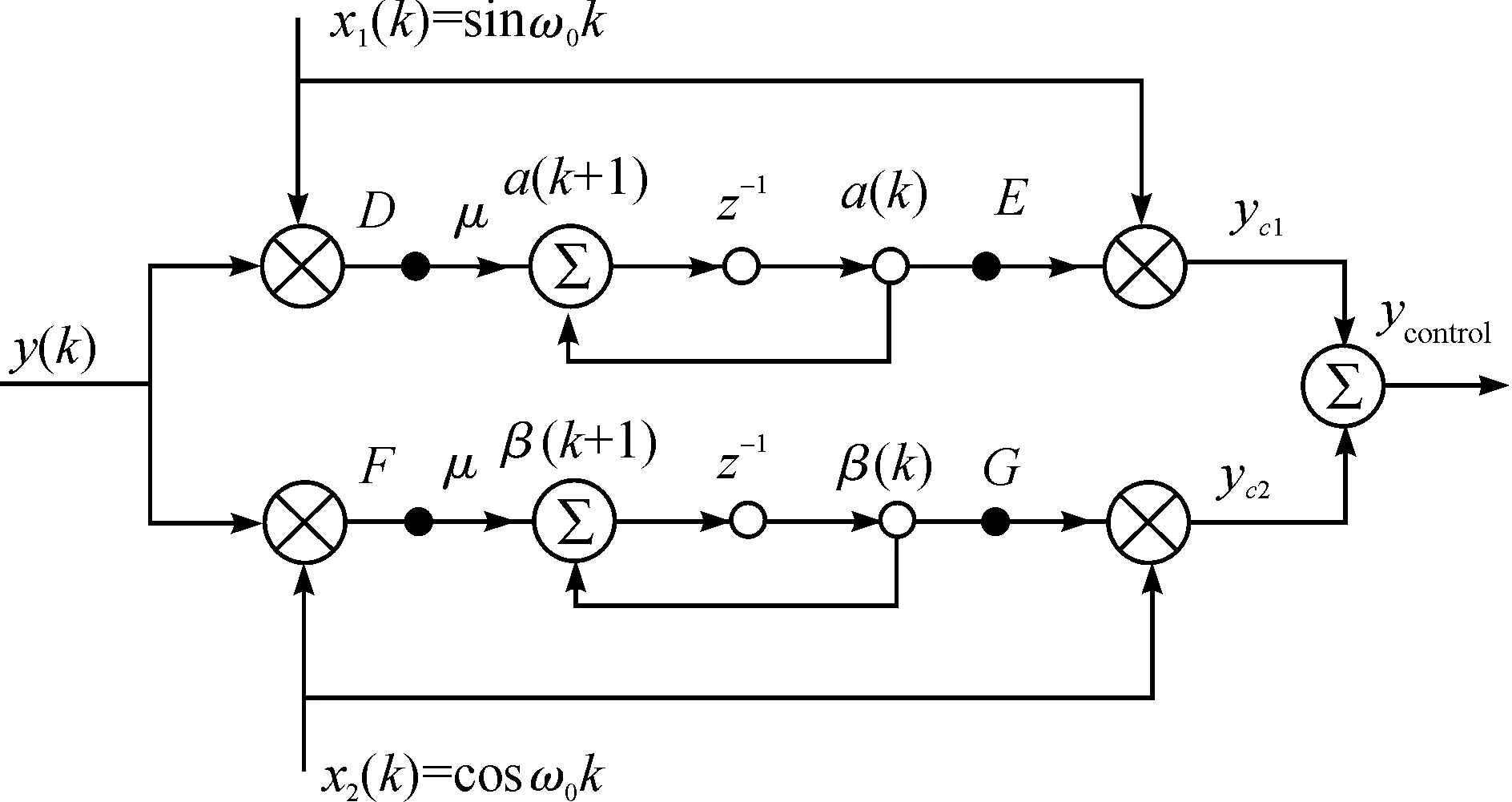
图5　LMS算法的信号传递

在k=n时刻y(k)输入为单位冲激响应δ(n-k)，则D点的信号为：

(10)

同时，D到E是传递函数为μ/(z-1)的数字积分器，其冲激响应为μu(n-1)，因此，E点的响应为:

μsinω0n,n≥k+1

(11)

如图5，再把x1(k)与其相乘，因此可以得到在yc1的输出函数为：

yc1=μsin(ω0k)sin(ω0n),n≥k+1

(12)

同理可得yc2的输出函数为：

yc2=μcos(ω0k)cos(ω0n),n≥k+1

(13)

所以，可以得到：

ycontrol=yc1+yc2=μsin(ω0k)sin(ω0n)+

μcos(ω0k)cos(ω0n)

=μu(n-k-1)cos((n-k)ω0)，

n≥k+1

(14)

因此，当k取0时，我们将其进行Z变换，即可得自适应振动控制模块的传递函数为

(15)

下面将从信号处理角度，分析采用如图4和式(9)的振动控制方法，其振动控制实现机理的实质。如图4可以简化成图6的控制模型，并表示为离散系统形式。同时，为了表述简化，把系统模块P(z),A(Z),R(z)看成一个整体模块B(z)。因为振动控制和悬浮控制是相互独立的，所以图6中省略悬浮控制模块，只讨论振动控制部分。

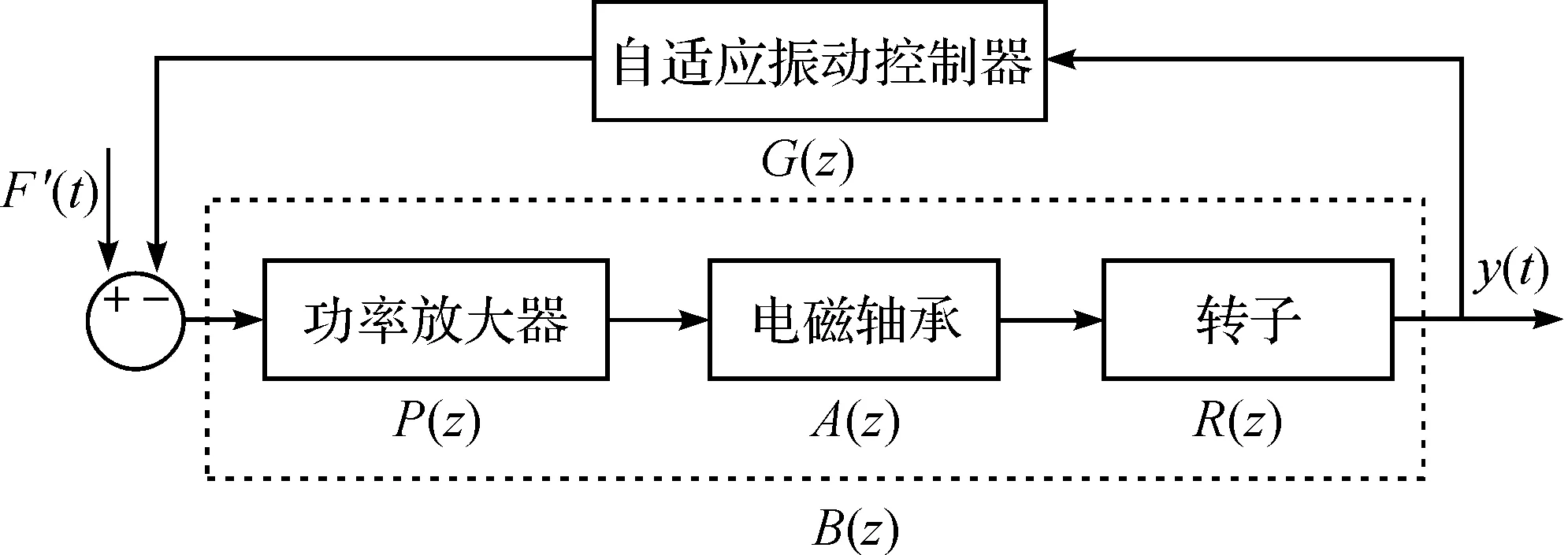
图6　电磁轴承自适应简化模型

从图6中，可以得到从F′(t)到y(t)的传递函数为

(16)

由于F′(t)是一个单频率的正弦信号，经过传递函数B(z)后，输出还是正弦信号，只是幅值和相位的变化。因此，对于单频率振动控制，B(z)可简化为Bz-m，其中B是幅值变化比，m是控制滞后。代入式(16)后得，

(17)

由于电磁轴承控制的实时性要求，控制滞后(100ms级)相比不平衡振动频率(6000r/min对应10ms)非常小。所以，对于频率较低的不平衡振动，可以忽略式(17)中的控制滞后因素。

忽略控制滞后，绘制式(17)的零极点位置和幅频特性如图7所示。

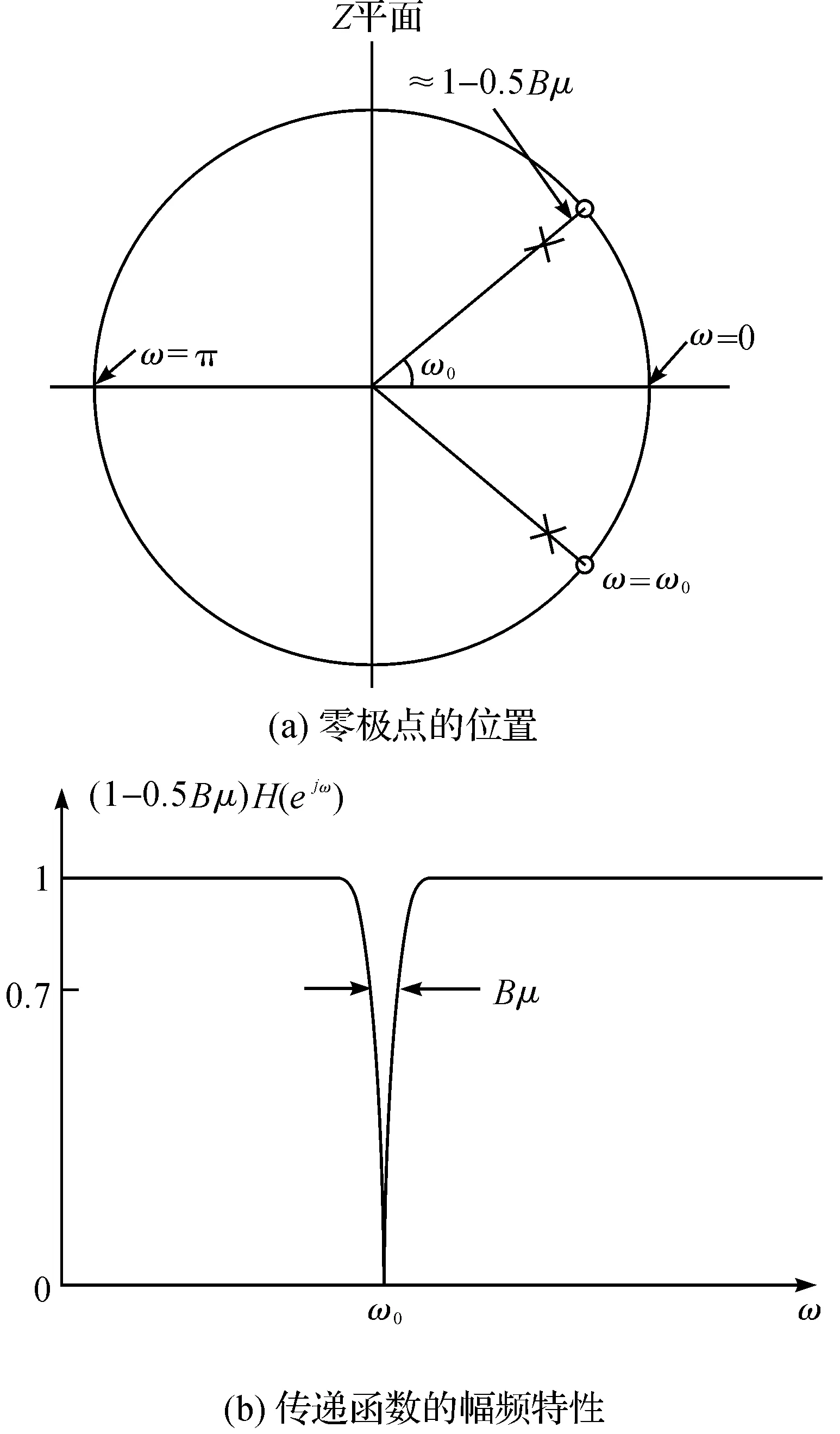
图7　振动控制系统的传递函数特性

传递函数的零点为：

z=e±jw0

(18)

可见在Z平面上，零点在单位圆上，相角为±ω0。因此该传递函数在频率为ω0时，其幅频特性值为0，即系统输入信号中频率为ω0的信号成分会被抑制到0。

传递函数的极点为：

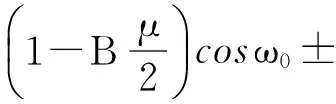
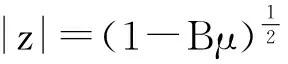
(19)

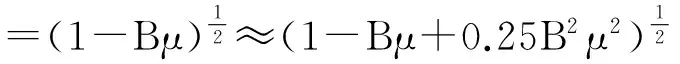
=(1-0.5Bμ);

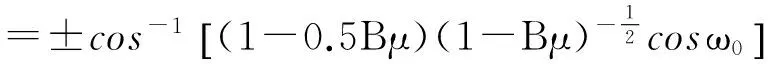
≈±cos-1[(1-0.5Bμ)(1-0.5Bμ)-1cosω0]

=ω0

(20)

由式(20)可知，当取Bμ≪1时，极点位置和零点几乎相同，所以在求其幅频特性时，零极点可以对消，使得在大部分频率，式(17)的幅频特性值为常数，只有在零点ω0处有一个凹口，即如图7(b)所示的形状。

同时，由式(20)可知，由于零极点之间的距离约为0.5Bμ。极点和零点的距离决定了凹口的尖锐程度。当所取的步长越小，凹口的尖锐程度就越尖，其阻带就越窄，对w0的信号的抑制更精确。反之，凹口就变得平坦，对w0信号成分的抑制精度下降。

5　实验与分析

5.1实验装置

实验装置单自由度电磁悬浮实验台如图8所示。实验台为悬浮梁结构，一端和铰链相连，另一端是由主动电磁悬浮支承。此实验台从力学角度模拟了电磁轴承的单自由度悬浮支承，数学模型完全相同。该实验台采用模拟线性霍尔位移传感器(霍尔芯片信号SS495)和PIC-1710采集卡对位移信号进行采集，控制算法调试采用Matlab的windows-realtime实时控制系统。主要参数如下：悬浮等效质量5.8kg；悬浮气隙0.88mm；电流刚度系数Ki=170.87N/A，位移刚度系数Kx=485424N/M，偏置电流1.25A。

通过实验发现，实验台悬浮结构的共振频率在23Hz附近。在共振频率，能以较小的激励获得较大的振动，振动信号清晰，有利于实验。当频率大于或小于偏离23Hz时，振动会逐步较小。因此，以下实验选择正弦激励信号频率为ω0=23Hz下进行。

图8　单自由度电磁轴承悬浮实验台

5.2振动抑制效果实验

实验在悬浮梁稳定悬浮的状态下进行。首先，在悬浮控制器输出信号中叠加23Hz的正弦干扰激励，悬浮梁在激励下振动。然后，启动振动控制，观察控制过程的振动变化情况。图9是悬浮梁的振动位移在初始阶段，加激励信号以及启动振动控制的整个时域过程。可以明确的看到在加入自适应振动控制后，正弦干扰振动逐渐减小。最后，振动被抑制到系统噪声相近的水平。实验结果表明，本文提出的振动控制方法是有效的。

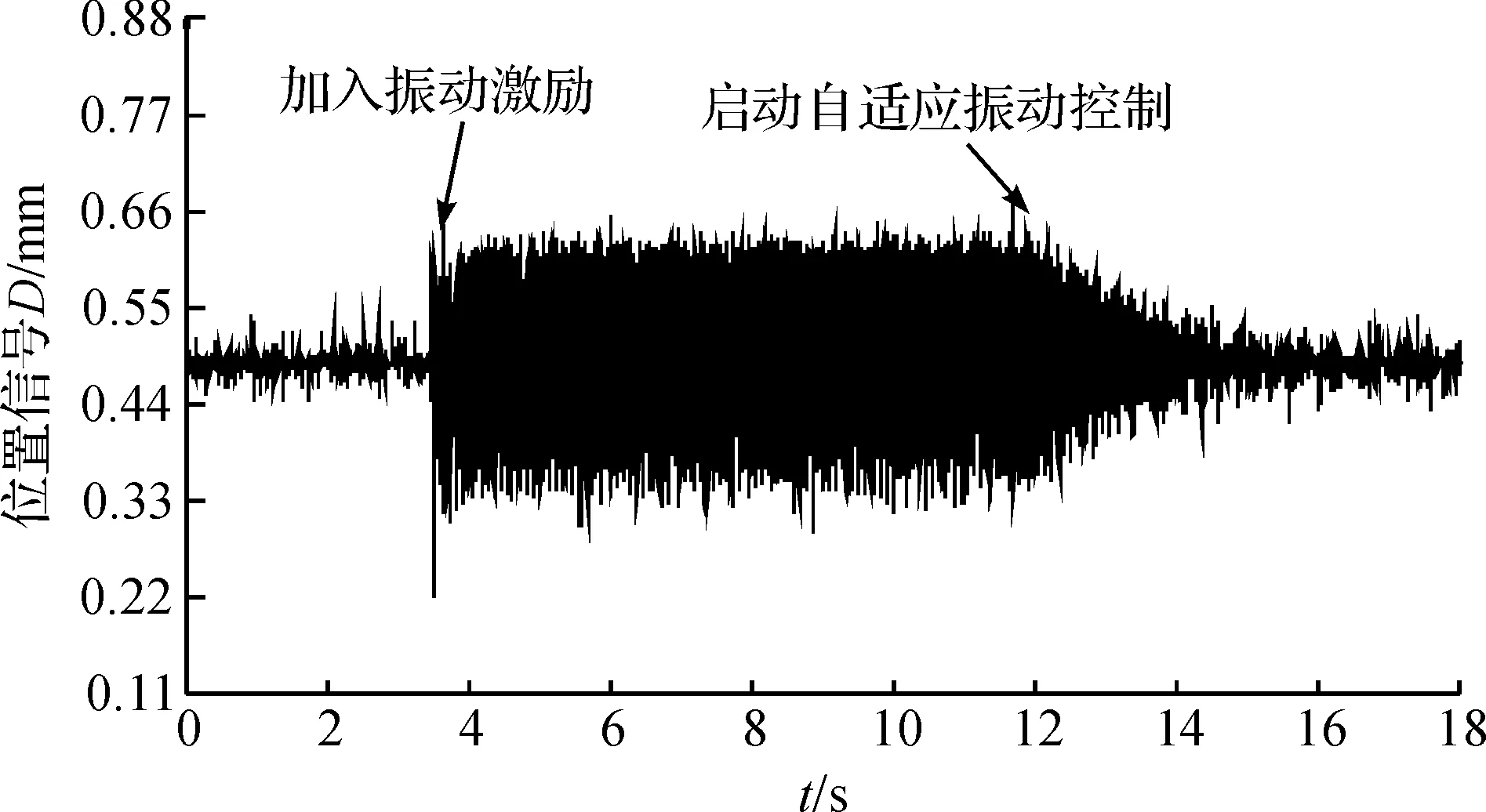
图9　下电磁轴水位置变化

5.3不同象限初相位的振动适应跟踪

本实验为了检验本文提出的振动控制方法对初相位在不同象限振动的自适应跟踪能力。实验采用了4组激励信号，频率和幅值相同，初相位分别在四个不同象限，其傅里叶系数分别[α,β]为[40,40] [-40,40], [-40,-40], [40,-40]，同时，初始的 [α0,β0]都是从[0,0]开始跟踪。

图10为实验结果，可见不论振动的初相位[α,β]位于那个象限，自适应振动控都可以实现准确的跟踪。因此，实验表明，对相位不断动态变化振动条件，本文提出的振动控制方法具有自适应跟踪能力。当然，必须在振动变化速度小于自适应控制的收敛速度的前提下。

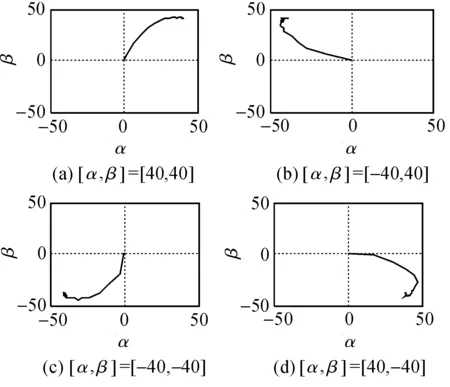
图10　不同象限[α,β]跟踪效果

5.4不同步长对自适应振动控制性能的影响

本实验为了测试当步长μ取值不同时，对自适应控制性能的影响。在振动控制能稳定收敛的范围内，分别取大小不同的4个μ值。实验结果如图11所示，在控制稳定收敛范围内，步长因子μ的增大可以显著加快振动控制的收敛过程。但是，步长因子μ的增大也使得控制稳定后，残余振动变大，即控制精度降低了。最后，当步长因子增加到0.0002，启动振动控制后，振动迅速增大，控制不能收敛，悬浮梁立即碰到上下两侧的悬浮极限位置了。因此，选取合适步长的标准是即保证振动控制能快速收敛，又能使残余振动在允许范围内。

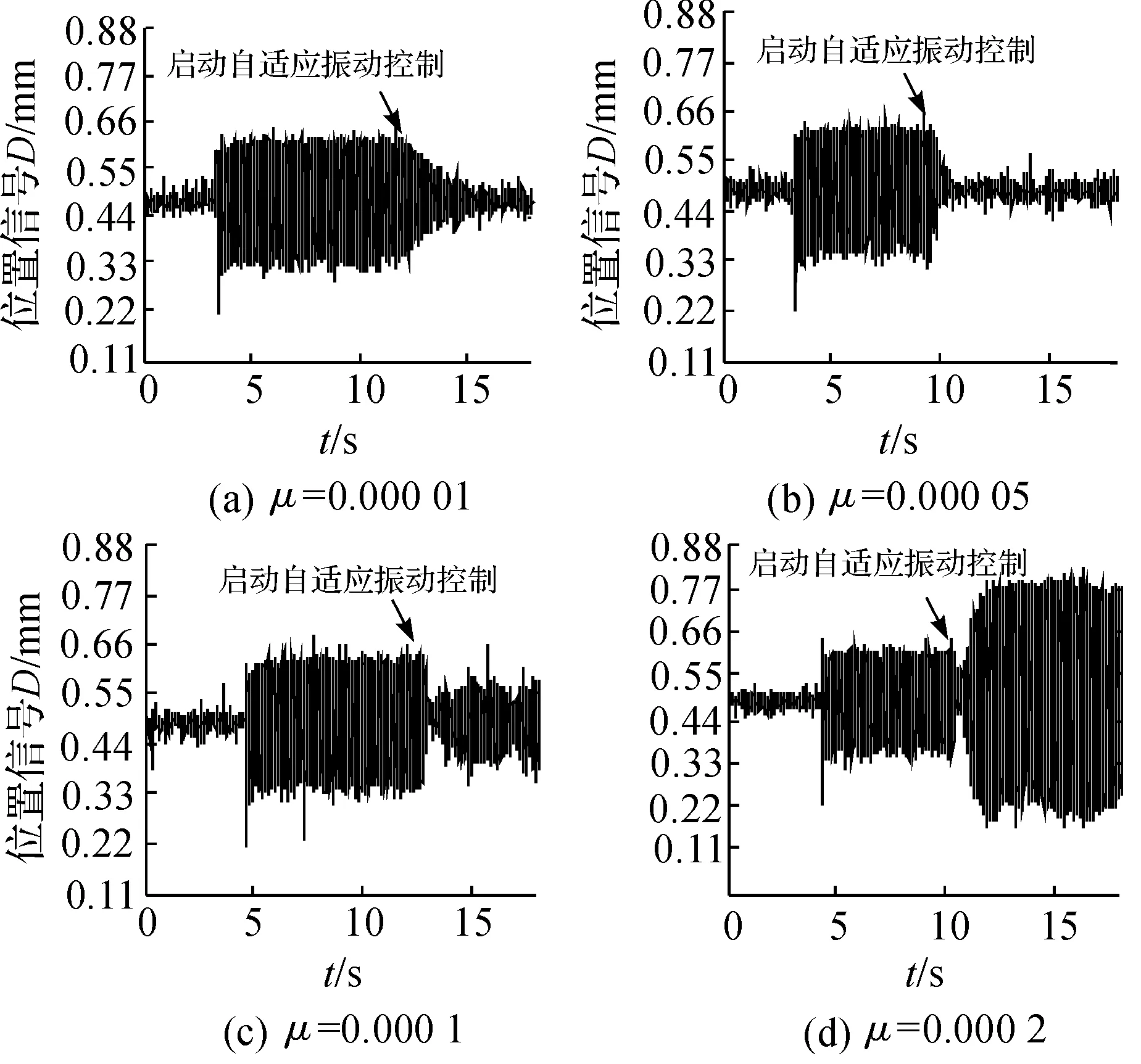
图11　不同步长自适应控制下悬浮位置变化

5.5不同噪声下的自适应振动控制效果

在实际中，由于系统噪声不可避免，所以实验将测试在存在噪音的情况下自适应振动控制器的性能。实验在系统中加入不同层度的随机噪声，噪声平均幅度分别为振动激励信号的20%，40%，60%，80%。

实验结果，在不同噪声条件下的振动控制时域过程如图12所示；对应自适应过程的控制信号[α,β]的变化轨迹如图13所示。可见，振动控制只对单频率的激励振动抑制有效，而对噪音引起的振动无效。噪声引起的振动在控制后依旧存在。同时，系统噪声的增大干扰了控制的收敛性能。图12和图13明显可见，随着系统噪声的增大，振动控制需要更多的步数才能到达稳定，而且收敛的路径更加曲折迂回。但总体而言，控制的抗噪声干扰能力还是不错的。在系统噪声加到80%时，超声振动幅度和激励振动几乎在同一水平，控制过程虽然振荡了一定时间，最终还是收敛到稳定状态。

图12　噪声不同时悬浮位置控制

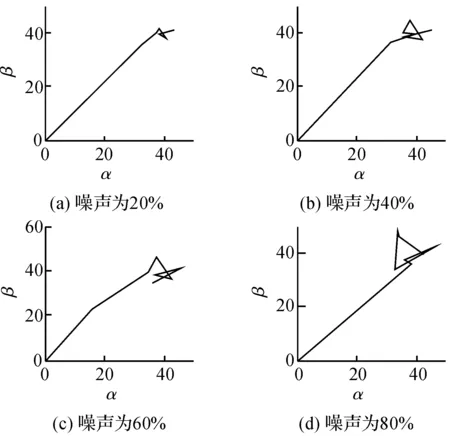
图13　噪声不同时傅里叶系数跟踪

6　结　论

本文提出一种基于LMS算法的单自由度振动自适应控制方法，可以在已知干扰振动频率前提下，对单频率简谐振动实现有效抑制，并且在振动变化时，能够对振动的幅值和相位实现自适应跟踪，对振动进行有效抑制。通过实验验证了该方法可以对单频率简谐振动起到很好的抑制效果，并分析了步长因子、噪音、振动初相位等因素对其振动抑制性能的影响。

对于转子系统，在两个正交方向上，同时执行这样的单自由度振动控制，可实现转子径向二维(两自由度)的不平衡振动抑制。

[1]SCHUHMANNT,HOFMANNW,WERNERR.Improvingoperationalperformanceofactivemagneticbearingsusingkalmanfilterandstatefeedbackcontrol[J].IEEETransIndElectron, 2012 ,59(2): 821-829.

[2]HUANGS,LINL.Fuzzydynamicoutputfeedbackcontrolwithadaptiverotorimbalancecompensationformagneticbearingsystems[J].IEEETransactionsonSystems,ManandCybernetics,2004, 34(4):1854-1864.

[3]MATRASA,GEORGET,ROBERTFetal.Suppressionofpersistentrotorvibrationsusingadaptivetechniques[J].JournalofVibrationandAcoustics,2006, 128(6):682-689.

[4]ARIASM,sILVAM.Finiteelementmodelingandunbalancecompensationforatwodisksasymmetricalrotorsystem[C]//Proceedingsof5thInternationalConferenceonElectricalEngineering,ComputingScienceandAutomaticControl.MexicoCity:IEEE, 2008:386-391

[5]TAMISIERV,FONTV,LACOUM,etal.Attenuationofvibrationsduetounbalanceofanactivemagneticbearingsmillingelectro-spindle[J].CIRPAnnals-ManufacturingTechnology, 2001, 50(1):255-258.

[6] 房建成,张会娟,刘虎. 磁悬浮刚性转子系统振动机理分析与动力学建模[J]. 控制理论与应用,2014(12):1707-1713.

[7] 乔晓利,祝长生. 永磁型电主轴多频率振动的主动控制[J]. 中国机械工程,2014(2):162-168.

[8] 莫逆,刘兴男,周燕,杨国军,等. 电磁轴承振动传递特性研究[J]. 振动与冲击,2015(6):79-83.

[9] 高辉. 主动磁悬浮轴承系统不平衡振动补偿研究[D].南京:南京航空航天大学,2011:20-25.

[10]JIANGKJ,ZHUCS.Auniformcontrolmethodforimbalancecompensationandautomationbalancinginactivemagneticbearing-rotorsystems[J].MeasurementandControl, 2012,134(3):1-13.

[11] 彭晓军. 磁电轴承中抑制不平衡振动的陷波滤波器设计方法[J]. 机械工程学报, 2006, 42(6): 120-123.

[12] 孙岩桦，罗岷，虞烈. 基于自适应陷波器的电磁轴承不平衡补偿方法[J]. 振动工程学报, 2000, 13(4):610-615.

[13] 方鹏,蒋科坚. 采用电磁轴承控制柔性转子临界转速分布的建模和仿真分析[J]. 浙江理工大学学报,2014(5):221-227.

[13] 虞烈. 可控磁悬浮转子系统[M].北京： 科学出版社， 2003: 48-55.

[14] 孙岩桦，虞烈，罗岷. 基于TMS320C30的电磁轴承不平衡补偿方案[J]. 电子技术应用，2001, 27(9): 33-35.

[15] 何振亚. 自适应信号处理[M]. 北京：科学出版社， 2002: 245-247.

[16] 刘彬，房建成，刘刚，等. 磁悬浮飞轮不平衡振动控制方法与试验研究[J]. 机械工程学报, 2010, 46(12):188-194.

(责任编辑： 陈和榜)

Adaptive Active Control of Single Freedom Simple Harmonic Vibration of Electromagnet Bearing

XUJun,JIANGKejian,WANGJun

(School of Information Science and Thechnology, Zhejiang Sci-Tech University, Hangzhou 310018)

To prevent imbalance of electromagnet bearing rotor from affecting stable operation of the rotor, vibration control must be taken to weaken unbalanced vibration. Unbalanced vibration of the rotor can be decomposed to single freedom simple harmonic vibration at two orthogonal directions. Simultaneous execution of adaptive vibration control based on LMS algorithm (least mean square error) at two orthogonal directions can achieve active inhibition of two-dimensional unbalanced vibration at radial direction. Finally, vibration suppression experiment was done on single freedom suspension experiment platform. The results show that the method mentioned is most effective, and can adaptively track the vibration amplitude and phase change while controlling the convergence range. Meanwhile, we analyze effects of the step size factor, noise, initial phase of vibration on vibration suppression porperty.

electromagnet bearing; vibration suppression; LMS algorithm; adaptive control

10.3969/j.issn.1673-3851.2016.01.011

2015-04-30

国家自然科学基金项目(11272288)；浙江省公益技术应用研究项目(2015C31063)；浙江理工大学研究生创新项目(YCX14022).计算机应用技术省重点学科研究生创新项目(XDY15005)

徐骏(1990-)，男，浙江杭州人，硕士研究生，主要从事功率放大器及磁悬浮控制方面的研究。

蒋科坚，E-mail: jkjofzju@163.com

TH133

A

1673- 3851 (2016) 01- 0064- 07 引用页码： 010503