单巷道双堆垛机作业路径优化问题研究

王小伟，张秋菊

（江南大学　机械工程学院，江苏 无锡　214122）

单巷道双堆垛机作业路径优化问题研究

王小伟，张秋菊

（江南大学机械工程学院，江苏 无锡214122）

针对不断提高的自动化仓库能效和输送作业效率要求，本文对长纵深巷道配两台堆垛机的作业形式进行了探讨。基于两个中心点车辆路由问题模式，建立了单巷道双堆垛机作业路径优化问题的数学模型。采用动态区域划分法将两个中心点车辆路由问题简化为一个中心点车辆路由问题，并设计了最大最小蚁群算法对两台堆垛机的作业路径进行优化。实例对比分析表明所建立的数学模型和给出的求解算法能够有效地求解双堆垛机作业路径优化问题，提高了自动化立体仓库的作业效率。

双堆垛机；路径优化；NP难题；蚁群算法；自动化立体仓库

自动化立体仓库是现代物流的发展趋势。典型的自动化立体仓库的巷道中通常配有一台堆垛机，当仓库巷道的纵深较长、且货物出入库比较频繁时，单台堆垛机往往难以满足物流输送需求。传统的做法是将巷道分段，每段巷道分别配一台堆垛机。由于每段巷道的货物输送频度不同，难免会存在堆垛机忙闲不均，货物输送效率的提高受到限制。针对上述问题，可以考虑采用一个巷道中配有两台堆垛机的形式，并通过合理调度最大限度地发挥堆垛机的输送能力，提高工作效率。

在同一巷道内配置两台堆垛机存在的最大问题是如何进行两台堆垛机的优化调度，避免干涉或碰撞。所谓的优化调度就是要根据一段时间内的一批入库和出库任务，合理地给两个堆垛机分配任务并安排任务执行顺序，要求这批任务的执行时间最短且两个堆垛机不发生干涉［1］。这属于典型的多车场车辆路由问题 （Multi-Depot Vehicle Routing Problem，MVRP）。对于这类问题的求解，目前大多采用启发式算法。例如在解决多AGV无碰撞规划问题上，贺丽娜和赵东雄均将Dijkstra算法和时间窗相结合，先顺序规划各个AGV的路径，通过检测后续规划路径是否与已存在的规划路径发生空间和时间冲突，并调用优化算法和规避策略进行最优路径的选择，从而实现 AGV的无碰撞路径规划［2-3］；马兆敏采用遗传算法和时间窗相结合实现了双钻头的孔群加工路径优化［4］；对于多配送中心的车辆调度问题，马宇红、殷脂分别采用几何重心分区方法和采用聚类分析最短距离分配法将多配送中心车辆调度问题转化为单配送中心车辆调度问题，大大降低了运算量［5-6］。文中利用区域划分和最大最小蚂蚁算法解决了双堆垛机的作业路径优化问题，使一个长巷道内两个堆垛机形式的应用具备可行性。

1　问题描述

1.1堆垛机的作业路径优化问题描述

如图1所示，图中为某物流配送中心自动化立体仓库巷道配备2个堆垛机的前视图。每过一段时间控制系统都会把这段时间内的所有入库任务和出库任务分配给巷道。堆垛机在两排货架的巷道之间行走。货架用于存放货物，货架两边都有出入库台。入库时堆垛机行走到入库台将货物搬运到货架上，出库时堆垛机将货架上的货物搬运到出库台上。堆垛机一次最多只能携带一个货物，两个堆垛机在同一轨道上行走但不能发生碰撞，要求2个堆垛机执行出入库任务的时间最短。

图1　巷道布局示意图Fig．1　The layout of the aisle

文中的堆垛机路径优化问题就是一种MVRP，问题中有2个车辆，2个中心，每个车辆的容量都为1，每个目标货位就是客户，他们的需求都为1。特别的是，车辆提供的资源是运输服务，有的客户想离开目标货位而有的客户想进入目标货位；车辆具有把客户从中心送到目标货位后又带其他客户离开目标货位的能力。

1.2双堆垛机出入库作业路径优化的数学模型

符号说明：

1）把一组出入库任务中目标出入库货位以及两组出入库平台O1、O2称为顶点v。所有顶点集合记为V=｛1，2，3…，n｝，vi（i=1，2，3，．．，n）∈V，vi水平方向编号为Xvi，垂直方向的编号为Yvi。

2）两个堆垛机m1、m2初始时刻分别位于顶点O1、O2，坐标为（Oxk，Oyk），k=1，2。堆垛机m1、m2的路径分别为R1、R2，包含的顶点个数分别是 n1、n2，n1+n2=n，R1∪R2=V。

3）E（i，j）表示顶点i与顶点j组成的边，如果路径Rk中存在任意相邻的顶点组成的边与E（i，j）∈Rk相同，则称，否则E（i，j）∉Rk；

假设：

1）堆垛机在水平方向和垂直方向的运动相互独立，运动速度恒定，分别是vx和vy。

2）单元货位间隔为常数，货位宽度为w，高度为h。

3）堆垛机从路径中一个顶点移动到下一个顶点的时间成本已知，不因顶点在路径的顺序不同而改变。

4）堆垛机启动、停止、货叉伸缩时间成本忽略不计。

堆垛机mk从目标顶点i运行到顶点j的时间成本根据i、j顶点类型不同而采用下面不同的计算规则［7］：

否则，

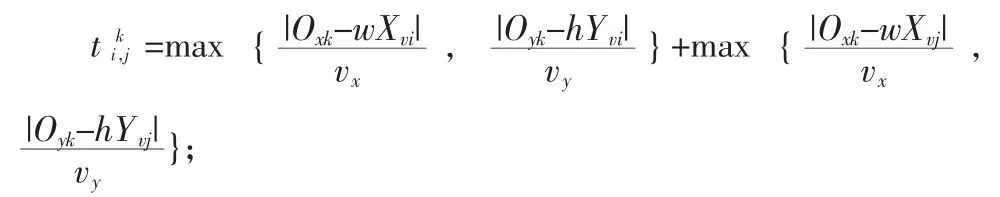
路径优化的目标是巷道式堆垛机的完成一组出入库任务的时间成本最小，它数学模型为：

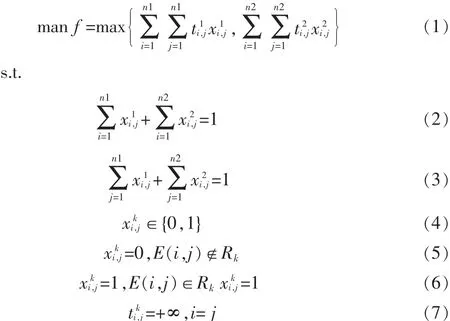
其中，目标式（1）确定目标函数是总路径的拣选时间最短。约束式（2）和（3）表示对每个顶点只被访堆垛机问一次；式（4）～（6）表明了决策变量xki，j的0-1属性以及xki，j的取值公式。（7）表示任意一个顶点到自身的时间按成本为无穷大，即顶点被堆垛机访问过后就不能再被访问了。

2　问题求解与算法设计

2.1动态区域划分

文中的两台堆垛机的作业路径优化问题属于多车场车辆路由问题（MVRP），解决车辆之间的冲突和碰撞是多车场车辆路由问题的关键。目前一般采用区域划分法、预测防碰撞等方法来解决车辆之间的冲突和碰撞。区域划分法顾名思义是通过几何中心分区、聚类分析等方法把工作环境划分为几个相互没有重叠部分的区域，而且每个区域只能容纳一辆车，从而实现防碰和冲突等问题；预测式避障则是首先为单个车辆分配好最优化的路径，然后根据每台车辆路径离线计算在运行过程中是否发生冲突，如果检测没有冲突则继续检测下一辆车，如果检测有冲突发生则立刻调整后车的路径来避免碰撞。虽然预测式碰撞通过合适的冲突检测和冲突消除方法，可以对系统做很好的优化，但是计算步骤较多，比较费时。区域划分法简单直接，计算速度快，更适合文中只有2辆车的MVRP。文中采用动态区域划分法，将出入库任务划分给不同的堆垛机，避免堆垛机之间的干涉与碰撞。划分步骤如下：

1）如图2，每隔一段时间（160 s），搜集这一段时间内所有出入库任务的目标货位。这里的时间间隔不是个定值，但是应当和优化后的执行时间尽可能接近，这样系统在执行的完成后就可以刚好收到优化后的命令。令两边出货台和入货台的中心点为配货中心，分别记为depot1、depot2。取index=1，记最小距离差为minD=+∞。

2）计算目标货位x坐标小于等于n的所有任务到depot1的距离总和，为sumOfDistance1；目标货位x坐标大于n的所有任务到depot2的距离总和，为sumOfDistance2；

3）如果 minD＞|sumOfDistance1-sumOfDistance2|，则minD=|sumOfDistance1-sumOfDistance2|。

4）index=index+1；

5）如果index小于货架列数就转到步骤②，否则将目标货位x坐标小于等于index的所有任务划分给堆垛机1，目标货位x坐标大于n的所有任务划分给堆垛机2。

图2　一批出入库任务的区域划分Fig．2　The zone division of a group of entry/exit storage task

通过任务区域划分，可将图2中的MVRP问题分解为2 个VRP问题，两个堆垛机互不干扰，不会发生碰撞。目前学者对于VRP问题的求解，大多采用Dijkstra算法［2］、遗传算法［8］、蚁群算法 s等启发式算法。蚁群优化算法 （Ant Colony Optimization，ACO）是由意大利学者Dorigo Marco等人提出一种模拟蚂蚁群体觅食行为方式的仿生优化算法。ACO的基本思想是：蚂蚁在某路口面临选择的时候，会随机选择一条路径，在通过这条路径时，它会释放一种化学物质，我们称之为信息素，释放信息素的浓度与路径长度相关。后来的蚂蚁再次来到相同的路口的时候，会根据前面蚂蚁留下的信息素来判断应该走哪条路径较短。蚂蚁数量足够多的情况下，它们就会形成一个有效的反馈机制，使整个蚁群最终找到那条通往食物最短的路径。实验证明蚁群算法在TSP问题上的设计及应用具有很强的发现较好解的能力。由于单纯的蚁群算法初期信息素匮乏，一般需要较长的搜索时间；后期易陷入局部最优，许多学者一直在对ACO做出改进，提出了很多ACO变种。其中较为优秀的当属MMAS最大最小蚂蚁系统算法，它对蚁群算法做了一下改进：

1）迭代结束后，只有最优解所属路径上的信息被更新，从而更好地利用了历史信息。

2）为了避免算法过早收敛于局部最优解，将各条路径的信息素限制于［τmin，τmax］，超出这个范围的值被强制设置为τmin或τmax，可以有效地避免某条路径上的信息素远大或小于其余路径，所有的蚂蚁都集中到同一条路径上，算法因此过早收敛的问题［10］。

蚁群算法在解决路径优化问题上有收敛性快，鲁棒性强的特点，文中采用蚁群算法中较为优秀的最大最小蚁群算法结合上述的区域划分法来实现对双堆垛机出入库作业路径的优化。

2.2算法设计

1）节点分类

采用上述的区域划分法将两个堆垛机要遍历的节点集合V分为2个集合V1和V2。V1只能由堆垛机m1遍历；而V2只能由堆垛机m2遍历；

2）初始化参数

堆垛机m1的路径R1为｛O1｝，m1的路径R2为｛O2｝；每个边之间的信息素为1．0；负责优化m1、m2路径的蚁群均有m只蚂蚁；蚁群最大迭代步数为Iteration。能见度因子为α、启发式因子β；信息素挥发率为ρ。

3）路径构造

每次迭代中m1的m只蚂蚁各自先随机选择一个入库顶点i，再根据贪心规则选择一个出库顶点j，并把刚才选择的vi，vj添加到路径集合R1中，顶点集合V1中删去vi，vj。重复上述过程，直到蚂蚁遍历所有顶点。其中当蚂蚁完成复合循环时，即集合V中剩下的顶点没有相应的出入库顶点与之配对，蚂蚁随机选择其中的一个顶点添加到路径集合R1中，并从顶点集合V1中删去，直至集合V1为空，m1的m只蚂蚁构造路径完成。m2的m只蚂蚁构造路径的方法和m1的相同，此处不再叙述。

贪心规则：如果蚂蚁处于当前顶点i，选择出下一顶点j的概率为

式中τi，j表示顶点i，j之间的信息素浓度；ηi，j表示顶点i，j之间的启发值，是成本ti，j倒数；参数α、β为常数，分别体现了信息素浓度和启发值的相对重要性［11］。

蚂蚁一般按贪心规则选择下一个顶点，即概率最大的顶点。但是如果总是是贪心规则，每次迭代时蚂蚁们的路径都是一样的。所以蚂蚁应随机采用贪心规则和轮盘赌规则选择下一顶点，即从［0，1］中选择一个随机数rand，如果rand＞0．8蚂蚁使用贪心规则选择概率最大的顶点；否则使用轮盘赌规则：从［0，1］中选择一个随机数r，从剩余顶点集合中计算累加选择概率sum——蚂蚁选择的第一个顶点概率为p1，则sum=p1，如果sum≥r，蚂蚁选择第一个顶点，否则sum加上选择第二个顶点的概率p2，如果sum≥r，蚂蚁选择第二个顶点，否则sum加上选择下一个顶点的概率pk，直到sum≥r，蚂蚁选择第k个顶点。这个选择规则被称为轮盘赌规则。

4）更新信息素

更新信息素包括边E（i，j）信息素挥发和蚂蚁在边E（i，j）释放信息素。

信息素挥发：τi，j=（1-ρ）τi，j

3　案例分析

以某一包装容器的自动立体仓库为例，此仓库的单排货架有3层，32列，层高1 200 mm，列宽650 mm。堆垛机巷道方向行走速度设为0．8 m/s，竖直方向升降速度为0．2 m/s。货架编码及出入库平台分布如图3所示。

图3　货架编码及布局Fig．3　The coding and layout of the rack

其中2个出入库平台均距离货架1个列宽，高0．5个层高。现有一组出/入库作业任务：

出库任务目标货位：1、6、9、11、16、29、35、36、52、60、64、70、88

入库任务目标货位：2、7、14、21、28、34、42、48、67、72、 76、89、94

要求对仓库该组出入库任务进行优化。

首先进行区域划分。经过计算后区域集合V1中的元素为：1、2、6、7、9、11、34、34、36、42、67、70、72、76；V2中的元素为：14、16、21、28、29、48、52、60、64、88、89、94。

表1　同一批出入库任务不同处理方法的路径及执行时间比较Tab.1　The comparison of path and its time cost handled with different methods

其次进行路径优化。MMAS算法参数：α=1，β=2，ρ=0．2，蚂蚁25只，迭代500次，得到优化后的路径见表1方式三所示，其中D0、D1分别代表出入库平台1、出入库平台2。

为便于对比，表1还给出了另外两种方式的路径及总作业时间：方式一不做优化，两个堆垛机根据任务到达次序依次执行；方式二，不采用双堆垛机的形式，而是将巷道均分为两个巷道各配一台堆垛机。两种方式的处理结果见表。从表1可见：经过本文中算法优化后堆垛机作业执行时间明显减少。

4　结　论

本文对单巷道双堆垛机形式的作业调度与路径规划优化算法进行了研究，通过动态区域划分与最大最小蚂蚁算法，有效地对一个巷道中有两个堆垛机的作业路径进行了优化。实例对比分析表明，仓库物流效率有明显的提高。当仓库巷道的纵深较长、且货物出入库比较频繁时采用一个巷道中配两台堆垛机的形式，不失为一种可行的、效率较高的作业方式。

［1］朱文真，唐敦兵．基于遗传禁忌搜索算法的自动化立体仓库出入库路径优化研究［J］．机械科学与技术，2011，30（7）: 1202-1206．

［2］贺丽娜，楼佩煌．基于时间窗的自动导引车无碰撞路径规划［J］．计算机集成制造系统，2010，16（12）:2630-2634．

［3］赵东雄．多自动导引小车系统 （AGVS）路径规划研究［D］．武汉：湖北工业大学，2014．

［4］马兆敏，戴青玲．基于双钻头的孔群加工路径优化算法［J］．机床与液压，2010，38（6）:13-15．

［5］马宇红．多车场多车型车辆调度问题及其遗传算法［J］．数学的实践与认识，2014，44（3）:107-114．

［6］殷脂．多配送中心物流配送车辆调度问题的分层算法模型［J］．系统管理学报，2014，23（4）:602-606．

［7］丁彩红．锂电池化成物流系统的立体仓库调度算法研究和建模［D］．上海:东华大学，2014．

［8］龚延成．基于遗传算法的物流配送车辆调度问题研究［J］．数学的实践与认识，2004，34（6）:93-97．

［9］张裕华．基于蚁群算法的应急物流配送车辆调度研究［J］．物流科技，2009，5（5）:47-50．

［10］陈昊．蚁群优化算法的原理及其应用［J］．湖北大学学报，2006，28（4）:350-353．

［11］Macro Dorigo，Thomas Stützle．Ant Colony Optimization［M］．London:A Bradford Book，2004．

［12］Thomas Stützle，Holger H．HoosMAX-MIN Ant System［J］．IEEE Computational Intelligence Magazine，2006，11（4）:28-39．

Job path optimization of single aisle with double stackers for automatic warehouse

WANG Xiao-wei，ZHANG Qiu-ju
（School of Mechanical Engineering，Jiangnan University，Wuxi 214122，China）

As the requirements for the energy efficiency of automated warehouse and delivery operation growing quickly，the form of two cranes worked in a long aisle are discussed in this paper．The problem is treated as double-depot vehicle problem and its mathematics model is built．Then the problem can be simplified as single-depot vehicle problem dynamic region partition．So the Max-Min Ant System（MMAS）algorithm is extended to the problem associated the path of Double Cranes in one aisle of an Automatic Storage and Retrieval System．Finally，the algorithm is performed with practical case，which produces high-quality for the problem．

double stackers；path optimization；NP-hard problem；ant colony optimization；automatic warehouse

TN01

A

1674－6236（2016）02-0068-04

2015-03-16稿件编号：201503210

王小伟（1989—），男，江苏灌南人，硕士研究生。研究方向：物流自动化。