h形抗滑桩内力变形机理数值分析研究

李立锋，王桂尧，张永杰，周欢

（长沙理工大学土木建筑学院，湖南长沙 410004）

h形抗滑桩内力变形机理数值分析研究

李立锋，王桂尧，张永杰，周欢

（长沙理工大学土木建筑学院，湖南长沙 410004）

运用数值分析软件，结合典型工程案例，分析h形抗滑桩在滑坡工程中的受力和变形特性，对比分析不同前后排桩间距、不同桩体锚固长度等因素对h形抗滑桩桩身内力与变形的影响规律。结果表明，桩体最大位移出现在桩顶，由于连续横梁的存在，前后排桩桩体协调变形；前后排桩最大弯矩均出现在滑面以下约2.5m处，最大剪力均出现在滑面附近；桩间距、锚固长度对基桩变形的影响程度大于内力，不同桩间距、不同锚固长度，桩体的最大弯矩变化不大；桩顶位移随着桩间距的变大而减小，当桩间距大于4b（b为桩体截面宽度）时，增大桩间距不会减小桩顶位移，前后排桩间距宜取2b～4b；随锚固长度的增加，桩顶水平位移达到一定值后保持不变，建议锚固长度取1/3～1/2桩长。

公路；h形抗滑桩；滑坡；桩顶位移；弯矩；剪力；桩间距；锚固长度

1　h形抗滑桩及其研究现状

h形抗滑桩支挡结构是通过在坡体内设置前后2排桩，中间用连续横梁连在一起，前排桩较短，后排桩较长，且后排桩具有悬臂桩段的框架结构。其结构形式见图1。

图1　h形抗滑桩支护结构示意图

与一般抗滑桩相比，h形抗滑桩应用于滑坡治理工程中，其较大的稳定性和侧向刚度可提高桩体抵抗侧向变形的能力；其桩体受力分布更合理，可有效减少桩身内力；可和锚杆、锚索及格构梁等支挡结构联合应用；可通过调节前后排桩中间的连续横梁高度，使后排桩具有不同的悬臂长度，既能优化和改善桩体结构受力分布，也能适应不同的地形、地质条件及施工环境。

对于h形抗滑桩内力和变形的研究，王羽采用三次超静定图乘法建立了h形抗滑桩受荷段内力计算方法与锚固段弹性桩计算方法；周金成利用有限元软件建立了h形抗滑桩的数值分析模型；赵海玲等采用ANSYS数值分析软件研究了其受力状态和前后排桩变形情况；马青力采用数值分析方法，结合工程实例对h形桩板墙桩土相互作用进行了分析；张泽坤采用有限元软件ANSYS对h形抗滑桩加固膨胀土边坡进行了数值分析研究；欧孝夺、孙涛、张永杰等通过试验、数值分析与现场试验探讨了h形抗滑桩在边（滑）坡工程中的承载变形特性。但现有研究方法对于桩周岩土体的作用力分布形式不统一，致使得出的桩体承载变形规律不明确，且对各因素对h形抗滑桩承载变形特性的影响规律与影响程度缺乏系统分析。

该文在现有研究的基础上，运用数值分析软件对实际工程案例进行数值模拟计算，分析h形抗滑桩的内力变形特征，并通过改变基桩设计参数获得不同设计参数对h形抗滑桩内力变形的影响规律。

2　h形抗滑桩数值模型的建立及计算方法

2.1数值模型

选用数值分析软件MIDASGTS（试用版）对贵州省三凯（三穗—凯里）高速公路王家寨滑坡实际工程进行数值模拟计算分析。该滑坡体沿路线长度为196.75m，上部为碎石土，呈松散～中密状，下部为强风化硅化绢云母板岩。滑坡后缘拉裂缝与道路中线的最大水平距离为192m，滑体平均厚度21.4 m，最厚达39.5m，平均宽85m，体积约51万m3，属于大型滑坡。采用预应力锚索+h形抗滑桩进行处治。h形桩的设计尺寸为：悬臂段长3.5m，前排桩长17～22m，后排桩长23.5～28.5m；前后排桩尺寸为3.0m×3.0m，横梁尺寸为3.0m×3.0m；前后排桩间距为6.5m，桩基列距为6m；桩体采用C30砼。悬臂端顶部布设2根1000kN预应力锚索。为便于数值模拟，对该工程进行简化（见图2、图3）。

图2　典型工程的模型简图

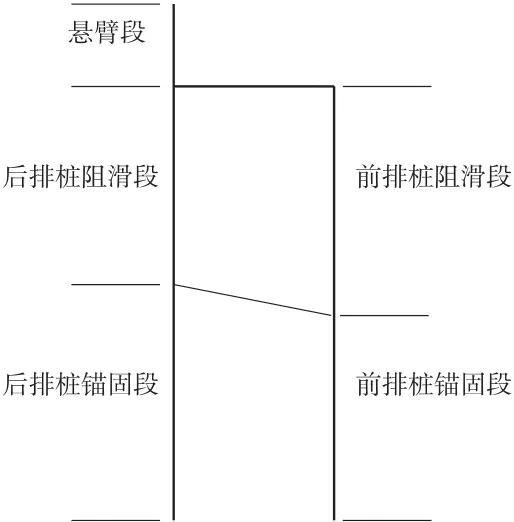
图3　边（滑）坡中的h形桩示意图

简化模型为二维剖面模型，宽约36m，高约30 m，包括滑床岩土体、桩后滑坡体、桩间岩土体、h形抗滑桩和预应力锚杆。h形桩后排桩长21m，前排桩长17.5m，桩体设计参数见表1。

表1　h形抗滑桩桩体设计参数　m

依据模型的尺寸及工程实际情况，运用MIDAS GTS中的网格自动划分功能对模型进行网格划分（见图4）。

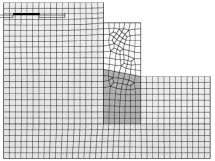
图4　边坡模型网格划分

2.2模型的建立

2.2.1岩土体本构模型的选择

MIDASGTS包含的本构模型多达12种，其中摩尔-库伦模型适用于岩土体弹塑性材料，且能很好地模拟岩土体在剪切破坏条件下的力学变形机理，根据研究内容、模型材料和实际工程情况，选用该模型作为模拟岩土体材料的本构模型，并服从该模型的流动法则。模型中岩土层介质的材料力学性质及特性见表2。

表2　岩土层材料力学设计参数

2.2.2模型的支护结构单元

（1）h形桩。h形支挡结构采用梁单元，每个节点均有3个自由度，在数值计算时，需输入梁的形状、截面积、周长、惯性矩、材料弹性模量、泊松比、材料重度和热膨胀系数等技术参数（见表3）。

（2）锚索。MIDASGTS中有锚杆（索）专用的植入式桁架，将其看作只能承受单轴拉伸的一维线单元，计算时需输入锚索形状、截面积、预应力大小、材料弹性模量、泊松比、材料密度、热膨胀系数等参数（见表3）。

表3　支护结构材料设计参数

2.2.3模型计算区域及边界条件

根据工程实际情况和模型计算需要，采用较简单的二维模型，模型底宽36m，高30m。水平方向为X轴，竖直方向为Y轴，原点位于模型的左下角。

边界约束：模型的底边设置固定支座边界约束，假定其静止不动，不能产生位移和旋转；顶面为自由边界，未加任何约束；模型的前后布置为可动铰支座约束，没有剪应力，其水平方向不能产生位移，但可沿着竖直方向产生位移；模型中不考虑地下水的影响，不考虑渗流作用。

2.2.4模型计算的基本假设

（1）计算区域内的土层材料为均质、各向同性材料。

（2）h形抗滑桩支护结构为弹性材料，满足平面应变问题的基本要求。

（3）土层材料为弹塑性材料，其材料特性如弹性模量、力学性质参数、泊松比等是确定的，不受施工条件的影响。

（4）模型计算不考虑地下水对土层的影响，不考虑地下水渗流作用。

3　数值模型计算结果分析

3.1滑坡模型水平位移和水平应力

采用h形抗滑桩对滑坡体进行加固后，数值软件计算得出的水平位移最大值为11.0mm，出现在坡顶临空面（后排桩桩顶）处，沿着后排桩桩顶以下水平位移逐渐变小直至为零（见图5），滑坡的变形得到有效控制。

图5　h形抗滑桩加固后滑坡模型水平位移云图（单位：m）

模型出现2个应力集中区域，分别位于h形桩前后排桩与滑面交界处的右下区域（见图6），这是因为该区域的土体受到由滑坡推力通过h形桩桩体传递来的作用力，土体受到挤压。

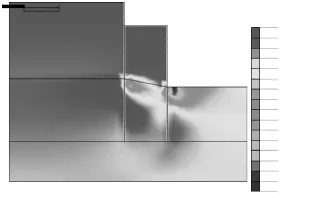
图6　h形抗滑桩加固后滑坡模型水平有效应力云图（单位：kN/m2）

3.2h形抗滑桩桩体位移分析

由于连续横梁能协调前后排桩的变形，前后排桩桩体变形位移基本上是同步的，最大位移出现在后排桩桩顶，为11.0mm（见图7和图8）。在连续横梁的作用下，后排桩连接处和前排桩桩顶位置的位移基本协调，约为8.0mm。沿着桩体向下，水平向位移变形逐渐变小，滑动面以下桩体的变形较小，前后排桩桩底处均出现微小的负向位移（前排桩为-0.002mm，后排桩为-0.004mm）。

图7　前排桩桩体水平位移

图8　后排桩桩体水平位移

3.3h形抗滑桩内力分析

3.3.1h形抗滑桩桩截面弯矩

如图9和图10所示，后排桩桩体最大弯矩出现在桩顶以下约14.0m（滑面以下约2.45m）处，为36170kN·m；前排桩最大弯矩位置与后排桩相似，在前排桩顶以下约12.0m（滑面以下约2.71 m）处，为21320kN·m。

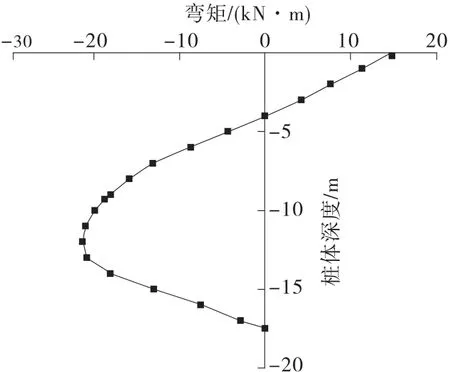
图9　前排桩弯矩图

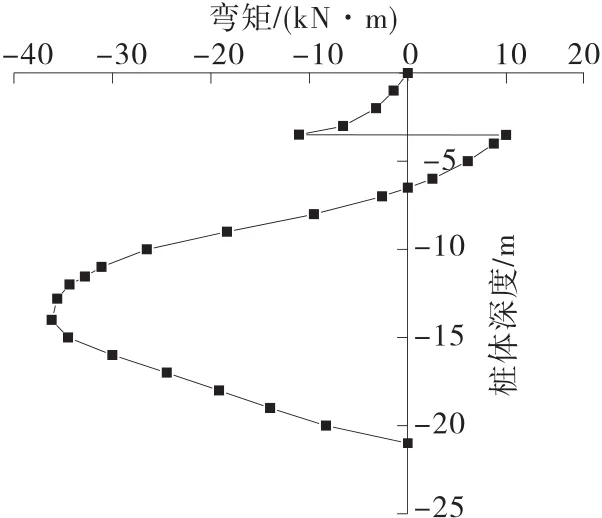
图10　后排桩弯矩图

3.3.2h形抗滑桩桩截面剪力

如图11和图12所示，h形抗滑桩前后排桩桩体最大剪力均出现在桩体与滑面接触处，后排桩剪力最大值为10820kN，位于桩顶以下约11.55m处；前排桩剪力最大值为6230kN，位于桩顶以下约9.3m处。在桩基设计时，应适当强化h形抗滑桩支护结构中应力较集中的部位，避免桩基在滑坡推力作用下发生剪切破坏。

4　桩间距、锚固长度对桩体内力和变形的影响

4.1前后排桩间距对桩体内力和变形的影响

保持数值模型及h形桩其他设计参数不变，变动前排桩的位置，使前后排桩间距分别为3.0、6.5、9.0、12.0、15.0m，计算h形抗滑桩桩体最大水平位移及桩体最大截面弯矩，结果见图13、图14。

图11　前排桩剪力图

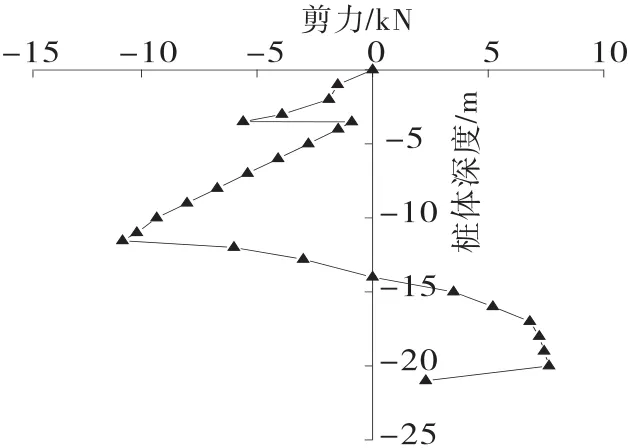
图12　后排桩剪力图

图13　不同桩间距下后排桩最大水平位移

图14　不同桩间距下桩体最大弯矩

从图13可看出：不同前后排桩间距条件下，h形抗滑桩最大水平位移均出现在后排桩桩顶处。随着桩间距的增大，最大水平位移逐渐减小。桩间距从3 m增加到6.5m时，最大水平位移减小速率较大，从11.43mm减小到11.0mm；桩间距从6.5m增加到12m时，最大水平位移减小速率较小且变化率相等（呈直线），最大位移减小至10.67mm；桩间距从12.0 m增加到15m时，最大水平位移减小速率最小，从10.67mm减小到10.65mm。究其原因，当桩间距小于约2b（b为桩体截面宽度，这里b=3m）时，前后排桩间距较小；h形抗滑桩的空间结构形式逐渐趋向于单排桩，其变形特性与一般单排桩类似，桩体水平位移较大；随着桩间距增大至2b～4b（6.0～12.0m），连续横梁的长度及桩间岩土体的宽度较大，h形桩开始发挥其独特的抗滑性能，抵抗水平变形的能力较大，桩顶水平位移较小；桩间距大于4b（12.0m）时，增大桩间距对于减少桩顶位移的贡献较小，h形抗滑桩抵抗水平变形的工作效率变低。因此，建议h形抗滑桩前后排桩间距取2b～4b。

从图14可看出：随着h形抗滑桩桩间距的变化，桩体最大弯矩基本没有变化，曲线水平向延伸较平缓，说明改变前后排桩间距对于h形抗滑桩桩体最大弯矩的影响较小。

4.2锚固长度对桩体内力和变形的影响

保持模型其他参数不变，改变基桩锚固长度，分别为6.0、7.0、8.0、9.45、11.0、12.0m，研究h形抗滑桩桩体在不同锚固长度下桩体最大位移和最大弯矩。

如图15所示，随着锚固长度的增大，桩顶最大位移减小，但当锚固长度增加到一定长度（9.5m）后，桩顶位移的变化较小或基本不变，继续增加锚固长度对提高h形桩抗滑性能的作用甚微。当锚固长度从6.0m增加到9.5m时，桩顶最大位移减少5.32mm；而当锚固长度从9.5m增加到12.0 m时，桩顶最大位移仅减少0.2mm。建议锚固长度取1/3～1/2桩长。

图15　不同锚固长度下桩体最大位移

如图16所示，锚固长度从6.0m增加到12.0 m，桩体的最大弯矩基本不变，说明通过改变锚固深度不能明显调整桩体最大弯矩。

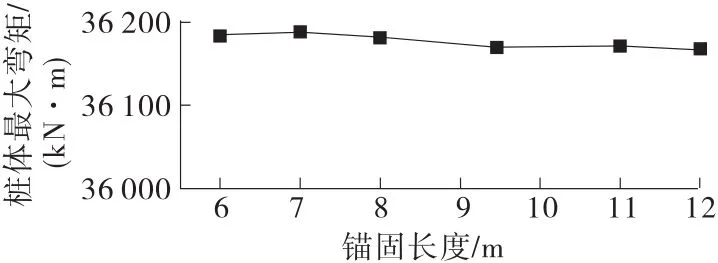
图16　不同锚固长度下桩体最大弯矩

5　结论

且前后排桩体变形协调；在h形桩前后排桩与滑面交界处的右下区域出现应力集中现象，现场施工设计中应对该区域的岩土体进行加固。

（2）前后排桩桩体最大弯矩均出现在滑面以下约2.5m处，最大剪力出现在滑面附近。

（3）桩间距小于2b时，桩顶位移较大；桩间距大于4b（12.0m）时，增大桩间距基本不会减小桩顶位移。建议前后排桩间距取2b～4b。改变桩间距对桩体最大弯矩的影响不大。

（4）随着锚固长度的增大，桩顶最大位移减小，达到一定值后保持不变，建议锚固长度取1/3～1/2桩长。不同锚固深度下桩体最大弯矩基本相等。

［1］ 郑颖人，陈祖煜，王恭先，等.边坡与滑坡工程治理［M］.第二版.北京：人民交通出版社，2010.

［2］ 王羽.h形抗滑桩设计计算方法研究［D］.成都：成都理工大学，2011.

［3］ 欧明喜.h形抗滑桩力学机理及其工程应用研究［D］.重庆：重庆大学，2012.

［4］ 周金成.h形抗滑桩受力机理分析及工程应用［D］.重庆：重庆交通大学，2012.

［5］ 肖世国.边（滑）坡治理中h形组合抗滑桩的分析方法及工程应用［J］.岩土力学，2010，31（7）.

［6］ 欧孝夺，唐迎春，崔伟，等.h形抗滑桩模型试验及数值模拟［J］.岩石力学与工程学报，2012，31（9）.

［7］ 孙涛，刘俊岩，刘燕.双排桩支护排距的优化研究［J］.岩土工程学报，2012，34（增刊）.

［8］ 张永杰，李侑军，曹文贵，等.大型滑坡预应力锚索h形抗滑桩处置方法研究［J］.水文地质工程地质，2014，41（5）.

［9］ 戴自航.抗滑桩滑坡推力和桩前滑体抗力分布规律的研究［J］.岩石力学与工程学报，2002，21（4）.

［10］ KourkoulisR，GelagotifF，AnastasopoulosI，etal. Slopestabilizingpilesandpilegroups：parametric studyanddesigninsights［J］.JournalofGeotechnical andGeoenvironmentalEngineering，2011，137（7）.

［11］ JTGD63-2007，公路桥涵地基与基础设计规范［S］.

［12］ 赵海玲，彭盛恩，王启智.滑坡成因机制分析及治理措施［J］.铁道建筑，2004（9）.

［13］ 马青力.h形桩板墙桩土相互作用数值分析［D］.成都：成都理工大学，2006.

［14］ 张泽坤.h形抗滑桩的有限元分析［D］.成都：西南交通大学，2008.

（1）桩体最大水平位移出现在后排桩桩顶处，

U418.5

A

1671-2668（2016）04-0136-05

2016-03-24