降雨入渗对顺层边坡稳定性的影响研究

姚童刚

（湖南长益高速公路有限公司，湖南长沙 410006）

降雨入渗对顺层边坡稳定性的影响研究

姚童刚

（湖南长益高速公路有限公司，湖南长沙 410006）

雨水的入渗作用对顺层岩质边坡的稳定性有较大影响。文中在分析降雨入渗过程的基础上，采用立方定律及光滑板模型等理论对降雨入渗作用下岩体受到的拖拽力、渗透力进行了求解；通过雨水入渗条件下边坡稳定性分析验算，依据达西定律，提出了以边坡裂隙冲水高度和降雨强度为指标判定边坡稳定性的方法，并对其进行了求解。

公路；降雨入渗；顺层边坡；水力作用；稳定性判定

中西部山区是目前中国高速公路建设的重点区域，在这些地方修建高速公路会遇到大量人工高边坡，边坡的稳定性成为工程的关键。顺层边坡是人工高边坡中稳定性较差的一种边坡，在降雨入渗、人工开挖扰动等因素的作用下很容易发生变形破坏。但由于顺层边坡工程地质条件复杂、脆弱，其稳定性分析与判定一直是公路界的难题，已逐步成为影响高速公路发展的棘手问题。目前，虽然国内外众多专家、学者对顺层边坡稳定性进行了分析，但成果较少，难以满足需要。该文基于达西定律，分析雨水入渗至边坡过程中顺层边坡受到的力学作用，推导相关水力作用的计算方法，并基于边坡的稳定性验算推导顺层边坡稳定性评价指标的计算方法。

1　降雨入渗过程分析

降雨入渗的发展历程分为通量控制和坡体表面控制两个阶段。起始阶段为通量控制阶段，此时边坡岩（土）体含水率较低，但梯度较大，渗入率较高，一般不会产生坡面径流。随着雨水不断渗入坡体，边坡岩（土）体含水率逐步增加，含水率梯度逐步下降，入渗率也不断减小。当降雨强度大于岩（土）体渗入速度时，坡体表面会出现积水或形成地表径流，形成有压入渗，此为第二个阶段，即坡体表面控制阶段。当边坡坡面出现积水或径流时，坡面含水率自上而下可划分为饱和区、过渡区、传导区及湿润区（见图1）。

2　渗流作用下边坡力学分析

2.1渗流对裂缝孔壁的作用力

图1　岩（土）体含水率随雨水入渗的变化

雨水在裂缝空隙间的流动会对岩体周围裂隙孔壁产生拖拽力，随着时间的推移，这种拖拽力会加剧边坡裂缝的发展，最终导致边坡破坏。该作用力可采用光滑板模型和立方定律进行求解，其基本假设为渗流状态稳定、温度处于恒定状态。采用光滑板模型计算这种单裂隙不可压缩流体的单相饱和渗流问题，可将其天然粗糙的裂隙表面设想为一组有固定宽度（b）的光滑且无限延伸的平行板（见图2）。

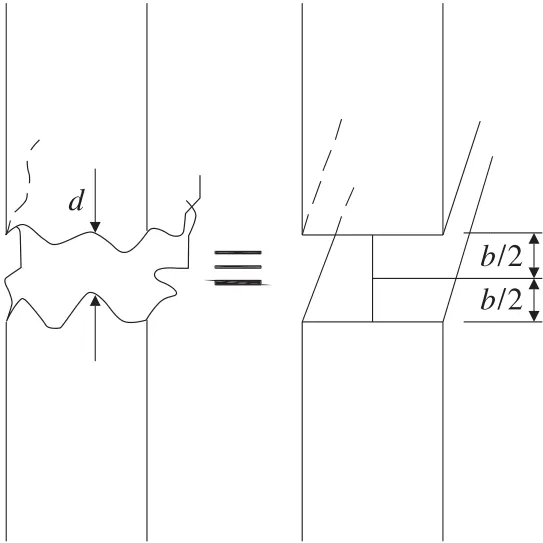
图2　平行板模型示意图

根据流体力学连续性方程及平行板模型计算的假定条件，单裂隙的泛定方程可表示为：

单裂隙渗流的边界条件为：

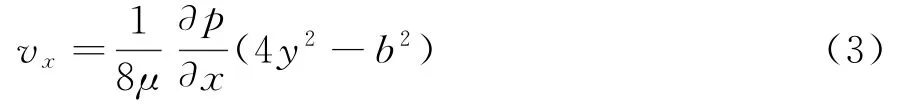
令水流压力梯度Jp=-∂p/∂x且p=γ（HZ），则：

通过式（1）、式（2），采用解析法求得单裂隙中流体（水流）沿x方向流动的分布函数为：

将式（3）代入式（4），得：

式中：γ为液体的重度；μ为液体的动力粘滞系数；Jf为水力梯度。

由式（5）可知：裂隙水流速度vx是一个与x轴无关的抛物线，即在任意一个断面上，裂隙水流速度均无变化，据此可得裂隙断面单位宽度水流量为：

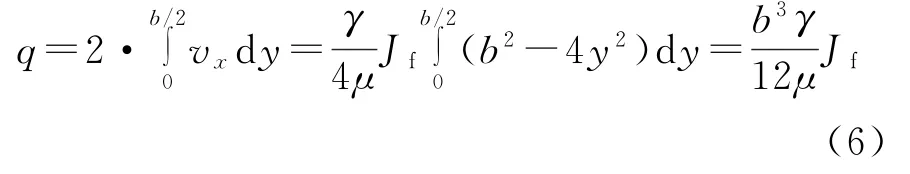
根据式（6），裂隙缝宽的立方跟裂隙的单位宽度内水流量成正比关系，据此可得在单裂隙裂缝中渗入的水流水平流速为：

式中：Kf为裂隙的渗透系数，Kf=b3γ/（12μ）。

将裂隙中任一段经由水流的带状体作为研究对象进行分析，其受力情况见图3。

图3　空隙水流作用力示意图

根据恒定总流动量方程，图3中长度为dx的流体在x轴方向上所受到的各种力可表示为：

式中：ρ为流体（水）的密度；q为流经单位裂隙宽度内的水流量；β2、β1分别为流体在x+dx断面和x断面的动量修正系数；¯vx1、¯vx2分别为流体在x断

2.2降雨入渗对岩体的渗透力

在水力梯度的作用下，流经岩体空隙中的流体会受到很大的阻力。当水渗出时，岩体颗粒会对水流产生摩擦作用，与此同时，水会对岩体颗粒形成反方向的渗透力。水对岩体产生的渗透力是导致边坡稳定性降低的另一重要因素。在岩体中选长度为dl、横截面积为dω的一段流束，岩体孔隙率为n（见图4），则该段流束受到的作用力包括空隙间水的自重γwndωdl、岩体颗粒对水流的摩擦力F及流束两端的孔隙水压力p和p+dp。面和x+dx断面的平均流速；∑Fx为流体在dx裂隙段内所受各种作用力在x轴方向上分量的代数和。

由上面的分析可知，式（8）等号左边为零，即∑Fx=0，则有：

式中：p为x断面流体静水压力；p+dp为x+dx断面流体静水压力；tm为裂隙水流所受到的裂隙壁的阻力。

将p=γ（H-Z）代入式（9），整理并简化得：

图4　渗流流束受力示意图

由司托克斯公式可知，渗流途径上的单个岩体颗粒所受到的流束对其的阻流阻力可表示为：

f=λμv′d（11）式中：λ为修正系数；μ为相邻岩体颗粒之间的影响系数，对于处于无限水体中的圆球，μ=3π；v′为孔隙水的流速；d为岩体颗粒的直径。

如果流经岩体的分散体总量为N，则：

式中：V为流经岩体的分散粒的总体积；m为单个岩体颗粒的体积；β为球体系数。

此时，岩柱受到的流束渗透总阻力可表示为：

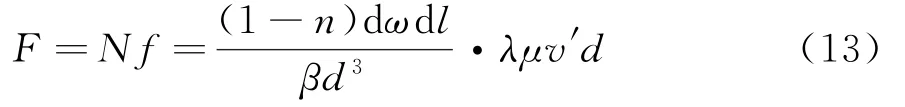
根据图4，由力平衡条件可得：

3　边坡稳定性分析

3.1边坡渗水条件下的稳定性验算

以后缘张裂型顺层岩质边坡为研究对象，在雨水渗入到坡体的过程中，岩体会受到流体对裂隙壁的拖拽力T、流体的阻力F、张拉裂隙内的静水压力V、软弱滑带上的静水压力U及滑体的自重G（见图5）。

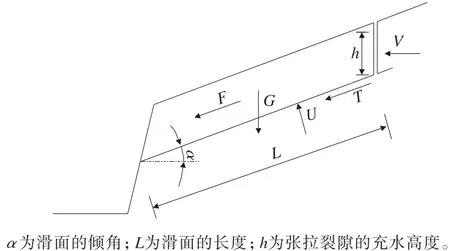
图5　渗水过程中坡体稳定性力学分析模型

取缝隙渗流方向上的任意段长度坡体进行分析，可知：

根据边坡稳定性计算方法，降雨入渗条件下顺层边坡稳定性可按下式计算：

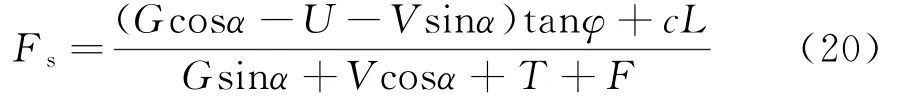
式中：φ为软弱滑带上饱和土的内摩擦角；c为软弱滑带上饱和土的粘聚力。

由式（20）可知：在降雨入渗条件下，顺层边坡抗滑力会降低，下滑力会增加，导致边坡安全系数减小、稳定性降低。

3.2边坡稳定性判定指标计算

处于极限状态的边坡其安全系数为1，将式（16）～（19）代入式（20），得到岩体后缘张拉裂隙极限充水高度hcr在极限平衡状态下的表达式：

根据式（21），当裂隙中充水高度h＜hcr时，边坡处于稳定状态；h＞hcr时，边坡会发生变形破坏。

根据达西定律，渗流量可由下式求得：

式中：A为渗流面积。

当hcr达到极限值时，坡面的极限渗流量Qcr可表示为：

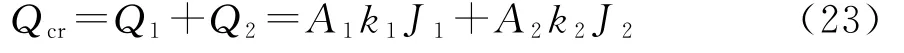
式中：Q1为岩体内渗流量；Q2为软弱滑带上渗流量；A1为岩体渗流面积，A1=hcr；k1为岩体的渗透系数；A2为软弱滑带上渗流面积，A2=b；k2为软弱滑带上渗流系数。

根据上面的求解，k2=b3γw/（12μ）；岩体和软弱滑带上的水力梯度J1、J2都为hcr/L，对式（23）进行转换，得：

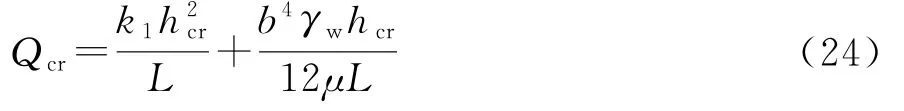
刘才华等经过研究分析得出坡体裂缝张开处的水流汇集量为：

式中：ψ为径流系数；q为降雨强度；A为汇水面积。

令Q0=Qcr，并将式（24）、式（25）代入，可得到张拉裂隙临界充水高度hcr与临界降雨强度qcr之间的关系式：

在岩体完整性较好、致密、裂隙不发育的情况下，可将渗流量忽略不计，式（26）可简化为：

综上所述，可将降雨强度及坡体裂隙中渗入水柱体的高度作为评判边坡稳定性的指标，判断标准见表1。

表1　边坡稳定性的判断

4　结论

（1）雨水渗入坡体的过程可看作是一个由饱和到非饱和的过程。岩体的渗水性能与流经坡体的雨量及方式都会影响入渗强度，如果降雨强度小于岩体的入渗强度，则渗流强度由降雨强度决定；当降雨强度大于岩体入渗强度时，渗流强度由岩体的入渗强度决定。

（2）当顺层边坡产生后缘张拉裂缝时，岩体会受到静水压力、渗透力及裂缝孔壁拉力的作用。基于立方定律和光滑板模型理论，利用极限平衡定理公式，得出拖拽力tm=bγ/2Jf，由司托克斯公式得出渗透力F=γwndωdl。

（3）岩体空隙在渗流状态下作用着各个方向上的力，采用极限平衡理论，可推导出顺层边坡稳定性系数的计算公式。同时依据裂缝张开处的水流汇集理论，可以降雨强度和后缘张拉裂隙充水高度作为判断边坡失稳破坏的标准。

［1］ 邓桂荣，周德培，李安红，等.顺层岩质边坡不稳定岩层临界长度分析［J］.土木工程学报，2014，24（2）.

［2］ 张有天，周维垣.岩石高边坡的变形与稳定［M］.北京：中国水利出版社，1999.

［3］ 杨天鸿，张峰春，于庆磊，等.露天矿高陡边坡稳定性研究现状及发展趋势［J］.岩土力学，2011，32（5）.

［4］LiouTai-sheng.Statisticalanalysisofliquidseepageinpartiallysaturated，heterogeneousfracturesystems［D］.San Francisco：UniversityofCaliforniaatBerkeley，1999.

［5］茅春浦.流体力学［M］.上海：上海交通大学出版社，1995.

［6］ 刘才华，徐健，曾传林，等.岩质边坡水力驱动型顺层滑坡破坏机制分析［J］.岩石力学与工程学报，2005，24（19）.

U416.1

A

1671-2668（2016）04-0104-03

2016-04-16