Modeling and Sliding Mode Control with Boundary Layer for Unmanned Coaxial Rotor Ducted Fan Helicopter

Chen Zhi，Wang Daobo，Zeng Ziyang，Wang Biao

College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China（Received 27January 2015；revised 18August 2015；accepted 2September 2015）



Modeling and Sliding Mode Control with Boundary Layer for Unmanned Coaxial Rotor Ducted Fan Helicopter

Chen Zhi，Wang Daobo＊，Zeng Ziyang，Wang Biao

College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China
（Received 27January 2015；revised 18August 2015；accepted 2September 2015）

The structure and modeling of a novel unmanned coaxial rotor ducted fan helicopter（RDFH）are introduced，and then，based on the helicopter air dynamics and kinematics principles，a nonlinear model of the coaxial rotor ducted fan helicopter is developed and implemented on the basis of the wind tunnel experiment.After that，the helicopter′s stability and coupling characteristics of manipulation are analyzed through time-domain.Finally，a sliding mode controller（SMC）with boundary layers is developed on a hardware in the loop platform using digital signal processor（DSP）as the flight control computer.The results show that the RDFH′s tracking ability performs well under the use of proposed controller.

modeling；coaxial；rotor ducted fan helicopter（RDFH）；time-domain analysis；sliding mode controller（SMC）

0 Introduction

Unmanned aerial helicopter（UAH）control has been considered as a challenge in aeronautical field over decades.The main difficulties，in designing controllers for UAH，can be generally characterized as open-loop instabilities，cross-coupled，underactuated，large uncertainties，and highly nonlinear dynamics［1，2］.Although there are so many difficulties，many researchers still motivated to resolve them.On one hand，the researchers are very interested in the unmanned helicopter application in practical engineering.On the other hand，nonlinear characteristics of the unmanned helicopter（Such as the nonlinearity of the dynamics and the strong coupling between the forces and torques produced by the vehicle actuators）is very suitable as a hotbed of experimental nonlinear controller.

Wang［3］talked about the control of hovering mode of a linearized helicopter model，but did not refer to the full envelope flight control.Rafferty［4］studied the control of longitudinal and yaw attitudes，but vertical and lateral motion did not be involved.Fu et al.［5-7］elaborated the full envelope flight control，but the application object is a miniature helicopter.The properties of the coaxial rotor ducted fan helicopter（RDFH）are different from those common helicopters.

Therefore，it is necessary to design a controller based on the analysis of the coaxial rotor ducted fan helicopter′s characteristic［8-10］.And it has the ability to realize stability augmentation control，attitude control，heading control，height control，automatic landing control，and beyond visual range autonomous tracking control.

1　Mathematical Model

1.1 Configuration of novel helicopter

The coaxial rotor ducted fan helicopter is a special configuration helicopter.The main structures are shown in Fig.1，which are composed byrotor，duct fan，fuselage，landing gear，power，and avionics systems.

Fig.1　Structure of coaxial rotor ducted fan helicopter

There are so many differences between the novel helicopter and common helicopter.Firstly，the novel helicopter uses the layout of the rotor fan coaxial type，and both the main rotor and the fan provide the lift forces（The main rotor provides most of them while others are provided by the fan）.By changing the rotor collective pitch，longitudinal and lateral cyclic pitches，the helicopter can realize height and position control. While the heading control can be realized by the differential torque between main rotor and the fan.Novel helicopter abandons the traditional form of the tail rotor for the benefits of decreasing the size，enhancing the rate of engine work，and reducing the incidence of tail rotor transmission failure.Secondly，the whole machine adopts the symmetrical layout.By using the axial symmetry structure，it is not easy to turnover while landing.Finally，the main moving parts and bearing parts are manufactured by composite materials，so the total weight of the helicopter is lighter，and the radar wave transmission and stealth performance are stronger.

1.2 Nonlinear mathematic model

Helicopter is a complicated dynamic system，essentially it belongs to the multi-body dynamics system.Due to the aerodynamic characteristics and structure of the components，as well as the relations between the aerodynamic parameters are complicated，it is a hard work to analyze and calculate the accurate mathematical description.

Practice has proved that，if the helicopter is seen as dynamic system by the following two parts，many aerodynamics problems can be solved.The first part is the rigid body，on which it has a direct force and moment produced by the fuselage.The second part is the lifting system，including the rotor and the fan.In this case，the helicopter is made up of three parts：Rotor aerodynamic model，fan aerodynamics model，and fuselage aerodynamic model.Both the rotor and the fan aerodynamics model are established for the purpose to describe their force and moment effect to the fuselage.

We define the positive direction of the body axis like this：X-axis is forward，Y-axis is rightwards and Z-axis is downward.Under this body axis system，the force and moment distribution of the novel helicopter is shown in Fig.2.Fx，Fy，Fzare the force distribution of joint forces generated by the rotor，duct fan and fuselage.τx，τy，τzare the torque distribution of joint torques caused by the rotor，duct fan and fuselage.u，v，wrepresent the speed of the barycenter on the body axis，called Xspeed，Yspeed and Zspeed，respectively.φ，θ，ψare the Euler angles，and p，q，rthe angular rates.

Fig.2　Coordinate system of coaxial rotor ducted-fan helicopter

For conventional helicopter，the OXZplanar of the body coordinate system is longitudinal symmetry，so the inertia product Ixy=Iyz=0.And Ixz=0because of the symmetric along OYZplanar in the novel helicopter.According to Newton′s laws of mechanics and the law of rigid body rotation，adding the coordinate transformation formula，we have 6degrees of freedom and 12states ofthe full amount of nonlinear mathematical model

where″c″and″s″represent cos and sin，respectively.

where Mis the quality of the whole machine and gthe gravitational acceleration.Ix，Iy，Izare the inertia moment along body axis.Fx，Fy，Fzin Eq.（2）andτx，τy，τzin Eq.（4）reflect its special characteristics of RDFH.Thus the above work of establishing the nonlinear mathematic model is necessary，or it will hard to analyze the helicopter quantificationally.

2　Helicopter Dynamics Analysis

To analyze the characteristics of coaxial rotor ducted fan helicopter，the response of the states is be seen in the case of no controller input.We will analyze the zero input response as well as coupling characteristics between the channels.

2.1 Open loop zero input response

For common helicopter，the roll angle is not equal to zero when the helicopter is in the hover state，for reasons that the tail rotor is higher than the helicopter center of mass.It will generate rolling moment.In order to balance this rolling moment，helicopter needs to tilt about 3degrees. But for our coaxial rotor ducted fan helicopter，all of the Euler angles equal zero in the hover state because of the symmetrical layout，and the fan which take the place of tail rotor will generate an-ti-torsional moment.But this kind of stable cannot last for a long time.When a slight change in the attitude，the novel helicopter will deviate from the equilibrium state.

Here we assume that a given initial pitch angle and roll angle is 0.001rad.From Fig.3we can see that roll angleφ（phi）increases firstly，producing the force to let the helicopter move to the right，and the lateral velocity v also increases.With the increase of speed，resistance force of the fuselage increases gradually.Because the resistance force bearing point on the helicopter is above the center of mass，it can produce negative roll moment，and correspondingly the roll angle φ＜0.It will produce the force to the left，forcing the lateral velocity v of the helicopter shrink to less than 0.In this case，the helicopter will move to the left.Repeatedly，the helicopter will move from side to side several times before it is out of control.

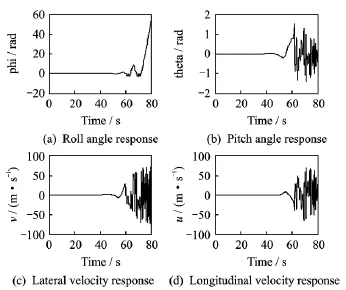
Fig.3　Open loop zero input response

2.2 Coupling characteristics between channels

2.2.1 Influence of rotor collective pitch manipulate

After applying unit step signal to the rotor collective pitch，and the other input channels are zero，from Fig.4（a）we can see that the vertical speed w，the yaw angularψ（psi）and the yaw angular rate r are all have response（The unit of angular and angular rate are all degree）.For the positive rotor collective pitch of control input，the helicopter vertical speed will increases，and this isconsistent with actual helicopter response.When the rotor collective pitch increases，the blade angle of attack will increase too.Under certain revolving speed，the rotor will generate greater thrust，and the vertical accelerated speed will also increase.The vertical speed wto the response of the rotor collective pitch input is stable，and it will eventually tend to a steady value.It shows that the relations between them are a first-order inertia.

The change of yaw angularψ（psi）and the yaw angular rate r comes from the increasing torque which is generated by the rotor collective pitch，and if there is no counteractive to offset this torque，the heading of the helicopter will change.It shows that vertical movement of the novel helicopter is coupling with the yaw movement.

2.2.2 Influence of longitudinal cyclic pitch manipulate

In Fig.4（b），longitudinal cyclic pitch input is given as 1degree，and the other input channels are given as 0degree.It leads to the response of pitching angleθ（theta），pitching angular rates q and the linear speed uin the Xaxis.Meanwhile，the rolling angleφ（phi），pitching angular rates p and the linear speed v in the Y axis are also changed.Relatively，the body axis angular velocity and attitude angle change rapidly，while the forward speed and lateral line speed change slowly.

2.2.3 Influence of lateral cyclic pitch manipulate

In Fig.4（c），longitudinal cyclic pitch input is given as 1degree，and the other input channels are given as 0degree.The response curves，are similar to those of the longitudinal control（Plus or minus sign is different from the definition of the coordinate system）.

2.2.4 Influence of fan collective pitch manipulate

Yawing of conventional helicopter is implemented by changing the tail rotor collective pitch. Therefore，there is no cross-coupling between height and yaw.But the novel helicopter is not the same.The fan provides not only the yaw control input，but also the lift force.The change of the heading must have impact on the height.As it is shown in Fig.4（d），when the helicopter is in the hover state，adding the fan collective pitch can cause the yaw angleψdecrease.Meanwhile，The″Z″in Fig.4denotes the height curve，and itspositive direction is downward.Therefore，the actual physical meaning of curve Zshows the helicopter is climbing slowly.

Fig.4　Step input response curves

In short from what is discussed above，we may safely draw the conclusion that there are serious cross-coupling between the longitudinal and the lateral，as well as between the heading and the vertical.The strong coupling between longitudinal and lateral，as well as the coupling between heading and vertical makes the decoupling work difficult to achieve good control performances，and it also increases the difficulty to design the flight control system.

3　Control System

Inspired by Dale Enns［11］，we focus our attention on a cascade control structure（See Fig.5）constituted by four loops，such as position loop，velocity loop，attitude loop，and angular rate loop.All these subsystem constitute a nested cascade controller.

The design of each controller follows the same theory，named sliding mode control with boundary layers，but for the subsystem states and control outputs are changed.Due to space limitations，all the details of each subsystem′s design process for a whole control system in RDFH are too redundant to show in this paper.For the purpose of concise and clear，position loop is used as an example to explain the design process with boundary layers of sliding mode control（SMC）. The rest loops will only give out the design block diagram and the controller parameter，the design process will not list out in detail.

3.1 Position and velocity loop control

Fig.6shows the position and velocity loop. Mathematical expressions for position loop are given in equation.In this subsystem，position errors xerr，yerr，zerrare given as subsystem states；velocities uref，vref，wrefare given as control output.As shown in Fig.6，the position controller outputs uref，vref，wrefas the velocity controller reference inputs are fed to the velocity controller. It needs to be stressed the amplitude limiting markers in Fig.6.According to the previous work we know that the lift force and resistance of RDFH rapidly increase with the increase of the speed and changing in a nonlinear way.As a lifting system，RDFH is suitable for hovering and flying in a low speed.Therefore，the amplitude limiting is added to the velocities uref，vrefand wref.

Fig.5　Control scheme block

Fig.6　Position and velocity loop

To avoid the complexity，formulaX= f（X）+g（X）·Uis used to replace the following equation

Since the controlled object has been described clearly，SMC with boundary layers controller for position loop in RDFH helicopter can be designed as follows：

Step 1 The switching surfaces are given as follows

where Ck=diag｛0.4，0.4，0.4｝，S（X）=［Sx，Sy，Sz］T.

Step 2 The approaching law of SMC with boundary layers is given as follows

where k1=diag｛1，1，1｝，k2=diag｛0.001，0.001，0.001｝，the approaching law in Step 2 does not use the sign（·）function as usual but use tanh（·）function instead.This is because sign（·）function is a discontinuous function.If the control input U contains the discontinuous function，Uis discontinuous，too.

Step 3 Based on the switching surfaces in Step 1and approaching law in Step 2，the position controller can be designed as follows

The flight path tracking control system is constituted under the use of the position controller，cooperatively a differential GPS is in use as the position feedback information.The subsystem not only can inhibit the influence such as flight speed，air temperature，wind，etc，but also can be used as a navigation and positioning information.In this way，UAH can fly automatically according to the pre-set flight path.

The velocity loop is also shown in Fig.6on the right half.Equations for this loop are given. The subsystem is utilized to track reference velocity uref，vref，wreffrom position loop.Velocity errors uerr，verr，werrare given as subsystem states；Euler anglesφref，θrefand collective pitch of the main rotorδcolare given as control outputs.It means that the designed controller should send reference Euler anglesφref，θrefand collective pitch δcolto the attitude loop.

3.2 Angular rate and attitude loop control

Stability is a prerequisite and key for automatic control.But the unmanned helicopter is essentially an unsteady controlled object.In the design of the autopilot，we have to adjust the damping characteristics of unmanned helicopter and turn unstable，uncontrollable object to stable and controllable object.Using the speed feedback closed loop control method can effectively increase the damping characteristics of controlled object and control quality，and it can achieve the goal of increasing control stability.The novel helicopter damping stability augmentation control consists of three parts，which are the heading angle rate control，the pitching angle rate control，and the rolling angle rate control.

Equations for angular rate loop are given.In this subsystem，angular rate errors perr，qerr，rerrare given as states，longitudinal and lateral cyclic pitchesδaandδb，and collective pitch of the fan rotorδfanare given as control outputs.

Damping stabilization control is not enough to achieve the purpose of the autopilot，because the helicopter will be affected by wind，airflow，and many other factors.The damping stabilization control cannot correct the deviation automatically.In the case of making the helicopter stable and controllable，we use the yaw angle position sensor and the pitch and roll attitude position sensor to constitute the attitude close-loop control. That is why the attitude controller is presented in Fig.7.In this way，the helicopter can fly at a certain attitude，and this is the most important aspect of autopilot for an unmanned helicopter.

The Euler angle loop is shown in Fig.7.Equations for this loop are given.In this subsystem，attitude errorφerr，θerr，ψerrare given as states and reference angular rates pref，qref，rrefare given as control outputs.It means that the designed controller should send the reference angu-lar rates pref，qref，rrefto angular rate loop，as shown in Fig.7.The design theory of attitude loop is exactly the same as the velocity loop.All the controller design parameters are presented in Table 1.

Fig.7　Angular rate and attitude loop

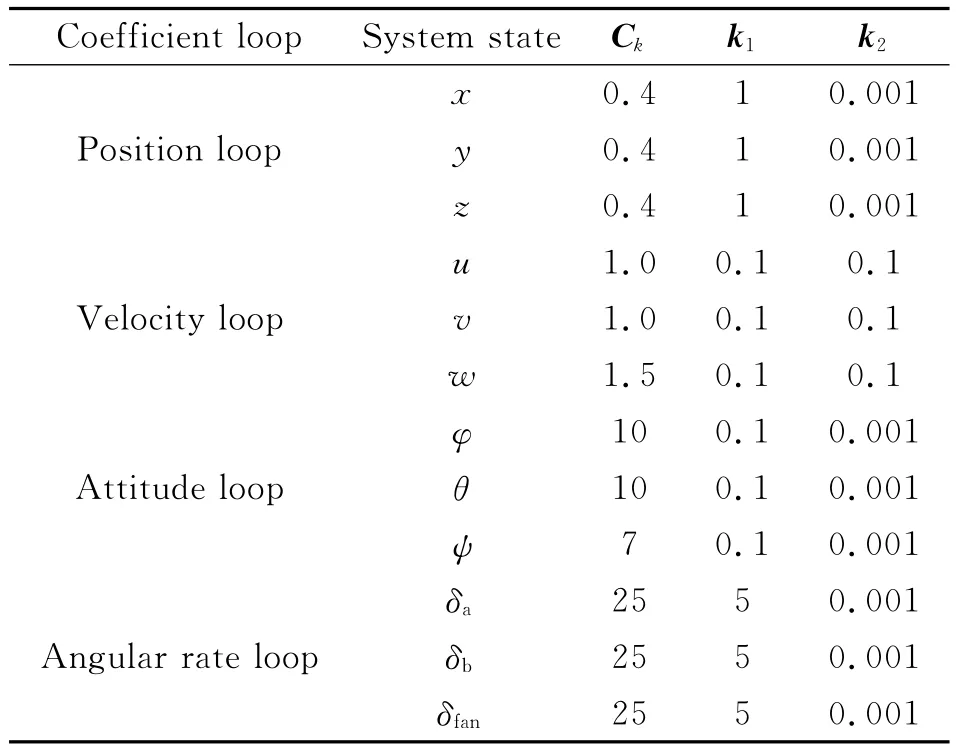
Table1　Controller design parameters in different loops

4　Numerical Simulation Results

Unmanned helicopter is a complex object which has many unknown characteristics.In engineering，it is dangerous to fly directly according to the previous analytical method.To reduce the risk and ensure the reliability of flight test，the simulation test is necessary.In this paper we present the simulation structure of RDFH and obtain the results with the simulation.

The numerical simulation is a process in which the mathematical model is running on the computer.In this process，the controller is the flight control computer（TMS320F28335is used as the core component，and its highest frequency is up to 150MHz），and its design steps which are shown in Section 3.1are written by means of software using C computer language.The nonlinear mathematic model is used to substitute the real controlled object RDFH.Considering the controlled object is simulated by computer in the form of mathematical model，and it does not like the real physical system which needs to drive the actuator.Thus the servo drive parts can be removed，and the output of the flight control computer can be send to the simulation computer directly.Meanwhile，the output of the simulated signal from the simulation computer can be send back to the flight control computer.Full digital simulation structure is shown in Fig.8.

Fig.8　Full digital simulation structure

As it is shown in Fig.8，the numerical simulation system contains remote telemetry system，the flight control system，and the simulation computer.After the initial states are determined，the mathematic model in the simulation computer is running.The remote telemetry system collects the flight control commands，and sends them to the flight control computer by means of serial port.The flight control computer parses these reference control commands to determine theflight mode.Meanwhile，comparing the flight data with these reference commands，the closedloop feedback control is realized according to the control law.In this way，the output results of the control law are sent to the simulation computer as the model inputs every 20ms.The simulation computer calculates the next states via the flight dynamics model，and sends them back to the flight control computer via serial port every 20 ms.At the same time，the flight control computer sends the flight data to the ground remote telemetry system via serial port every 100ms to facilitate the real-time monitoring of the flight simulation.

The trajectory tracking curves are shown in Fig.9.The helicopter takes off at the 10th second.After reaching the predetermined height of 20m，the helicopter flies forward for 5m，and then it moves backwards for 5m.At the 40th second，helicopter moves to the right，and then returns from the 5min the Yaxis.Finally，the helicopter lands down to the ground.In the process，heading angle always stays to 0.

In Fig.9，we can see that the line z reaches -20min less than 10s.Without limiting the rate of climb，which is 3m/s shown in Fig.10（a），the helicopter can reach the predetermined height within a shorter time.The lines Xand Y response in the position loop can follow the given reference in no more than 5s，and the biggest value of the attitude response shown in Fig.11（b）conforms to the real state of flight.

As it is shown in Fig.11，the attitude control effects are perfect by means of the attitude controller.The roll，pitch and yaw channels are all followed their own reference inputs timely.

To sum up，it can be seen from Figs.9—11 that the RDFH′s tracking ability performs well under the control of nested cascade controller，and the crossed-couplings between different channels are suppressed effectively.Therefore，the controller designed by SMC with boundary layer approach is proven to be a success.

Fig.9　Trajectory tracking curves

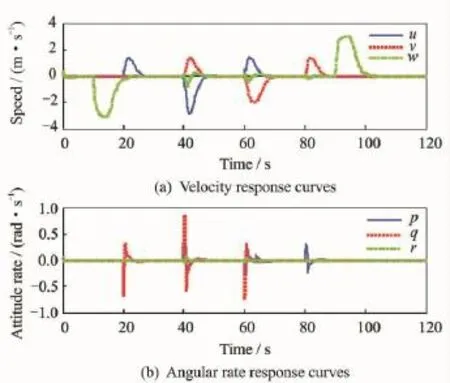
Fig.10　Speed and attitude rate curves while tracking

Fig.11　Attitude and its reference curves

5　Conclusions

In this paper，we focus on the modeling and control of a novel helicopter.The main contribution of this paper is to carry out a mathematical presentation for RDFH，which offers an environment for flight dynamics analysis and controller design.Though SMC with boundary layer technique is an effective control method for the RDFH，further research needs to be investigatedwhen the effect of inner uncertainties and external disturbance are urging on the helicopter.

Acknowledgements

This work was supported by the National Natural Science Foundation of China（Nos.61304223，61374116，61503185）and Specialized Research Fund for the Doctoral Program of Higher Education（20123218120015）.

References：

［1］ PADFIELD G D.Helicopter flight dynamics：The theory and application of flying qualities and simulation modelling［M］.Washington，USA：AIAA，1996：1-13.

［2］ GONG H J，YANG Y D.Design and implementation of gust response alleviation control system for helicopters［J］.Transactions of Nanjing University of Aeronautics &Astronautics，2004，21（1）：13-17.

［3］ WANG H Q，WANG D B，NIU X W，et al.Modeling and hover control of a novel unmanned coaxial rotor/ducted-fan helicopter［C］∥Proc of the IEEE International Conference on Automation and Logistics.Jinan，China：IEEE，2007：1768-1773.

［4］ RAFFERTY K J.A comparison of PID and sliding mode controllers for a remotely operated helicopter［C］∥12th International Conference on Control，Automation，Robotics &Vision.Guangzhou，China：IEEE，2012：984-989.

［5］ FU Jian，CHEN Wenhua.Sliding mode control for a miniature helicopter［C］∥Proceedings of the 17th International Conference on Automation &Computing.［S.l.］：IEEE，2011：98-103.

［6］ LORENZO M.Robust full degree-of-freedom tracking control of a helicopter［J］.Automatica，2007，43：1909-1920.

［7］ FU Jian，CHEN Wenhua.Chattering-free sliding mode control with unidirectional auxiliary surfaces for miniature helicopters［J］.International Journal of Intelligent Computing and Cybernetics，2012，5（3）：421-438.

［8］ CHEN Wei，LU Jingchao.Robust sliding mode control law design for the lateral model of a helicopter［C］∥Sixth International Conference on Measuring Technology and Mechatronics Automation.［S.l.］：IEEE，2014：573-577.

［9］ LI Jianbo，GAO Zheng.Aerodynamical characteristics analysis of ducted fan［J］.Journal of Nanjing U-niversity of Aeronautics &Astronautics，2005，37（6）：680-684.（in Chinese）

［10］KONG Weihong，CHEN Renliang.Aerodynamic characteristics of rotor/duct/fan system in forward flight［J］.Journal of Nanjing University of Aeronautics &Astronautics，2008，40（5）：571-576.（in Chinese）

［11］ENNS D，KEVICZKY T.Dynamic inversion based flight control for autonomous RMAX helicopter［C］∥Proceedings of the 2006American Control Conference.Minneapolis，MN：IEEE，2006：8.

Mr.Chen Zhi is a Ph.D.candidate at College of Automation，Nanjing University of Aeronautics and Astronautics. He received his M.S.degree from Nanjing University of Aeronautics and Astronautics in 2011.His research interest includes sliding mode variable structure control and flight control.

Dr.Wang Daobois currently aprofessor and doctoral tutor in Nanjing University of Aeronautics and Astronautics.His research interests are UAV flight control and simulation，mechanical and electrical simulation technology，electric servo control technology.

Dr.Zhen Ziyangis currently an associate professor in Nanjing University of Aeronautics and Astronautics.His research interests are flight control，integration control，computational intelligence.

Dr.Wang Biao is currently an associate professor in Nanjing University of Aeronautics and Astronautics.His research interests are computer vision，precision guidance，flight control and simulation.

（Executive Editor：Xu Chengting）

V249.1；V275.1 Document code：A Article ID：1005-1120（2016）02-0199-09

＊Corresponding author，E-mail address：dbwangpe@nuaa.edu.cn.

How to cite this article：Chen Zhi，Wang Daobo，Zeng Ziyang，et al.Modeling and sliding mode control with boundary layer for unmanned coaxial rotor ducted fan helicopter［J］.Trans.Nanjing Univ.Aero.Astro.，2016，33（2）：199-207.

http：//dx.doi.org/10.16356/j.1005-1120.2016.02.199