Optimal Control of Reinforced Plate Based on the Minimum Energy

Liu Lu，Qiu Jinhao，Ji Hongli，Liu Canchang

1.State Key Laboratory of Mechanics and Control of Mechanical Structures，College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China2.School of Transportation and Vehicle Engineering，Shandong University of Technology，Zibo 255049，P.R.China（Received 3June 2015；revised 25September 2015；accepted 13October 2015）



Optimal Control of Reinforced Plate Based on the Minimum Energy

Liu Lu1，2，Qiu Jinhao1＊，Ji Hongli，Liu Canchang

1.State Key Laboratory of Mechanics and Control of Mechanical Structures，College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China
2.School of Transportation and Vehicle Engineering，Shandong University of Technology，Zibo 255049，P.R.China
（Received 3June 2015；revised 25September 2015；accepted 13October 2015）

An optimal control method based on the minimum energy of the vibration system is proposed for piezoelectric damping control of the reinforced aircraft plate.Subsequently，the dynamic equations of the piezoelectric damping reinforced plate system and the state space equations are derived.The method to determine the weight matrix of the system is presented based on the minimum energy of the vibration system.In order to obtain the optimal controller，the control parameters of the feedback controller are obtained by using the optimal method.A piezoelectric vibration optimal control experiment platform is designed to control the vibration of reinforced aircraft plate. The experimental results show that the method has good control performances.

vibration damping；optimal control；piezoelectric；linear vibration control

0 Introduction

As for the vibration control of flexible structures，the researches on the active control techniques have been widely concerned because its control effect hardly depends on external interference.The active control techniques based on the piezoelectric elements use the positive-inverse piezoelectric effect of the piezoelectric elements，so the vibration of structures is controlled by designing an external controller and applying the control voltage to piezoelectric pieces.Recent years，the vibration control of flexible structure using piezoelectric materials has become a hot topic in the field of structural vibration［1-4］.

In order to improve control performance，the optimal control method has been extensively investigated［5］.However，determining the weight matrix is a difficult problem when control force is designed by using the optimal algorithm.In previous papers，the weight matrix of optimal control is usually obtained by trial，but the heavy work and uncertainty of control can lead to some difficulties in solving the questions.Min et al.［6］determined the weight coefficient by trial and experiments in the control of intelligent boring tool. Lin et al.［7-8］proposed the necessity of the choice of weight matrix combining the minimum energy of noise and input as control target in the noise control of piezoelectric laminated structures. Wang et al.［9］put forward to the method of determining the weight coefficients through vibration damped effect and energy consumption.Chen et al.［10］advised to choose the weight coefficient matrix by experience.Angeles et al.［11］designed the weight coefficient matrix of optimal control based on values of the energy scale factor.Chang et al.［12］explored the choice method of weight matrix by taking the energy of structural vibration and control signal as a control target function.

In this paper，a method which determines the optimal control parameters of structure vibration based on energy minimum of vibration system is proposed.Furthermore，it is applied to the piezoelectric damping control of the reinforced platestructure in aircraft.The total energy function of the vibration system is taken as the target function，and the weight matrix that makes the energy of structural vibration minimal can be obtained by combining the regional optimization method. Additionally，the optimal control parameters of the feedback controller can be obtained by the optimal control algorithm.The experiment platform of optimal control is designed for piezoelectric damping，and then the reinforced plate structure of aircraft is studied by experiment.The experimental results show that the control method has good control performances.

1　Electromechanical Model of All-Clamped Reinforced Plate Embedded Piezoelectric Elements

In this paper，the vibration control problem is studied for the all-clamped reinforced plate stuck with the piezoelectric elements，which have five piezoelectric pieces stuck on the position as shown in Fig.1.Different piezoelectric elements are acted as sensors and actuators in different control modes.The length，width and thickness of the all-clamped reinforced plate are 830mm，530 mm and 1mm，respectively.The whole plate is divided into nine parts by four long trusses.The center position is piezoelectric actuator and sensor for the first mode，then the left and the right are for the second mode.Therefore，the upper and the down pieces are for the third mode.The sizes of piezoelectric piece are 30mm×30mm×0.2 mm.As the reinforced plate is a complex continuous structure containing rib，it is more difficult to establish the mechanics model.However，the system can be simplified as a spring-mass system with only one degree of freedom near a resonances frequency.Its electromechanical model is described in Fig.2.

The piezoelectric element is used as a controller，and its energy that inputs into vibration system is small.That is to say，the vibration deflection of the system is small.The global struc-ture including piezoelectric elements can be regarded as linearly elastic.The dynamic equations of the resonance frequency at some order have been obtained［13］

Fig.1　Sketch diagram of reinforced plate

Fig.2　Electrical and mechanical model of reinforced plate structure

where q represents the rigid mass displacement，Fiithe other forces applied to the equivalent rigid mass，and Fpithe control force applied by piezoelectric elements.M，Cand Kare mass，damping and stiffness matrices of the structure，respectively.The piezoelectric element is attached to the plate surface，and thus its electro-mechanical equations as actuators and sensors can be written as

where viand Iiare the outgoing voltage and current from the piezoelectric elements，respectively.αiis the force factor，and coithe blocked capacitance of the piezoelectric elements.The parameters of the structure are described as follows

where f0i，f1iare the resonance frequencies of a certain order of the piezoelectric element at short circuit and an open circuit，respectively，εiis the damping ratio of the plate when the piezoelectric element is in open circuit，λithe proportionality coefficient of voltage to displacement in open circuit.

The governing equations of the vibration system can be obtained from Eq.（1）

where

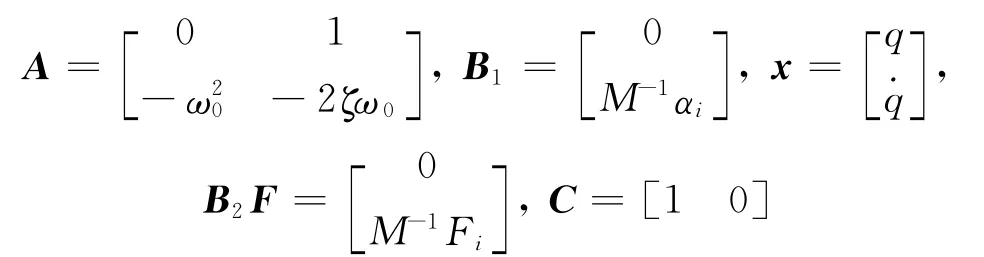
whereω0is the resonance frequency andζthe damping ratio.

2　Optimal Control Based on the Minimum Energy

Taking the mechanical energy of vibration system as the objective function，the weight matrix with the minimum energy can be obtained under constraint conditions by regional optimization.The corresponding optimal feedback control parameters can be obtained by using the optimal control algorithm.

2.1 Optimal control algorithm

In order to achieve the optimal control voltageμi，the quadratic from performance function can be expressed as［14-15］

where Jis the performance index of optimal control corresponding to state equation.Qand Rare the semi-positive-definite and positive-definite weight matrices on the outputs and inputs，re-spectively，here，αandβ are the coefficients of weight matrices；Andt0，tfthe initial time and final time，respectively.

The actuator input voltage can be written as

where Pis the positive-definite Riccati matrix of the system，which satisfies the following Riccati equation

Substituting Eq.（11）into Eq.（8），we will deduce

2.2 Determination of weight matrixes Qand R

Applying linear quadratic regulator（LQR）algorithm to the design of control force，the weight matrixes Qand Rare the two important control matrices which determine the control force and the structural reaction under the control force.It is demonstrated from Eq.（10）that the structural reaction decreases and the control force increases with Q.On the contrary，the smaller the Ris，the bigger the control force is and the smaller the structural reaction is.Since the actuate force of the vibration system is provided by piezoelectric pieces，the control force of piezoelectric materials is proportional to the voltage in linear range.In order to increase the control force，the control voltage needs to be improved.However，high voltage not only needs sufficient power supply system，but also brings a series of security issues.Therefore，voltage cannot be too high in practical applications.In previous papers，the optimal control voltage is usually obtained by trial，which can lead to heavy workload and uncertainty.In this paper，the mechanical energy of the vibration system is used as target function，and the values Qand Rof the minimum energy can be obtained under the safety voltage constraints by the regional optimization.

Eq.（14）can be written in the form of differential equations

whereδi=2ζiω0i+k2i，ω2ni=ω2

0i+k1i.The solu-tion of Eq.（15）is

The initial condition is set as follows

The vibrational energy of the system is

The conditions of the minimum energy under the constraint are

The optimal control voltage that satisfies the condition can be obtained by the regional search.

Qand R can be obtained by the following procedure：

Step 1 Set initial values of the weight matrixes Qand R.

Step 2 Calculate Kusing LQR（A，B，Q，R）.

Step 3 Calculate the mechanical energy of system using Eq.（18）.

Step 4 Get the optimal control matrix Kunder the constraint through the regional search.

3　Simulation and Experimental Verifications

3.1 Simulation analysis

In this paper，the active vibration control of the reinforced plate in aircraft is investigated. The experimental platform of the vibration control is set up，and the performance of the control algorithm is studied by experiment.The first three order′s natural frequencies are obtained using sweep frequency with the range 40—500 Hz.The first three natural frequencies measured by experiments are summarized in Table 1.At the same time，the dynamic equation parameters of the vibration system can be solved in Table 1.

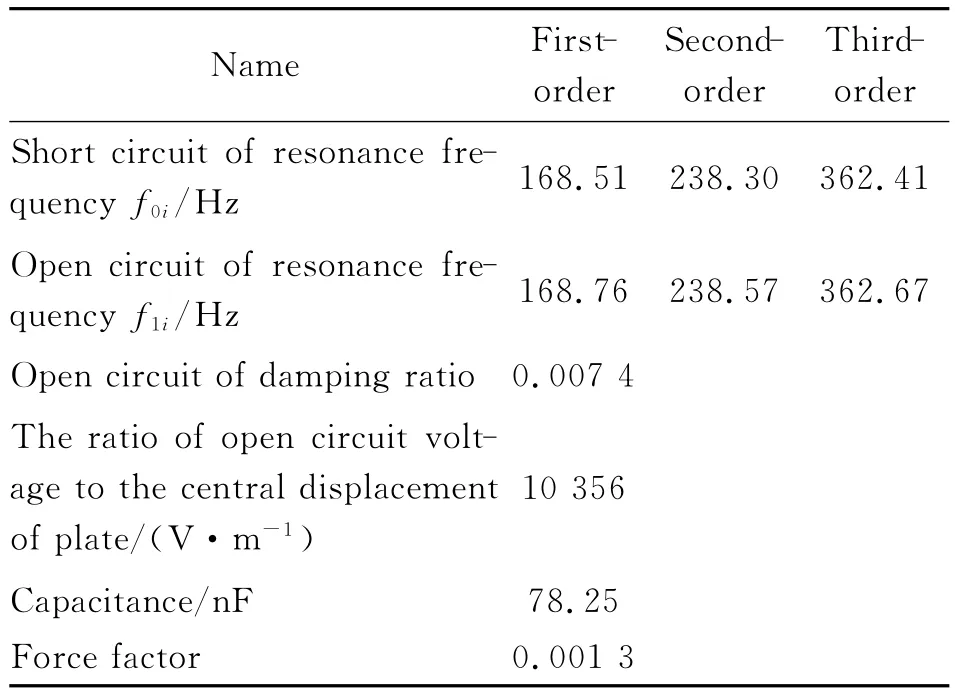
Table1　Measurement parameters of structure

The relationship between the mechanical energy of the vibration system and the weight function obtained by simulation is shown in Figs.3，4. It is showed from Fig.3（a）that the optimal weight matrix coefficientαequals 3.8whenβis equal to 2based on the minimum energy theory. Fig.3（b）clearly displays the relationship between energy and weight matrix coefficientβwhenαis equal to 3.8.It is seen from the figure that the energy is the minimum value whenβequals 2.0. In Fig.4，we demonstrates the relationship between energy of the vibration system and coefficient of weight matrix.As shown，the existing locations that correspond to the minimum energy can be determined quantitatively by adjusting the weight matrix coefficientsαandβ.

Fig.3　Relationship between energy and weight matrix coefficients

3.2 Experimental set-up

The piezoelectric sensors and actuators arebonded to the plate in the experiment.The power amplifier is HVP-300Dmade in the company of Nanjing Foneng.The vibration signal of piezoelectric sensors by the dSPACE1103board is sent into optimal controller that provides the control voltage.The control voltage enlarged by the amplifier is put into the piezoelectric controller，which controls the vibration of the reinforced plate.The weight matrix coefficients can be calculated through optimal control algorithm of the minimum energy and the vibration can be controlled by experiment.For the sake of safety，the control voltage should be controlled within 120V.

Fig.4　Relationship between energy of vibration systems and weight matrix coefficientsαandβ

3.3 Experimental results

It is indicated from Figs.5—7that the vibration of the structure is efficiently suppressed using independent modal control under the experimental conditions.The displacement amplitude of the first-mode is decreased by 43.58%as shown in Fig.5.Moreover，we can see the displacement amplitude of the second-mode is decreased to 70.29%in Fig.6.In addition，the results clearly shown from Fig.7illustrate the third-mode is decreased by 58.17%.Furthermore，the displacement amplitudes of the first-mode，the secondmode，and the third-mode are deduced 4.546，10. 289and 6.605dB，respectively.Vibration acceleration amplitudes of the first three modes are obviously suppressed.

Fig.5　Comparison of displacement of vibration control for the first mode

Fig.6　Comparison of displacement of vibration control for the second mode

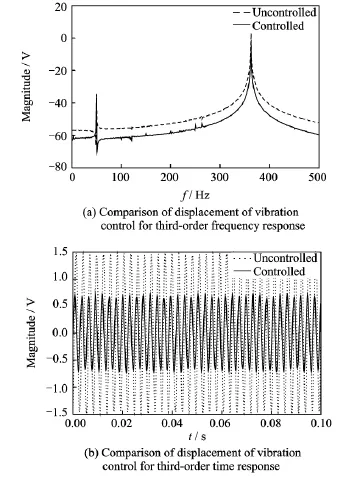
Fig.7　Comparison of displacement of vibration control for the third mode

4　Conclusions

In this paper，some conclusions are achieved as follows：

（1）An optimal control method is proposed to control the vibration of flexible structures by using piezoelectric elements.Dynamic model of piezoelectric reinforced plate is achieved，and the vibration of piezoelectric structure is controlled by the optimal control method based on the energy minimum.

（2）A method solving the weight matrix based on the minimum energy of the vibration system is advised.The weight matrix which makes structural vibration the minimum energy is obtained.The control parameters of feedback controller are obtained by using the optimal method.The vibration of piezoelectric structure is controlled.

（3）The experimental platform is set up and the experiment is carried out.The experimental results show that the control law designed in this paper has better inhibition performances on the vibration of flexible structures.The calculation work of the control law is small，so it is easy to implement.

Acknowledgements

This work was supported by the National Natural Science Foundation of China（51375228，11532006），the Fundamental Research Funds for the Central Universities（NE2015101），and the Natural Science Foundation of Jiangsu Province，China（BK20130791）.

References：

［1］ VASQUES C M A，RODRIGUES J D.Active vibration control of smart piezoelectric beams：Comparison of classical and optimal feedback control strategies［J］.Computers and Structures，2006，84：1402-1414.

［2］ SADRI A M，WRIGHT J R，WYNNE R J.LQG control design for panel flutter suppression using piezoelectric actuators［J］.Smart Mater Struct，2002，11：834-839.

［3］ HE Lili，ZHANG Jingjun，WANG Ercheng，et al. Study of active vibration control for flexible structures with piezoelectric sensors/actuators［J］.Mechanical Strength，2010，32（5）：702-706.（in Chinese）

［4］ LI S Q，QIU J H，JI H L，et al.Piezoelectric vibration control for all-clamped panel using DOB-based optimal control［J］.Mechatronics，2011，21：1213-1221.

［5］ LIU C C，JI H L，SUN H Y，et al.Optimal delayed control of nonlinear vibration resonances of single degree of freedom system［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2014，31（1）：49-55.

［6］ MIN B K，NEAL G O，KOREN Y，et al.A smart boring tool for process control［J］.Mechatronics，2002，12：1097-1114.

［7］ LIN Qirong.Mechanical behavior of piezoelectric laminated structures with application to active structural acoustic control［D］.Shanghai：Shanghai Jiao Tong University，2001.（in Chinese）

［8］ LIN Qirong，LIU Z X，WANG Q.Active control of structural acoustic pressure in a rectangular cavity using piezoelectric actuators［J］.European Journal of Mechanics-A/Solids，2001，20（4）：573-583.

［9］ WANG Zongli，LIN Qirong，LIU Zhengxing.Statedependent LQR vibration control for piezoelectric in-telligent beam［J］.Journal of Shanghai Jiao Tong U-niversity，2001，35（4）：503-508.（in Chinese）

［10］CHEN Weimin，GUAN De，LI Min，et al.Active vibration control of thin plate with piezoelectric actuators［J］.Chinese Journal of Aeronautics，2001，22（2）：109-112.（in Chinese）

［11］ANGELES K K，WANG S Y，QUEK S T.Weighted energy linear quadratic regulator vibration control of piezoelectric composite plates［J］.Smart Mater Struct，2002，11：98-106.

［12］CHANG Jun，CHEN Min，LIU Zhengxin.LOR method for multimodal active vibration control of beams based on the energy criterion［J］.Chinese Journal of Solid Mechanics，2004，25（4）：423-428.（in Chinese）

［13］JI Hongli，QIU Jinhao，ZHAO Yingchun，et al. Semi-active vibration control using piezoelectric elements［J］.Journal of Vibration Engineering，2008，21（6）：614-619.（in Chinese）

［14］OU Jinping.Structural vibration control：The active，semi-active and intelligent control［M］.Beijing：Science Press，2003：62-68.（in Chinese）

［15］LI Hongnan，LI Zhongxian，QI Kai，et al.Structural vibration and control［M］.Beijing：China Architecture &Building Press，2005：356-362.（in Chi-nese）

Ms.Liu Luis currently a lecturer of mechanics in School of Transportation and Vehicle Engineering at Shandong University of Technology.She is a Ph.D.candidate in Nanjing University of Aeronautics and Astronautics.Her research interests are vibration control and vibration isolation.

Dr.Qiu Jinhaois currently aprofessor of the smart structure in College of Aerospace Engineering at Nanjing University of Aeronautics and Astronautics.He received his Ph.D.degree in Tohoku University.His research interests are vibration control and intelligent monitors and diagnoses.

Dr.Ji Hongli is currently an associate professor of the smart structure in College of Aerospace Engineering at Nanjing University of Aeronautics and Astronautics.She received her Ph.D.degree in Nanjing University of Aeronautics and Astronautics.Her research interests are semiactive and active vibration control.

Dr.Liu Canchangis currently an associate professor of mechanics in School of Transportation and Vehicle Engineering at Shandong University of Technology.He received his Ph.D.degree in Nanjing University of Aeronautics and Astronautics.His research interests are linear and nonlinear vibration control.

（Executive Editor：Xu Chengting）

O322；O328 Document code：A Article ID：1005-1120（2016）02-0166-07

＊Corresponding author，E-mail address：qiu@nuaa.edu.cn.

How to cite this article：Liu Lu，Qiu Jinhao，Ji Hongli，et al.Optimal control of reinforced plate based on the minimum energy［J］.Trans.Nanjing Univ.Aero.Astro.，2016，33（2）：166-172.

http：//dx.doi.org/10.16356/j.1005-1120.2016.02.166