李群方法在渗流力学的应用
2016-09-13侯绍继刘曰武李奇
侯绍继,刘曰武,李奇
(中国科学院力学研究所流固耦合实验室,北京 100190)
李群方法在渗流力学的应用
侯绍继,刘曰武,李奇
(中国科学院力学研究所流固耦合实验室,北京 100190)
试图用李群方法来分析流体及渗流的运动规律.对于流形上流体、渗流力学方程的研究,物理空间的流动中的拓扑结构只要具有李群的性质,便可以此来进行流动分析.这是将李群理论直接、直地应用于渗流力学的一种方法.李群方法将众多求解特定类型的渗流微分方程方法统一到共同的概念之下.李群无穷小变换方法为寻找微分方程的闭合形式的解提供的广泛的应用,补充了求解渗流力学方程的数学物理技巧.
李群;渗流;隔开;偏微分方程;无穷小变换
1 引言
目前对于不稳定渗流问题,即是渗流中的偏微分方程初值问题和边值问题,数学上有很多方求解,如积分变换法、分离变量法、待定系数法、格林函数法.虽然这些某些解已经得到了,但是都是对一种方程有着特殊的方法不能用统一的方法去求解,本文将李群理论直接应用于渗流力学,以李群对称方法为基础,从无穷小变换准则出发,通过保持微分方程的不变性[1],导出渗流微分方程的简化方程(常微分方程(降阶)、偏微分方程(降维)),最后通过求解简化的微分系统的群不变量解,从而得出原方程的自相似解的数学描述[2].目的是为了统一和扩展形形色色的特定渗流微分方程的求解方法.
在李群方法之前求相似性解要进行细腻的物理分析找出自变量、因变量和特征物理系数的之间的无量纲组合,分析这些无量纲量之间的函数关系,通过这些组合将偏微分方程简化为常微分方程.求解依赖于对问题的物理本质有深切的了解且需要经过一些试探性的步骤.Lie提出了对称和群不变解方法,将以往的关于求解微分方程的杂乱无章的方法统一起来.
2 李群与李对称
本文所涉及的对象主要集中于定义在欧几里得空间开集上的微分方程、对称群等,为了阅读便利,本节对与之相关的基本定义、概念以及定理作简要的介绍.
经典李群框架下,李对称群由作用在自变量与未知函数空间上的几何变换构成的.目前李群理论在偏微分方程(组)中的应用主要是在以下几个方面展开的.
1.偏微分降维,即减少一个自变量,特别是含有两个自变量的方程即可化为常微分方程.
2.常微分方程降阶,对于一阶常微分方程可求出其显式解.
3.构造相似解,而这种解用其他方式很难得到.
4.生成新的解,由于对称群将方程的解变为解,因此可由一特解生成依赖于参数的新解.
2.1李群、李子群
在这一节,将对李群和李代数[3-4],李群作用和李代数作用作一个定义.并且对李群与李代数,李群作用和李代数作用的相互关系作一定的说明.
定义 1.1若已在集合G上定义了运算φ且集合满足下面公理则称为群.
封闭性:∀a,b∈G,φ(a,b)∈G
结合性:∀a,b,c∈G,φ(a,φ(b,c))=φ(φ(a,b),c)
有单位元:∃e∈G,∀a∈G,φ(a,e)=φ(e,a)=e
有逆元:∀a∈G,∃a-1∈G,φ(a,a-1)=φ(a-1,a)=e
定义1.2群G的子群:就是由G中的子集按照同样的运算规则组成的群就称为群G的子群.
定义1.3设集合G是一个微分流形,同时也是一个群,如果群的运算,即乘法运算:
乘法:

和取逆运算:

是光滑映射,那么称G是一个李群.
2.2微分方程不变性、微分方程对称群
为了处理微分方程,Lie采用扩大空间变量方法让其在一定意义下可看出比较高维空间的代数方程,Lie的微分方程延拓理论基于这个思想将代数方程的不变群理论使用到微分方程上来 [5-6].
Lie证明了偏微分方程的解可以在群变换下转换成一个不变量.对常微分方程可以降阶,偏微分方程则可以降维[7].
对于一个n阶微分方程,
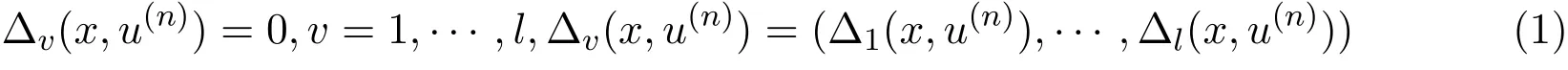
其中 x是自变量,u是因变量,x=(x1,...,xp)是自变量数目,p是因变量数目.u= (u1,...,up),q是因变量数目.
方程的解可以表示为u=f(x),或者uα=fα(x1,...,xp),其中α=1,...,q,u(k)项是指u对x的k阶偏导数,m,k,p,q都为任意正整数.
无穷小变换为:

微分方程的n阶延拓为:

令向量场为:
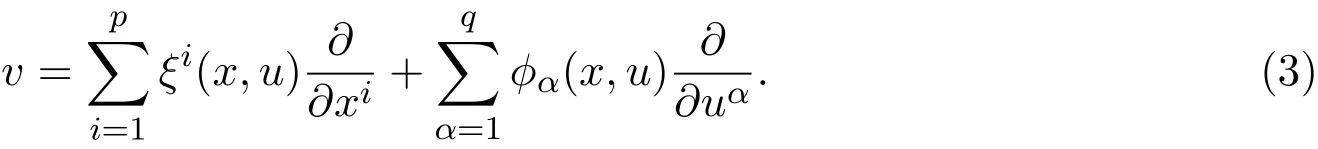
n阶延拓为:

其中:
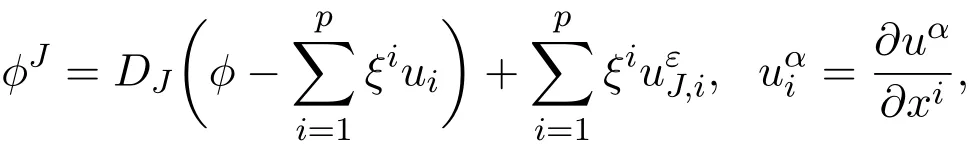

则微分方程的延拓满足:

若方程在群变换作用下保持不变,那么方程的不变量可以通过积分特征方程来得到:
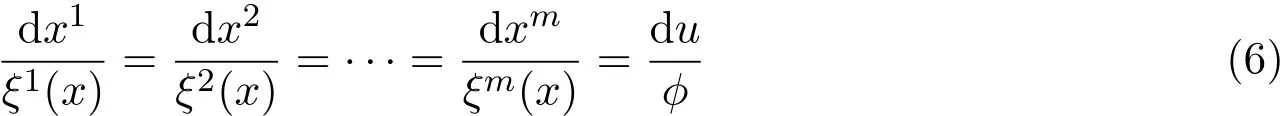
通过(5)求出ξi,φ的表达式后将其带入(6)中,求出群不变量,将群不变量带入原偏微分方程便可得到原方程的降维方程.在某些特殊情况下,很容易得到将维方程的解,从而得到原方程的自相似解.
3 不稳定渗流力学方程求解
3.1弱可压缩液体多孔介质径向流动
假设在无限大且均质油藏中有一口丼,这口井在t=0(s)时开井,并以恒定产量q(cm3/s)生产;开井前整个油藏地层压力相同,保持原始地层压力.我们有下列方程描述:

初始条件:

边界条件:

为解方程(7)引入变量的线性变换群:

将(11)代入方程(7)得到:
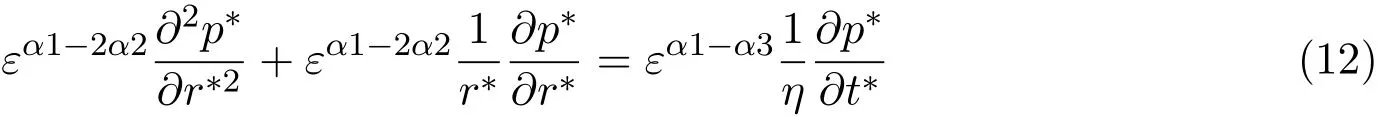
从而必须有:


a是待定量.将(14)代入方程(7)可以得到

令a=4η可以化简方程得,

定解条件化为:
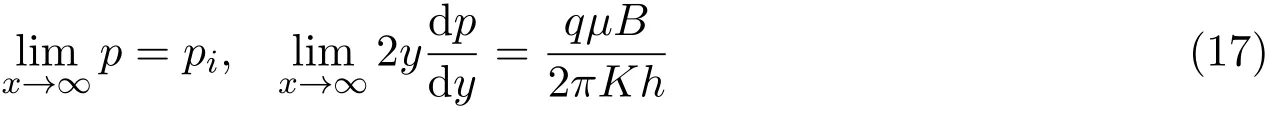
我们对于常微分方程(16)很容易解的本文略去过程,其解为:

即:

这就是弱可压缩系数液体多孔径向渗流在无限大均质油藏在压力分布公式.
至此我们用李群方法完美解决了多孔介质径向流动的PDE.
3.2无限区域弱可压缩液体多孔介质二维流动
考虑无限空间区域均质地层.原始地层压力为pi,开井前整个油藏地层压力相同,保持原始地层压力pi,求任意时刻压力分布.这是典型的扩散现象,满足的PDE方程和定解条件为:



为了解决这方程我们首先考虑p∝ρ关系,改写方程(20)为方程:


这里x=(x1,...,xn),n≥2.
由于本问题是二维问题很难用一个不变量代入求解,我们试图求方程(23)的对称无穷生成元,方程生成元有下面算子计算:
用本文2.2经典李群方法可以计算无穷小生成元:
考虑方程李群无穷小变换:

微分方程产生的向量场为:

1阶延拓为:

其中

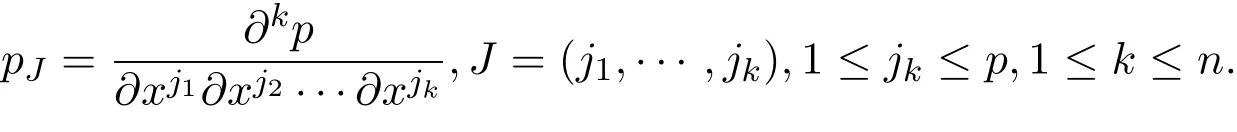
则微分方程的延拓满足

求出ξi,φ,既可以得到,


这个方程得到特征线方程:

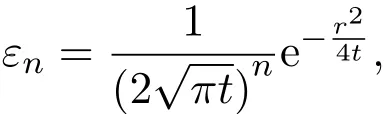
式中

现在要求方程(20)的通解,由于方程(20)为线性可以用基本解来线性组合构造通解,设通解为:

式中:b是常数.
考虑质量守恒原理:任意时刻介质中流体增量为:

将(34)代入(33)得到:

积分(35)得到:

将(36)代入(33)得到瞬时点源诱导密度 ˜ρ:

由密度和压力之间关系式:˜ρ-ρi=ρicf(˜p-pi),δm=ρiδV.则式(37)可以写为:
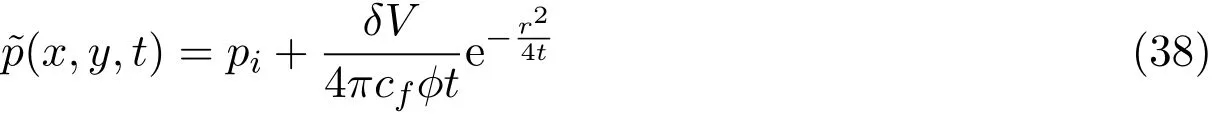
实际渗流是某一时刻开始持续一段时间进行采出或注入,作为点源是持续点源.由于方程和边界条件和初始条件都是线性,故而解可以叠加.若讨论点源在M(0,0)处,从t=0持续注入,对单位厚度地层而言地层体积流量q(t)可以写成:

则持续源的压力解为:

至此我们求出了方程(23)的持续源的解,现在来求方程(20)的解,我们只需将做坐标变换即可令t=χτ,代入解(40)得到方程(20)的解:

讨论:
对于生产井(汇),q(t)=q=const,则压力降的表达式:
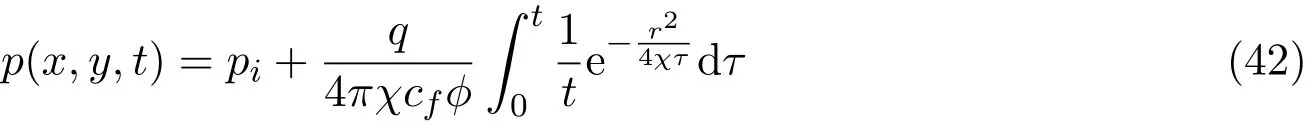
考虑地层厚度,丼产量为

则(42)式写成标准形式:

4 两相流在多孔介质的扩散
该问题是描述两相相混流体流经多孔介质在混合区域浓度的变化.浓度是时间t和位置x的函数.在混合区两侧由单一流体方程描述运动,在混合区由更加复杂流体方程描述运动,即使在一维情况下,流体的发生纵向和横向混合情况也很复杂.我们讨论关于横向流动速度随着时间的依赖在一个特定的形式
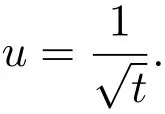
该现象产生了一个非线性的偏微分方程.这里使用李群分析将偏微分方程转化为常微分方程.许多研究人员已经讨论过这一现象从不同的方面得到其解析解为超几何函数[8].由连续性方程和达西定律可知现象满足的PDE方程:

其中c是流体A混入流体B的浓度(c含义是单位体积的质量),D是渗透率张量.考虑流体是不可压缩流体有:

当混合过程是在一维情况下,方程(44)可以化简为:

边界条件:

其中c0是初始位置浓度,cL是L处浓度.
由于u是横断面渗流速度与时间有关,它被认为是明确性为:u=,则我们将方程(46)化为:

这里为了方便我们可以假设D=1.为了解非线性方程引入变量的线性变换群G:
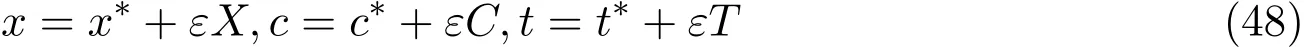
式中ε为实数.X,C,T是x,c,t的函数,将(48)带入方程(46)得到:
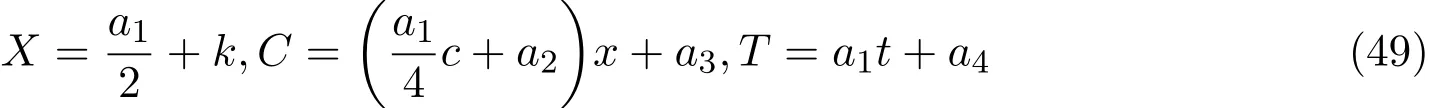
特征方程为:

设,则有a1=2,k=a2=a3=a4=0,则有

得到变换
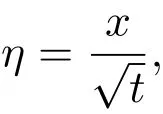
使
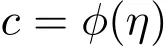
将变换代入方程(47)得到,

这是一个二阶非线性常微分方程,解这个方程得到:

erf是误差函数,c1和c2是常数,可以通过边界条件得到.通过自相似解可以发现有意义的物理扩散现象反应[9].进一步还断定纵向扩散的浓度是的符合误差函数分布.
5 结论
李群方法将求解偏微分方程自相似解方法统一到同一概念之下,是求偏微分方程自相似解简单而有效的方法,为理论求解渗流力学方程开辟新的思路,有益于找出某些问题内在对称性.李群方法可以不需要研究问题的物理方面,只要给定了偏微分方程组和定解条件就可以通过一些简单的微分和代数运算将相似性解找出来.自相似性解本质上是偏微分方程的某种对称性解,如果偏微分方程组和定解条件在某变换群作用下不变也就是说它具有某种内在的对称性,则必有这样的解.
[1]Bogfjellmo G A.The Lie group structure of the butcher group[J].Foundations of Computational Mathematics,2015,3:1-33.
[2]王珍,吉飞宇.mKdV方程的对称与群不变解[J].纯粹数学与应用数学,2011,27(6):778-780.
[3]Hamad M A A,Ferdows M.Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with a nanofluid with heat absorption/generation and suction/blowing:A Lie group analysis[J].Communications in Nonlinear Science&Numerical Simulation,2012,17(1):132-140.
[4]Carmeli C,Cassinelli G,Toigo A,et al.Unitary representations of super lie groups and applications to the classification and multiplet structure of super particles[J].nephrology dialysis transplantation,2007,8(5):viii29-viii36.
[5]MaungMin-Oo.An integrability condition for simple lie groups II[J].Department of Mathematics&Statistics,2015,27:4pp.
[6]Mei F X,Wu H B,Zhang Y F.Symmetries and conserved quantities of constrained mechanical systems[J].International Journal of Dynamics&Control,2013,2(3):1-19.
[7]刘胜,管克英.李群方法对一阶偏微分方程的应用[J].Journal of Mathematical Research with Applications,2000,20(4):545-549.
[8]李亚琼,王晓霞.由Dixon求和定理导出的超几何函数变换式[J].应用数学与计算数学学报,2015(4):431-440.
[9]Wolf J A.Stepwise square integrable representations for locally nilpotent lie groups[J].Mathematische Annalen,2014,357(357):1-17.
2010 MSC:76S05
Application of Lie Group to mechanics of fluid flow in porous media
Hou Shaoji,Liu Yuewu,Li Qi
(Key Laboratory for Mechanics in Fluid Solid Coupling Systems Chinese Academy of Sciences,Beijing100190,China)
Try to use Lie group methods to analyze the fluid and the fluid in porous media.For the fluid mechanics and fluid mechanics in porous medium research on the manifold,if topological structure of the flow of the physical space has the nature of Lie groups,we can analyze the flow.This is the theory of Lie groups directly applied to fluid mechanics.Lie group method of solving a specific type of differential equation method unified under the concept of the common.In fact,Lie group infinitesimal transformation method for the closed-form solution of ordinary differential equation with the wide application of technique,when it is applied to the partial differential equation,the method of Lie group can export symmetrical to obtain the exact solutions for partial differential equations.The mathematical physics technique for solving the equation of seepage flow is added.
Lie group,seepage,partial differential equation,infinitesimal transformation
O0357.3
A
1008-5513(2016)04-0399-10
10.3969/j.issn.1008-5513.2016.04.008
2016-03-21.
侯绍继(1992-),中国科学院力学研究所硕士,研究方向:渗流力学
刘曰武(1965-),中国科学院力学研究所研究员,研究方向:渗流力学及油气藏工程李奇(1985-),中国科学院力学研究所博士后,研究方向:油气藏工程
