仰坡坡度对隧道洞口段动力响应的影响分析①

王丽丽，吴志坚，梁庆国,孙　文,王会娟

(1.中国地震局兰州地震研究所 黄土地震工程重点实验室，甘肃 兰州 730000；2.甘肃省岩土防灾工程技术研究中心，甘肃 兰州 730000；3.兰州交通大学土木工程学院，甘肃 兰州 730070； 4.甘肃省建筑科学研究院，甘肃 兰州 730050)



仰坡坡度对隧道洞口段动力响应的影响分析①

王丽丽1,2，吴志坚1,2，梁庆国3,孙文4,王会娟1,2

(1.中国地震局兰州地震研究所 黄土地震工程重点实验室，甘肃 兰州 730000；2.甘肃省岩土防灾工程技术研究中心，甘肃 兰州 730000；3.兰州交通大学土木工程学院，甘肃 兰州 730070； 4.甘肃省建筑科学研究院，甘肃 兰州 730050)

采用动力有限元数值模拟的方法，设置四种不同仰坡坡度的模型，沿隧道轴向方向输入地震波，探究隧道洞口段及仰坡在不同仰坡坡度影响下的动力响应，并通过对无隧道通过的纯边坡模型与相同条件下有隧道通过的边坡模型的动力响应进行对比分析，研究隧道的存在对坡面动力响应的影响。研究结果表明：(1)由于临空面的存在，隧道洞口段的位移与加速度具有明显的放大效应。不同坡度模型的位移峰值皆位于y=0 m断面的拱顶处，在距洞口y=40 m后的各控制点位移差值迅速减小。(2)随着仰坡坡度的增加，同一断面处隧道的位移值随之增加，洞口段的截面变形也随之增大。(3)当坡度α≥60°时，坡面位移随着坡面高程的增加而增大；当坡度α<60°时，坡面位移随着坡面高程的增加先增大后减小，在0.4～0.6倍坡高处达到最大，即随着坡度的增加，坡面的位移峰值也就越靠近坡顶。(4)隧道的存在对于坡面的稳定性有重要影响，这种影响在洞口附近尤为明显。

黄土隧道； 洞口段； 仰坡坡度； 动力响应

0　引言

我国当前进行山区交通工程建设的过程中，桥隧结构在整条线路中所占的比例越来越高，如兰渝铁路有近70%的线路是以桥梁和隧道形式通过。仰坡坡度的大小不仅关系到施工的安全性及施工进度，而且对隧道在未来地震中的动力响应及抗震性能也具有重要影响，对整条线路的安全运营和震后快速救援与修复具有重要的控制作用。同时，山岭隧道会受到地震作用下动力放大效应的影响，且其洞口段所处的边坡一般会受到地表水侵蚀，坡面裂隙发育，因此不同坡度的仰坡稳定性对隧道的安全性具有重要影响。

已有的研究表明，国内外众多学者对隧道洞口段的动力响应[1-5]以及仰坡的稳定性分析[6-9]给与了重点关注，而对考虑仰坡坡度影响的隧道洞口段抗震理论与技术的研究较少。有关隧道洞口段抗震稳定性的影响因素方面，多将围岩的工程性质与埋深作为研究的重点[10-11]，而较少考虑到隧道的存在对仰坡稳定性的影响及影响的范围。本文采用动力有限元数值模拟的方法，通过设置不同仰坡坡角的模型，探究隧道洞口段及仰坡的动力响应，并通过对无隧道通过的纯边坡模型与相同条件下有隧道通过的边坡模型的动力响应进行对比分析，探究隧道的存在对坡面动力响应的影响，以期为山岭隧道进洞方式提供有益的理论依据。

1　模型简介

1.1模型参数

在数值计算过程中，模型参数的准确性将直接影响分析结果的准确性。本文以宝兰客专王家沟隧道为工程依托，实际取样于王家沟隧道，进行关于原状样的无侧限抗压试验、三轴压缩试验、弹性模量试验、密度试验及抗拉强度[12-13]试验等，为数值分析模型提供了可靠的材料力学参数。结合铁路隧道设计规范(TB 10003-2005)，岩体、支护结构的物理力学参数如表1所示。

表1　数值模型材料物理力学参数

1.2地震波的选取

本文所采用的地震波是MIDAS/GTS有限元分析软件中自带的1940,El Centro Site地震波,其峰值=0.356 9g，持时=53.72 s。采用SeismoSignal软件对地震波进行滤波和基线校正。校正后的地震波加速度时程曲线图如图1所示，地震波的入射方向为平行于隧道轴向方向。

图1　地震波无量纲加速度时程曲线Fig.1　Acceleration time history curve of seismic wave

1.3模型的设置

分别设置仰坡坡角α=30°、45°、60°及75°四个不同坡度的模型，坡高统一为50 m，隧道长度为100 m，最大跨径为12.5 m，隧道距边界的距离取最大跨的5倍[15]。各模型具体的网格划分如图2所示。

2　结果分析

沿隧道轴向选取二衬的10个监控断面，分别为y=0 m、10 m、20 m、30 m、40 m、50 m、60 m、70 m、80 m及90 m。各断面结果提取点见如图3(a)所示，坡面数据提取位置见图3(b)。文中各提取点的位移、加速度皆是指时程分析过程中各点的最大位移、最大加速度。

图2　数值模型网格划分图Fig.2　Meshes of numerical models

图3　分析结果提取点分布图Fig.3　Distribution map of extracted points from analysis results

2.1隧道位移响应分析

以往对山岭隧道洞口段抗震的研究中大多以隧道在坡脚处入洞为背景。本文为探究图3中各控制点间位移响应的差别，以隧道在坡脚处入洞为背景，对不同坡度模型沿隧道轴向方向各断面控制点的位移进行提取(图4)。定义最大位移差值Δmax为隧道某断面仰拱与拱顶的位移差值最大值。位移差Δmax的大小可以衡量隧道断面的变形差值，也是对结构动力响应的一种反映。

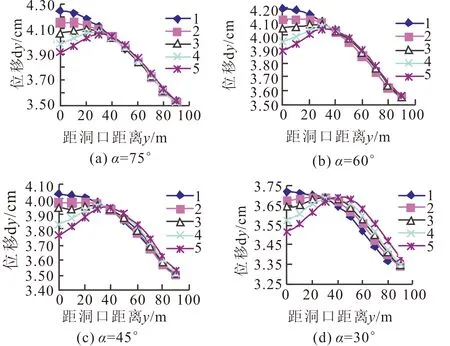
图4　不同坡度各控制点位移沿隧道轴向变化曲线Fig.4　Displacement curves of control points of different slope models along tunnel axis

分析图4知，随着断面距洞口距离的增大，1#控制点(拱顶)位移逐渐减小，在y=0 m断面处的位移值最大。而随着其他(2#、3#、4#、5#)各控制点距1#(拱顶)的距离增大，其位移随着断面距洞口距离的增大先增大后减小，在y=30～50 m间达到最大值，峰值过后位移值及各控制点间的位移差值迅速减小。

对各模型位移峰值和最大位移差Δmax进行归纳总结,如图5所示。

图5　Δmax随坡度α及控制点位移峰值的变化曲线Fig.5　Variation of Δmax with α and displacement peak values of control points

总结图5可知，不同坡度模型的隧道位移峰值皆位于拱顶处，最小值位于仰拱处；最大位移差Δmax随着仰坡坡度的增加而增大。结合图4知，最大位移差Δmax皆位于y=0 m断面。由此可知，在地震荷载作用下隧道洞口段的截面变形最大，这种变形在仰坡坡度较大时尤为明显。因此，仰坡坡度越大，洞口段在地震荷载作用下发生破坏的风险越高。

在上述对各控制点位移的变化趋势分析中发现，拱顶和仰拱的变化最具特点，因此将拱顶与仰拱位移随距离洞口距离的变化曲线进行归纳总结，如图6所示。

图6　拱顶及仰拱的位移曲线Fig.6　Displacement curves of tunnel vault and invert

由图6(a)可知，不同坡度模型拱顶的位移皆沿着隧道轴向逐渐减小，这是由于洞口临空面的存在，位移在洞口处具有放大效应。

由图6(b)知，仰拱处位移沿着隧道轴向先增大后减小，不同坡度模型的位移峰值所在的断面也不尽相同。随着坡度的增加，位移峰值出现的位置距离洞口的距离逐渐减小。结合边坡的稳定性，分析仰拱位移峰值及其出现的位置随坡角变化的原因为：边坡的安全系数随着坡角的减小而增大[16]，随着安全系数的增加，边坡的破坏模式由浅层破坏逐渐转变为深层破坏[17]，且边坡滑动面越来越缓，其上缘逐渐远离坡顶，滑体的体积逐渐增大。坡度越大，边坡的安全系数越小，滑动面也就距离坡面越近，因此位移峰值也就越靠近洞口。

综合图6(a)、(b)可知，拱顶与仰拱位移皆表现为随着仰坡坡度的增加而增大。这意味着仰坡坡度越大，洞口段的抗震设防长度也将越长。由于抗震设防段的成本远高于普通段，这将增加建设的成本。

2.2隧道加速度响应分析

将不同坡度的各模型拱顶与仰拱的加速度进行对比分析，结果如图7所示。

图7　不同坡度模型拱顶与仰拱加速度沿轴向变化曲线Fig.7　Acceleration curve of vault and invert of different slope model along tunnel axis

由图7知，拱顶与仰拱加速度沿隧道轴向的变化趋势与位移的变化趋势类似，对于不同的仰坡坡度模型，拱顶的加速度随着距洞口距离的增大而减小，仰拱加速度均呈现随着距洞口距离的增大而减小的变化形式，且不同模型同一位置的加速度均随坡度的增加而减小。这一结果验证了文献[18]的研究结果。由此可知，由于洞口临空面的存在，加速度在洞口处具有放大效应，不同的仰坡角度下均符合这一特性。

2.3坡面动力响应分析

为了探究隧道的存在对坡面动力响应的影响，设置仰坡坡度为45°与60°无隧道通过的纯边坡模型，对坡面位移和加速度随坡高的变化进行分析(图8)。

图8　不同坡度模型坡面位移沿高程变化曲线Fig.8　Surface displacement curves of different slope models along slope height

由图8(a)可知:当坡角大于60°时，坡面的位移呈现随坡高的增加而增大的趋势，在坡面最大高程y=50 m处达到峰值;当坡角小于60°时，坡面位移随着坡面高程的增加先增大后减小，在0.4～0.6倍坡高处达到最大。因此坡度的变化对坡面位移的影响可以总结为：随着坡度的增加，位移峰值也就越靠近坡顶，且随着坡度的增加，同一高程处的坡面位移也随之增大。

对比分析有隧道通过与无隧道通过的纯边坡模型坡面位移可知，当坡面高程z<10 m(即洞口处附近)时，有隧道穿过的坡面位移大于无隧道穿过的纯边坡坡面位移。在z=0 m高程处，45°坡角模型的位移差值为0.25 cm，60°坡角模型的位移差值为0.18 cm。因此隧道的存在对洞口附近的坡面位移影响较大。

图9　不同坡度模型坡面加速度沿高程变化曲线Fig.9　Surface acceleration curves of different slope models along slope height

图9为不同坡度模型坡面加速度沿坡高的变化曲线。分析图9知，不同模型坡面最大加速度随坡面高程的增加呈现先增大后减小的趋势，峰值位于1/2坡面附近。对比相同坡度的纯边坡模型与有隧道从坡底穿过的模型，前者的坡面加速度明显小于后者，且在z=0 m高程处隧道的存在对坡面加速度的影响最大。因此隧道的存在对于坡面的稳定性存在重要的影响。

3　结论与建议

(1)隧道拱顶的位移在洞口处具有明显的放大效应，位移随着距洞口距离的增加而减小；仰拱位移随着距洞口距离的增加先增大后减小，在y=30～40 m处位移达到峰值；由于洞口临空面的存在，衬砌及坡面的加速度在洞口处具有放大效应，在不同仰坡角度下均符合这一特性。

(2)随着坡度的增加，同一断面处隧道的位移值随之增加，因此洞口段的抗震设防长度将随之增大，其增大的幅度随着坡度的增大而逐渐减小。坡度越大，隧道洞口段的截面变形也就越大，在地震荷载作用下发生破坏的风险越高。

(3)坡度的变化对坡面位移有重要影响。具体表现为：当坡度α≥60°时坡面位移随着坡面高程的增加而增大；当坡度α<60°时坡面位移随着坡面高程的增加先增大后减小，在0.4～0.6倍坡高处达到最大，即随着坡度的增加，坡面的位移峰值也就越靠近坡顶。

(4)通过对比相同坡度的纯边坡模型与有隧道从坡底穿过的模型，得知隧道的存在对于坡面的稳定性有重要影响，这种影响在洞口附近尤为明显。具体表现为：无隧道穿过的纯边坡模型的洞口处坡面加速度与位移明显小于有隧道穿过的模型。

References)

[1]高峰,石玉成,严松宏,等.隧道洞口段的抗震设防长度[J].中国公路学报,2006,19(3):65-69.

GAO Feng,SHI Yu-cheng,YAN Song-hong,et al.Anti-seismic Fortified Length in Tunnel Outlet[J].China Journal of Highway and Transport,2006,19(3):65-69.(in Chinese)

[2]侯森,陶连金,赵旭,等.SH波作用下山岭隧道洞口段结构动力响应研究[J].岩石力学与工程学报,2015,34(2):340-348.

HOU Sen,TAO Lian-jin,ZHAO Xu,et al.Dynamic Response of Portal Section of Montain Tunnel under Seismic SH Wave Action[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(2):340-348.(in Chinese)

[3]闻毓民,高波,信春雷,等.基于三维离散单元法的隧道洞口段地震响应研究[J].土木工程学报,2013,46(增刊2):255-259.

WEN Yu-min,GAO Bo,XIN Chun-lei,et al.Seismic Damages Numerical Simulation of Tunnel Portal by 3-D Discrete Element Method[J].China Civil Engineering Journal,2013,46(Supp2):255-259.(in Chinese)

[4]孙铁成,王峥峥,王伟,等.双洞错距隧道洞口段地震动力响应数值模拟分析[J].北京工业大学学报,2013,39(2):220-226.

SUN Tie-cheng,WANG Zheng-zheng,WANG Wei,et al.Numerical Simulation Analyses of Seismic Dynamic Response on Portals of Two Parallel Tunnels with Staggered Space[J].Journal of Beijing University of Technoloyg,2013,39(2):220-226. (in Chinese)

[5]申玉生,高波,王英学.强震区山岭隧道洞口段结构动力特性分析[J].岩石力学与工程学报,2009,28(增刊1):3131-3136.

SHEN Yu-sheng,GAO Bo,WANG Ying-xue.Structural Dynamic Properties Analysis for Portal Part of Mountain Tunnel in Strong Earthquake Area[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(Supp1):3131-3136.(in Chinese)

[6]王帅帅,高波,周裕,等.隧道洞口含软弱夹层仰坡振动台试验研究[J].岩石力学与工程学报,2015,34(增刊1):2699-2705.

WANG Shuai-shuai,GAO Bo,ZHOU Yu,et,al.Shaking Table Test on Tunnel Front Slop with Weak Intercalation[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(Supp1):2699-2705.(in Chinese)

[7]吴冬,高波,申玉生,等.隧道仰坡地震动力响应特性振动台模型试验研究[J].岩土力学,2014,35(7):1921-1928.

WU Dong,GAO Bo,SHEN Yu-sheng,et al.Shaking Table Test Study of Seismic Dynamic Response of Tunnel Entrance Slope[J].Rock and Soil Mechanics,2014,35(7):1921-1928.(in Chinese)

[8]叶海林,郑颖人,杜修力,等.边坡动力破坏特征的振动台模型试验与数值分析[J].土木工程学报,2012,45(9):128-135.

YE Hai-lin,ZHENG Ying-ren,DU Xiu-li,et al.Shaking Table Model Test and Numerical Analysis on Dynamic Failure Characteristics of Slope[J].China Civil Engineering Journal,2012,45(9):128-135.(in Chinese)

[9]徐光兴,姚令侃,高召宁,等.边坡动力特性与动力响应的大型振动台模型试验研究[J].岩石力学与工程学报,2008,27(3):624-632.

XU Guang-xing,YAO Ling-kan,GAO Zhao-ning,et al.Large-scale Shaking Table Model Test Study on Dynamic Characteristics and Dynamic Responses of Slope[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):624-632.(in Chinese)

[10]汪成兵,朱合华.埋深对软弱隧道围岩破坏影响机制试验研究[J].岩石力学与工程学报,2010,29(12):2442-2448.

WANG Cheng-bing,ZHU He-hua.Experimental Study of Influence Mechanism of Buried Depth on Surrounding Rock Failure of Tunnel Constructed in Soft Rock[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(12):2442-2448.(in Chinese)

[11]Sharma S,Judd W R.Underground Opening Damage from Earthquakes[J].Eng Geol,1991,30(3/4):263-276.

[12]LIANG Qing-guo,WU Xu-yang,LI Chun-qing,et al.Mechanical Analysis Using the Unconfined Penetration Test on the Ten Sile Strength of Q3Loess around Lanzhou City,China[J].Engineering Geology,2014,183:342-329.

[13]吴旭阳,梁庆国,李春清,等.兰州九州重塑黄土抗拉特性研究[J].地震工程学报,2014,36(3):562-568.

WU Xu-yang,LIANG Qing-guo,LI Chun-qing,et,al.Study on Tensile Properties of Remolded Loess in Jiuzhou Development District,Lanzhou,China[J].China Earthquake Engineering Journal,2014,36(3):562-568.(in Chinese)

[14]张文涛.山岭隧道洞口段桥隧结合方式研究[D].成都：西南交通大学,2013.

ZHANG Wen-tao.Study on the Connection between Tunnel Portal and Bridges[D].Chengdu:Southwest Jiaotong University,2013.(in Chinese)

[15]李育枢,李天斌.高烈度地区山岭隧道洞口减震问题的数值模拟研究[J].公路交通科技,2009,26(10):100-104.

LI Yu-shu,LI Tian-bin.Numerical Simulation of Shock Absorption of Mountainous Tunnel Portal in Highly Seismic Region[J].Journal of Highway and Transportation Research and Development,2009,26(10):100-104. (in Chinese)

[16]王腾,谢云,孙书平.有限元强度折减法在坡度与稳定性关系研究中的应用[J].公路与汽运,2013,156(3):119-122.

WANG Teng,XIE Yun,SUN Shu-ping.The Application of Strength Compensation Method to Slope Stability and Slope Gradient[J].Highways&Automotive Applications,2013,156(3):119-122. (in Chinese)

[17]张昊,于魏伟,林杭,等.不同安全系数对应的边坡滑动面位置分析[J].岩土力学,2012,33(2):449-452.

ZHANG Hao,YU Wei-wei,LIN Hang,et,al.Analysis of Location Distribution of Slope Slip Plane with Different Factors of Safety[J].Rock and Soil Mechanics,2012,33(2):449-452. (in Chinese)

[18]陶连金,侯森,赵旭,等.不同仰坡度数的山岭隧道洞口段动力响应振动台试验研究[J].岩土力学,2014,35(增刊1):91-98.TAO Lian-jin,HOU Sen,ZHAO Xu,et,al.Large-scale Shaking Table Test for Dynamic Response in Portal Section of Mountain Tunnel with Different Gradients of Upward Slope.[J].Rock and Soil Mechanics,2014,35(Supp1):91-98. (in Chinese)

Influence of Slope Gradient on Dynamic Response in Portal Section of Tunnel

WANG Li-li1,2,WU Zhi-jian1,2,LIANG Qing-guo3,SUN Wen4,WANG Hui-juan1,2

(1.Key Laboratory of Loess Earthquake Engineering,Lanzhou Institute of Seismology,CEA,Lanzhou 730000,Gansu,China;2.Geotechnical Disaster Prevention Engineering Technology Research Center of Gansu Provence,Lanzhou 730000,Gansu,China;3.College of Civil Engineering,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,China;4.Gansu Building Research Institute,Lanzhou 730050,Gansu,China)

Using dynamic finite element numerical simulation,in this study,we establish models with different slope gradients (α=30°,45°,60°,and 75°). The incident direction of a seismic wave is along the direction of the tunnel axis. As such,we studied the influence of different slope gradients on the dynamic response of the tunnel portal section and the front slope. By setting a contrast model,a pure slope without any tunnel,we examined the influence of a tunnel on the dynamic slope response. The results show that:(1)In the presence of a free face,the displacement and acceleration of the portal section undergo an obvious amplification effect. The displacement peak values of different slope models are located in the section y=0 m (distance from the portal),and the displacement of each control point decreases rapidly 40 m from the entrance of the tunnel. (2)Along with the increase in slope gradient,the displacement value of the tunnel in the same section increases,and the deformation of the portal section also increases. (3)Whenα≥60°,with an increase in slope elevation,displacement increases; whenα<60°,with an increase in slope elevation,the displacement first increases and then decreases. The peak displacement of the slope appears at 0.4～0.6 of the slope height,which means that with an increase in slope gradient,peak displacement is closer to the top of the slope. (4)The existence of a tunnel has a significant influence on slope stability,which is particularly evident in the vicinity of the portal.

loess tunnel; portal section; slope gradient; dynamic response

2015-12-28

中国地震局地震预测研究所基本科研业务费专项(2016IESLZ04)；国家自然科学基金项目(41562013，41472297)；甘肃省基础研究创新群体资助(145RJIA332)

王丽丽(1988-)，女，山东潍坊人，硕士，研究实习员，主要从事岩土工程、地下工程等领域的科研工作。E-mail：wll_11539@163.com。

U452

A

1000-0844(2016)04-0519-06

10.3969/j.issn.1000-0844.2016.04.0519