黄土高原地震作用下黄土滑坡滑距预测方法①
2016-09-13王兰民
王 鼐,王兰民,王 谦,王 峻,王 平
(1.中国石油勘探开发研究院,北京 100080; 2.中国地震局兰州地震研究所,甘肃 兰州 730000;3.甘肃省地震局(中国地震局黄土地震工程重点实验室),甘肃 兰州 730000)
黄土高原地震作用下黄土滑坡滑距预测方法①
王鼐1,3,王兰民2,3,王谦2,3,王峻2,3,王平2,3
(1.中国石油勘探开发研究院,北京 100080; 2.中国地震局兰州地震研究所,甘肃 兰州 730000;3.甘肃省地震局(中国地震局黄土地震工程重点实验室),甘肃 兰州 730000)
为评估黄土高原地区地震滑坡致灾区域,提出一种基于模糊信息优化处理的地震滑坡滑距预测方法。在野外调查、室内试验和分析的基础上,对黄土高原的地震滑坡类型、性质和影响因素进行分析。以摩根斯坦-普莱斯法计算黄土边坡的稳定性,建立边坡最小安全系数与影响因素的关系,其影响因素主要包括地震烈度、比高、坡角、容重、内黏聚力、内摩擦角等,并在此基础上得到纯黄土地震滑坡滑距的影响关系。将黄土高原地区数次大震中采集到的93个样本数据进行归纳分析,建立模糊信息优化处理模型。所得的计算结果通过误差校验和与其他滑坡滑距预测方法进行对比,来证明本模型有较高的准确性。最后对天水市22个潜在滑坡的边坡进行滑距预测。
滑动距离; 地震滑坡; 预测; 黄土高原; 模糊信息模型
0 引言
黄土主要分布于我国华北和西北黄土高原地区。黄土高原面积辽阔,土层深厚,地貌复杂,长期受内外应力作用,形成千沟万壑,地形支离破碎。黄土高原沿断裂带地震活跃,以山西隆起、六盘山和贺兰山三个地震带的地震较频繁[1],作为地震多发区,历史上曾发生8级以上地震7次,7~7.9级地震22次,6~6.9级67次以及5~5.9级地震258次。地震造成了逾140万人次的伤亡,而地震引发的滑坡则是造成重大人员伤亡和经济损失的主要原因。根据地震资料研究,黄土高原触发滑坡产生的最小地震震级为5级。由于岩性松软,斜坡临空面大,受地震惯性力的作用易丧失抗剪强度,故每当发生较强地震时,斜坡上不稳定的土体会在瞬时抛出并埋压村庄、城市,毁坏道路、渠道,摧毁工厂、矿山,堵塞江河、湖泊,破坏农田、水库等。地震滑坡造成的损失远远大于地震本身造成的直接损失。历史上发生的众多地震引起了不计其数的黄土滑坡。据统计[2],1654年天水8.0级地震滑坡分布面积约为1 000 km2,滑距大于500 m的滑坡59个;1718年通渭7.5级地震滑坡分布面积约为3 500 km2,滑距大于500 m的滑坡337个;1920年宁夏海原地震滑坡分布面积约为50 000 km2,形成滑坡657个。本文通过收集整理甘肃省境内历史上较大的黄土地震滑坡资料,提出基于模糊信息优化处理方法的黄土地震滑坡滑距的预测方法。
滑坡滑距的预测研究目前主要有三个方向:一是基于质点运动学研究滑坡运动过程。通过上世纪90年代对随机地震荷载的深入研究,建立随机地震荷载下非饱和黄土的动本构关系,结果表明,其本构关系依然服从双曲线模型,但模型参数随所施加的随机地震荷载时程的不同而不同。并初步建立了动本构模型参数与所施加的随机地震荷载卓越周期间的定量关系[3-6]。另外坡体波动震荡效应被用来解释地震滑坡的形成,地震动使坡体波动震荡效应产生的启程剧发速度直接影响滑行速度和滑移距离[7]。Kyoji Sassa滑坡运动模型假设运动的滑坡符合牛顿流体运动方程,在此基础上可以推导出二维滑坡运动模拟微分方程。这是一种简单适用的方法[8];另一种是通过设计的振动台试验。森宽协等[9-10]提出以能量守恒法则为基础的能量法,结合土体物性参数,建立滑坡滑距预测模型。章健[11]通过分析三类滑坡的运动轨迹方程,在此基础上建立运动学模型,并根据实验及实测参数计算每类黄土滑坡的滑距,最后分析利用运动学模型计算黄土滑坡滑距方法的准确性;再一种是利用统计学原理。刘悦等[12]采用模糊信息原理用少量的滑坡数据建立模型,认为其具有普适性。随后的研究中,加入了更多的影响因素,而统计模型越来越具有针对性[13]。针对滑坡滑距的预测方法计算公式见表1。

表1 滑坡滑距预测方法
1 黄土地震滑坡分类
由于已知的滑坡分类众多,需对影响滑坡的众多因素进行分析和对比,确定一种有利于对黄土地震滑坡的特征及稳定性研究工作的分类方法,因此提出黄土地区滑坡类别。由于影响黄土地震滑坡的因素众多,在对各个因素进行分析后,通过对比各因素对滑坡影响的程度,并结合前人的研究[14-17],本文以斜坡的结构组成特点作为分类依据来对黄土地震滑坡进行研究分析。通过对147个黄土地震滑坡进行分析统计,将其主要分为四类:纯黄土滑坡、黄土-基岩接触面滑坡、黄土-基岩滑坡、黄土-砾石-基岩滑坡(表2)。

表2 黄土地区地震滑坡分类
本文主要以纯黄土滑坡为研究对象。据统计,纯黄土地震滑坡在地震滑坡中占据了极大部分。在147个滑坡中,黄土滑坡共计93个,占总滑坡数的63.3%,;黄土-基岩接触面滑坡9个,占总滑坡数的6%;黄土-基岩滑坡33个,占22.5%;黄土-砾石-基岩滑坡12个,占8.2%。
2 黄土边坡地震安全系数与影响因素
2.1边坡地震安全系数计算
黄土斜坡的地震稳定性用安全系数来定量判定[18]。本文基于极限平衡分析原理中的摩根斯坦-普莱斯方法进行计算,包括所有的条件(法向力和剪切力)同时满足力矩平衡方法和所有静力平衡方程。
静力平衡方程:
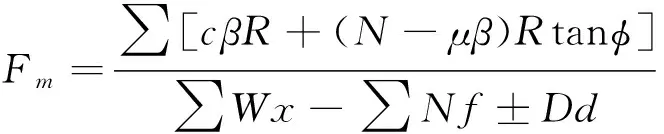
(1)
力矩平衡方程:
(2)
条块法向力方程:
(3)
迭代公式:
X=λ*f(x)*E
(4)
式中:X为条块间剪切力;E是条块间法向力;W为土体条块自重;α为底面倾角;μ是条底孔隙水压力;φ是滑面内摩擦角;c是黏聚力;滑面安全系数为F。通过式(1)~(4)计算可得不同震动加速度下的危险滑动面对应的滑面安全系数,当系数大于1时滑坡为安全,小于1时为危险(安全为S,危险为D)。将观测点所取回的试样带回实验室进行室内试验,根据《土工试验规程(SL237-1999)》对土样进行三轴剪切试验,得到c、φ值。

表3 土样对应的不同地震加速度安全系数
2.2影响因素
地震滑坡的发生、形成以及滑距受到多种影响因素的控制。这些因素包括烈度、比高、坡角、土层岩性等,是滑坡发生以及产生一定规模的充分条件。只有处于一定条件下,在地震发生时才有可能失稳产生滑坡。分析不同因素对于滑坡的影响规律,对河谷地区黄土地震滑坡的特征类型研究、数值模型建立及其稳定性分析有着重要的意义[19-20]。
(1)烈度对地震滑坡的影响
烈度是衡量一个地区受地震破坏程度的量。当地震发生时,不同烈度区内地震滑坡规模及滑坡单位面积产生数目不同。通过黄土区多次地震震害结果统计,当震级大于7级时地震影响的高烈度区内则会出现成规模的滑坡和滑坡密集区(图1)。
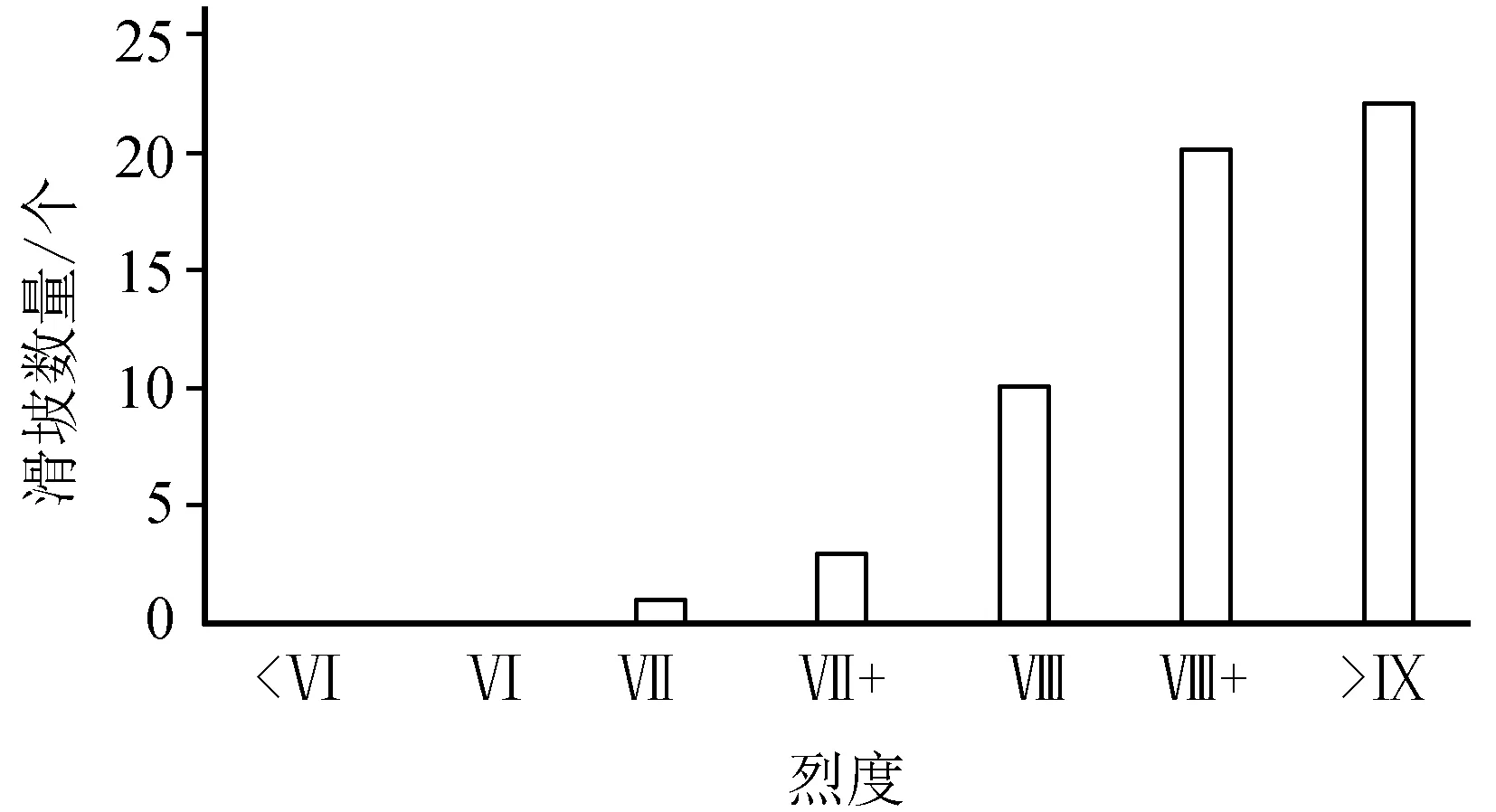
图1 不同地震烈度下滑坡产生数量分布Fig.1 Distribution of landslides under different seismic intensities
(2)坡角对地震滑坡的影响
坡角是控制滑坡发生的一个主要内在因素,是岩土稳定性的衡量指标之一,其大小反映了土体产生滑动的可能性大小。坡角决定了斜坡的形态,虽然理论上认为坡角越陡越容易发生滑坡,然而由于其他因素制衡,地震滑坡坡角主要分布于10°~25°(图2)。
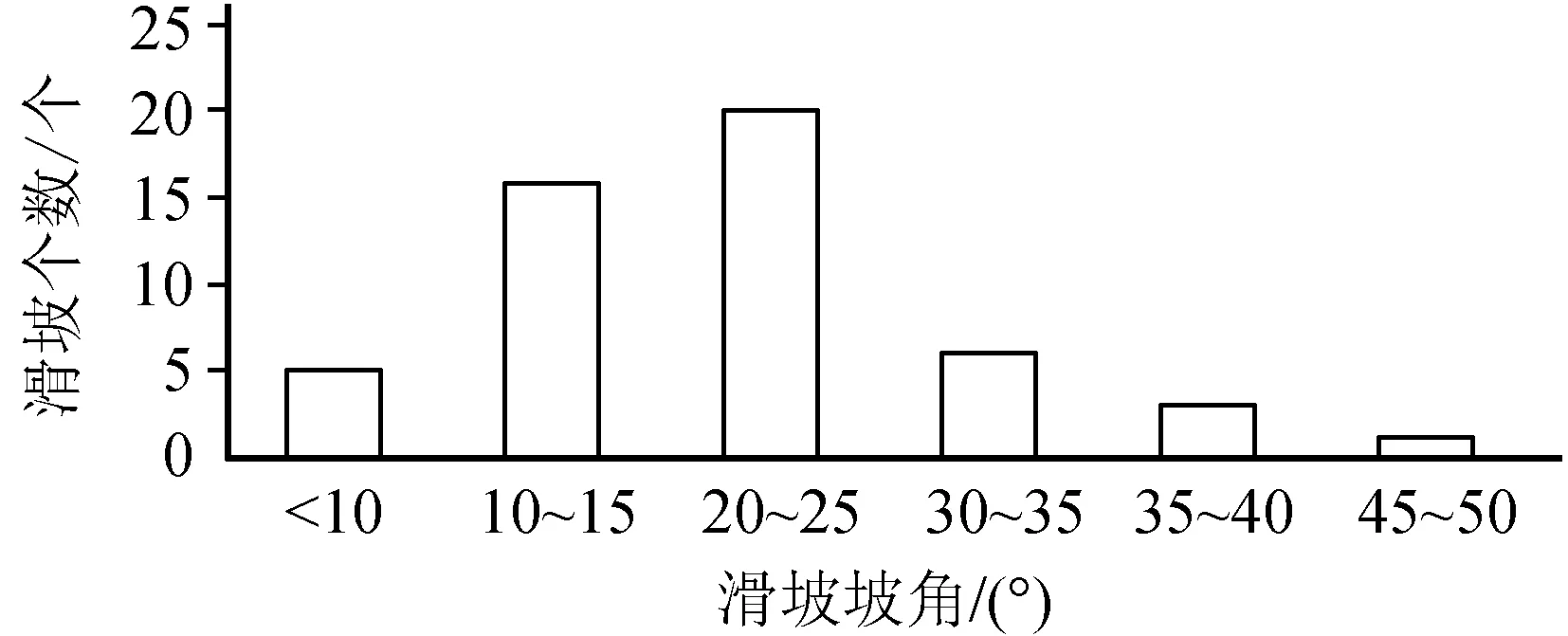
图2 不同坡角下滑坡产生数量分布Fig.2 Distribution of landslides under different slope angles
(3)比高对地震滑坡的影响
滑坡的比高体现了地表的起伏变化,反应了岩土的势能差。理论上讲,比高越大越容易发生滑坡,但统计发现地震滑坡存在一个发生频率最高的范围区间。滑坡比高主要分布于30~400 m,当比高在50~250 m时为滑坡易发区域(图3)。
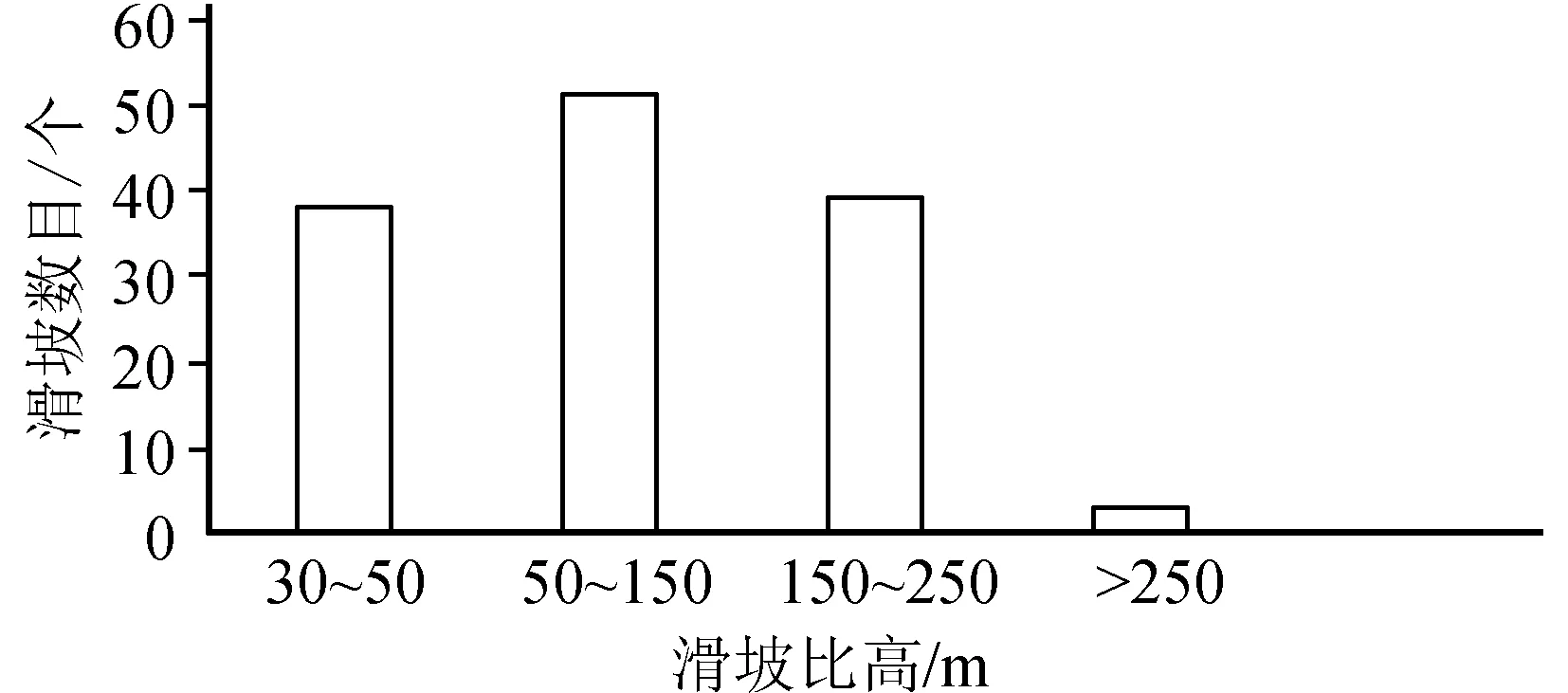
图3 不同比高下滑坡产生数量分布Fig.3 Distribution of landslides under different relative altitudes
(4)地震滑坡受土层岩性影响规律
对斜坡稳定性产生影响的黄土物理力学特性参数主要包括内黏聚力、内摩擦角与容重。选取几个典型黄土滑坡土样做数值模型,在确定两个变量的同时对第三个变量进行规律性分析,可以看出,斜坡安全系数在黄土内黏聚力与内摩擦角变化范围内呈线性上升趋势,且随黄土容重的增加而降低(图4)。
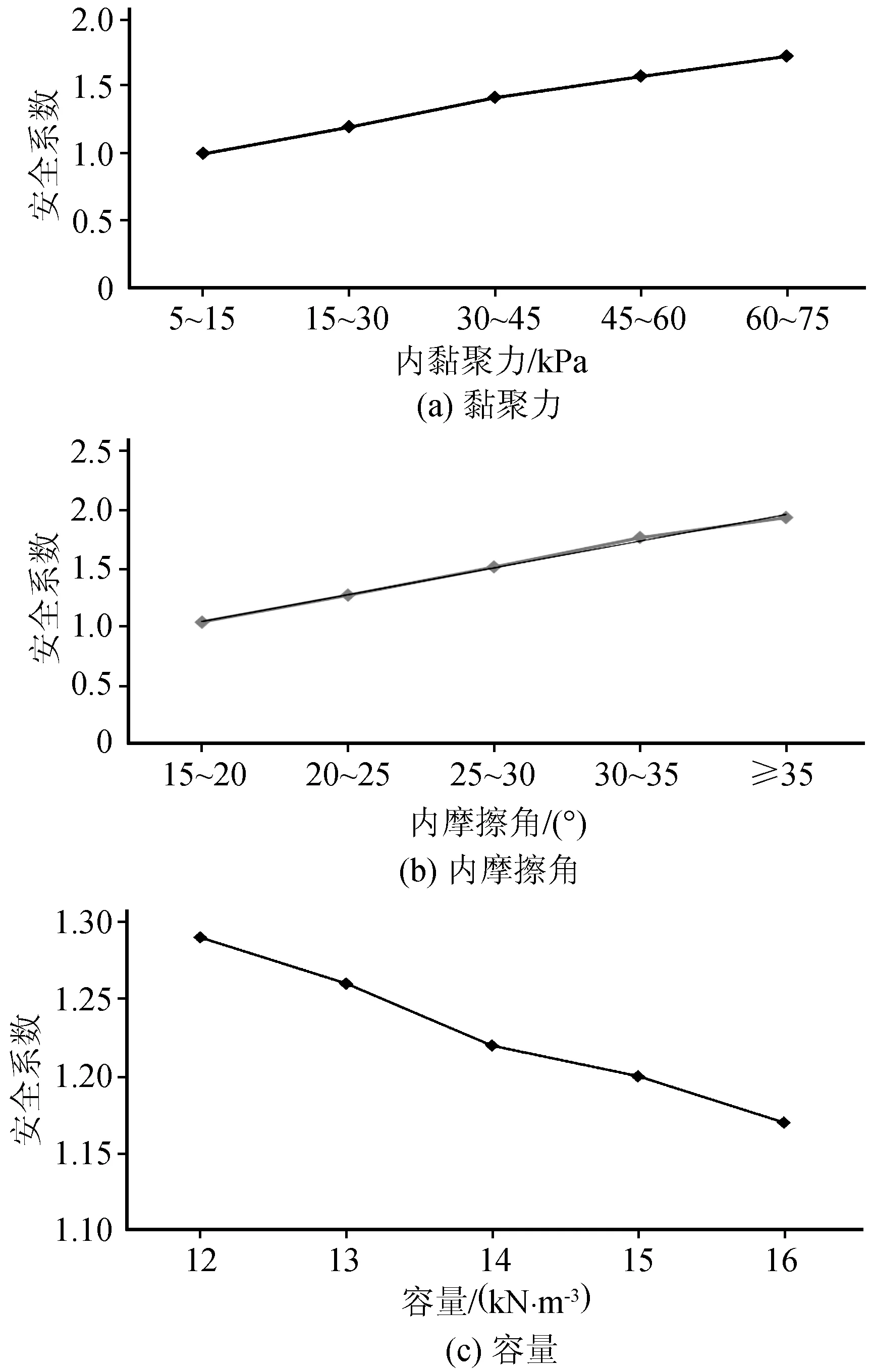
图4 不同黏聚力、内摩擦角及容重下斜坡安全系数分布Fig.4 Distribution of slope safety factor under different internal cohesions,internal friction angles and unit weights
根据图4中曲线呈现的趋势可以看出:斜坡安全系数随内摩擦角增加的上升趋势比随内黏聚力增加的趋势略微明显,即从单一因素角度分析,内摩擦角对安全系数的影响较内黏聚力影响更大。分析单一土的物性参数并不能充分研究其对斜坡安全系数的影响。对多因素进行拟合,将多个物性参数纳入计算范围才能更加准确地计算和分析河谷地区地震作用下黄土斜坡的安全系数。
3 黄土地震滑坡滑距预测方法
3.1基本原理
不同学者根据自身研究的特点提出了各自对滑坡滑距的定义。针对滑坡的致灾距离进行研究[1],将纯黄土地震滑坡滑距定义为从滑体与滑面接触的后缘至滑体滑动最远地点之间的距离。如图5所示,其中L为滑坡滑距。
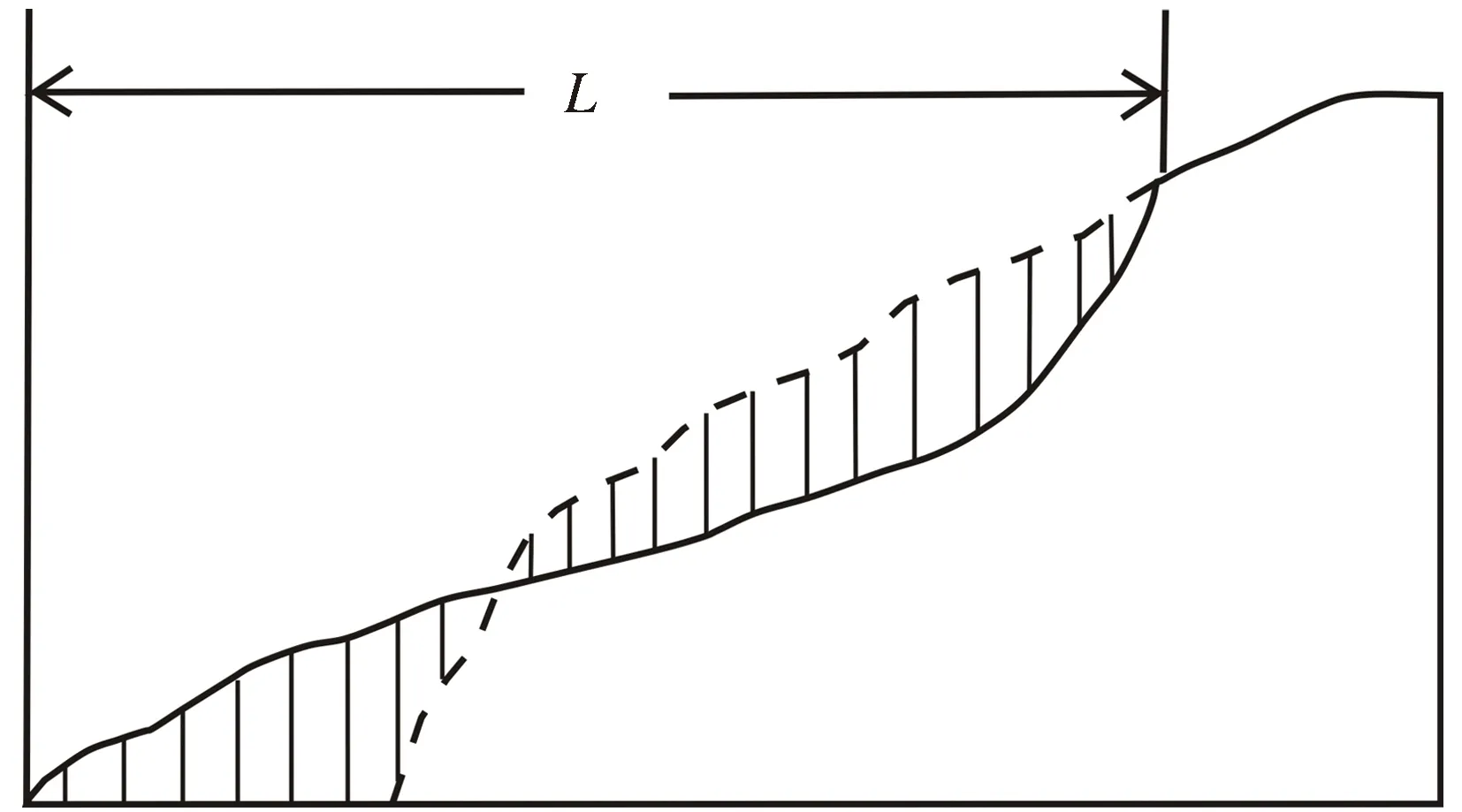
图5 黄土滑坡滑距示意图Fig.5 Sliding distance of loess landslide
模糊信息优化处理模式针对地震滑坡取样的局限性以及数据的不完整性进行优化处理,可以用来分析信息的模糊性,以便更好地帮助决策。因此,对地震作用下黄土滑坡致灾区域的研究采用模糊信息优化处理模式可以得到很好的解决。
本文拟采用的模糊信息处理方法原理如下所示:
设X是自变量论域或原因论域,Y是因变量论域或结果论域,在实用的近似推理模型中,一个论域总是由有限个离散点来表示。

(5)
令A0是一观测事件,X0是原因,Y0是结果,则A0=A0(x0,y0}。设R描述观测事件A,为刻画原因X和结果Y的因果规律,则有:
R=R(A)
(6)
因此,当已知原因X0,可以通过合适的近似推理规则“|”推出Y0。
Y0=X0|R0
(7)
3.2误差校验
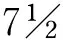
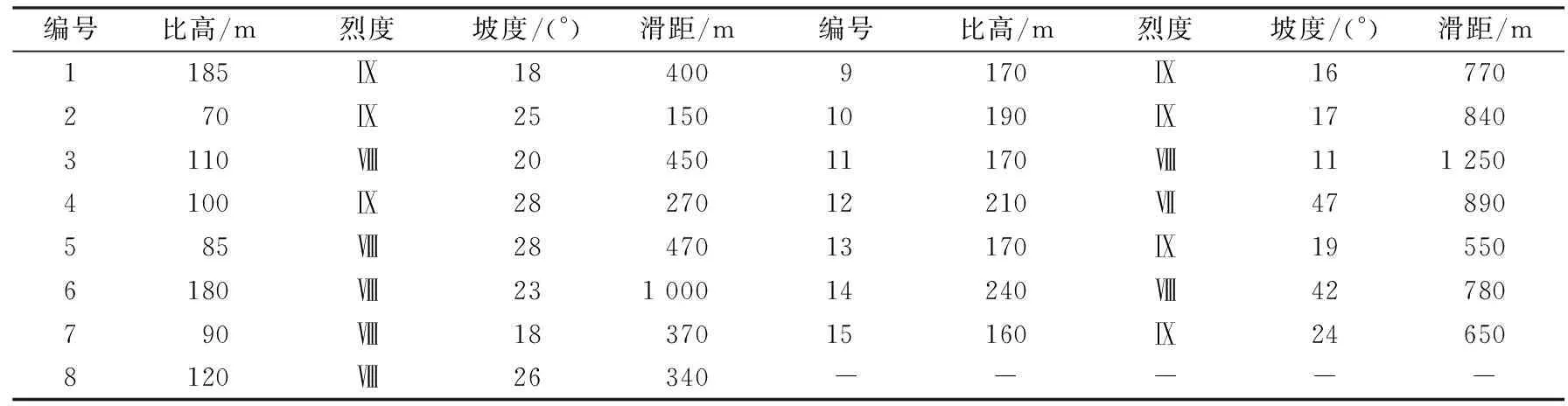
表4 通渭黄土地震滑坡参数
按照Y0=X0|R可以得到可能性分布Y0,“|”采用普通乘运算。表5为YOH利用信息集中处理求取最终结果。
同理可以算得烈度YOM和坡角YOα的滑距结果:
LH={885.2,711.3,685.3,680.6,655.8}
Lα={857.1,735.4,696.6,691.5,678.2}
LM={799.0,741.9,690.0,677.5,656.8}
通过信息集中求取最终结果如下:
L测={885.2,741.9,696.6,691.5,678.2}
L实={1250,890,550,780,650}
为验证方法的精度,将求得的最终预测滑距与实际滑距相比,求标准差:
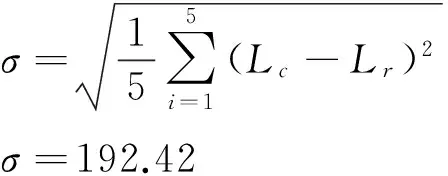
(8)
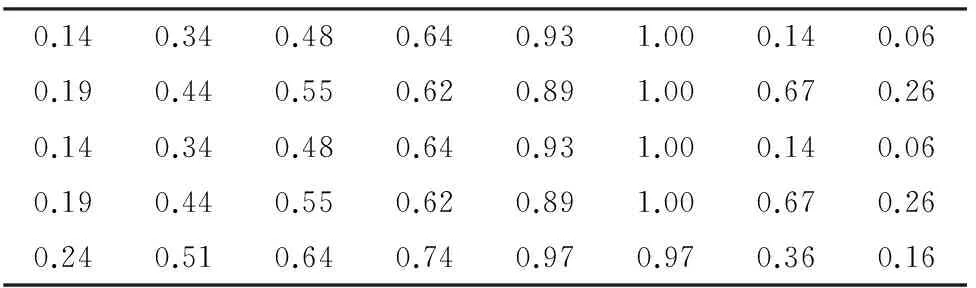
表5 模糊信息结果矩阵YOH
为进一步验本模型的可靠性,分别采用经验统计公式、舒德格尔公式和森宽协公式(表1)进行计算,并将所得结果相比较。
国内经验公式:
L={340,420,340,480,320};
σ=508.33
舒德格尔公式:
L={173.58,228.11,208.09,252.65,182.47};
σ=664.88
森宽协公式:
L={2583.08,109.46,93.86,204.43,160.88};
σ=795.94
将模糊数据优化处理模型公式预测得到的滑距与其他三种方法的结果进行对比,如图6所示。
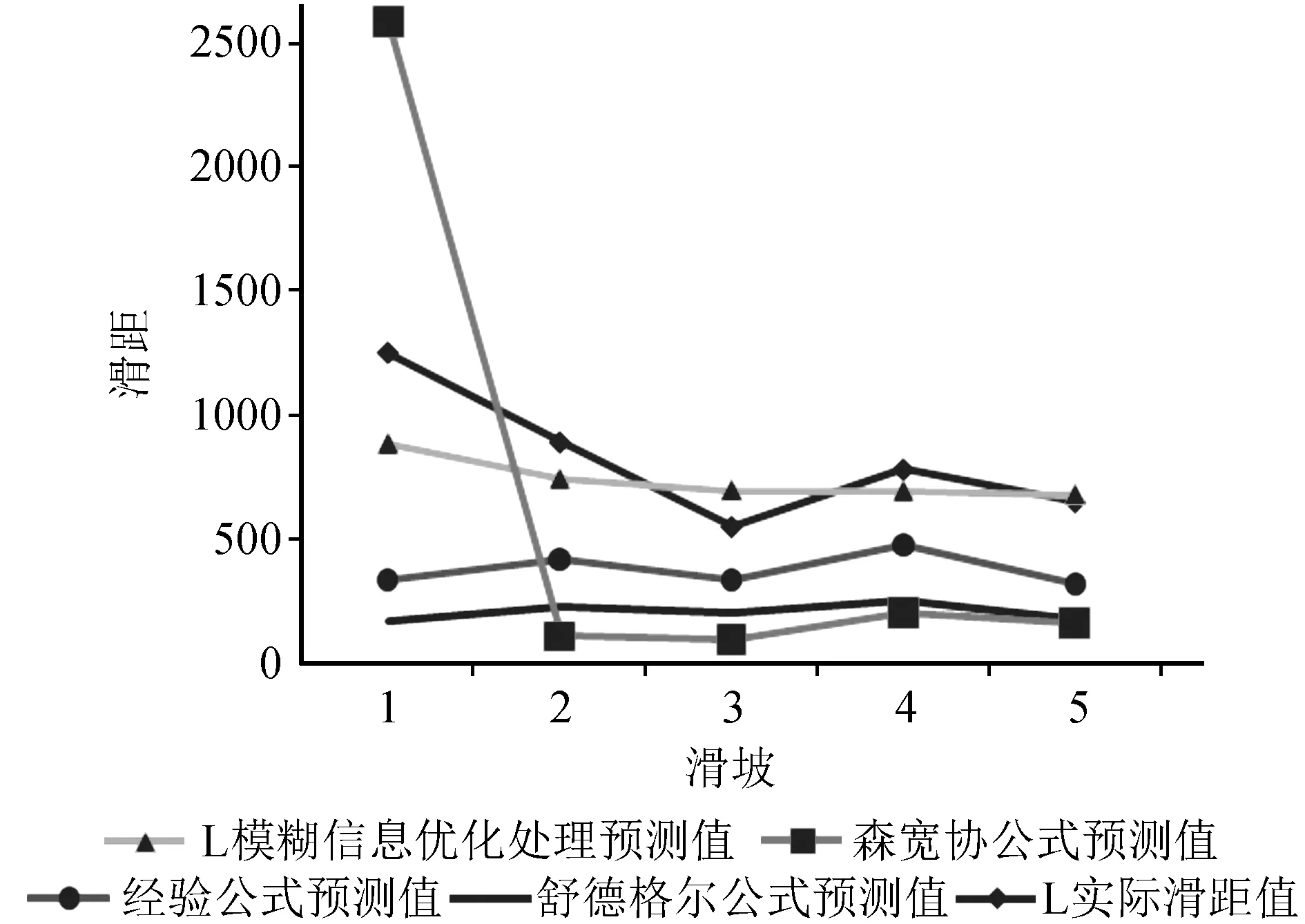
图6 不同预测方法对比图Fig.6 Comparison of different prediction methods
由图6可知,模糊信息优化处理方法对于黄土地震滑坡的滑距估算要优于其他几种方法。这是因为其他方法针对滑坡滑距的估算并没有考虑到地震的作用,而在模糊信息优化处理模型中由于加入了烈度的参数,使模型对黄土地震滑坡的预测更加准确。各方法计算结果与实际滑距的误差验算也证明了这一点。
3.3天水黄土边坡地震滑坡预测
采用模糊信息优化处理模型进行地震滑坡致灾区域预测。
通过数据分析,95%滑距L变化范围为40~1 500 m,比高H为20~240 m,平均坡角α为7°~70°,烈度M为6~9万m3。故按照模糊信息处理有关理论,依次取论域如下:
VL={L1,L2,L3,…,L8}=
{40,140,240,340,440,540,640,740,840,940,1040,1140,1240,1340,1440,1540}
μH={H1,H2,H3,…,H8}={20,40,…,220,240}
μα={α1,α2,α3,…,α7}=
{7,14,21,28,35,42,49,56,63,70}
μM={M1,M2,M3,…,M6}={6,7,7.5,8,8.5,9}
其中:VL为地震滑坡滑距论域;μH、μα、μM分别为比高论域、平均坡角论域以及烈度论域。按照二维正态信息扩散公式分别对VL和μH、VL和μα、VL和μM建立模糊关系矩阵。其中m为样本数,m=93。通过二维正态信息扩散公式分别得到原始信息分布矩阵QHL、QαL和QML,如下可见:


(9)[12]
将原始信息分布矩阵正规化处理可得各元素与滑距之间的模糊信息矩阵RHL、RαL和RML,由于篇幅有限,本文仅以烈度M为例(表6)。
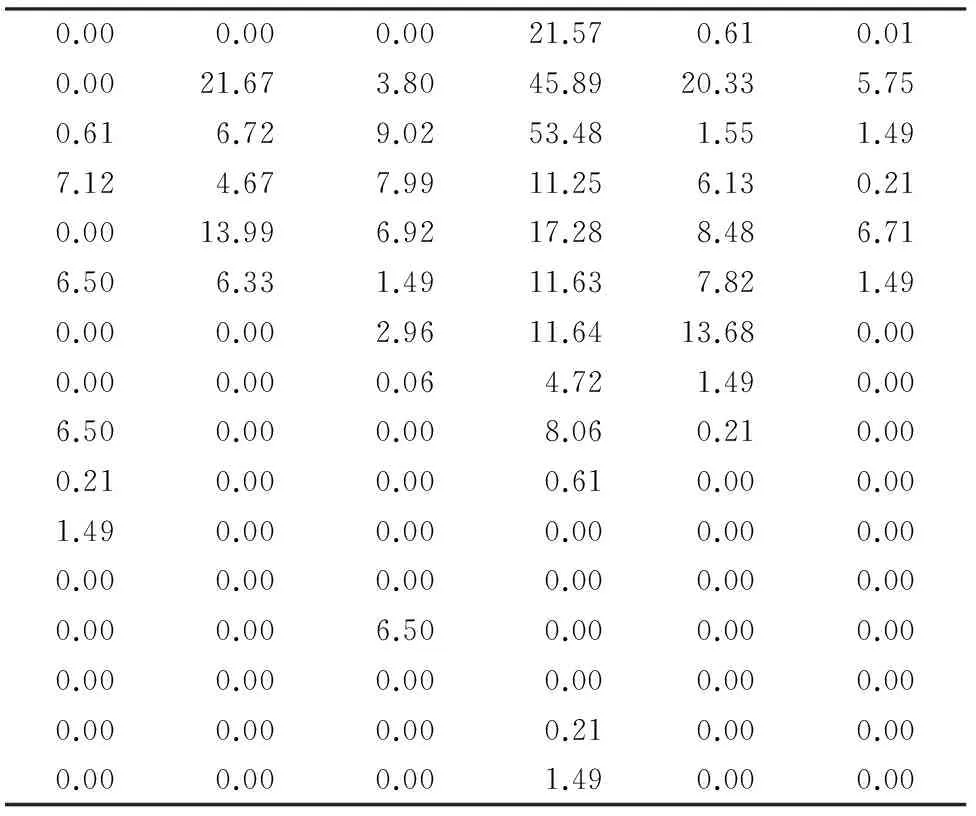
表6 原始信息矩阵XOM
将原始信息分布矩阵正规化处理可得烈度与滑距之间的模糊信息矩阵RML(表7)。
根据模糊近似推理公式Y=X|R,得到天水市22个滑坡滑距烈度的可能性分布:
{0.03,1.00,0.08,0.30,0.42,0.38,0.67,0.07,0.01,0.00,0.00,0.00,0.00,0.00,0.00,0.00}
根据信息集中公式求取最终结果:
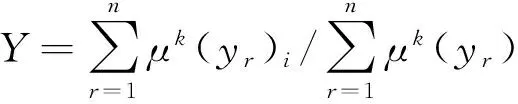
(11)
可以求得滑坡滑距如表8所列。
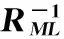
表7 模糊信息矩阵
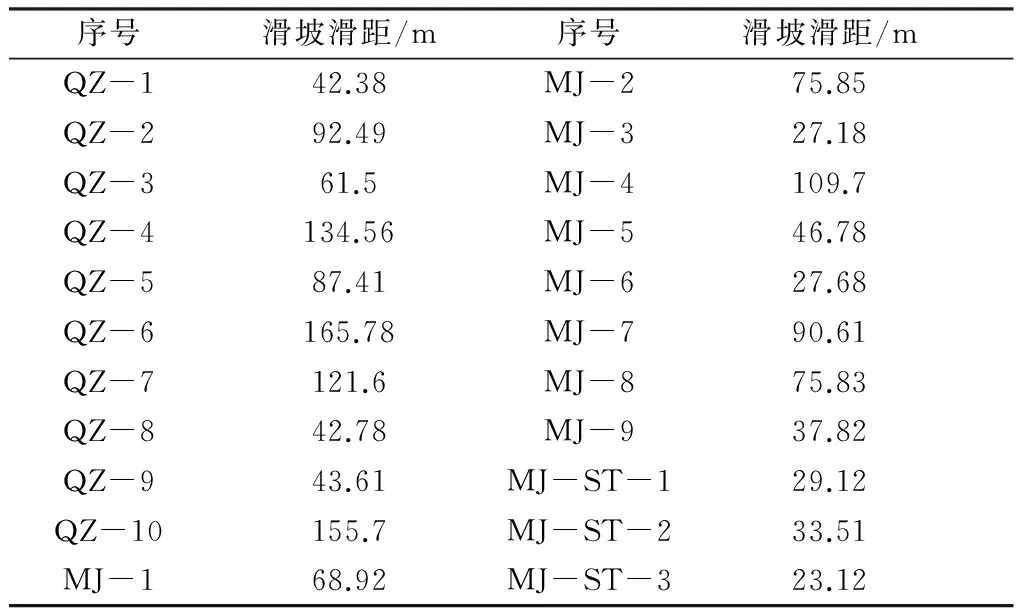
表8 天水危险性边坡滑距预测
分析结果可知,天水市区所测斜坡在地震作用下,当地震烈度大于Ⅷ度强时会发生滑坡,滑动距离从20~150 m不等。值得注意的是低速缓动的斜坡,滑距计算结果反而相对其他滑坡滑距较大,这也符合了低角度滑坡滑速缓、滑距远、致灾区域大的特点。
4 结论与建议
4.1结论
本文观测的147个黄土滑坡中纯黄土层滑坡共计93个,占总滑坡数的63.3%。采用模糊信息优化处理方法对这类滑坡进行地震诱发致灾距离预测研究,得出以下结论:
(1)通过对滑坡的特性研究,将滑坡类型分为纯黄土层滑坡、黄土-基岩接触面滑坡、黄土-基岩滑坡和黄土-砾石-基岩滑坡。
(2)采用摩根斯坦-普莱斯法进行斜坡的地震稳定性计算。通过对纯黄土地震滑坡滑距的不同影响因素进行分析,发现影响斜坡稳定性和滑坡滑距的主要因素为烈度、坡角、比高等。
(3)通过对比模糊信息优化处理方法计算结果和其他方法结果,以计算误差为量化数据,证明该方法具有较高的准确性。
4.2建议
随着对地震滑坡的深入研究,数字化和定量化在研究过程中占据了越来越重要的地位。因此,建立地震信息数据库和滑坡信息数据库,将二者科学地联合在一起并及时地共享数据,对于黄土地区地震滑坡的预防和监测具有十分重要的意义。
References)
[1]王兰民.黄土动力学[M].北京:地震出版社,2003.
WANG Lan-min.Loess Dynamics[M].Beijing:Seismological Press,2003.(in Chinese)
[2]国家地震局兰州地震研究所.陕甘宁青四省(区)强地震目录[M].西安:陕西科学技术出版社,1985.
Lanzhou Institute of Seismology,SSB.Strong Earthquake Catalogue for Shaanxi,Gansu,Ningxia and Qinghai[M].Xi'an:Shaanxi Science and Technology Press,1985.(in Chinese)
[3]张振中,郑恒利,王兰民.黄土随机振动强度参数在地震滑坡分析中的应用[J].西北地震学报,1991,13(3):45-49.
ZHANG Zhen-zhong,ZHENG Heng-li,WANG Lan-min.Application of Loess Strength Parameters under Random Vibration in Analysis of Seismic Landslides[J].Northwestern Seismological Journal,1991,13(3):45-49.(in Chinese)
[4]张振中.黄土地震灾害预测[M].北京:地震出版社,1999.
ZHANG Zhen-zhong.The Prediction of Loess Earthquake Catastrophe[M].Beijing:Seismological Press,1999.(in Chinese)
[5]王兰民,张振中,王俊,等.随机地震荷载作用下黄土动本构关系的试验研究[J].西北地震学报,1992,14(4):61-68.
WANG Lan-min,ZHANG Zhen-zhong,WANG Jun,et al.Lab Study of Dynamic Constitutive Relationship of Loess under Random Seismic Loading[J].Northwestern Seismological Journal,1992,14(4):61-68.(in Chinese)
[6]王兰民,张振中.地震时黄土震陷量的估算方法[J].自然灾害学报,1993,2(3):85-94.
WANG Lan-min,ZHANG Zhen-zhong.A Method of Estimating the Quantity of Seismic Subsidence in Loess Deposits During Earthquakes[J].Journal of Natural Disasters,1993,2(3):85-94.(in Chinese)
[7]卢育霞,石玉成,陈永明,等.地震诱发黄土滑坡的滑距估测[J].西北地震学报,2006,28(3):248-251
LU Yu-xia,SHI Yu-cheng,CHEN Yong-ming,et al.Slippage Estimation of the Loess Landslide Triggered by Earthquake[J].Northwestern Seismological Journal,2006,28(3):248-251.(in Chinese)
[8]张克亮,张亚国,李同录,等.二维滑坡滑距预测[J].工程地质学报,2012,20(3):311-317.
ZHANG Ke-liang,ZHANG Ya-guo,LI Tong-lu,et al.Prediction of Landslide Travel Distance with 2-D Newton Fluid Dynamic[J].Journal of Engineering Geology,2012,20(3):311-317.(in Chinese)
[9]Kokusho T,Ishizawa T,Nishida K.Travel Distance of Failed Slopes during 2004 Chuetsu Earthquake and Its Evaluation in Terms of Energy[J].Soil Dynamics and Earthquake Engineering,2009,29(7):1159-1169.
[10]Kokusho T,ASCE M,Ishizawa T.Energy Approach to Earthquake-induced Slope Failures and Its Implications[J].Journal of Geotechnical and Geoenviromental Engineering,2007,133(7):828-840.
[11]章健.黄土滑坡运动模式及滑距预测方法研究[D].西安:长安大学,2008.
ZHANG Jian.Study on Kinematical Model and Sliding Distance Forcasting of Loess Landslides[D].Xi’an:Chang’an University,2008.(in Chinese)
[12]刘悦,黄强兵.一种黄土滑坡滑距预测模型[J].灾害学,2001,16(3):6-11.
LIU Yue,HUANG Qiang-bing.A Forecast Pattern of the Side Distance of Loess Landslides[J].Journal of Catastrophology,2001,16(3):6-11.(in Chinese)
[13]王念秦,张倬元,王家鼎.一种典型黄土滑坡的滑距预测方法[J].西北大学学报:自然科学版,2003,33(1):111-114.
WANG Nian-qin,ZHANG Zhuo-yuan,WANG Jia-ding.A Forecasting Method of Sliding Distance on Typical Loess Landslides[J].Journal of Northwest University:Natural Science Edition,2003,33(1):111-114.(in Chinese)
[14]WANG Nai,WANG Lan-min,YUAN Zhong-xia.Characteristic and Stability Analysis for Loess Seismic Landslide in Valley City[J].Applied Mechanics and Materials,2012:1856-1863.[15]吴玮江,王念秦.甘肃滑坡灾害[M].兰州:兰州大学出版社,2006.
WU Wei-jiang,WANG Nian-qin.Landslide Disaster in Gansu[M].Lanzhou:Lanzhou University Press,2006.(in Chinese)
[16]陈永明,石玉成,刘红玫,等.黄土地区地震滑坡的分布特征及其影响因素分析[J].中国地震,2005,21(2):235-243 .
CHEN Yong-min,SHI Yu-cheng,LIU Hong-mei,et al.Distribution Characteristics and Influencing Factors Analysis of Seismic Loess Landslides[J].Earthquake Research in China,2005,21(2):235-243.(in Chinese)
[17]陈永明,石玉成.中国西北黄土地区地震滑坡基本特征[J].地震研究,2006,29(3):276-280.
CHEN Yong-min,SHI Yu-cheng.Basic Characteristics of Seismic Landslides in Loess Area of Northwest China[J].Journal of Seismological Research,2006,29(3):276-280.(in Chinese)
[18]车爱兰,吴志坚,彭东,等.黄土斜坡震害面波勘探调查及其动力稳定性分析——以甘肃岷县、漳县MS6.6地震为例[J].地震工程学报,2013,35(4):724-729.
CHE Ai-lan,WU Zhi-jian,PENG Dong,et al.Surface Wave Investigation and Dynamic Stability Analysis for Earthquake-Induced Loess Landslides[J].China Earthquake Engineering Journal,2013,35(4):724-729.(in Chinese)
[19]王鼐,王兰民.河谷地区黄土地震滑坡特征与影响因素分析[J].岩土工程学报,2013,35(增刊1):434-438.
WANG Nai,WANG Lan-min.Characteristic and Influencing Factors Analysis of Seismic Loess Slope in the Valley Area[J].Chinese Journal of Geotechnical Engineering,2013,35(Supp 1):434-438.(in Chinese)
[20]滕光亮,陈永明,石玉成,等.地震作用下节理岩质边坡稳定性影响因素研究[J].地震工程学报,2013,35(1):119-125.
TENG Guang-liang,CHEN Yong-ming,SHI Yu-cheng,et al.A Study on the Influencing Factors of Joint Rock Slope Stability under Earthquake Activity[J].China Earthquake Engineering Journal,2013,35(1):119-125.(in Chinese)
Forecasting Method for Sliding Distance of Seismic Landslides on the Loess Plateau,China
WANG Nai1,WANG Lan-min2,3,WANG Qian2,3,WANG Jun2,3,WANG Ping2,3
(1.Research Institute of Petroleum Exploration & Development,Beijing 310058,China;2.Lanzhou Institute of Seismology,CEA,Lanzhou 730000,Gansu,China;3.Earthquake Administration of Gansu Province (Key Laboratory of Loess Earthquake Engineering,CEA),Lanzhou 730000,Gansu,China)
There have been many loess seismic landslides on the Loess Plateau of Northwest,China,which have seriously affected the normal agriculture,life,and local economy of the local residents due to their high frequency and the destruction that they cause.Disaster area analysis of loess seismic landslides and the sliding distance could ascertain the endanger scope and put forward suggestions for their prevention.To evaluate the influencing area of seismic landslides,a forecasting method was presented for the sliding distance of the seismic landslides on the Loess Plateau,by means of a fuzzy information model based on the data of 93 cases.Progress in the research is shown as follows:first,combining former research and components,the loess seismic landslides developed in the loess area are divided into four types:homogeneous loess landslides,loess-bedrock interface landslides,loess-gravel-bedrock landslides,and loess-bedrock landslides.Homogeneous loess landslides,which account for over 60% of the total seismic landslides,are a main focus of this paper.Second,the Morgenstern-Price method is used for calculating the stability of loess slopes.The relationship between different factors and the safe factor is discussed in the paper and the factors such as seismic intensity,relative altitude,slope angle,unit weight,internal cohesion,and internal friction angle can influence the safe factor.Third,the impact analysis of different factors on the sliding distance of loess seismic landslides is given.It can be seen that the earthquake magnitude determines the scale of landslide disaster area,and the seismic intensity affects the distribution of the landslides.Fourth,a fuzzy information model is used for the calculation of the sliding distance.By comparing with other methods,results show that the accuracy of this method is better for forecasting the disaster area.A fuzzy information matrix was established on the basis of 93 loess seismic landslides caused by South Tianshui 8.0 earthquake in 1654,Tongwei 7.5 earthquake in 1718,Haiyuan 8.5 earthquake in 1920,and Gulang 8.0 earthquake in 1927.
sliding distance; seismic landslide; prediction; the Loess Plateau; fuzzy information model
2015-06-25
国家自然基金(51478444,51408567);中国地震局兰州地震研究所基本科研业务经费项目(2016IESLZ01)
王鼐(1988-),男,在读博士生,岩土地震工程和矿产普查与勘探专业。E-mail:piaomiaolf2007@163.com。
王谦,男,甘肃临夏人,博士,助理研究员,主要从事黄土地震工程研究。E-mail:wangq0930@126.com。
TU43
A
1000-0844(2016)04-0533-08
10.3969/j.issn.1000-0844.2016.04.0533
