LiCl-KCl-CeCl3熔盐结构与热力学的分子动力学模拟

2016-09-13姜涛王宁程长明彭述明严六明

物理化学学报 2016年3期

关键词：熔盐扩散系数摩尔

　姜涛王宁　程长明　彭述明,*　严六明

(1中国工程物理研究院核物理与化学研究所，四川绵阳621999；2上海大学理学院化学系，上海200444)

LiCl-KCl-CeCl3熔盐结构与热力学的分子动力学模拟

姜涛1王宁1程长明1彭述明1,*严六明2

(1中国工程物理研究院核物理与化学研究所，四川绵阳621999；2上海大学理学院化学系，上海200444)

采用分子动力学模拟的方法，研究了LiCl-KCl-CeCl3熔盐中CeCl3的结构性质和热力学，获得了LiCl-KCl-CeCl3熔盐中密度与组成、密度与温度的关系数据；径向分布函数gCe-Cl(r)的第一个峰位置为0.259 nm，Ce3+对应的第一个配位数约为6.9；混合熔盐中计算数据与纯熔盐中数据的差异可以解释为混合熔盐中Ce3+和C l－

的相互作用比纯的CeCl3更强；LiC l-KCl熔盐中Ce3+的自扩散活化能为22.5k J∙mo l－1，从活化能的本质来说，Ce3+自扩散所需要克服的能垒要略低于U3+(25.8 kJ∙mo l－1)。当Ce3+的摩尔分数从0.005增加到0.05时，其指前因子从31.9×10－5cm2∙s－1减少到21.8×10－5cm2∙s－1；随着Ce3+摩尔分数从0.005增长到0.05，单位体积内(忽略总体积的变化)Ce3+的增加意味着其扩散阻力增加，而自扩散的能力降低，导致了指前因子的减小。

LiCl-KCl-CeCl3；结构；热力学；分子动力学；扩散系数

1　引言

基于熔盐电解的高温干法后处理技术分离乏燃料中的锕系和镧系元素具有重要的研究意义，因此锕系和镧系元素的三价离子在熔盐体系中的结构性质和热力学性质引起了越来越多的关注1－3。在高温干法后处理过程中，锕系(U、Pu)和镧系金属离子在不同电极电位下可以从LiCl-KCl、NaCl-CsCl、NaCl-KCl和NaCl-CaCl2熔盐中选择性沉积2－4。与传统的水法后处理相比，基于熔盐电解的高温干法后处理技术采用熔盐作为介质，因而具有良好的耐辐照性能，可在线处理的优势得以体现，使得世界各国竞相开展相关的研究工作。然而，适用于高温干法后处理技术研究的基础的物理化学参数是相当缺乏的，迫切地需要开展相关研究工作特别是理论计算工作。

自1970年以来，分子动力学(MD)模拟一直是研究熔盐体系结构和热力学性质的重要理论方法之一5。该方法已经被广泛应用于研究熔融UCl36,7、镧系元素卤化物8,9以及其他三价金属氯化物10的结构与性质。最近，MD模拟被应用于研究LiCl-KCl熔盐体系的热力学性质11－14和三价金属离子在LiCl-KCl熔盐体系中的热力学性质15。

上述文献中提及的大部分研究温度集中在高温区(1073－1200K)，而从干法后处理流程的技术开发和工程实施来说更加关注能耗问题，即在相对较低的温度下来进行熔盐电解处理。

目前流程技术开发中考虑的熔盐温度范围是在熔点以上120K以内，因此获得此温度区间内的熔盐体系的结构与热力学特性则非常必要。本文主要采用MD方法研究CeCl3在LiCl-KCl熔盐体系中的结构与热力学特性。

2　分子动力学计算

2.1力场模型

采用Born-Huggins-Mayer型势函数(BHM)来描述库仑相互作用、短程排斥作用和弥散吸引作用16，如式(1)所示

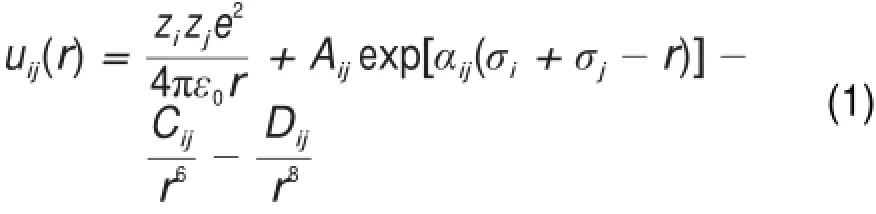
公式中zi和zj是两个相互作用离子(i,j)的名义电荷；r是两者的间距；Aij,αij,和σi是短程排斥作用的力场常数；Cij和Dij是弥散吸引作用常数。与库仑吸引作用和短程排斥作用相比，弥散吸引作用则相当弱，它对结构的计算结果几乎无影响，但会影响能量的计算结果17。虽然极化对于准确计算能量很重要，尤其是对阴离子Cl－18，但由于BHM模型在简单和准确性之间的良好平衡，该模型仍然是模拟研究熔盐体系时最被广泛接受的力场模型19。

在此模型中，将熔盐混合物近似认为是相互作用的离子，相互作用仅仅依赖于离子行为。力场常数Aij=1+zi/ni+zj/nj，其中ni是离子i的外层电子数(K+和Cl－是8；Li+是2；Ce3+是8)。σi是离子半径(σLi=0.0816nm，σK=0.1463 nm，σCl= 0.1585nm，σU=0.1430nm，σCe=0.1400nm)5,11。LiCl和KCl的αij分别为29.2和29.7 nm－1，而对于混合物则采用混合规则20进行估算。弥散吸引作用常数Cij和Dij同样采用混合规则20进行估算。所有力场常数的汇总见表1所示。

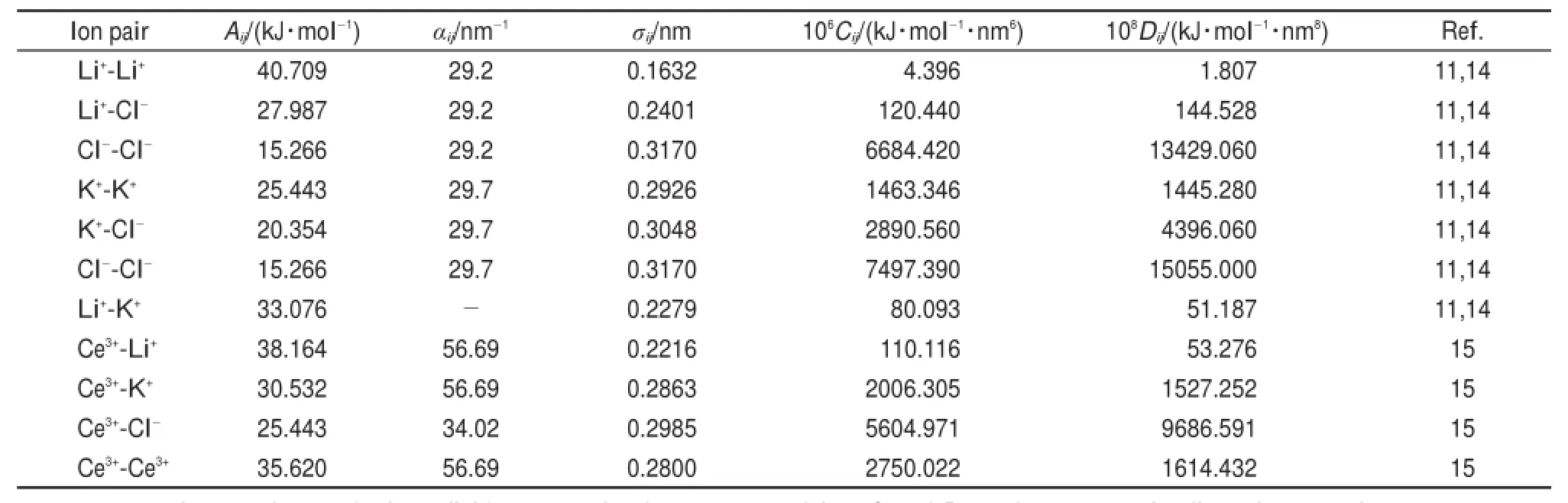
表1　力场参数汇总Tab le1 Summary of force field parameters

2.2模拟程序与方法

建立研究体系的分子力场模型后，就可以开始实施具体的MD模拟。采用通用型MD模拟程序DL_POLY21进行模拟，利用周期性边界条件，把具有无限尺度的宏观体系中的一个基本重复单元(元胞)作为实际宏观体系的近似。模拟将采用Nosé-Hoover算法实现NPT系综，压力取1.033×105Pa，温度取300K或其它设定值，温度和压强的弛豫时间皆取0.2 ps22,23；数值积分采用蛙跳算法，积分时间步长取1 fs20。静电势计算采用Ewald算法，截断半径取1.50nm；van derWaals相互作用的截断半径取1.00nm。为了提高模拟效率，采用Verlet近邻列表算法计算原子间非键相互作用力，近邻球的半径取1.20nm。

模拟体系组成如表2所示，包括LiCl熔盐和KCl熔盐，六个LiCl-KCl熔盐体系和五个LiCl-KCl-CeCl3熔盐体系。分子式后面的数字代表体系中分子的摩尔分数。KCl-36.3接近LiCl-KCl的低共熔混合物，该混合物包含58.5%(摩尔分数)LiCl和41.5%(摩尔分数)KCl，低共熔点大约是625K24－26。

以往文献19中关于氯化物熔盐的分子动力学模拟往往都是在1200K等高温下进行，而本研究是针对乏燃料后处理的研究，需要考虑实际应用背景，因此需要考察能否在尽可能低的温度下来实现熔盐电解，液相线(即初晶温度点)以上120K范围内的模拟计算数据对实际应用非常重要，而这部分的数据是相当匮乏的。为此，我们对相图的液相线(即初晶温度点)及以上六个温度点(温度步长为20K)进行了模拟。

根据表2所示的组成随机插入离子来构建初始的模拟体系。MD模拟分两步进行：准备阶段和产出阶段。在准备过程中，松散的初始元胞逐渐收缩达到平衡。确立平衡构型后，还需要执行另外1×106步的计算，作为模拟体系结构和传输特性的产出过程。

3　结果与讨论

3.1熔盐体系结构快照

图1显示KCl-50、Ce-5三种熔盐体系的结构快照。从中可以发现，所有的离子独立、均匀地分布在熔盐体系之中。

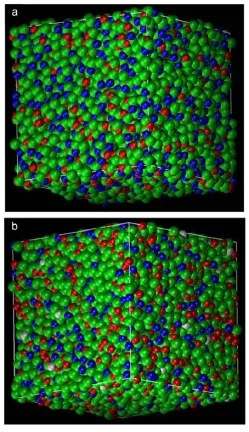
图1　在液相线温度、1.013×105Pa下模拟熔盐体系的结构快照Fig.1 Snapshotsof themolten saltm ixturessimulated at liquidus temperatureand 1.013×105Pa (a)KCl-50;(b)Ce-5.green:Cl－,red:Li+,blue:K+, white:Ce3+,color onw eb version

3.2径向分布函数

3.2.1LiCl-KCl熔盐体系

在统计力学中，粒子系统(原子、分子、胶体、……)中，径向分布函数(RDF，也称为对关联函数)g(r)为相距参考粒子r处粒子的密度。对于均匀和各项同性体系，设参考粒子处于原点O，平均粒子数密度为ρ=N/V，距离原点O为r处局域时间平均密度为ρg(r)。径向分布函数既可以用来研究物质的有序性，也可以用来描述电子的相关性。当径向分布函数用g(r,rʹ)表示时，对于|r－rʹ|比较小的情况，g(r,rʹ)主要表征的是原子的堆积状况及各个键之间的距离。对于长程的性质，由于对于给定的距离找到原子的几率基本上相同，所以g(r,rʹ)随着|r－rʹ|的增大而变得平缓，最后趋向于恒值。通常定义g(r,rʹ)时，归一化的条件为|r－rʹ|趋向于无穷大时，g(r,rʹ)趋向于1。通常，对于晶体，由于其有序的结构，径向分布函数有长程的峰，而对于非晶物质，则径向分布函数一般只有短程的峰16。

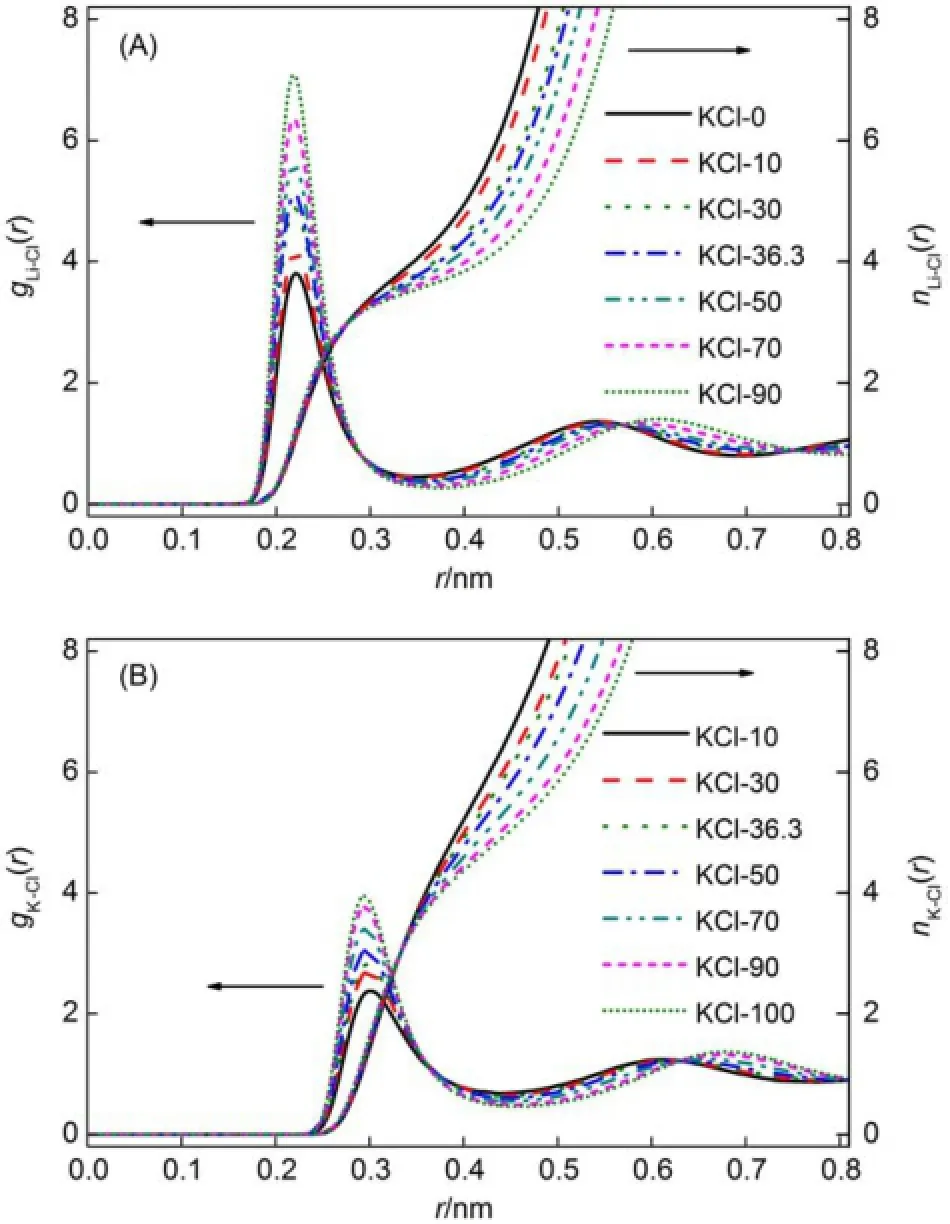
图2　不同组成的L iC l-KCl熔盐体系的径向分布函数Fig.2 Radialdistribution functions(RDF)of themolten LiCl-KClm ixturesat different compositions color onweb version

表3　熔盐体系第一个峰位置(rp)和配位数(CN)Tab le3 First peak positions(rp)and coordination numbers(CN)of themolten saltm ixtures

图2显示了不同组成LiCl-KCl熔盐体系径向分布函数(RDFs)。所有混合熔盐体系中gLi-Cl(r)和gK-Cl(r)的第一个峰位置rp并没有发生明显的变化(对于单独的LiCl和KCl熔盐来说)，分别在0.222和0.297 nm处，这些与实验值0.212－0.221 nm和0.294－0.302 nm基本一致14。通过计算从零到RDFs的第一个极小点位置的积分可以得到第一个配位数，列于表3。随着LiCl的摩尔分数从1.0降低到0.1，Li+的第一配位数从4.01减少到3.63。另一方面，KCl的摩尔分数从1.0降低到0.1，K+的第一配位数从5.16增加到6.38。这一结果与早期类似体系的MD模拟结果接近14。BHM模型很好的将结构与动力学性质联系了起来，即在K+摩尔分数增加的条件下，Li+-Cl－之间的强相互作用会引起Li+移动性的显著降低，从而使得Li+-Cl－之间的距离明显减小。从熔盐的混合效应可以很好的解释这一点。在LiCl-KCl混合熔盐体系中库仑相互作用是占主导地位的，其非线性变化是导致体系超量内能的主要部分；这个变化影响了结构离子的排布；而且阴阳离子半径比对结构有显著影响，从而在整个浓度范围内Li+保持在约四配位，而K+则保持在约六配位。而混合体系中离子的运动一般通过两种机理进行：(1)在环绕趋向于恢复电中性离子的力场中的振荡性置换；(2)关于离子和离子氛围的集合模式。

3.2.2LiCl-KCl-CeCl3熔盐体系

图3显示了不同组成LiCl-KCl-CeCl3熔盐体系径向分布函数。所有体系中Li+和K+对应的第一个峰位置和配位数与文献27计算的LiCl-KCl-UCl3熔盐体系几乎一致。gCe-Cl(r)的第一个峰位置为0.259 nm (见表3)，比在1173 K温度下，从X射线吸收精细结构光谱(EXAFS)实验中计算的纯CeCl3熔盐的最邻近距离0.281 nm略小，而第一配位数为6.9(见表3)，略大于EXAFS实验中获得的值(6.52)28。同样的现象在之前的文献27中也有报道。这些不同可以用混合熔盐体系中Ce和Cl的相互作用比纯CeCl3熔盐的更强来解释。

图3　不同组成的LiCl-KCl-CeCl3熔盐体系的径向分布函数Fig.3 Radialdistribution functionsof themolten LiCl-KCl-CeCl3m ixturesat different compositions (A)Ce-Cl;(B)M-Cl in Ce-5molten salt.coloronweb version

3.3熔盐密度

3.3.1LiCl-KCl熔盐体系

有关LiCl-KCl熔盐密度的拟合公式，可以参考Mariani的文章29和Janz的手册26的相关数据，但这些数据颇有出入。在Mariani的文章中采用了两参数拟合公式(如表4所示)，而Janz则采用复杂的多参数公式(2)，即

一般情况下，a=1.98715，b=－5.80069×10－4，c=2.02443×10－3，d=5.31098×10－11，e= 1.21294×10－7，f=－2.16826×10－8。其中ρ代表体系的密度，单位为g∙cm－3；T代表体系的温度，单位为K；C代表体系中LiCl的摩尔分数。

LiCl-KCl熔盐体系的密度随温度的变化如图4所示。密度随温度的升高而降低，与温度具有良好的线性关系，如式(3)：

其中ρ0(g∙cm－3)和b(g∙cm－3∙K－1)是与熔盐体系组分相关的常数。

表4　单组分盐的熔盐密度26Tab le4Melt densitiesof single salts26

图4　 L iC l-KCl熔盐体系密度与温度关系图Fig.4Tem perature dependenceofdensity for L iCl-KC lm olten salt

从图中数据可以看出，对于同一组分的LiCl-KCl熔盐体系，在一定温度范围内密度与温度成反比关系；对于同一温度下，LiCl-KCl熔盐体系的密度随KCl含量的增加(从10%－100%)而增加；但是也发现在同一温度下(T=883 K)，KCl-0(即LiCl-100)的密度反而高于KCl-10，作者认为虽然表面上看有10%的LiCl替换成了KCl，而K的原子量大于LiCl，密度应该增加；但是由于K+离子半径的增加，Li-K-Cl离子之间堆积变得没有纯Li-Cl离子那样紧密，使得单位体积内的K+减少，最终引起了体系密度的降低。

表5　 LiCl-KCl熔盐体系密度对比表Table5Com parison of density for LiCl-KClmolten salt

将模拟计算得到的KCl-0和KCl-100两个密度数据和文献30报道的数据分别在各自的熔点下进行了比对(见表5)，并且以文献值作为标准计算了相对标准偏差，发现KCl-0(即LiCl-100)的数据与文献30吻合的较好(RE=4.4%，相对误差)；而KCl-100的数据也只有约2.7%的相对误差。

3.3.2LiCl-KCl-CeCl3熔盐体系

图5　 LiC l-KC l-CeCl3熔盐体系密度与组成(A)和温度(B)关系图Fig.5Densitiesof LiCl-KCl-CeCl3molten salt vs com postion(A)and tem perature(B)

图6　 LiCl-KCl熔盐体系不同温度下的自扩散系数(D)Fig.6Temperature dependenceof the self-diffusion coefficien ts(D)of the LiC l-KC lmolten salt (A)Li+,(B)K+,(C)Cl－,color onweb version

同样因为铈原子比其他原子重，所以熔盐体系的密度随着CeCl3的加入而增加，在LiCl-KCl-CeCl3熔盐体系中，密度与温度、组成的变化关系如图5所示。

表6　 LiCl-KCl熔盐体系中离子扩散活化能(Ea)和指前因子(D0)Tab le 6Diffusion activation energy(Ea)and preexpontential factors(D0)of all ions in the LiCl-KClmolten salts

表7　 LiCl-KCl-CeCl3熔盐体系中Ce3+离子自扩散系数Tab le7 Self-diffusion coefficientsof Ce3+in the m olten LiCl-KC l-CeC l3m ixtures

3.4自扩散系数

3.4.1LiCl-KCl熔盐体系

图7　 LiCl-KCl熔盐体系不同温度下的自扩散系数Fig.7 Temperature dependenceof the self-diffusion coefficients in the LiCl-KCl-UCl3molten salt (A)Li+;(B)K+;(C)Cl－;(D)Ce3+

根据爱因斯坦公式，自扩散系数可以通过MD模拟得到的离子平均均方位移来计算16。从自扩散系数随温度的变化曲线(图6)可以看出，离子的自扩散系数遵循一个活化过程，遵循阿伦尼乌斯方程(见式(5))，

式中D为自扩散系数(cm2∙s－1)，D0为指前因子(cm2∙s－1)，Ea是活化能(J∙mol－1)，R是气体常数(J∙mol－1∙K－1)。D0(指前因子)是一个只由反应本性决定而与反应温度及体系中物质浓度无关的常数，与D(自扩散系数)具有相同的量纲。D0是反应的重要动力学参数之一。对于熔盐体系中离子的自扩散过程，则主要是克服离子之间的相互作用。

表8　 LiCl-KCl-CeCl3熔盐体系中离子自扩散活化能和指前因子Table8 Self-diffusion activation energiesand preexponential factors in the LiCl-KCl-CeCl3molten salts

表6总结了LiCl-KCl熔盐体系中离子自扩散系数的指前因子和活化能。K+、Li+和Cl－的活化能几乎都在24kJ∙mol－1，而指前因子依据离子和混合体系的不同而变化。由于Li+比K+小，所以Li+和Cl－之间的相互作用能比K+和Cl－的要大，K+的指前因子比Li+大，K+的自扩散系数也比Li+大(相同条件下)。然而，Cl－的指前因子总是比其他阳离子要小。

3.4.2LiCl-KCl-CeCl3熔盐体系

在LiCl-KCl-CeCl3熔盐体系中，Ce3+是一个三价阳离子，Ce3+和Cl－的相互作用比一价阳离子和Cl－的作用强，因此，我们预计Ce3+相比其他离子的自扩散系数更低。Ce3+和U3+同为三价阳离子，但是原子量不同，Ce3+的自扩散系数(见表7)比U3+大这一结果与实验值26相一致。

通过阿仑尼乌斯方程拟合自扩散系数，我们得到温度与扩散系数的关系图(如图7所示)。Ce3+的活化能是22.5kJ∙mol－1，而实验值是32.11 kJ∙mol－126，比U3+的活化能值小(25.8 kJ∙mol－1)。随着Ce3+摩尔分数从0.005增长到0.05(见表8)，Ce3+的指前因子在31.9×10－5－21.8×10－5cm2∙s－1的范围内变化，是实验值(178.0×10－5cm2∙s－1)的1/526,31。分析其中原因，认为实验值是在有外加驱动力(电场等)的条件下获得扩散系数，而模拟计算得到的是在体系平衡状态下(无外加驱动力)的自扩散系数，因此数值偏小。另外，随着Ce3+摩尔分数从0.005增长到0.05，单位体积内(忽略总体积的变化)Ce3+的增加意味着其扩散阻力增加，而自扩散的能力降低，导致了指前因子的减小。

4　结论

LiCl-KCl熔盐中Ce3+的自扩散活化能为22.5kJ∙mol－1，从活化能的本质来说，Ce3+自扩散所需要克服的能垒要略低于U3+(25.8 kJ∙mol－1)；当Ce3+的摩尔分数从0.005增加到0.05时，其指前因子从31.9×10－5cm2∙s－1减少到21.8×10－5cm2∙s－1；随着Ce3+摩尔分数从0.005增长到0.05，单位体积内(忽略总体积的变化)Ce3+的增加意味着其扩散阻力增加，而自扩散的能力降低，导致了指前因子的减小。

低温混合熔盐(三组分和熔点以上120K范围内)的结构性质(径向分布函数和密度)与热力学数据(自扩散系数、指前因子和活化能)、混合效应对它们的影响等信息对了解熔盐体系的特征和指导乏燃料干法后处理研究，以及干法后处理流程的设计具有重要价值。

References

(1)Fukasawa,K.;Uehara,A.;Nagai,T.;Sato,N.;Fujii,T.; Yamana,H.J.Nucl.Mater.2012,424(1－3),17.doi:10.1016/ j.jnucmat.2012.01.009

(2)Salanne,M.;Simon,C.;Turq,P.;Madden,P.A.J.Phys. Chem.B 2008,112(4),1177.doi:10.1021/jp075299n

(3)Ghosh,S.;Reddy,B.P.;Nagarajan,K.;Kumar,K.C.H. Calphad 2014,45,11.doi:10.1016/j.calphad.2013.11.001

(4)Roy,J.J.;Grantham,L.F.;Grimmett,D.L.;Fusselman,S.P.; Krueger,C.L.;Storvick,T.S.;Inoue,T.;Sakamura,Y.; Takahashi,N.J.Electrochem.Soc.1996,143(8),2487.doi: 10.1149/1.1837035

(5)Sangster,M.J.L.;Dixon,M.Adv.Phys.1976,25(3),247.doi: 10.1080/00018737600101392

(6)Okamoto,Y.;Madden,P.A.;Minato,K.J.Nucl.Mater.2005, 344(1－3),109.doi:10.1016/j.jnucmat.2005.04.026

(7)Okamoto,Y.;Kobayashi,F.;Ogawa,T.J.Alloy.Compd.1998, 271－273,355.doi:10.1016/S0925-8388(98)00087-5

(8)Okamoto,Y.;Madden,P.A.J.Phys.Chem.Solids2005,66(2－4),448.doi:10.1016/j.jpcs.2004.06.038

(9)Okamoto,Y.;Hayashi,H.;Ogawa,T.J.Nucl.Mater.1997, 247,86.doi:10.1016/S0022-3115(97)00094-9

(10)Abramo,M.C.;Caccamo,C.Journal ofPhysics:Condensed Matter1994,6(24),4405.doi:10.1088/0953-8984/6/24/003

(11)Ribeiro,M.C.C.The Journal ofPhysical Chemistry B 2003, 107(18),4392.doi:10.1021/jp027261a

(12)Chakraborty,B.;Wang,J.;Eapen,J.Phys.Rev.E 2013,87, 052312.doi:10.1103/PhysRevE.87.052312

(13)Morgan,B.;Madden,P.A.J.Chem.Phys.2004,120(3),1402. doi:10.1063/1.1629076

(14)Lantelme,F.;Turq,P.J.Chem.Phys.1982,77(6),3177.doi: 10.1063/1.444192

(15)Okamoto,Y.;Yaita,T.;Shiwaku,H.;Suzuki,S.;Madden,P. A.;Usami,N.;Kobayashi,K.Photon Factory Activity Report 2005#23 Part B:Chemistry 2006,27B/2004G064,13.doi:pfwww.kek.jp/acr2005pdf/part_b.htm l

(16)Yan,L.M.;Zhu,S.H.Theory and Practice ofMo lecular Dynamic Simulation;Science Press:Beijing,2013.

(17)Hutchinson,F.;Wilson,M.;Madden,P.A.Mol.Phys.2001,99 (10),811.doi:10.1080/00268970010022878

(18)Salanne,M.;Madden,P.A.Mol.Phys.2011,109(19),2299. doi:10.1039/C1FD00053E

(19)Rollet,A.L.;Salanne,M.AnnualReports Section“C”(PhysicalChemistry)2011,107,88.doi:10.1039/C1PC90003J

(20)Larsen,B.;Førland,T.;Singer,K.Mol.Phys.1973,26(6), 1521.doi:10.1080/00268977300102671

(21)Sm ith,W.;Leslie,M.;Forester,T.R.Computer Code DL_Poly_2.14;CCLRC,Daresbury Laboratory:Daresbury, England;2003.

(22)Nosé,S.J.Chem.Phys.1984,81(1),511.doi:10.1063/ 1.447334

(23)Hoover,W.G.Phys.Rev.A 1985,31(3),1695.doi:10.1103/ PhysRevA.31.1695

(24)Basin,A.S.;Kaplun,A.B.;Meshalkin,A.B.;Uvarov,N.F. Russ.J.Inorg.Chem.2008,53(9),1509.doi:10.1134/ S003602360809026X

(25)Van Artsdalen,E.R.;Yaffe,I.S.J.Phys.Chem.1955,59(2), 118.doi:10.1021/j150524a007

(26)Janz,G.J.;Allen,C.B.;Bansal,N.P.;Murphy,R.M.; Tomkins,R.P.T.Physical Properties Data Compilations Relevant to Energy Storage.II.Molten Salts:Data on Single And Multi-ComponentSaltSystems.1979.p.Medium:X; Size:Page:442.

(27)Jiang,T.;Wang,N.;Peng,S.;Yan,L.Chem.Res.Chin.Univ. 2015,31(2),281.doi:10.1007/s40242-015-4331-z

(28)Matsuura,H.;Watanabe,S.;Sakamoto,T.;Naoi,K.;Kitamura, N.;Akatsuka,H.;Adya,A.K.;Honma,T.J.Alloy.Compd. 2006,408－412,80.doi:10.1016/j.jallcom.2005.04.157

(29)Mariani,R.D.;Vaden,D.J.Nucl.Mater.2010,404(1),25. doi:10.1016/j.jnucmat.2010.06.022

(30)Janz,G.J.Molten SaltsHandbook;Academic Press:New York,San Francisco,London,1967.

(31)Scridharan,K.;Allen,T.;Anderson,M.;Simpson,M.Thermal Propertities ofLiCl-KClMolten Saltfor NuclearWaste Separtion,in NEUPFinalReport;University ofWisconsin-Madison:New York,San Francisco,London,2012.

Molecular Dynamics Simulation on the Structure and Thermodynamics of Molten LiCl-KCl-CeCl3

JIANG Tao1WANG Ning1CHENG Chang-Ming1PENG Shu-Ming1,*YAN Liu-Ming2
(1Institute ofNuclear Physicsand Chemistry,China Academy ofEngineering Physics,Mianyang 621999,Sichuan Province, P.R.China;2DepartmentofChem istry,College ofSciences,ShanghaiUniversity,Shanghai200444,P.R.China)

The struc ture and the rm odynam ics o f CeC l3inm olten LiC l-KC l-CeCl3m ixtu res w ere studied by molecu lar dynam ics simu lation.The re lationship formulas o f temperature and density,and composition and densitywere obtained.The firstpeak for the gCe-Cl(r)radialdistribution function was located at0.259 nm and the corresponding firstcoordination numberofCe3+was~6.9.This inconsistency betweenmolecu lar dynam ics and experimental data could be attributed to the fact that our values were obtained formolten LiCl-KCl-CeCl3m ixtures,in w hich the inte rac tion between Ce3+and C lwas m ore pow erful than that in pure m olten CeC l3. Regarding self-diffusion coe fficients,the activation energy ofCe3+was 22.5kJ∙mol－1,which is smaller than that ofU3+(25.8 kJ∙mo l－1).Furthermore,the p re-exponential factors for Ce3+decreased from 31.9×10－5to 21.8× 10－5cm2∙s－1as the mo lar fraction of Ce3+increased from 0.005to 0.05.This m eans tha t in the unit vo lum e (ignoring the change o f totalvolume),the diffusion resistance o fCe3+increased,and the self-diffusion ability decreased,which resu lted in a decrease of p re-exponential facto rs.

LiCl-KCl-CeCl3;Structure;Thermodynam ics;Mo leculardynam ics;Diffusion coefficient

October 28,2015;Revised:December 31,2015;Published onWeb:January 4,2016.

O641；O643

10.3866/PKU.WHXB201601042

*Corresponding author.Email:pengshuming@caep.cn.

Theprojectwas supported by theMajor Research Plan of theNationalNatural Science Foundation of China(91426302)and NationalNatural Science Foundation of China(21301163).