抑制斜拉桥施工阶段风致振动的水阻尼器可行性研究

李　宇， 潘　彪， 李　琛， 汪　洁， 高　亮

(1.长安大学 公路学院 旧桥检测与加固技术交通行业重点试验室, 西安　710064；2. 长安大学 建筑学院，西安　710064；3. 西安建筑科技大学 土木工程学院，西安　710055；4. 西安理工大学 土木建筑工程学院，西安　710048)



抑制斜拉桥施工阶段风致振动的水阻尼器可行性研究

李宇1， 潘彪1， 李琛2， 汪洁3， 高亮4

(1.长安大学 公路学院 旧桥检测与加固技术交通行业重点试验室, 西安710064；2. 长安大学 建筑学院，西安710064；3. 西安建筑科技大学 土木工程学院，西安710055；4. 西安理工大学 土木建筑工程学院，西安710048)

相对于成桥状态，斜拉桥最大双悬臂施工阶段的刚度低、阻尼小，更容易产生风致振动。建议了一种安装拆卸方便、成本较低的水阻尼器，并进行了CFD仿真分析和减振试验，以验证其抑制斜拉桥施工期风致振动的有效性。结果表明：① 水阻尼器能显著增大阻尼系数，减轻结构振动；② 过小的开孔率不能有效利用水阻尼器内部流体的黏滞作用来耗能，而过大的开孔率则使得水阻尼器上下游两个表面压力差减小严重；③ 在靠近水阻尼器两侧位置开孔，会使得外部绕流的旋涡在其两侧脱落；而靠近中心位置的开孔则可以使大漩涡在其下游面上脱落，有利于增大阻力系数；④ 侧孔对系统阻尼的影响将会随水阻尼器上下游两面开孔的不同而改变，过大或过小的侧面开孔都会显著降低阻尼系数；⑤ 水阻尼器体积的增大会降低减振效果，同时还应合理设计水阻尼器的最优的孔隙率，以达到最佳减振效果。综上所述，水阻尼器能有效抑制结构振动，且成本低廉、施工方便，特别适用于某些只需在施工期进行短期风振控制的桥梁。

斜拉桥；最大双悬臂施工；水阻尼器；风致振动；减振耗能

大跨斜拉桥在风力作用下易发生变形和振动，特别是它的施工阶段(最大单双悬臂状态)所受约束少，结构更轻柔，其抗风性能较成桥状态有很大降低。因此，有必要对斜拉桥施工阶段采取临时性的抗风措施。李永乐等[1]对大跨斜拉桥的施工阶段增设抗风临时拉索和利用塔旁托架，结果表明可以有效控制大桥抖振响应；康小英[2]对施工阶段的斜拉桥的桥塔进行了TMD制振措施的研究。唐启等[3]提出了将分幅式斜拉桥施工期主梁与墩旁的托架临时连接的经济有效的制振措施； 瞿伟廉等[4]提出了利用U型水箱对世纪桥施工双悬臂结构抖振控制的设计方法；宫成等[5]采取“下拉索+TMD”施工抗风措施有效地降低了桥梁结构风致振动响应；Dung等[6]研究了主动质量阻尼器(AMD)来提高桥梁节段模型的颤振稳定性；Xu等[7-8]提出采用多个TMD使其频率分布在一定范围内，则能提高控制系统的鲁棒性，以达到较好的减振效果；Kareem等[9-12]研究对比了单个调质阻尼器以及多重调质阻尼器的减振效果；袁小钦等[13]结合了磁流变阻尼器和调谐质量阻尼器，对MR-TMD减振装置进行了研究。虽然上述抗风减振措施都能取得一定的减振效果，但它们的造价较为昂贵且安装比较复杂[14-15]。因此，本文建议了一种成本较低、安装拆卸方便且不影响成桥后景观的水阻尼器，以保障大跨斜拉桥施工及人员的安全。

1　水阻尼器的设计思路

依据斜拉桥最大双悬臂施工阶段的结构特点，本文设计并布置了水阻尼器，具体步骤如下：

1) 制作蜂窝煤状的空心钢沉箱(图1)，除顶面外的其它各面都打孔，且各孔洞都是沿着水平向布置并贯穿钢沉箱；

2) 将水阻尼器沉没入水中，并用钢索将水阻尼器与加劲梁最大双悬臂的端部相连；

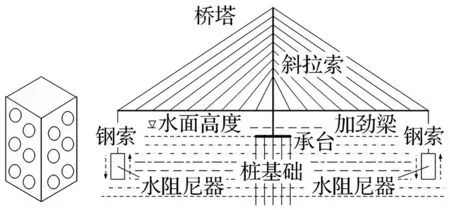
图1　水阻尼器及其布置Fig.1 Arrangement of water-damper

3) 当梁体发生风致振动时，会带动水阻尼器在水中上下运动，进而使水流不断进出水阻尼器；

4) 水阻尼器在水中运动受到的阻力分为压力与黏滞力两部分：

Fd=Fp+ Fv

(1)

式中：Fd为阻力；Fp为表面压力差；Fv为表面黏滞力。可以看出，大尺寸的水阻尼器表面压力和黏滞力大，从而能更有效地提供阻尼。另外，水流流经水阻尼器表面的小孔后，由于截面突然发生变化，水流将产生局部水头损失。局部水头损失与水流在孔洞处速度的平方成正比：

(2)

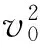
(3)

式中：Q为非保守力做的功，表示为水头损失的函数；T为水流运动的能量；U为水流运动的势能；η为水流距平衡位置的距离。

6) 根据式(1)～(3)可知，水阻尼器在水中的运动受到水流阻力的作用，这样即可不断消耗由加劲梁传递来的风致振动的能量，进而达到抑制加劲梁风致振动的目的。

7) 水阻尼器的适用条件：要求有较深的水位以满足水阻尼器在水流中的上下运动；若水流流速太大，可能会对水阻尼器产生影响，此时应在水阻尼器运动位置处设置注满水的钢管桩，使水阻尼器能在管内进行工作。

2　水阻尼器的CFD仿真分析

为验证水阻尼器减振效果的有效性，本文采用计算流体力学软件Fluent对其阻尼系数进行数值模拟分析。为减少计算量，将水阻尼器的三维模型简化为二维平面模型，这同样可以反映开孔直径、开孔间距、开孔率等因素对水阻尼器阻尼系数的影响。计算参数如下：① 水阻尼器模型尺寸20 cm×20 cm；② 水流密度ρ=1 000 kg/m3，黏度μ=1×10-3Pa·s；③ 水阻尼器上游为速度入口，两侧为对称边界，出口边界为充分发展流，模型表面为光滑壁面；④ 如图2所示，计算域大小的确定以边界条件不影响水阻尼器周围压力分布为准，入口与两侧与水阻尼器的距离均为100 cm，出口与水阻尼器的距离为200 cm；⑤ 采用二维5方程的雷诺应力模型来计算湍流，使用非定常流计算，在初始步骤迭代至阻尼系数稳定，以0.001 s的时间步长计算至5 s，最终的阻尼系数为5 s内的阻尼系数的平均值。

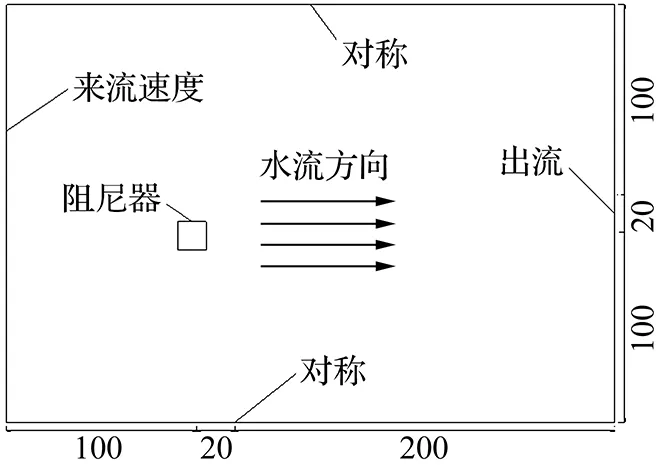
图2　计算域及边界设置Fig.2 Computational domain and boundary Settings

2.1无开孔的影响

首先计算了两个无开孔模型(20 cm×20 cm)的阻尼系数，并检验模型计算域网格的独立性。

模型1：在无开孔模型表面等分网格，间距2 mm，向计算域四个边界方向以1.06的渐变率增大间距，模型周围4 mm内设置4排边界层网格。网格划分形式如图3所示。

模型2：在无开孔模型表面等分网格，间距4 mm，向计算域边界方向以1.06的渐变率增大间距，模型周围4 mm内设置4排边界层网格。

计算结果显示：无开孔模型2与模型1的阻尼系数比为1.01，且其网格密度满足独立性要求。

图4为模型1第5秒时的压力云图与流迹线，可知：水流遇到模型后，流迹线发生卷曲，并在其两侧及后方产生旋涡，流迹线曲率大的位置旋涡强度大，旋涡产生的负压更强。在模型上下游两面的压力差值越大，模型产生的阻力越大。

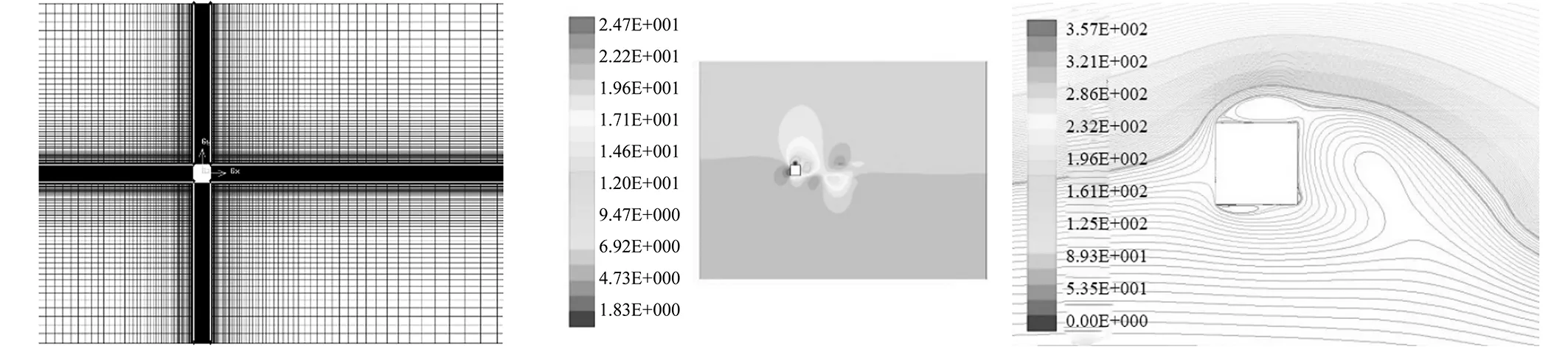
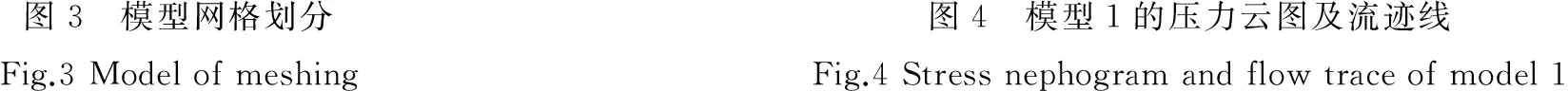
图3 模型网格划分Fig.3Modelofmeshing图4 模型1的压力云图及流迹线Fig.4Stressnephogramandflowtraceofmodel1

2.2顶底面开孔直径的影响

在模型1表面开孔，水流过小孔在内部形成紊流，动能耗散更快，增大模型阻尼系数。为确定单个开孔直径对模型阻尼系数的影响，设计在上下游两个表面中心位置开孔为1 cm、2 cm、3 cm和4 cm(图5)的四种模型(20 cm×20 cm)。

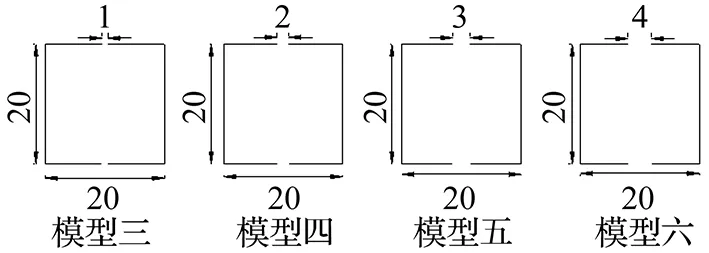
图5　模型3～6Fig.5 No.5～No.8 modals

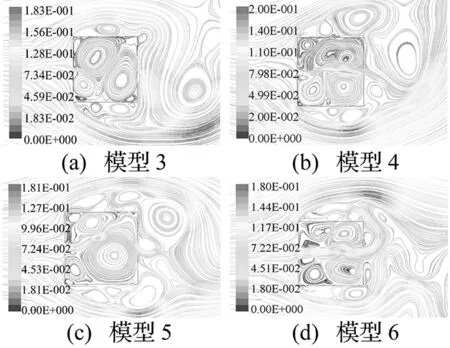
图6　模型3～6的流迹线Fig.6 Flow trace of No.3～6 modals

图6为模型3～6的流迹线，从中可以看出：

1) 模型开孔后，水流由孔口进入内部，带动内部流体运动，使内部产生了不同大小的旋涡，且这些旋涡的运动受到流体黏滞力的影响。旋涡运动越强烈，流体受黏滞力越大，从而耗散更多能量，就增大了模型的阻尼系数。但开孔也会减少表面压力，进而减少阻力系数。另外，开孔还会影响模型的外部绕流形式，从而影响阻力大小。

2) 模型3内部涡旋相对平缓，而模型4～6的内部涡旋相对复杂。随着开孔增大，模型下游孔口的流出速度增大。从图6(d)可以看出：水流几乎是从上游孔口径直流出下游孔口，而且模型6流入与流出水阻尼器的水流速度几乎相等，这必然减小水阻尼器的表面压力。

表1为模型3～6阻尼系数的计算结果，可知：与模型1的阻尼系数相比，模型3～4的阻尼系数较大，而模型5～6的阻尼系数较小。这是因为模型5～6表面压力损失较大。

表1　模型3～6的阻尼系数

2.3开孔间距的影响

为研究两孔间距对阻尼系数的影响，结合模型3～6的计算结果，本文设计了两组开孔直径分别为1 cm和2 cm的模型。

1) 第一组模型(图7)：开孔直径为1 cm，两孔净距为1～9 cm不等。

图7　模型7～11Fig.7 No.7～11 modals

图8和表2分别为模型7～11的流迹线和阻尼系数的计算结果，从中可以看出：

(1) 双孔的模型内部流迹线图较单孔的复杂，而且随着孔距增大，内部的旋涡转体积变小、数量增多，水流速率也增大。可见，随着孔距的增大，模型内部水流的黏滞力对能量的消耗增大。

(2) 开孔位置的不同也影响外部绕流的形式，如图8(b)所示，模型下游表面上附着两个旋涡，形成低压区，这显著增大了水流在流向对模型的作用力，从而增大了阻尼系数。

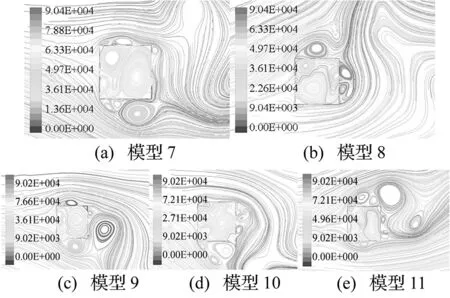
图8　模型7～11的流迹线Fig.8 Flow trace of No.7～11 modals

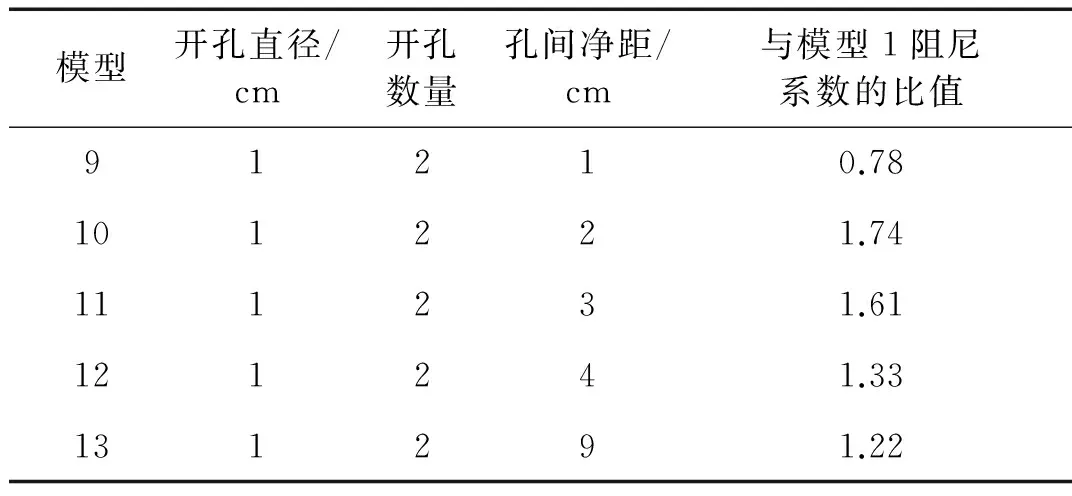
模型开孔直径/cm开孔数量孔间净距/cm与模型1阻尼系数的比值91210.78101221.74111231.61121241.33131291.22

2) 第二组模型(图9)：开孔直径为2 cm，两孔净距为1～9 cm不等。

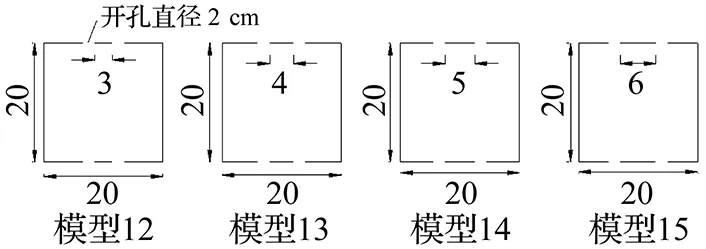
图9　模型12～15Fig.9 No.12～15 modals

图10　模型12～15的流迹线Fig.10 Flow trace of No.12～15 modals

图9和表3分别为模型12～15的流迹线和阻尼系数的计算结果，从中可知：直径2 cm的双孔模型内部的流迹线较孔径为1 cm的更加扭曲，流动形式更加复杂，耗能更多。但开孔间距对模型内部流动和外部绕流形式的影响并不明显。

表3　模型12～15的阻尼系数

综合表3～4可知：开孔直径1 cm的模型的阻尼系数比开孔直径2 cm的模型阻力系数大。可见，虽然后者内部的流动更为复杂，耗能更大，但不足以弥补开孔过大所损失的表面压力。

2.4开孔率的影响

由上可知：开孔1 cm、净距2～4 cm的模型阻尼系数较大。因此，按此标准，将开孔均布在模型上下游的两个表面，设计了模型16～18(图11)。

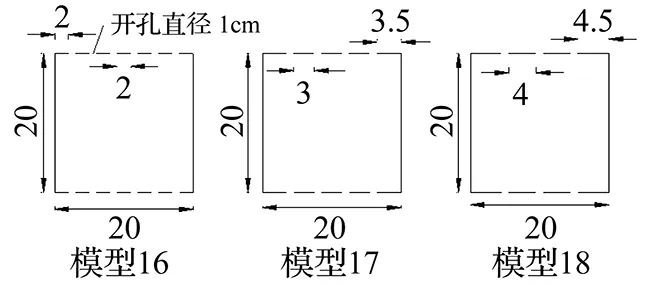
图11　模型16～18Fig.11 No.16～18 modals

图12为模型16～18的流迹线，从中可以看出：① 在模型16～18的孔间距下游处，流迹线曲折成圈，说明有旋涡形成。旋涡产生的低压会提高水流对模型的作用力，进而增大阻力系数。② 旋涡的脱落点也随开孔的增多而变化：大的旋涡从减振器两侧脱落，而在模型的下游面上有小旋涡脱落。③ 模型16～18的内部流迹线也没有显著有规律性的区别。表4为模型16～18的阻尼系数，可知：过多的开孔会使模型阻尼系数下降。

图12　模型16～18的流迹线Fig.12 Flow trace of No.16～18 modals

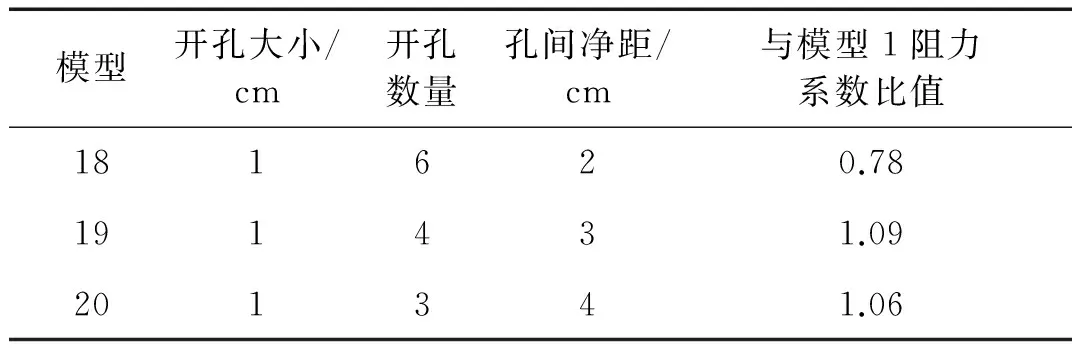
模型开孔大小/cm开孔数量孔间净距/cm与模型1阻力系数比值181620.78191431.09201341.06

2.5侧面开孔的影响

为了研究模型侧面开孔对阻尼系数的影响，将模型16～18的侧面中部开了1 cm的小孔(图13)，进行模拟计算。

图13　模型19～21示意图Fig.13 No.19～21 modals

图14为模型19～21的流迹线，从中可以看出：模型侧面开孔将会使得内部的流动变得非常紊乱，由不开侧孔时的大旋涡转变为数量众多的小旋涡。另外，在两孔间隔区域下游的旋涡依然存在，而且外部绕流从两侧脱落的旋涡也稍微变小。

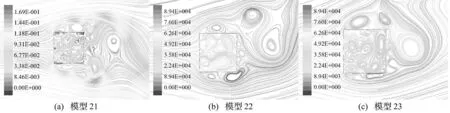
图14　模型19～21的流迹线Fig.14 Flow trace of No.19～21 modals

表5为模型21～23阻尼系数的计算结果，可知：模型侧面开1 cm的小孔能稍微增大阻尼系数。

2.6开孔分布形式的影响

由开孔率对阻尼系数的影响可知：模型开孔率在5%～10%的时候，其阻尼系数大部分都较高。因此，为研究开孔分布形式对阻尼系数的影响，本文设计了开孔分布形式不同但却具有相同开孔率的模型22～23(图15)。

表5　模型21～23的阻尼系数

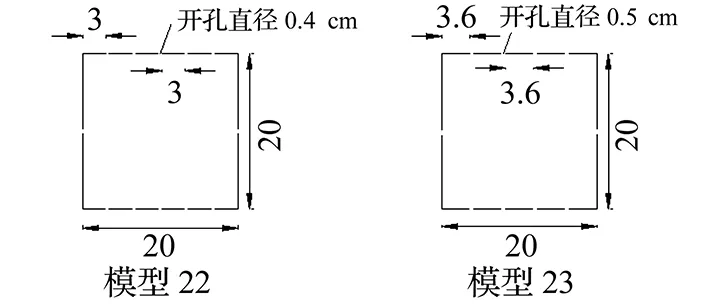
图15　模型22～23示意图Fig.15 No.22～23 modals

图16为模型22～23的流迹线，从中可以看出：开孔分布形式对模型22与23内部的旋涡尺寸的影响并不大，模型22与1的阻尼系数比为1.53，模型23与1的阻尼系数比值为1.31。

图16　模型22～23的流迹线Fig.16 Flow trace of No.22～23 modals

2.7侧面开孔直径的影响

为研究侧面开孔大小对模型阻尼系数的影响，在模型22两侧开不同直径的孔(图17)。

图17　模型24～26示意图Fig.17 No.24～26 modals

图18为模型24～26的流迹线，可知：侧孔会增加模型内部小规模旋涡的数量，对比三个模型，侧孔尺寸为2 cm的模型25内部流动最为紊乱。

图18　模型26～28的流迹线Fig.18 Flow trace of No.26～28 modals

表6为模型26～28的阻尼系数计算结果，可知：对模型23的侧面开孔会减小阻尼系数，但与开孔的大小并不线性相关；过大或过小的模型侧面开孔将会急剧减小阻尼系数；当孔径在2 cm时阻力系数则减少较小。

表6　模型26～28的阻尼系数

2.8CFD计算结果小结

1) 开孔式水阻尼器能显著增大系统阻尼。

2) 影响阻尼系数的首要因素是开孔率：过小的开孔率不能有效利用水阻尼器内部流体的黏滞作用耗能；而过大的开孔率则使得水阻尼器上下游两个表面压力差减小严重。

3) 相同开孔率时，开孔的分布形式对阻尼系数影响显著：即在靠近水阻尼器两侧位置开孔，会使得外部绕流的旋涡在水阻尼器两侧脱落；而靠近中心位置的开孔则可以使大漩涡在水阻尼器下游面上脱落，有利于增大阻力系数。然而，当单个开孔过大或孔间距过小时，水流将会通过水阻尼器径直从下游开孔流出，这就降低了水流阻力的作用，因此，开孔应靠近中部且有一定间距。

4) 侧孔对阻尼系数的影响将会随水阻尼器上下游两面开孔的不同而改变，过大或过小的侧面开孔都会显著降低阻尼系数。

3　水阻尼器的减振试验

基于上述CFD分析，选取了合适的开孔率、开孔直径、开孔间距和布孔方式，制备相应的试验模型，进行水阻尼器减振效果的试验研究。

3.1试验实施步骤

试验采用如下实验仪器：雕刻机、加速度计、激励装置、数据采集仪和自编软件等所组成的试验系统。具体步骤如下(图19)。

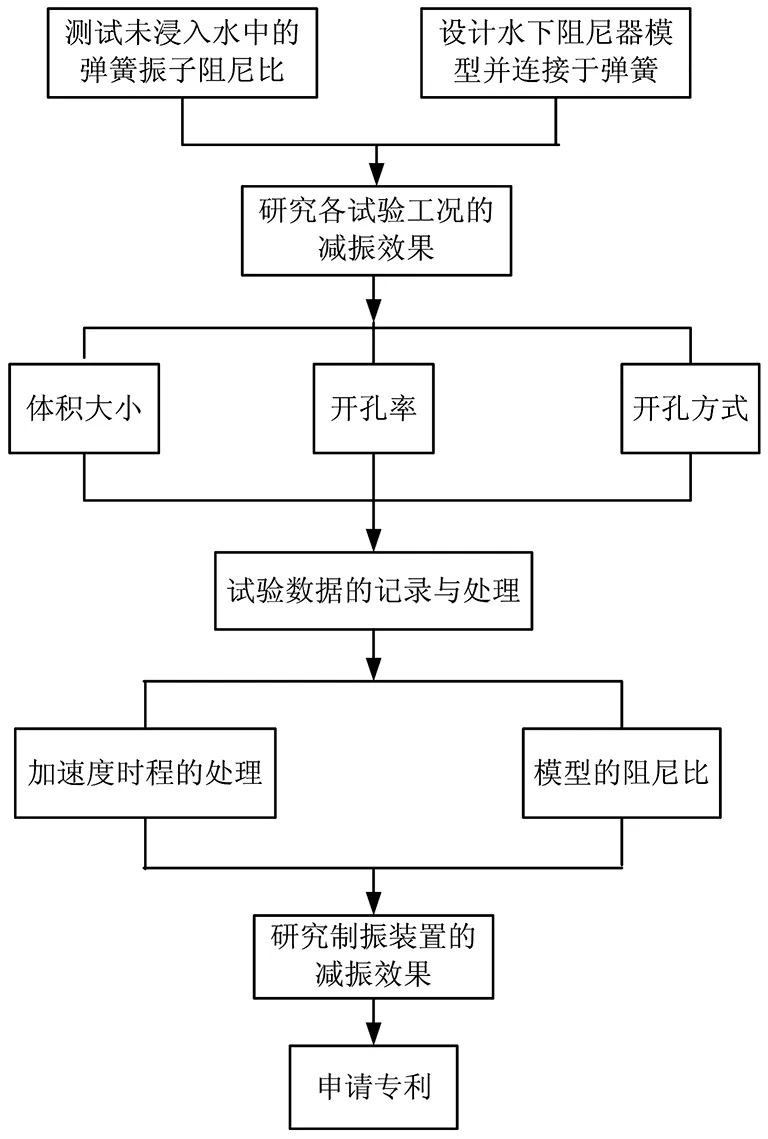
图19　试验的技术路线Fig.19 Technical route of test

1) 架设支架，并在其上吊挂弹簧；

2) 对弹簧施加初位移，再采用加速度计和数据采集仪测得弹簧的加速度时程曲线。弹簧的阻尼比用下式计算：

(4)

式中：ξ为阻尼比；n为计算阻尼比所选取的加速度时程的周期数；A2,A1分别为n个周期中的最大和最小加速度幅值。

3) 用雕刻机制作10 cm×10 cm×10 cm、15 cm×15 cm×15 cm、20 cm×20 cm×20 cm的空心立方体(图20)，每个立方体除顶面外的其它各面都打16个孔，三种立方体的孔洞直径分别为D=1.0 cm、1.5 cm、2.0 cm；

4) 在一大尺寸水桶中盛满水，以此来考虑水阻尼器所处的水体环境(此时的水桶即用来模拟空心钢管，而桶中的水则是静止的，进而达到避免外界水流流动对水阻尼器的影响)；

5) 如图21所示，将模型挂在弹簧上，并加上附加质量块令其沉入水中，同时，让弹簧倾斜一个微小的角度，进而采用激励装置对整个系统施加激励，使模型在水中上下振动，并附带左右晃动(以此来考虑施工桥梁的上下和水平振动)，此时再采用加速度计和数据采集仪测得弹簧加速度时程曲线，再用式4计算系统阻尼比；

6) 与初始弹簧的阻尼比进行对比，如果架设模型后的系统阻尼比有所增大，则说明所设计水阻尼器具有一定的减振效果，可以抑制斜拉桥施工阶段风致振动的效果。

图20　不同体积的水阻尼器模型Fig.20 Water-damper with different volumes

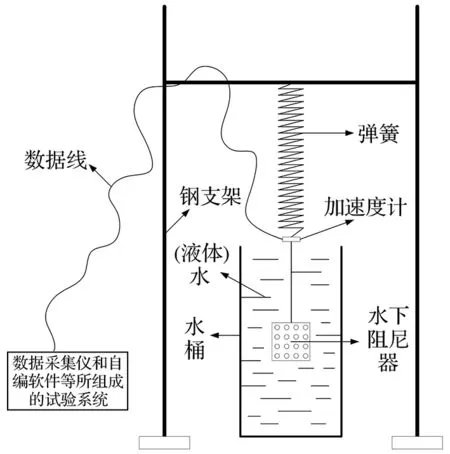
图21　水阻尼器的减振试验Fig.21 Vibration reduction test of water-damper

3.2试验结果分析

3.2.1水阻尼器的减振效果

图22给出了未架设水阻尼器的弹簧振子加速度衰减过程，图23则给出架设10 cm×10 cm×10 cm、15 cm×15 cm×15 cm、20 cm×20 cm×20 cm水阻尼器模型(孔隙率为3.14%、6.28%、9.42%、12.56%)的弹簧振子的加速度衰减过程。对比图22和图23可知：架设水阻尼器前的弹簧振子的系统阻尼比较小，其加速度衰减较为缓慢；而架设水阻尼器后的弹簧振子的系统加速度却衰减得十分迅速，这说明水阻尼器增大了系统阻尼，而且减振效果很显著。表7计算架设和未架设水阻尼器时的系统阻尼比，可知：架设水阻尼器后的系统阻尼比显著增大。

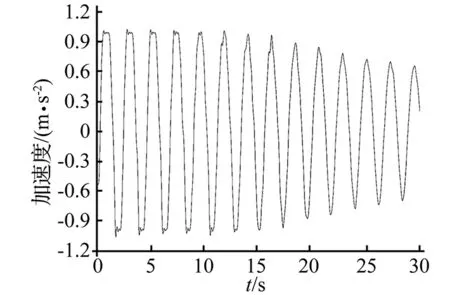
图22　未架设水阻尼器的系统加速度衰减过程Fig.22 System acceleration reduction without water-damper

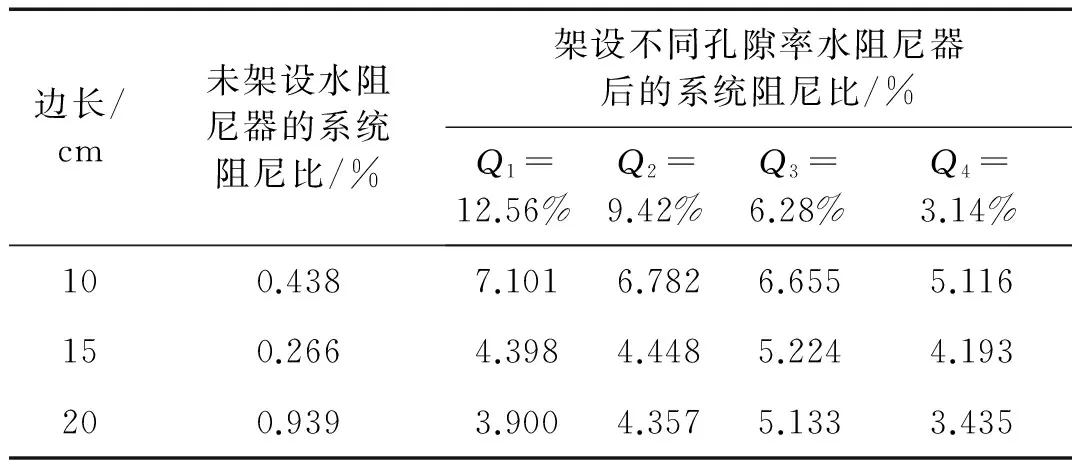
边长/cm未架设水阻尼器的系统阻尼比/%架设不同孔隙率水阻尼器后的系统阻尼比/%Q1=12.56%Q2=9.42%Q3=6.28%Q4=3.14%100.4387.1016.7826.6555.116150.2664.3984.4485.2244.193200.9393.9004.3575.1333.435

(a) 10cm×10cm×10cm(b) 15cm×15cm×15cm(c) 20cm×20cm×20cm图23 架设水阻尼器后的系统加速度衰减过程Fig.23Systemaccelerationreductionwithwater-damper

3.2.2不同体积大小的影响

本研究考虑三种不同的体积：10 cm×10 cm×10 cm、15 cm×15 cm×15 cm、20 cm×20 cm×20 cm，以探讨体积大小对水阻尼器减振性能的影响。从图24中可知：随着水阻尼器体积的增大，系统阻尼比呈递减趋势，这主要是因为水阻尼器的体积增大后，其浮力也随之增大，进而影响到系统阻尼比的增加，降低了水阻尼器的减振效果。可见，在实际工程中，应根据具体结构的规模来合理设计水阻尼器的大小，以达到最佳的减振效果。

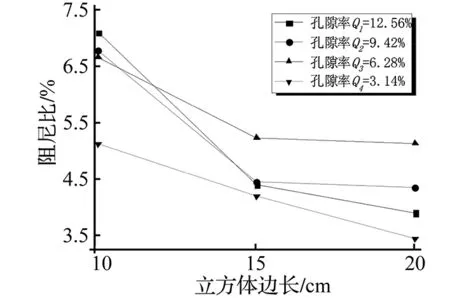
图24　体积大小对减振效果的影响Fig.24 Effect of volume on vibration reduction

3.2.3不同孔隙率的影响

开孔率的大小能影响通过水阻尼器的水流量，进而影响水流对水阻尼器所产生的阻力大小。因此，本文在保证同等过水面积的前提下，调整孔洞的个数和口径，进而研究了不同开孔率对水阻尼器减振效果的影响。从图25中可以看出：① 对于10 cm×10 cm×10 cm模型，随着孔隙率的增大，其系统阻尼比呈递增趋势，但当孔隙率超过6.28%，其系统阻尼比的增幅并不显著；② 对于15 cm×15 cm×15 cm和20 cm×20 cm×20 cm的模型，其系统阻尼比在孔隙率为6.28%时达到了峰值，之后则随着孔隙率的增大而减小。可见，水阻尼器的减振效果存在着一个最优的孔隙率。

图25　不同孔隙率对减振效果的影响Fig.25 Effect of porosity on vibration reduction

4　结　论

本文建议了一种安装拆卸方便、成本较低的抑制斜拉桥施工阶段风致振动的水阻尼器，并进行了CFD仿真分析和减振试验。

CFD仿真结果表明：① 水阻尼器能显著增大系统阻尼；② 过小的开孔率不能有效利用水阻尼器内部流体的黏滞作用耗能；而过大的开孔率则使得水阻尼器上下游两个表面压力差减小严重；③ 水阻尼器两侧位置开孔，会使得外部绕流的旋涡在水阻尼器两侧脱落；而靠近中心位置的开孔则可以使大漩涡在阻尼器下游面上脱落，有利于增大阻尼系数；④ 过大或过小的侧面开孔都会显著降低阻尼系数。

减振试验结果表明：① 水阻尼器增大系统阻尼，并能有效降低结构振动；② 水阻尼器体积的增大会降低减振效果；③ 水阻尼器的减振效果存在着一个最优的孔隙率。

综上所述，水阻尼器能有效抑制结构的振动，且成本低廉、施工方便，特别适用于某些只需在施工期进行短期风振控制的桥梁。

[1] 李永乐, 周述华, 张焕新. 某大跨度斜拉桥施工阶段的抖振控制措施研究[J]. 西南交通大学学报, 2001, 36(4): 374-377.

Ll Yong-le, ZHOU Shu-hua, ZHANG Huan-xin. Bueffting restraining measures for long span cbale-stayed bridges under construction [J]. Journal of Southwest Jiaotong University, 2001, 36(4): 374-377.

[2] 康小英. 桥塔独塔施工阶段抖振响应分析及制振措施的研究[D]. 成都:西南交通大学,2002.

[3] 唐启, 李鑫, 游新鹏,等. 基于抖振分析的分幅式斜拉桥施工期抗风措施研究[J]. 中国港湾建设, 2015, 35(6): 20-25.

TANG Qi, LI Xin, YOU Xin-peng, et al. Wind-resistance measures for separate during construction based on roadway cable-stayed bridge buffeting analysis[J]. China Harbour Engineering, 2015, 35(6): 20-25.

[4] 瞿伟廉, 秦顺全. 海口世纪大桥施工双悬臂阶段风致抖振反应的控制[J]. 土木工程学报, 1999, 32(3):41-47.

QU Wei-lian, QIN Shun-quan. Control of wind induced buffeting responses at twin-cantilever construction stage of the century bridge in haikou[J]. China Civil Engineering Journal, 1999, 32(3):41-47.

[5] 宫成, 刘志文, 谢钢,等. 高墩大跨斜拉桥悬臂施工期风致振动控制[J]. 工程力学, 2015, 32(增刊1): 122-128.

GONG Cheng, LIU Zhi-wen, XIE Gang, et al. Control of wind-induced vibraion in large span cable-stayed bridge with high piers during cantilever construction stages[J]. Engineering Mechanics,2015, 32(Sup1): 122-128.

[6] Dung N N, Miyata T, Yamada H. Application of robust control to the flutter in long-span bridges [J]. J. Struct. Engrg./Earthquake Engrg. JSCE, 1996, 42A: 847-853.

[7] Igusa T, Xu K. Wide band-response characteristics of multiple subsystems with high modal density [C]//Proceedings of the Second International Conference on Stochastic Structural Dynamics. USA, 1990.

[8] Igusa T, Xu K. Vibration reduction characteristics of distributed tuned mass dampers [C]//Proceedings of the Fourth International Conference on Recent Advances in Structural Dynamics. Southampton, UK, 1991.

[9] Kareem A, Kline S. Performance of multiple mass dampers under random loading[J]. Journal of Structural Engineering, 1995, 121(2): 348-361.

[10] Li Chun-xiang，Liu Yan-xia. Optimum multiple tuned mass dampers for structures under ground acceleration based on the uniform distribution of system parameters [J]. Earthquake Engineering and Structural Dynamics. ASCE1993.199(11)：2317-2320.

[11] Gu M, Xiang H F. Optimization of TMD for suppressing buffeting response of long-span bridges [J]. Journal of Wind Engineering & Ind. Aerodynamics,1992,42(44):1383-1392.

[12] Gu M，Chen S R，Chang C C. Parametric study on multiple tuned mass dampers for buffeting control of Yangpu Bridge[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89(11/12)：987-1000.

[13] 袁小钦, 刘习军, 张素侠. MR-TMD 减振系统对连续箱梁桥振动控制研究[J]. 振动与冲击, 2012,31(20):153-158.

YUAN Xiao-qin, LIU Xi-jun, ZHANG Su-xia. Continuous box girder bridge vibration control with MR TMD damper system [J].Journal of Vibration and Shock,2012, 31(20): 153-158.

[14] Scanlan R H, Jones N P. Aeroelastic analysis of cable-stayed bridge [J]. J. of Struct Energ. ASCE,1990,116(2):270-297.

[15] Ricciardelli F. Prediction of the response of suspension and cable-stayed bridge towers to wind loading[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 64: 145-159.

Water-damper for wind-induced vibration control of a cable-stayed bridge in its construction stage

LI Yu1, PAN Biao1, LI Chen2, WANG Jie3, GAO Liang4

(1. Key Laboratory of Ministry of Communications for Bridge Detection & Reinforcement Technology, School of Highway, Chang’an University, Xi’an 710064, China; 2. School of Architecture, Chang’an University, Xi’an 710064, China; 3. School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China; 4. School of Civil Engineering and Architecture, Xi’an University of Technology, Xi’an 710048, China)

As opposed to a finished cable-stayed bridge, wind-induced vibration can more easily be caused in max double-cantilever construction stage of a cable-stayed bridge because of its low stiffness and damping. Here, water-damper was suggested with its convenience and low cost. CFD Analysis and vibration reduction tests were carried on to study its effectiveness of vibration control. The results showed that ① the system damping increases significantly by applying water-damper with holes, the structural vibration can be reduced effectively; ② the effectiveness of water-damper drops with lower or higher opening hole rate; ③ if holes are opened at the edge of a water-damper, external flow vortices fall off; if holes are opened in the middle of a water-damper, the system damping increases; ④ the effects of holes in sides of a water-damper on the system damping vary with different positions of holes, the system damping decreases significantly with lower or higher opening hole rate of sides; ⑤ the effectiveness of water-damper drops with increase in its volume; the optimal opening hole rate should be designed to achieve the best effect of vibration reduction. It was shown that the wind-induced vibration can be controlled effectively by applying a water-damper with low cost and convenience, it is especially suitable for controlling wind-induced vibration of a cable-stayed bridge in its construction stage.

cable-stayed bridge; max double-cantilever construction; water-damper; wind-induced vibration; vibration reduction and energy dissipation

国家自然科学基金(51408042)；陕西省自然科学基础研究基金面上项目(2015JM5156)；陕西省教育厅专项科研项目(15JK1422)；西安市建设科技项目(SJW2014012)；中央高校基本科研业务费专项资金项目(0009-2014G1211006)

2015-03-19修改稿收到日期：2015-07-30

李宇 男，副教授，硕士生导师，博士后，1982年生

U448.27

A

10.13465/j.cnki.jvs.2016.15.002