切向加载、卸载和振荡强耦合下机床螺栓结合部之摩擦能量耗散机制
2016-09-13田红亮陈甜敏郑金华
田红亮, 余 媛, 张 屹, 陈甜敏, 郑金华
(三峡大学 机械与动力学院,湖北 宜昌 443002)
切向加载、卸载和振荡强耦合下机床螺栓结合部之摩擦能量耗散机制
田红亮, 余媛, 张屹, 陈甜敏, 郑金华
(三峡大学 机械与动力学院,湖北宜昌443002)
在保持微凸体受法向力恒定的状态下,侧重导出切向力和变形量的切向加载、切向卸载和切向振荡接触方程。当2个球形微凸体接触时,构建每循环中切向接触摩擦能量耗散力学模型。按照赫兹静力弹性法向接触理论,得到微凸体顶端曲率半径。根据微凸体分担法向力的光滑性与连续性法则,校正临界弹性变形微接触面积与临界变形量的数学表达式。面向有条件等式,在弹性和纯塑性变形基础上,建立整个结合部法向力与切向接触摩擦能量耗散的理论模型。以北京机电院高技术股份有限公司直线电机驱动Linear MC6000普莱诺五面体加工中心上的龙门横梁-导轨螺栓结合部为研究对象,分析法向预紧力、表面粗糙轮廓分形维数、切向力、分形粗糙度、相关因子、单轴向屈服应变及静摩擦因数等7个相对独立参数对切向接触摩擦能量耗散的影响规律。可视化的数值分析结果表明:切向接触摩擦能量耗散随着法向预紧力的增大先增大后减小;表面粗糙轮廓分形维数在较小范围内,切向接触摩擦能量耗散随着表面粗糙轮廓分形维数或分形粗糙度的增大而增大;表面粗糙轮廓分形维数在较大范围内,切向接触摩擦能量耗散随着表面粗糙轮廓分形维数或分形粗糙度的增加而减小;切向接触摩擦能量耗散随着切向力、相关因子、单轴向屈服应变的增加而加大;切向接触摩擦能量耗散随着静摩擦因数的增加而降低与经典结论完全相反,这是因为当静摩擦因数较大时,根据近代分形几何理论可知法向预紧力越大,微滑趋势将更小,导致较小切向接触摩擦能量耗散。
切向加载;切向卸载;切向振荡;机床;螺栓结合部;法向预紧力;切向交变力;摩擦能量
机床量大面广,能量耗散多,能量利用率低,节能降耗潜力大。机床能量耗散是一个多部件多层次的系统问题,在未来能量耗散指标将成为评价机床产品的一个新指标。针对揭示机床的能量特性、构建机床能量耗散模型,国内外学者开展了大量的研究工作,以探寻节能降耗途径、减少环境污染、推动绿色与可持续制造的发展。
一般普通机床中,总刚度的60%~80%来自结合部的接触刚度,总阻尼的90%以上源自结合部接触阻尼。结合部接触阻尼与能量耗散直接相关,如在钢筋混凝土结构里,振动阻尼系数越大越好,消能越快,不致使结构引起谐振。螺栓联接结合部是机床中最为典型的一种结合部形式,其影响因素众多,作用机理极其复杂,具有强非线性特征。许多学者一直在其力学特性研究上进行不断的探索。2011~2016年本课题组所做的许多肤浅研究尽管从微宏观机理上尝试性地定性或定量解释一些因素对螺栓联接结合部静动态特性的影响规律[1-28],但是由于螺栓联接结合部试验模型的排它性,结合部的不相容性,非线性来源的不确定和不明确性,试验结果的不可测量性、无重复性以及时变特性等一系列复杂问题,使得结合部的能量耗散研究变得愈发艰辛。20世纪80年代末,日本著名学者伊东谊对机床结合部研究的历史进行了回顾与展望,他认为确定结合部阻尼及其衰减能的理论计算方法依然没有得以解决,从此以后,结合部的研究便进入了一个低潮期。所以综述能量耗散研究,理清研发思想,对于进一步把握其内在机制具有重大作用。引起螺栓联接结合部能量耗散产生的原因很多,如结合部间的微观滑移和局部撞击、外界复杂动载荷以及润滑油膜等复杂因素,使得螺栓联接结合部具有非线性特点、迟滞特征和复杂的动力特性。但现存研究对螺栓联接结合部能量耗散鲜见确切的公认研究定论,因此要分清螺栓联接结合部的能量耗散性质,探索其内在真正机理,是一个值得探索与颇有挑战性的课题。
姚运萍等[29]修正了螺栓联接结合部能量损失与载荷幅值间的数学关系。张学良等[30-31]建立了平面结合部切向接触阻尼的分形模型,平面结合部法向载荷增大时,平面结合部的切向接触阻尼耗能减小,平面结合部切向接触阻尼损耗因子随着结合部粗糙度的减小而减小。李小彭等[32]提出结合部的“固-隙-固”接触模型,建立考虑摩擦因素影响的结合部切向接触阻尼的分形预估模型,结合部的切向接触阻尼随结合部实际接触面积的增大而增大,随结合部法向载荷的增大而减小,随结合部间摩擦因数的增大而趋于恒定。然而,以上文献求解机床螺栓联接结合部能量耗散的办法存在1个同样弊端:已有多篇参考文献的交叉综合引用太多,完全基于作者专业知识的系统性推导太少,理论的全新原创性较少,没有从引起机床螺栓联接结合部能量耗散的核心机制和本质原因建立能量耗散方程,不同文献给出的理论结论相互矛盾或不一致,甚至某些文献的理论定性论断与试验结果恰好相反和冲突,现有文献中理论给人的信任感及可信度太差,更无法进一步谈论绝对误差和相对误差的定量验证。有关机床螺栓联接结合部能量耗散的研究,仅仅局限于理论。而如何将机床螺栓联接结合部能量耗散基础数据应用于工程实际中,通过试验评价和验证其正确性和适用性,最终预测出机床螺栓联接结合部能量耗散性能,是将基础科学问题的研究结果应用于工程实际中的又一难点,也是必须攻克的科研难题。通过机理研究建立机床螺栓联接结合部能量耗散本构模型,揭示其内在本质规律,使得所创模型符合生产实际,如同牛顿第二定律F=ma和1882年赫兹静力弹性法向接触理论一样,具有精准通用性,是科学技术工作人员、专家和学者所追求的梦想和奋斗目标。
在原子级平坦的晶体界面摩擦试验中,摩擦并未完全消失,有时还相当可观。这说明除了塑性变形、粗糙峰啮合和黏着等宏观的摩擦机理外,还存在着更为基本的能量耗散过程而导致摩擦的产生,因此,从微观上进行摩擦能量耗散过程的研究对探索摩擦起源和摩擦控制具有重要的意义。摩擦过程是非线性的且远离平衡态的热力学过程。从本质上看,摩擦是在外力的作用下,发生相对运动或具有相对运动趋势的物体,受到与其相接触的物质或介质的阻力作用,在其界面上产生的一种能量转换现象。当2个表面作相对运动时,引起运动改变的力就做功,因此在接触的表面上有能量损耗。
上述问题是如此的复杂,以至于还不能被很好地解决。在保持微凸体受法向力恒定的状态下,侧重建立了切向力和变形量的切向加载、切向卸载、切向振荡方程,导出了2个球形微凸体接触时,每循环中切向接触摩擦能量耗散力学模型。使用赫兹静力弹性法向接触理论获得微凸体顶端曲率半径,按照微凸体分担法向力的光滑性与连续性原则,修订临界弹性变形微接触面积与临界变形量,面向有条件等式,区分弹性变形及纯塑性变形,建立整个结合部法向力、切向接触摩擦能量耗散的理论模型。根据所创建的模型,以北京机电院高技术股份有限公司直线电机驱动Linear MC6000普莱诺五面体加工中心龙门横梁-导轨作研究对象,给出法向预紧力p、表面粗糙轮廓分形维数D、切向交变力Q、分形粗糙度G、相关因子K、单轴向屈服应变φ、静摩擦因数f(满足fp≫Q)等7个相对独立参数对切向接触摩擦能量耗散W的影响规律,解释了产生影响规律的原因。其中,静摩擦因数对切向接触摩擦能量耗散的影响规律与经典结论不同。
1 固定结合部摩擦能量耗散机制
试验表明,弹性材料特别是金属材料表现出一种结构阻尼的性质。这种阻尼是由于材料受力变形而产生的内摩擦,干摩擦会消耗能量,力和变形之间产生了相位滞后,这种曲线叫做迟滞曲线。两微凸体同时受法向力和切向力,在保持法向力恒定的状态下,再施加切向力。切向力按施加顺序可分为3类:切向加载力、切向卸载力、切向振荡力。
1.1微凸体受法向恒定力和切向加载力
切向力从0单调增加时,微滑接触圆环的内半径(或黏附接触圆的半径)[33]为
(1)
式中:r为微滑接触圆环的外半径;f为静摩擦因数;N为微凸体所受的法向力;T为微凸体所受的切向力。
可见,随着切向力的增大,黏着区域轴对称地缩减;当切向力达到fN时黏着区域缩小至一点,随即发生整体滑动。
切向牵引力在接触面上的分布[34]为
式中:正体脚标L代表Loading的首字母;ρ为极半径;π为圆周率。
切向加载应力随着极半径的变化如图1所示的曲线r-A-B。
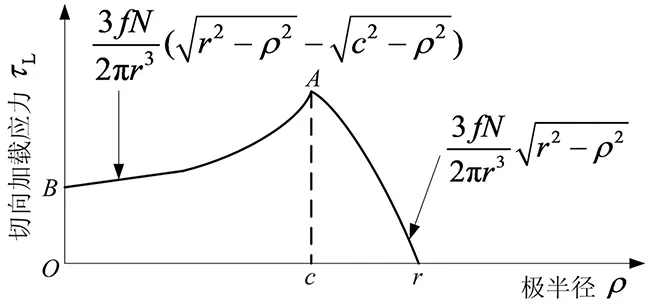
图1 切向加载应力与极半径的切向加载联系Fig.1 Tangential loading relation between tangential loading stress and polar radius
远方点相对于黏附部分的均匀变形量为
(3)
式中:μ为微凸体1或2的切变模量;v为微凸体1或2的泊松比。
由式(1)得
(4)
将式(4)代入式(3)得
(5)
切向力随着变形量的变化如图2所示。
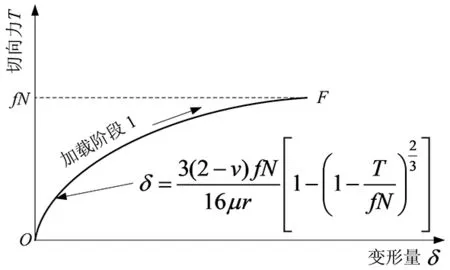
图2 切向力和变形量的切向加载迟滞曲线Fig.2 Tangential loading hysteresis curve between tangential force and deformation
切向加载柔度为
(6)
图2中,在点O处切向加载初始柔度为
(7)
图2中,在点F处切向加载终身柔度为
(8)
由式(8)知,当切向力T增加到一定值fN时,切向加载刚度接近于0,这正是意料之中的事情,这是因为此时接触界面将由微观滑移转化为宏观自由滑动,摩擦界面连接失效。
1.2微凸体受法向恒定力和切向卸载力
切向力从最大值T*缓慢减小时,根据图1,当极半径ρ=r时,微滑开始。与式(2)的第2个表达式类似,在c,r之间会产生一个临时穿透半径b。因为切向卸载与加载时,微凸体的变形方向相反,按照牛顿第三定律(每一个作用总是有一个相等的反作用和它相对抗;或者说,两物体彼此之间的相互作用永远相等,并且各自指向其对方),切向牵引力的变化是式(2)的-2倍。类比式(2)可得切向卸载时切向牵引力的改变量为
(9)
式中:正体脚标c表示change的首字母。
特别使人感到惊奇的是,用-2乘式(2),再以b代替c可得式(9),下文还将使用此结论。在式(9)与(2)之间存在一种反向放大2倍自然对称美。
切向卸载应力变化量随着极半径的变化如图3所示的曲线r-A′-B′。
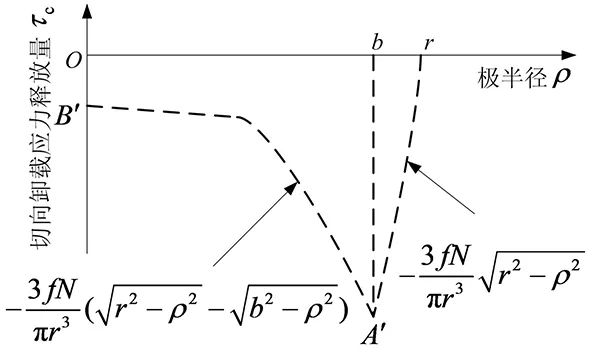
图3 切向卸载应力释放量与极半径的切向卸载联系Fig.3 Tangential unloading relation between tangential unloading release stress and polar radius
初始切向牵引力式(2)加切向应力变化量式(9)可得切向卸载时切向牵引力在接触面上的分布。为了直观地求得合成结果,现将图1与3画在同一幅图4中。

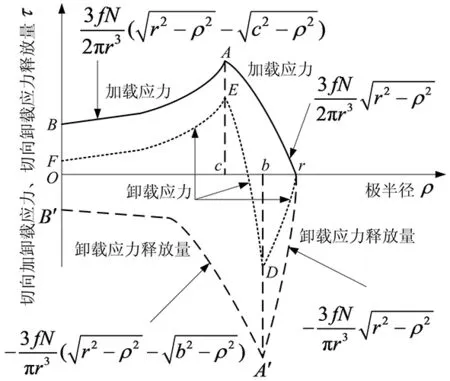
图4 切向加载应力、切向卸载应力释放量与极半径的关系Fig.4 Relation among tangential loading stress, tangential unloading release stress and polar radius
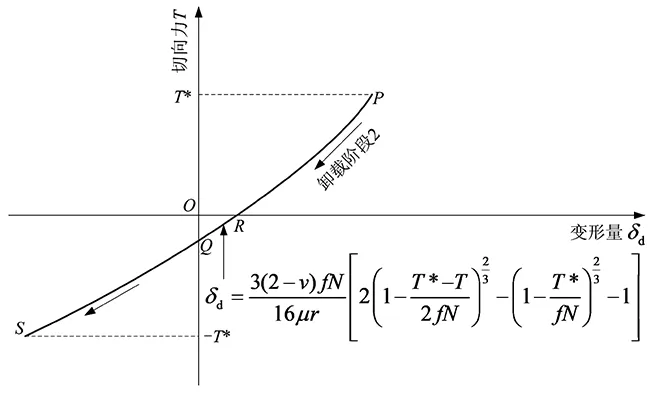
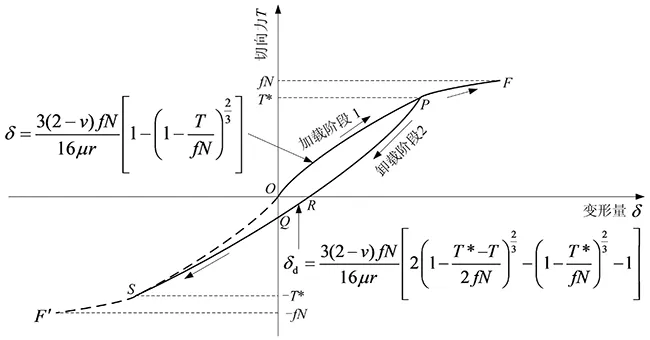
按照图4,当0≤ρ (10) 式中:正体脚标u表示unloading的首字母。 通过图4,当c≤ρ (11) 根据图4,当b≤ρ≤r时,切向卸载时切向牵引力在接触面上的分布为 (12) 将式(10) ~(12)合写成1个公式,可得切向卸载时切向牵引力在接触面上的分布为 (13) 切向卸载应力随着极半径的变化如图5所示的曲线r-D-E-F,其中曲线F-E对应式(10),曲线E-D对应式(11),曲线D-r对应式(12)。 图5 切向卸载应力与极半径的切向卸载关系Fig.5 Tangential unloading relation between tangential unloading stress and polar radius 将图4与5画在同一幅图6中,可分析3种切向应力之间的联系,其中曲线r-D-E-F是曲线r-A-B与r-A′-B′之和。 图6 切向加载应力、切向卸载应力释放量、切向卸载应力与极半径的关系Fig.6 Relation amongst tangential loading stress, tangential unloading release stress, tangential unloading stress and polar radius 根据图5,整个赫兹接触表面S={(ρ,θ)|0≤ρ≤r,0≤θ≤2π},切向卸载应力应满足赫兹平衡条件 (14) 注意到式(13)中的τu与θ无关,式(14)可简化为 (15) 把式(13)代入式(15)得 (16) 以下一元函数定积分为 (17) 将通解式(17)代入式(16)得 (18) 式(18)右边的第一项为初始切向力T*,就是 (19) 将式(19)代入式(18)得 (20) 由式(20)可得对应微滑的穿透深度为 (21) 切向卸载时,切向力T逐渐变小,其范围是-T*≤T≤T*。当T=-T*时,切向力完全反向,将T=-T*代入式(21)可得最小值 (22) 式(22)中的T*≥0与式(1)中的T≥0匹配(下文还将沿用此结论),再由式(22)与(1)得 bmin=c (23) 此时对应微滑穿透到初始微滑深度。将式(23)代入式(13)得 (24) 由式(24)与(2)可得τu=-τL,此亦是意料之中的结果,表明式(13)满足一个边界条件。 当T=T*时,切向力彻底正向,将T=T*代入式(21)可得最大值 bmax=r (25) 综合式(23)与(25)这两种极端情况,可得b的范围为 c=bmin≤b≤bmax=r (26) 将式(26)代入式(20)可知T≤T*,这还是意料之中的事情。式(26)与图6一致,将c≤b≤r代入式(9)可得τc≤0,这也是意料之中的事情。 将式(25)代入式(13)得 (27) 由式(27)与(2)可得τu=τL,这又是意料之中的成果,说明式(13)满足第二个边界条件。 前已述及,用-2乘式(2),再以b置换c可得式(9)。类似地,用-2乘式(3),再用b接替c可得切向卸载时远方点相对于黏附部分均匀变形量的改变量为 (28) 初始均匀变形量式(3)加均匀变形量的增量式(28)可得切向卸载时均匀变形量为 (29) 式中:正体脚标d表示decreasing的首字母。 由式(21)得 (30) 将式(30)代入式(29)得 (31) 前已提及,式(22)中的T*≥0与式(1)中的T≥0对应,用T*替换式(1)中的T可得 (32) (33) 将式(33)代入式(31)得 (34) 切向力随着变形量的变化如图7所示。 图7 切向力和变形量的切向卸载迟滞曲线Fig.7 Tangential unloading hysteresis curve between tangential force and deformation 切向力T从最大值T*缓慢减小到0时,即T=0在式(34)中对应的永久变形量为 (35) 式中:正体脚标p表示permanent的首字母。 幂函数f(x)=xμ(0<μ<1)在半开无限区间x∈[0,+∞)上连续,其图形是向上凸的曲线弧,那么对[0,+∞)上任意两点x1,x2恒有[35] (36) (37) 将f(x)=xμ代入式(37)得 (38) 因为0<μ<1,可令μ=2/3,将其代入式(38)得 (39) 将式(39)代入式(35)得 δdp>0 (40) 图7中,永久变形量δdp用线段OR表示。将T=0代入式(21)得 (41) 将式(41)代入式(13)可得当T=0时,τu≠0。将图2与7画在同一幅图8中,可分析2种变形量之间的联系,其中曲线OS与加载曲线OP关于原点中心对称。 图8 切向力和变形量的切向加卸载迟滞曲线Fig.8 Tangential loading and unloading hysteresis curve between tangential force and deformation 由式(5)得 (42) 由式(34)得 (43) (44) 图8中,加载曲线OP在T=T*时的变形量等于卸载曲线P-R-Q-S在T=T*时的变形量,即加载曲线与卸载曲线在切向力的最大值处相遇。切向卸载柔度为 (45) 图8中,在点P处切向卸载初始柔度为 (46) 由式(7)与(46)得 (47) 图8中,卸载曲线PR在点P处的斜率等于加载曲线OP在点O处的斜率。由式(34)得 (48) (49) 加载曲线OP的方程为式(5)。因为任何2个点(x,y)和(-x,-y)关于原点是对称的,故任何2个函数y=f(x)与y=-f(-x)的图像关于原点中心对称。因曲线OS与加载曲线OP关于原点中心对称,故曲线OS的方程为 (50) (51) 由式(48)、(49)和(51)得 (52) 图8中,T=-T*时的变形量等于T=T*时变形量的相反数,即点S的横坐标等于点P横坐标的相反数。由式(45)得 (53) 由式(6)得 (54) (55) 图8中,卸载曲线P-R-Q-S在点S处的柔度等于加载曲线OP在点P处的柔度。 1.3微凸体受法向恒定力和切向振荡力 δi=-δd(-T) (56) 将式(34)代入式(56)得 (57) 切向力随着变形量的变化如图9所示。 图9 切向力和变形量的切向振荡迟滞曲线Fig.9 Tangential oscillation hysteretic curve between tangential force and deformation 将图7与9画在同一幅图10中,可分析2种变形量之间的联系,卸载阶段P-R-Q-S与振荡阶段S-U-V-P横贯成一个封闭滞后回线P-R-Q-S-U-V-P。其中阶段3为振荡阶段,文献[29]称阶段3为“加载”,混淆了2个至关重要概念——振荡与加载,其计算原理是彻底错误的。 图10 切向力和变形量的切向卸载、振荡完整封闭环道Fig.10 Tangential unloading and oscillating whole closed circuit between tangential force and deformation 切向振荡柔度为 (58) 图9中,在点S处切向振荡初始柔度为 (59) 由式(59)和式(46)得 (60) (61) (62) 式中:TV为点V的纵坐标。 式(61)减式(62)可得回路P-R-O-V-P的面积为 (64) 式(63)加式(64)可得回路P-R-U-V-P的面积为 (65) (66) (67) 式中:TQ为点Q的纵坐标。 式(66)减(67)可得回路S-U-O-Q-S的面积为 SS-U-O-Q-S=SS(-T*)OU-SS(-T*)Q= (68) (69) 式(68)加(69)可得回路S-U-R-Q-S的面积为 (70) 试验表明,对材料反复加载、卸载和振荡,其力-变形曲线会成为一个滞后回线,此回线所围的面积表示一个循环中材料以热能形式耗散掉的能量。式(65)加(70)可得回路P-R-Q-S-U-V-P的面积为 F=SP-R-Q-S-U-V-P=SP-R-U-V-P+SS-U-R-Q-S= (71) 式(34)减式(57)得 (72) 将式(72)代入式(71)可得每循环中摩擦能量耗散为 (73) 下列2个一元函数定积分分别为 (74) (75) 将式(74) ~(75)代入式(73)得 (76) m为任意实数,将函数(1+x)m展开成x的幂级数[36] (-1 (77) (78) (79) 将式(78) ~(79)代入式(76)可得一个球形微凸体与刚性光滑平面接触时,每循环中摩擦能量耗散为 (80) 球形微凸体1和刚性光滑平面接触时,每循环中摩擦能量耗散为 (81) 式中:μ1为微凸体1的切变模量;v1为微凸体1的泊松比。 球形微凸体2与刚性光滑平面接触时,每循环中摩擦能量耗散为 (82) 式中:μ2为微凸体2的切变模量;v2为微凸体2的泊松比。 球形微凸体1与2接触时,每循环中摩擦能量耗散为 (83) 式中:G′为两接触材料的当量切变模量。式(83)不同于文献[30]中的式(1)。 将图2与10画在同一幅图11中,可获得3种变形量之间的联系。切向力T从0线性正向加载到额定力T*时,此为加载阶段OP;切向力T从最大值T*缓慢减小到-T*时,当T取负数时,表示作用力T的方向与加载阶段的作用力方向相反,即切向力T从额定力T*逐渐卸载至0,然后反向线性加载到额定力T*,此为卸载阶段P-R-Q-S;切向力T从最小值-T*增加到最大值T*时,即切向力T从额定力T*逐渐卸载至0,再继续正向加载至额定力T*,此为振荡阶段S-U-V-P。 图11 三个阶段的完整切向迟滞曲线Fig.11 Whole tangential hysteresis curves with three stages 2.1弹性变形时单个微凸体分担的法向力 处处连续、统计学自相似性、点点不可微的Weierstrass-Mandelbrot函数为 (84) 式中:n1为最低频率的初始项;γ为谱密度的尺度参数;x为表面的采样长度坐标。 式(84)的振幅即微凸体顶端的变形量 (85) 式中:a为单个微凸体的接触面积。 由赫兹点接触理论可得微凸体顶端曲率半径为 (86) 将式(85)代入式(86)得 (87) (88) 然后再由曲率半径的计算公式得到微凸体顶端的曲率半径为 (89) 将式(88)代入式(89)得 (90) 这就是文献[37]中式(7)的来龙去脉,用点点可微的1项余弦函数式(88)完全替代点点不可微的Weierstrass-Mandelbrot无穷项余弦级数式(84),依旧照搬2316年前希腊数学家欧几里得的几何学。1842年在数学上提出一致收敛概念的Weierstrass于1872年7月18日在柏林科学院的一次讲演中,构造了一个连续函数却处处不可微的例子,由此一举改变了当时一直存在的“连续函数必可导”的重大误解,震惊了整个数学界。数学家、分形几何之父、描述自然界粗糙度的Mandelbrot,生前试图寻找一种被称之为“数学怪物”的东西,人们无法用传统的Euclid几何语言去描述其局部和整体性质,可描述自然界的不规则现象,将工程表面形貌的轮廓线和岛屿的海洋线类比,提出表面的高度函数。文献[37]求解微凸体顶端曲率半径的方法不仅违背了赫兹点接触理论,而且不符合Weierstrass的不可微数学反例,更不符合Mandelbrot的分形本质要求。文献[37]虽然提出了类似式(86),却无勇气使用此公式,所以文献[37]是带有缺陷的分形理论,迫切需要纠正,本文的正解式(87)是文献[37]的有力补充。文献[37]提出的错误式(90)一直被全世界的广大科技工作者尤其是国内的高校人员原封不动地沿袭至今,一个主要原因是英文文献比中文文献受重视,中文学者无魄力挑战英文文献的错误和既定框架,文献[37]提出的错误式(90)成为分形理论飞速向前发展的绊脚石。 单个微凸体分担垂直于结合部的法向力为 (91) 由式(86)得 (92) 将式(92)代入式(91)得 (93) 将式(87)代入式(93)得 (94) 图1中,单个微凸体处于弹性变形时,其弹性接触面积为 ae=πr2=πRδ (95) 由式(86)得 πRδ=a (96) 将式(96)代入式(95)得 ae=a (97) 2.2纯塑性变形时单个微凸体担负的法向力 单个微凸体处于弹塑性变形时,单个微凸体的弹塑性接触面积(单个微凸体的弹性接触面积、纯塑性接触面积均为下面公式的特例)[20]为 aep=πR(2δ-δc) (98) 式中:δc为单个微凸体的临界变形量。 当2δ≫δc时,单个微凸体处于纯塑性变形时,其纯塑性接触面积为 (99) 将式(96)代入式(99)得 app=2a (100) 单个微凸体处于纯塑性变形时,其负担的法向力为 pp=Kσyapp (101) 式中:K为硬度与最初屈服强度之比而成的相关因子;σy为较软材料的最初屈服强度。 将式(100)代入式(101)得 pp(a)=2Kσya (102) 式(102)不同于文献[37]中的式(15)Pp(a)=Kσya,不符合机械工程的由来是,当单个微凸体处于纯塑性变形状态时,依旧选定弹性变形计算式(97),即Pp(a)=Kσyae=Kσya。 2.3整体结合部担当的总法向力 从弹性接触连续迁移到纯塑性接触时,单个微凸体发生的临界变形量为 (103) 式中:d为待定量纲一正系数。 将式(87)代入式(103)得 (104) 式(85)除以式(104)得 (105) 若δ=δc,此时由式(105)可得特解a,即为从弹性接触连续转化到纯塑性接触时相应的临界弹性变形微接触面积 (106) 将式(106)代入式(105)得 (107) ac在式(94)中对应的单个微凸体法向弹性力为 (108) ac在式(102)中相应的单个微凸体法向塑性力为 pp(ac)=2Kσyac (109) 两接触粗糙表面在缓慢加大的整体结合部总法向力作用下,单个微凸体会承担一部分法向弹性力或塑性力。如果作用在单个微凸体上的法向弹性力函数(见式(94))或塑性力函数(见式(102))在元素ac处汇交,可令式(108)与(109)相等 (110) 将式(104)中φ的定义式代入式(110)得 (111) 将式(106)代入式(111)得 (112) 将式(112)代入式(103)得 (113) 将式(112)代入式(106)得 (114) 微接触点的面积概率密度为 (0 (115) 式中:aL为最大接触点的接触面积。 整体结合部上的真实接触面积为 (116) 将式(115)代入式(116)得 (117) 作用于整个结合部上的法向预紧力为 (118) 将式(94)和(102)代入式(118)得 (119) 将式(115)代入式(119)得 p(aL>ac)= (120) 式(120)不同于文献[30]中的式(9) ~(10)。 将式(95)代入式(97)得 a=πr2 (121) (122) 将式(122)代入式(83)得 (0 (123) 各微凸体所受的力与其接触面积的大小成正比,作用于a上的切向力可以表示为 (124) 式中:Q为作用于整个结合部上的切向力。 将式(124)代入式(123)得 (0 (125) 作用于a上的法向力为 (126) 将式(126)代入式(125)得 (0 (127) 式(127)不同于文献[30]中的式(4)。 整个结合部的摩擦能量耗散为 (128) 将式(127)代入式(128)得 (129) 将式(115)代入式(129)得 (0 (130) 将式(117)代入式(130)得 (131) 式(131)不同于文献[30]中的式(8)。 可通过研究法向预紧力p与摩擦能量耗散W的关系来分析一个简谐振动周期内的接触阻尼耗能。根据式(120)及(131),p与W皆为aL的单值显函数。所以通过中间自变量aL,已知工程数据p和待求未知数W形成了一个隐函数。但困难的是,不能将p和W之间的隐函数化成显函数,最后式(120)及(131)组成了固定结合部摩擦能量耗散的完整预判模型。 以北京机电院高技术股份有限公司直线电机驱动Linear MC6000普莱诺五面体加工中心作研究对象,设计与制造了如图12所示的龙门横梁-导轨,该龙门横梁-导轨由尺寸都是1505 mm×63 mm×58 mm的2个长梁经过20颗M16螺栓联接构成。动力学试验过程如图13所示,在结合部处黏贴2个电阻应变计,电阻应变计的敏感栅长度方向平行于横梁或导轨的长度方向,2个电阻应变计组成半桥,可以消除横梁或导轨受温度等因素的影响,这样测量能够获得较高的测量灵敏度。以数控铣床铣削加工龙门横梁-导轨,用丙酮清洗并吹干结合部。横梁与导轨配对形成螺栓结合部,材料相同皆为45号钢,材料的参数如下:硬度与最初屈服强度之比而成的相关因子K=1, 分形粗糙度 G=1.19×10-9m,结合部两接触材料的弹性模量E′=2.1×1011Pa,结合部两接触材料的当量切变模量G′=8×1010Pa,较软材料的最初屈服强度σy=3.53×109Pa,静摩擦因数f=0.2,作用于整个结合部上的切向交变力幅Q=2×10-8N。锤击之前,在比利时的LMS Test.Lab 9B振动测试和分析系统中设置切向交变力幅的阈值,当锤击力过大时,系统会自动发出人耳明显能听到似碗破“当”的清脆声音。文献[30]提供φ=1.0、E=2.1×1011Pa和σy=3.53×109Pa,与公式φ=σy/E自相矛盾。动荷载是指随时间作急剧变化的荷载。交变力随时间作交替变化。 图12 龙门横梁-导轨测试试件Fig.12 Measure specimen of gantry beam and guideway 图13 试验过程Fig.13 Experimental process 4.1法向预紧力对摩擦能量耗散的影响 图14显示了p对W的影响。 图14 摩擦能量耗散与法向预紧力之间的关系Fig.14 Relation between frictional energy loss and normal preload 4.2分形维数对摩擦能量耗散的影响 图15显示了D对W的影响。 4.3切向力对摩擦能量耗散的影响 当D=1.3时,只改变参数Q,保持其他参数不变,图16表明了Q对W的影响。 4.4分形粗糙度对摩擦能量耗散的影响 只改变参数G,让其他参数不变,图17解释了G对W的影响。 图15 表面粗糙轮廓分形维数对摩擦能量耗散的影响Fig.15 Impact of fractal dimension of a surface harsh profile on frictional energy loss 图16 切向力对摩擦能量耗散的影响Fig.16 Impact of tangential force on frictional energy loss 4.5相关因子对摩擦能量耗散的影响 当D=1.3时,只改变参数K,让其他参数不变,图18揭示了K对W的影响。 4.6单轴向屈服应变对摩擦能量耗散的影响 当D=1.3时,只改变参数σy,因φ=σy/E′,即只改变参数φ,让其他参数不变,图19揭示了φ对W的影响。 4.7静摩擦因数对摩擦能量耗散的影响 当D=1.3时,只改变参数f,让其他参数不变,图20揭示了f对W的影响。 图17 分形粗糙度对摩擦能量耗散的影响Fig.17 Impact of fractal roughness on frictional energy loss 图18 相关因子对摩擦能量耗散的影响Fig.18Impactofrelatingfactoronfrictionalenergyloss图19 单轴向屈服应变对摩擦能量耗散的影响Fig.19Influenceofuniaxialyieldstrainonfrictionalenergyloss图20 静摩擦因数对摩擦能量耗散的影响Fig.20Effectofstaticfrictioncoefficientonfrictionalenergyloss (1) 根据图14,随着法向预紧力的增大,摩擦能量耗散先增大后减小。后半部分结论“摩擦能量耗散随着法向预紧力的增大而减小”与文献[30]论断“平面结合面切向接触阻尼的耗能随着结合面法向载荷的增大而减小”、文献[38]论断“an increase in normal preload causes a decrease in cyclic energy loss”吻合,这是由于结合表面有相应的切向振动,当法向预紧力大时,之后结合表面间的接触状态开始变成完全粗糙度峰点接触状态,实际接触区域增加,相应的幅值减小,消耗的能量少。但文献[30,38]皆未预测出本文前半部分结论“当法向预紧力从0在较窄范围内增大时,摩擦能量耗散迅速从0增加到最大值”,这是由于当法向预紧力接近于0,摩擦能量耗散逼近于0,随着法向预紧力的增大,相应的幅值缓慢减小,但结合表面间的摩擦力很快增大,所以消耗的能量增加很快。 (2) 根据图15(a),当表面粗糙轮廓分形维数为D=1.35~1.4,摩擦能量耗散随着表面粗糙轮廓分形维数的增大而增大。相应地,按照图15(b)~15(c),当表面粗糙轮廓分形维数在D=1.4~1.9,摩擦能量耗散随着表面粗糙轮廓分形维数的增加而减少。 (3) 根据图16,摩擦能量耗散随着切向力的增加而加大,与文献[38]结果“In general, an increase in tangential force causes an increase in cyclic energy loss”相同。 (4) 根据图14和图16,法向预紧力使结合面之间摩擦能量耗散很小,而切向力则耗损较大振动能量(从式(83)也可看出),形成切向阻尼作用[30]。这是由于,实际上当2个粗糙表面相互挤压时,先接触的粗糙峰承受很高的法向力,随后在切向力作用下将发生屈服变形,微凸体横向接触产生的许多能量损失就不能忽略。 (6) 根据图18,摩擦能量耗散随着相关因子的增加而变大。 (7) 根据图19,摩擦能量耗散随着单轴向屈服应变的增加而增大。 (8) 根据图20,摩擦能量耗散随着静摩擦因数的增加而降低,这是因为随着静摩擦因数的增大,根据近代分形几何理论可知法向预紧力越大,微滑趋势将更小,相应的幅值缓慢减小,所以消耗的能量变小。本文结论与文献[32]论断“结合面切向阻尼系数随着结合面之间摩擦因数的增大而增大并趋于恒定”完全相反。静摩擦力等于切向力,与静摩擦因数无关,但最大静摩擦力与静摩擦因数有关[11]。本文结论适用于小载荷。 [1] 田红亮,钟先友,秦红玲,等. 依据各向异性分形几何理论的固定结合部法向接触力学模型[J]. 机械工程学报,2013,49(21):108-122. TIAN Hong-liang, ZHONG Xian-you, QIN Hong-ling, et al. Normal contact mechanics model of fixed joint interface adopting anisotropic fractal geometrical theory[J]. Journal of Mechanical Engineering, 2013,49(21):108-122. [2] 田红亮,钟先友,赵春华,等. 区分弹性与塑性变形的结合面法向校正模型[J]. 机械工程学报,2014,50(17):107-123. TIAN Hong-liang, ZHONG Xian-you, ZHAO Chun-hua, et al. Normal revised model of joint interface distinguishing elastic and plastic deformation[J]. Journal of Mechanical Engineering, 2014,50(17):107-123. [3] 田红亮,钟先友,赵春华,等. 计及弹塑性及硬度随表面深度变化的结合部单次加载模型[J]. 机械工程学报,2015,51(5):90-104. TIAN Hong-liang, ZHONG Xian-you, ZHAO Chun-hua, et al. One loading model of joint interface considering elastoplastic and variation of hardness with surface depth[J]. Journal of Mechanical Engineering, 2015,51(5):90-104. [4] 田红亮,赵春华,朱大林,等. 金属材料结合部法切向刚度修正与实验验证[J]. 农业机械学报,2012,43(6):207-214. TIAN Hong-liang, ZHAO Chun-hua, ZHU Da-lin, et al. Modification of normal and tangential stiffness for joint interface with metallic material and experimental validation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012,43(6):207-214. [5] 田红亮,朱大林,秦红玲,等. 结合部法向载荷解析解修正与定量实验验证[J]. 农业机械学报,2011,42(9):213-218. TIAN Hong-liang, ZHU Da-lin, QIN Hong-ling, et al. Modification of normal load’s analytic solutions for joint interface and quantitative experimental verification[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011,42(9):213-218. [6] 田红亮,赵春华,朱大林,等. 整个螺栓结合部的法向连接动刚度及试验验证[J]. 西安交通大学学报,2012,46(9):31-36. TIAN Hong-liang, ZHAO Chun-hua, ZHU Da-lin, et al. Analysis and validation on normal connection dynamic stiffness of bolted joint interface ensemble[J]. Journal of Xi’an Jiaotong University, 2012,46(9):31-36. [7] 田红亮,朱大林,秦红玲. 固定接触界面法向静弹性刚度[J]. 应用力学学报,2011,28(3):318-322. TIAN Hong-liang, ZHU Da-lin, QIN Hong-ling. Normal static elastic stiffness of fixed contact interface[J]. Chinese Journal of Applied Mechanics, 2011,28(3):318-322. [8] 田红亮,赵春华,方子帆,等. 微动结合部的一次加载过程[J]. 振动与冲击,2014,33(13):40-52. TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. One loading process of fretting joint interface[J]. Journal of Vibration and Shock, 2014,33(13):40-52. [9] 田红亮,赵春华,方子帆,等. 基于各向异性分形理论的结合面切向刚度改进模型[J]. 农业机械学报,2013,44(3):257-266. TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. Improved model of tangential stiffness for joint interface using anisotropic fractal theory[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013,44(3):257-266. [10] 田红亮,方子帆,朱大林,等. 固定接触界面切向静弹性刚度问题研究[J]. 应用力学学报,2011,28(5):458-464. TIAN Hong-liang, FANG Zi-fan, ZHU Da-lin, et al. Investigation on tangential static elastic stiffness of fixed contact interface[J]. Chinese Journal of Applied Mechanics, 2011,28(5):458-464. [11] 田红亮,陈从平,方子帆,等. 应用改进分形几何理论的结合部切向刚度模型[J]. 西安交通大学学报,2014,48(7):46-52. TIAN Hong-liang, CHEN Cong-ping, FANG Zi-fan, et al. Tangential stiffness model for joint interface adopting the revised fractal geometric theory[J]. Journal of Xi’an Jiaotong University, 2014,48(7):46-52. [12] 田红亮,刘芙蓉,方子帆,等. 结合部静摩擦因数修正与定量实验验证[J]. 农业机械学报,2013,44(10):282-293. TIAN Hong-liang, LIU Fu-rong, FANG Zi-fan, et al. Correction of static friction coefficient for joint interface and quantitative test confirmation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013,44(10):282-293. [13] 田红亮,赵春华,方子帆,等. 金属材料表面静摩擦学特性的预测研究——理论模型[J]. 振动与冲击,2013,32(12):40-44,66. TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. Predication investigation on static tribological performance of metallic material surfaces—theoretical model[J]. Journal of Vibration and Shock, 2013,32(12):40-44,66. [14] 田红亮,刘芙蓉,赵春华,等. 金属材料表面静摩擦学特性的预测研究——实验佐证[J]. 振动与冲击,2014,33(1):209-220. TIAN Hong-liang, LIU Fu-rong, ZHAO Chun-hua, et al. Prediction of static friction performance of metallic material surfaces with experimental proof[J]. Journal of Vibration and Shock, 2014,33(1):209-220. [15] 田红亮,赵春华,方子帆,等. 基于各向异性分形几何理论的摩擦非线性数学模型[J]. 振动与冲击,2013,32(23):135-144. TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. Mathematical model of nonlinear friction based on anisotropic fractal geometric theory[J]. Journal of Vibration and Shock, 2013,32(23):135-144. [16] 田红亮,赵春华,方子帆,等. 基于修正分形理论的结合面静摩擦模型[J]. 华中科技大学学报:自然科学版,2013,41(11):71-75. TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. Static frictional model for joint interface using revised fractal theory[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2013,41(11):71-75. [17] 田红亮,朱大林,秦红玲. 结合面静摩擦因数分形模型的建立与仿真[J]. 应用力学学报,2011,28(2):158-162. TIAN Hong-liang, ZHU Da-lin, QIN Hong-ling. Fractal model of static friction coefficient of joint interface and its simulation[J]. Chinese Journal of Applied Mechanics, 2011,28(2):158-162. [18] 田红亮,刘芙蓉,方子帆,等. 引入各向同性虚拟材料的固定结合部模型[J]. 振动工程学报,2013,26(4):561-573. TIAN Hong-liang, LIU Fu-rong, FANG Zi-fan, et al. Immovable joint surface’s model using isotropic virtual material[J]. Journal of Vibration Engineering, 2013,26(4):561-573. [19] Tian Hong-liang, Li Bin, Liu Hong-qi, et al. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools[J]. Elsevier International Journal of Machine Tools & Manufacture, 2011,51(3):239-249. [20] 田红亮,方子帆,赵春华,等. 依据修正GW理论的结合部法向接触研究[J]. 华中科技大学学报:自然科学版,2014,42(6):38-42,47. TIAN Hong-liang, FANG Zi-fan, ZHAO Chun-hua, et al. Normal contact of joint interface using revised GW theory[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014,42(6):38-42,47. [21] 田红亮,赵美云,郑金华,等. 新的柔性结合部法向接触刚度和接触阻尼方程[J]. 西安交通大学学报,2015,49(1):118-126. TIAN Hong-liang, ZHAO Mei-yun, ZHENG Jin-hua, et al. New equations of normal contact stiffness and damping for flexible joint interface[J]. Journal of Xi’an Jiaotong University, 2015,49(1):118-126. [22] 田红亮,郑金华,赵春华,等. 界面损耗因子与法向阻尼的计算方法[J]. 上海交通大学学报,2015,49(5):687-694. TIAN Hong-liang, ZHENG Jin-hua, ZHAO Chun-hua, et al. Calculating method of surface dissipation factor and normal damping[J]. Journal of Shanghai Jiao Tong University, 2015,49(5):687-694. [23] 田红亮,余媛,张屹. 机床支撑地脚结合部法向粗糙接触建模[J]. 浙江大学学报:工学版,2015,49(11):2111-2118. TIAN Hong-liang, YU Yuan, ZHANG Yi. Normal rough contact modeling of machine tool support ground foot joint interface[J]. Journal of Zhejiang University:Engineering Science, 2015,49(11):2111-2118. [24] 田红亮,陈甜敏,郑金华,等. 平行轴圆柱副接触分析[J]. 西安交通大学学报,2016,50(1):8-15. TIAN Hong-liang, CHEN Tian-min, ZHENG Jin-hua, et al. Contact analysis of cylindrical pair with parallel axes[J]. Journal of Xi’an Jiaotong University, 2016,50(1):8-15. [25] 田红亮,郑金华,秦红玲. 舰船艉管水润滑橡胶板条轴承与铜背衬的机械接触力学[J]. 兵工学报,2015,36(12):2369-2380. TIAN Hong-liang, ZHENG Jin-hua, QIN Hong-ling. Mechanical contact mechanics of water lubrication rubber stave bearing and Cu backing for ship stern tube[J]. Acta Armamentarii, 2015,36(12):2369-2380. [26] 田红亮,严峥嵘,郑金华,等. 一个新的干摩擦结合部法向接触阻尼方程[J]. 哈尔滨工业大学学报,2016,48(1):133-140. TIAN Hong-liang, YAN Zheng-rong, ZHENG Jin-hua,et al. A novel expression of normal contact damping for dry tribology joint interface[J]. Journal of Harbin Institute of Technology, 2016,48(1):133-140. [27] 田红亮,余媛,陈甜敏,等. 考虑表面粗糙度和几何曲率的两球体接触问题[J]. 西安交通大学学报,2016,50(3):1-7. TIAN Hong-liang, YU Yuan, CHEN Tian-min, et al. Contact problem between two spheres considering surface roughness and geometrical curvature[J]. Journal of Xi’an Jiaotong University, 2016,50(3):1-7. [28] 田红亮,郑金华,陈甜敏,等. 直线运动滚动导轨副的法向接触力学模型[J]. 西安交通大学学报,2016,50(5):1-11. TIAN Hong-liang, ZHENG Jin-hua, CHEN Tian-min, et al. Normal contact mechanics model of linear motion rolling guideway pair[J]. Journal of Xi’an Jiaotong University, 2016,50(5):1-11. [29] 姚运萍,王智渊. 螺栓连接受载能量损失与结合面参数识别[J]. 中国机械工程,2010,21(16):1941-1943. YAO Yun-ping, WANG Zhi-yuan. Energy dissipation of bolt joint under cycle load and parameter identification of interfaces[J]. China Mechanical Engineering, 2010,21(16):1941-1943. [30] 张学良,温淑花,兰国生,等. 平面结合面切向接触阻尼分形模型及其仿真[J]. 西安交通大学学报,2011,45(5):74-77. ZHANG Xue-liang, WEN Shu-hua, LAN Guo-sheng, et al. Fractal model for tangential contact damping of plane joint interfaces with simulation[J]. Journal of Xi’an Jiaotong University, 2011,45(5):74-77. [31] 张学良,王南山,温淑花,等. 机械结合面切向接触阻尼能量耗散弹塑性分形模型[J]. 机械工程学报,2013,49(12):43-49. ZHANG Xue-liang, WANG Nan-shan, WEN Shu-hua, et al. Elastoplastic fractal model for tangential contact damping energy dissipation of machine joint interfaces[J]. Journal of Mechanical Engineering, 2013,49(12):43-49. [32] 李小彭,王伟,赵米鹊,等. 考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真[J]. 机械工程学报,2012,48(23):46-50. LI Xiao-peng, WANG Wei, ZHAO Mi-que, et al. Fractal prediction model for tangential contact damping of joint surface considering friction factors and its simulation[J]. Journal of Mechanical Engineering, 2012,48(23):46-50. [33] Mindlin R D. Compliance of elastic bodies in contact[J]. Transactions of the ASME Journal of Applied Mechanics, 1949,16(3):259-268. [34] Mindlin R D, Deresiewicz H. Elastic spheres in contact under varying oblique forces[J]. Transactions of the ASME Journal of Applied Mechanics, 1953,20(3):327-344. [35] 同济大学数学系. 高等数学上册[M]. 7版. 北京:高等教育出版社,2015:148,224-228. [36] 同济大学数学系. 高等数学下册[M]. 7版. 北京:高等教育出版社,2015:287-289. [37] Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. Transactions of the ASME Journal of Tribology, 1991,113(1):1-11. [38] Padmanabhan K K. Prediction of damping in machined joints[J]. Elsevier International Journal of Machine Tools & Manufacture, 1992,32(3):305-314. [39] Zhang Xue-liang, Wang Nan-shan, Lan Guo-sheng, et al. Tangential damping and its dissipation factor models of joint interfaces based on fractal theory with simulations[J]. Transactions of the ASME Journal of Tribology, 2014,136(1):011704-1-011704-10. Frictional energy loss mechanism of bolt joint interface in machine tools considering transverse loading-unloading-oscillating strong interaction TIAN Hongliang, YU Yuan, ZHANG Yi, CHEN Tianmin, ZHENG Jinhua (College of Mechanical and Power Engineering, China Three Gorges University, Yichang 443002, China) When a normal force acting on an asperity kept constant, the tangential loading, tangential unloading and tangential oscillating contact equations between tangential force and deformation were deduced in detail. The mechanical model for shear contact frictional energy dissipation per cycle was built when two spherical asperities contacted. Based on Hertz static elastic normal contact theory, the curvature radius of the asperity’s top was derived. Owing to the smooth and continuous properties of normal force of microcontact, the mathematical expressions about critical elastic deformation micro-contact area and critical deformation were modified. Facing the equations with conditions and based on elastic and purely plastic deformation, the theoretical models for bolt joint interface normal force and transverse contact frictional energy dissipation were established. A gantry beam-rail bolt joint interface was taken as a study object in the Linear MC6000 Plano pentahedral machining center driven by a linear motor of Beijing Machine and Electricity Institute High-Tech Company Limited. The influence laws of normal preload, fractal dimension of a surface harsh profile, tangential force, fractal roughness, related factor, uniaxial yield strain and static friction coefficient on the transverse contact frictional energy dissipation were analyzed. Furthermore, the visual numerical analysis results showed that the transverse contact frictional energy dissipation firstly increases and then diminishes with increase in normal preload; the transverse contact frictional energy dissipation increases with increase in the fractal dimension or fractal roughness of a surface rough profile in the smaller range of the fractal dimension of the surface rough profile; the transverse contact frictional energy dissipation decreases with increase in the fractal dimension or fractal roughness of a surface rough profile in the larger range of fractal dimension of the surface rough profile; the transverse contact frictional energy dissipation increases with increase in tangential force, related factor and uniaxial yield strain; that the transverse contact frictional energy dissipation decreases with increase in static friction coefficient is completely opposite to the classical conclusion, this is because that when the static friction coefficient becomes larger, the normal preload becomes higher based on the neoteric fractal geometric theory, and the tendency of microslip becomes much smaller, so the transverse contact frictional energy dissipation becomes smaller. transverse loading; transverse unloading; transverse oscillating; machine tools; bolt joint interface; normal preload; transverse fluctuation force; frictional energy 国家自然科学基金面上资助项目(51275273);2016年三峡大学研究生科研创新基金项目(SDYC2016033) 2015-09-06修改稿收到日期:2016-02-22 田红亮 男,博士,副教授,1973年6月生 张屹 男,博士,教授,博士生导师,1976年12月生 TH113.1 A 10.13465/j.cnki.jvs.2016.15.011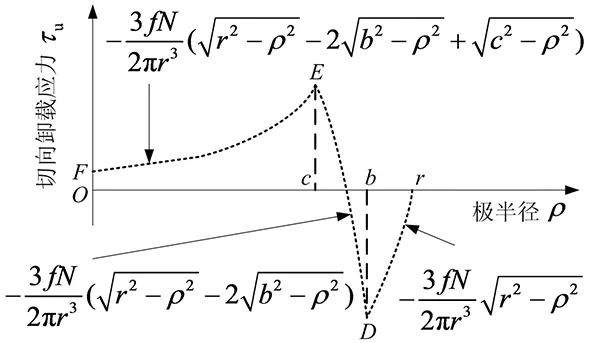
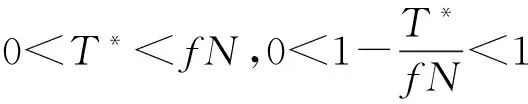







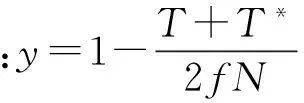

2 分形几何理论的校正

3 整体结合部的摩擦能量耗散
4 机床螺栓结合部摩擦能量耗散之算例



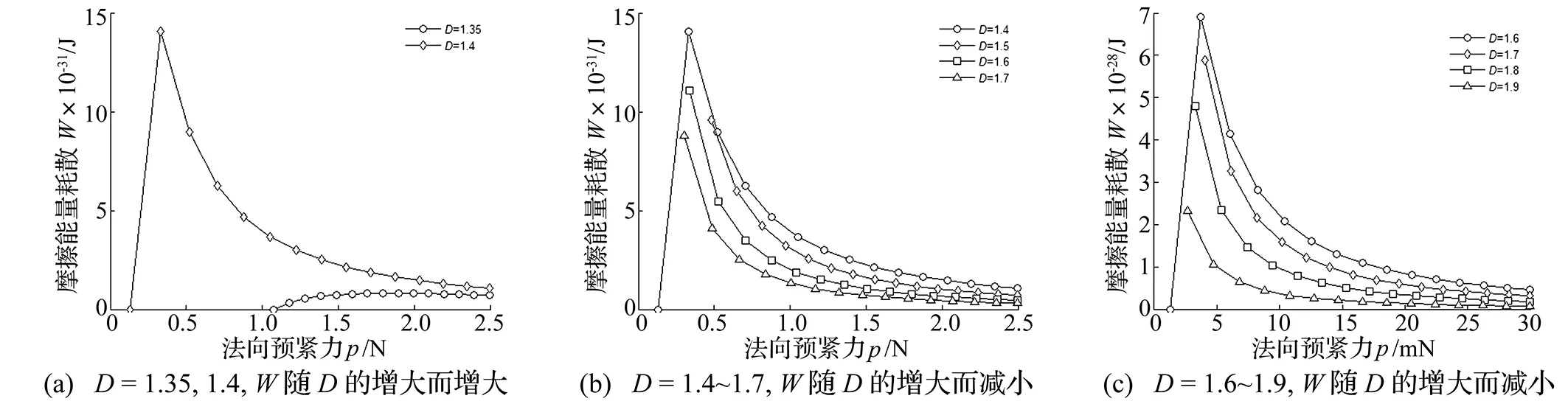
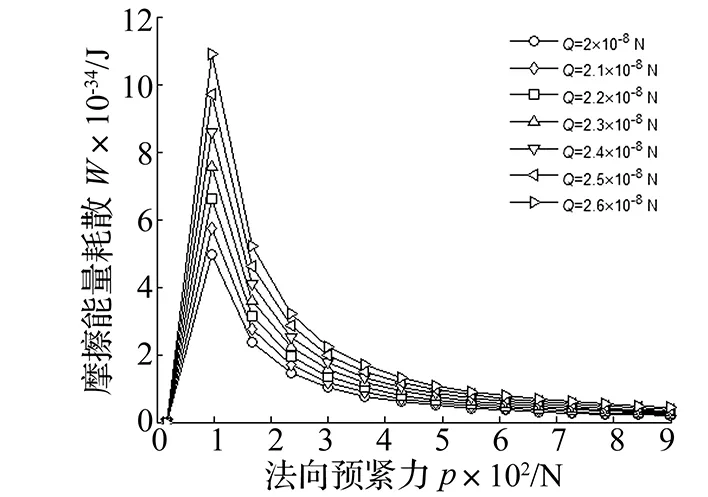


5 结 论

