多通道增强的干涉仪测向方法

李维科，韩田田，汤四龙，樊　荣，万　群

(1.中国电子科技集团公司 航空电子信息系统技术重点实验室，成都　610036；2.电子科技大学 电子工程学院，成都　611731； 3.同方电子科技有限公司， 江西 九江　332007)



多通道增强的干涉仪测向方法

李维科1，韩田田2，汤四龙3，樊荣1，万群2

(1.中国电子科技集团公司 航空电子信息系统技术重点实验室，成都610036；2.电子科技大学 电子工程学院，成都611731； 3.同方电子科技有限公司， 江西 九江332007)

针对干涉仪测向性能受多通道相位不一致性影响特别严重的问题，提出了一种多通道增强干涉仪测向方法，利用未校正的多通道信号辅助部分校正后的通道信号进行干涉仪测向；仿真实验结果表明：与仅利用校正后的双通道干涉仪测向方法相比，提出的相位不一致的多通道增强的干涉仪测向方法具有更高的测向精度。

干涉仪测向；相位不一致；多通道增强本文引用格式：李维科，韩田田，汤四龙，等.多通道增强的干涉仪测向方法[J].兵器装备工程学报，2016(8):98-100.

经过多年的大量研究，出现了许多各具特色的测向算法，特别是干涉仪测向方法，由于具有高精度、高灵敏度、抗干扰性强、工作频率覆盖范围广等特点，在无线电测监测领域受到了极高的关注[1]。但是实际中，当阵列的接收通道间存在相位不一致性时，会恶化干涉仪的测向效果，无法得到有效的DOA估计，限制了其在实际中的应用[2]。因此人们特别关注通道相位误差的校正问题[3]。

针对阵列误差中的通道幅相误差，A.J.Weiss 和B.Friedlander[3]提出的方法可在估计信号来波方向的同时对各阵元的通道幅相误差进行校正，但该方法必须满足一定的收敛条件且对通道幅相误差大小有要求。文献[4]提出的一种盲校正方法要求入射信号服从非高斯分布，限制了该方法的应用。文献[5]运用阵列协方差矩阵的Toeplitz结构对通道幅相误差进行估计，该方法使用了阵列协方差矩阵的上三角矩阵中所有对角线信息，运算量较大[6]。

本文提出一种多通道增强干涉仪测向方法，该方法同样使用全部的阵元信号信息，但是并不需要对全部的信号均进行相位误差校正，无需特征分解，运算量小，且无迭代操作，不存在收敛问题[7]，减少了校正时间，也降低了对通道相位一致性的要求。

1　通道的幅相误差模型

设阵列信号的接收通道中，第i个通道的幅相误差为

(1)

式(1)中，αi为通道i的幅度误差，φi为通道i的相位误差。理想情况下αi=1，φi=0，那么阵列的接收信号模型为

Y=GAS+N

(2)

其中，G为通道幅相误差矩阵：

diag(·)为对角矩阵符号，αi是幅度误差参数，φi是相位误差参数。M为阵元数，A为信号的方向矩阵，S为信号的数据矩阵，Y为通道接收到的信号矩阵，N为噪声矩阵，假定各个通道之间的噪声是相互独立的高斯白噪声。对于不同的发射源信号以及不同的天线阵元位置，接收信号中的αi和φi不同。

下面先介绍多通道增强的干涉仪测向原理，再利用仿真实验验证其有效性，最后给出结论。

2　多通道增强的干涉仪测向原理

如图1所示，M阵元均匀线阵，阵元间距为d，将阵元0作为参考阵元，其余阵元与阵元0组成的基线长度分别为d0i=id,i=1,2,…,M-1，每个阵元对应一个信号的接收通道，有一远场窄带信号源s(n)入射到阵列上，入射角为θ，信号波长为λ，则入射信号的方向向量为

(3)

其中k=2πdsinθ/λ。

图1　M元均匀线阵

根据式(2)的接收信号模型，可得图1阵列的入射信号模型为[3]

(4)

其中

vi(n)服从独立同分布的高斯噪声。

选择任意两通道，对其通道幅相误差进行校正。假设选择的两通道编号为p,q，其校正后的幅相误差参数αp=1,φp=0，αq=1,φq=0，两通道的幅相特性一致，设校正后幅相误差矩阵为Ga。下面利用两通道的输出信号与阵列输出的所有信号对信号的方位角进行估计：

首先，计算互相关：

(5)

(6)

其中N为信号的快拍数。

然后，利用式(5)和式(6)可得：

(7)

最后，利用r得到信号的来波方向估计：

(8)

在上面的求解过程中，使用了全部通道的信号，但是仅需对其中的两个通道p,q进行了误差校正即可实现有效的方位角估计。

3　仿真验证

由式(5)或式(6)可直接求得p和q通道的互相关为

(9)

得到信号来波方向估计

(10)

下面我们对本论文中提出的多通道增强的干涉仪测向法进行仿真验证。

式(8)中使用相位差r对方向进行估计，r使用了所有阵元信号的信息，式(10)中使用相位差rpq对方向进行估计，rpq仅使用了校正后的两通道信号，下面比较式(8)多通道增强的干涉仪测向方法和式(10)双通道干涉仪测向方法的测向结果。

如图2所示，仿真中采用9阵元均匀线阵，阵元间距为λ/2，每个阵元对应一个接收通道，不考虑通道的幅度误差，通道的相位误差服从[0,2π]的均匀分布，信号入射角为34.3°，快拍数为64，最后两个通道的相位误差为

改变信噪比，由式(8)和式(10)求得两种相位差估计的角度，并分析角度误差。

分析图2可知，在相同信噪比下，由式(8)所得的角度估计的均方根误差要小于由式(10)所得的角度估计的均方根误差，式(8)中用于估计角度的相位差r由所有的通道信号获得，该种方法获得的相位差测量精度要高于式(10)中的直接法。多通道增强的干涉仪测向法综合利用了所有通道信号，提高了相位差的测量精度，进而提高了测角精度。

图3给出了不同阵元数对干涉仪测向误差的影响，仿真条件与图2相同，信噪比为-2 dB。分析可知，由于式(10)双通道干涉仪测向方法仅利用校正后的两个通道信号，因此改变阵列数并不会影响其测向精度。相比较而言，由于式(8)多通道增强的干涉仪测向方法采用式(7)求得的相位差进行角度估计，利用了全部阵元的信号，增加阵元数可以有效改善其测向精度，但是却无需增加校正时间和成本，仅对其中的两个通道信号进行校正。

图4给出了不同信号快拍数对干涉仪测向误差的影响，仿真条件与图2相同，但是信噪比为-2 dB，阵元数为9。分析图4可知，增加信号的快拍数(由16增加到32、64、128、256、512)，两种方法的测向精度均得到提高。在快拍数相同的情况下，式(8)多通道增强的干涉仪测向精度更高。

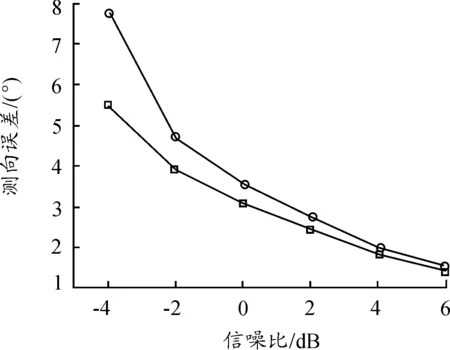
图2　不同信噪比情况下测向误差的比较

图3　不同阵元数情况下测向误差的比较

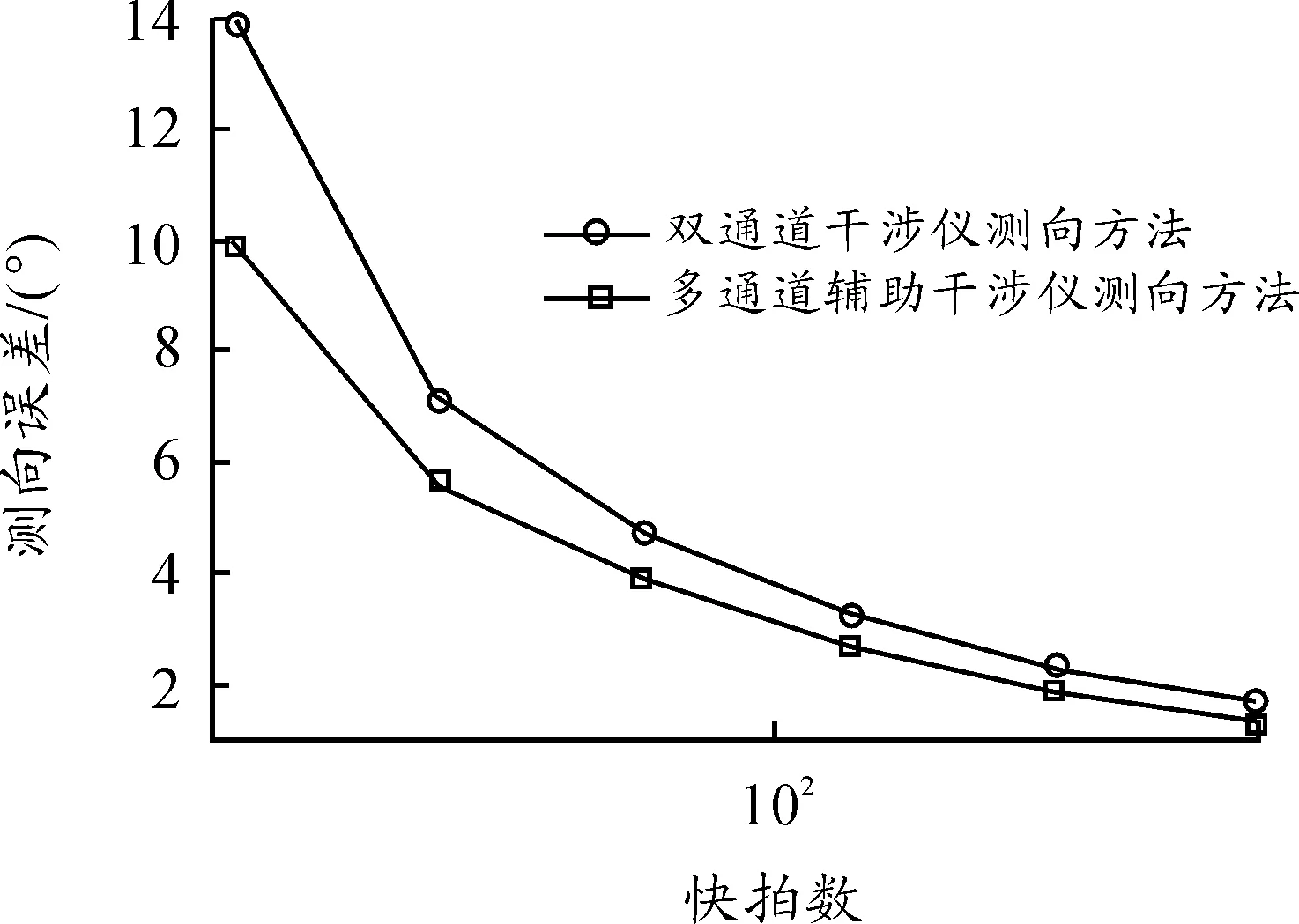
图4　不同快拍数情况下测向误差的比较

4　结论

针对通道相位误差影响干涉仪测向性能的问题，本文提出了一种多通道增强的干涉仪测向法，使用未校正过的信号进行辅助测向与仅使用部分校正后的信号进行测向相比较，辅助测向法具有更高的测向精度和稳健性。在不同信噪比、阵元数和快拍数等情况下进行的仿真实验验证了该结论的正确性。

[1]李晓星，王磊.一种基于五元圆阵的星载相位干涉仪定位求解法[J].四川兵工学报，2015(2):41-43.

[2]CAO S,YE Z,XU D,et al.A Hadamard Product Based Method for DOA Estimation and Gain-Phase Error Calibration[J].IEEE Transactions on Aerospace & Electronic Systems,2013,49(49):1224-1233.

[3]WEISS A J,FRIEDLANDER B.Eigenstructure methods for direction finding with sensor gain and phase uncertainties[J].Circuits Systems & Signal Processing,1990,9(3):271-300.

[4]KIM J,YANG H J,JUNG B W,et al.Blind Calibration for a Linear Array With Gain and Phase Error Using Independent Component Analysis[J].IEEE Antennas and Wireless Propagation Letters,2010,9(1):1259-1262.

[5]PAULRAJ A,KAILATH T.Direction of arrival estimation by eigenstructure methods with unknown sensor gain and phase[C].IEEE International Conference on Acoustics,Speech,and Signal Processing,1985:640-643.

[6]何子述.现代数字信号处理及其应用[M].北京：清华大学出版社，2009：75-120.

[7]陈晓威，李彦志，张国毅.干涉仪测LFM信号方向误差分析[J].四川兵工学报，2015(8):119-123.

(责任编辑周江川)

Interferometer Direction Finder Enhanced by Multi-Channel

LI Wei-ke1, HAN Tian-tian2, TANG Si-long3，FAN Rong1， WAN Qun2

(1.Key Laboratory of Avionic Information System Technology,China Electronics Technology Group Corporation, Chengdu 610036, China;2.School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China;3.Tongfang Electronic Science and Technology Co., Ltd., Jiujiang 332007, China)

To solve the problem of inconsistency of multiple channels phase response, which has serious effect on the performance interference direction finder, this paper presented a multi-channel aided interferometer direction finding method. It was aided by multi-channel with phase inconsistency and exploited both the uncorrected multi-channel signals and corrected multi-channel signals to perform interference direction finding. The simulation results show that the proposed interferometer direction finder using multi-channel with phase inconsistency has higher accuracy of direction findingcompared with the direction finding method using only two channel interferomete.

interferometer direction finding; phase inconsistency; aided by multi-channel

2016-02-17；

2016-03-15

国家自然科学基金(61172140)

李维科(1980—)，男，工程师，主要从事通信信号处理与雷达信号分选研究。

10.11809/scbgxb2016.08.022

format:LI Wei-ke, HAN Tian-tian, TANG Si-long，et al.Interferometer Direction Finder Enhanced by Multi-Channel[J].Journal of Ordnance Equipment Engineering,2016(8):98-100.

TN957

A

2096-2304(2016)08-0098-03

【信息科学与控制工程】