利用静压数据探讨渤海海域常压油藏砂体连通性

钱　赓，张建民，刘传奇，张　岚，杨海风，穆鹏飞，李兴丽

[中海石油(中国)有限公司 天津分公司，天津 300450]



利用静压数据探讨渤海海域常压油藏砂体连通性

钱赓，张建民，刘传奇，张岚，杨海风，穆鹏飞，李兴丽

[中海石油(中国)有限公司 天津分公司，天津 300450]

基于同一个油藏压力系统的一致性，常压条件下地层压力与海拔理论上的线性关系是目前判断同一层序地层格架下砂体连通关系的重要依据。受储层高渗与流体非均质性的影响，判断砂体连通性的线性规律存在局限。通过数学归纳分析，发现常压油藏砂体连通关系的新方法，即建立压力系数与海拔的反比例函数关系。根据反比例函数的相交性、单调性、有界性与对称性，探讨反比例函数性质与油藏压力系统的关系，进一步判断砂体的连通性。针对渤海海域7个油田、50余个开发井已证实连通关系的常压油藏，验证压力系数-海拔反比例函数性质与砂体连通性的关系并证实：①函数图像连续且相交重合、单调性与渐近线一致且对称轴唯一是判断同一层序地层格架下砂体相连通的关键依据；②压力系数对分析砂体的连通关系比地层压力的线性关系更为敏感、可靠；③函数曲率受储层渗透性和流体性质等影响，规避了线性规律的局限。

压力系数；反比例函数；流体非均质性；渗透性；常压油藏；渤海海域

1　砂体连通性研究现状

砂体连通性常用分析技术有钻井小层对比、测井曲线特征对比、储层地质建模技术和单属性描述等[1]，受海域范围钻井较少、储层物性非均质性、地震资料多解性等因素影响，上述方法应用受到一定限制。依据同一个油藏具有统一的压力系统，不同的油藏具有不同的压力系统，利用地层压力判断砂体连通关系在国内外诸多油田已经得到了广泛应用[2]。

李传亮(2005)阐述了利用地层压力的线性关系判断砂体连通关系的基本原理：同一个油藏任意一点的折算(等效)压力都相等，即一个连通性油藏测点压力位于同一条直线，且压力折算到基准面上的值是唯一的[3]。

Shaker(2001)提出利用流体剩余压力与封存压力定量-半定量分析砂体连通关系[4-6]。流体剩余压力是在油藏深度剖面中地层压力与区域性静水压力的差值。封存压力是受泥岩夹层所分割的两套储层的压力差值，代表泥岩夹层的封闭能力(图1)。连通性油藏流体剩余压力相同，不存在封存压力。

(1)

(2)

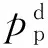
受储层高渗及流体非均质性导致油藏顶部地层压力数据“异常”、非同相流体剩余压力不同(图1)、压力数据 “分辨率不高”的影响，在实际应用中出现砂体连通关系判断“不准”的现象，地层压力-海拔的线性关系不足以作为决定砂体连通性的关键证据。

总结国内外诸多学者关于油藏压力与砂体连通关系的认识，通过数学归纳分析利用电缆地层测试器在渤海海域7个油田、50余个常压油藏取得的1 000个实测地层压力数据[7-10]，提出利用压力系数-海拔的反比例函数关系判断砂体连通关系的方法，以期提高连通性分析的把握程度，为油田合理勘探开发提供关键依据。

图1　油藏流体剩余压力与封存压力示意图[4-6]Fig.1　Schematic diagram showing residual pressure and sealing pressure of reservoirs[4-6]

2　反比例函数性质与连通性

根据流体力学理论，一个常压油藏中任意点的实测地层压力满足压力方程，即一个油藏地层压力与海拔理论上满足线性关系(图2a)，地层压力随海拔增加而线性递增[11-14]，如下关系式：

(3)

而另外一种分析地层压力随海拔变化规律的方法——压力系数——很重要但常又被忽略。假设地层水密度恒定，经过公式推导：

(4)

(5)

(6)

式中：H为海拔，m；ρw为地层水密度，g/cm3；αp为压力系数，无量纲；a，b，c为常数。

上式是以压力系数αp为自变量、海拔H为因变量的反比例函数的变体(图2b)，其原函数为y=1/x(x>0，y<0)，具有相交性、单调性、有界性和对称性4个基本性质[15]。利用油藏压力系数-海拔反比例函数性质探讨其油藏意义与压力系统的关系、判断同一层序地层格架下砂体的连通关系。

1) 相交性

反比例函数图像相交重合，油藏具有统一的压力系统，反之亦然。理论上公式(6)中b和c值相等的反比例函数图像重合，b和c值不相等的反比例函数图像永不相交。根据反比例函数的相交性，同一个油藏压力系数能够拟合到一条反比例函数曲线上，非同一个油藏则不能。

2) 单调性

随着油藏海拔变浅，压力系数呈现单调递增趋势(图2b)。受重力分异作用控制，常压油藏流体按密度分异且连续变化。在油藏高部位，因存在气顶或油层溶解气含量偏高，流体密度与粘度偏低，与油藏构造深度正相关，其地层压力高于其折算压力(图2a)。在油水过渡带，随含水饱和度增加，流体密度趋近地层水密度，地层压力趋近静水压力，压力系数逐渐接近常数。压力系数的单调性是油藏流体性质随油藏深度连续变化的结果。

函数单调性决定其曲率连续规律变化，油柱高度、流体性质和储层物性均影响反比函数曲率变化，且不同海拔主控因素不同。Selim Simon Shaker(2014)指出浅层油藏反比例函数曲率受储层渗透性影响，且满足达西定律Q=-K/μ*Δp，即在流量与流体粘度一定的情况下，地层压力变化率与渗透率满足反比关系[4]，因此在浅层高渗储层反比例函数曲率变化较小(图3；表1)。而在中、深层中-低渗油藏压力变化主要受流体密度影响，函数曲率变化相对较大(图2b)。

图2　油藏压力-海拔数学模型Fig.2　Mathematical model of reservoir pressure-elevation below sea levela.地层压力-海拔线性函数分布；b.压力系数-海拔反比例函数分布

3)有界性

压力系数-海拔反比例函数存在两条渐近线(αp=1/c，H=h)，同一油藏压力系数与油藏高度的数值分布受两条渐近线控制，渐近线不一致的两套砂体不属于同一压力系统。随油藏海拔变浅，压力系数单调递增并无限接近于油藏顶部破裂压力，海拔的上限值同样趋近于最大油藏高度h。海拔增加，地层压力逐渐偏向静水压力，压力系数的下限值也无限趋近于静水压力系数1/c(图2b)。

4)对称性

反比例函数图像是轴对称图形，且对称轴唯一；连通性油藏压力系数对称轴唯一，对称轴不唯一的两套或多套砂体不属于同一个压力系统，不具有连通关系。

图3　渤海南部KL16-X井馆陶组 高渗油藏压力系数-海拔剖面Fig.3　Profile of pressure coefficient vs. elevation of the Guantao Formation high permeable reservoirs of Well KL16-X in the southern Bohai Sea

在气顶压力、底水或边水浮力等油藏驱动力的直接控制下，油藏压力保持动态平衡状态-压力系数随海拔深度的反比例函数分布。不同油藏的油柱高度、流体性质、储层物性等均存在差异，油藏压力平衡条件不同，使反比例函数的性质及意义成为判断砂体连通关系的关键要素。

3　应用与验证

BZ28-X油田位于渤海南部海域黄河口凹陷中央构造脊，产层为新近系明化镇组下段[16]。1井、3井和4井在该层系均钻遇两套稳定且上下叠置砂体(图4)，沉积相类型为河道型浅水三角洲，储层高孔、高渗特征明显，孔隙度分布范围为26.6%～34.8%、渗透率分布范围为(148.5～3 151.7)×103 μm2。

开发井在1#和2#砂体钻遇了不同的油水界面，两套砂体不具有连通关系。对比4井1#砂体与1井和3井2#砂体，压力数据分布在两条近平行的直线，反比

表1　渤海南部KL16-X井馆陶组砂体地层压力数据及 物性统计Table 1　Pressure and physical properties of sand bodies of the Guantao Formation of Well KL16-X in the southern Bohai Sea

注：孔隙度与渗透率均为测井解释与储层厚度的加权平均值。

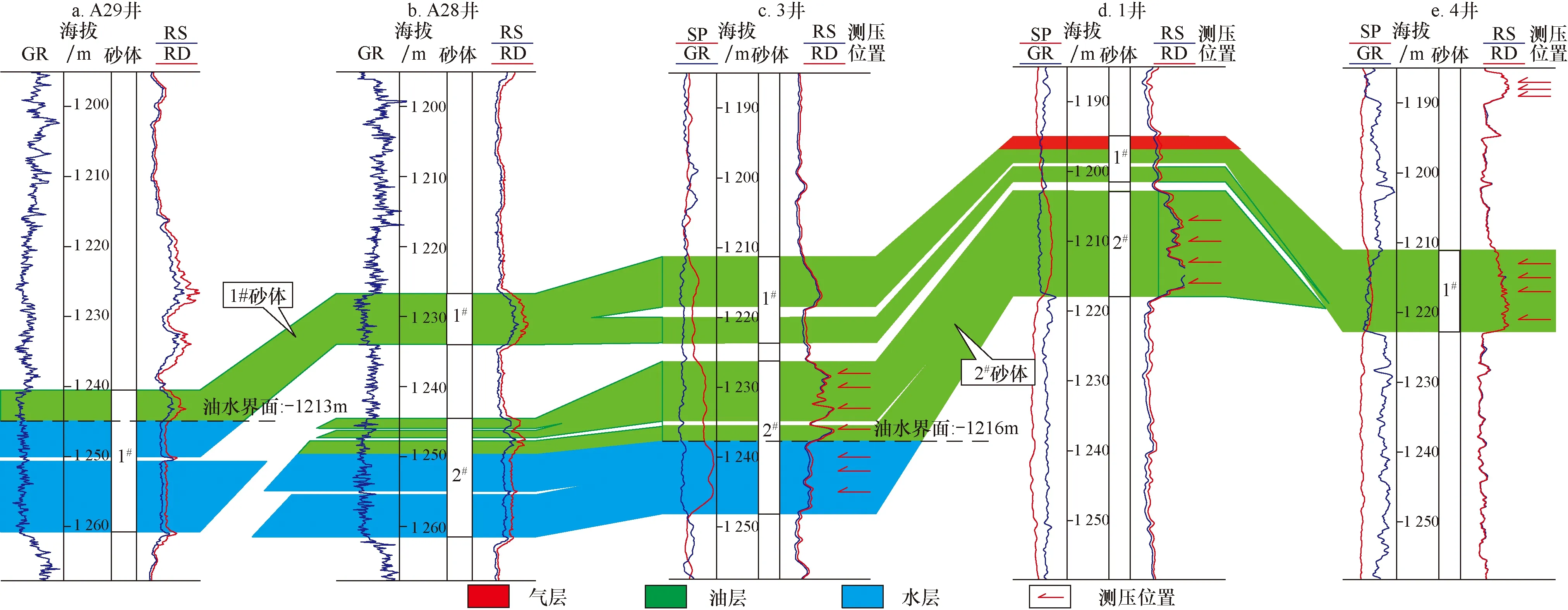
图4　渤海南部BZ28-X油田明下段1#和2#砂体连井对比剖面Fig.4　Cross-well correlation of sandbodies 1# & 2# in the Lower Minghuazhen Formation in BZ28-X oilfield,the southern Bohai Sea

例函数图像不能相交重合、压力系数不具有单调性与相同的渐近线、函数图象对称轴也不同(图5；表2)，两套砂体不属于统一的压力系统。

开发井证实2#砂体内部连通，1井和3井钻遇的2#砂体地层压力数据均分布于一条直线，地层压力系数共同拟合为一条反比例函数曲线(图5b；表2)，函数形态属于反比例函数的下半部分。反比例函数图像相交重合、压力系数单调性分布且函数曲率继承性变化、可以具有共同的渐近线与对称轴，两套砂体压力系统一致，证实了反比函数性质及油藏意义可以作为判断砂体连通关系的关键依据。

图5　渤海南部BZ28-X油田明下段1#和2#砂体 地层压力/压力系数-深度剖面Fig.5　Formation pressure/pressure coefficient vs.depth of sandbodies 1# & 2# in the Lower Minghuazhen Formation in BZ28-X oilfield,the southern Bohai Seaa.地层压力-海拔线性函数分布；b.压力系数-海拔反比例函数分布

JZ25-X油田位于辽东湾海域西部的辽西低凸起中部[17-18]。井距仅为1km的3井和5井在古近系沙河街组三段钻遇两套同期发育砂体，沉积相类型为扇三角洲前缘沉积，地震上同相轴连续稳定而且两套砂体油层可以拟合为同一条直线上，综合沉积储层、地震资料认为两套砂体具有连通关系(图6，图7a；表3)。但是，目前的开发井已经在两井区钻遇了不同的油水界面，证实两套砂体不连通。

表2　渤海南部BZ28-X油田明下段1#和2#砂体地层压力、 压力系数与含油气性Table 2　Formation Pressures,pressure coefficient,and hydrocarbon contents of the Neogene sandbodies 1# & 2#in the Lower Minghuazhen Formation in BZ28-X oilfield, the southern Bohai Sea

从反比函数的性质及油藏意义的角度去探讨3井、5井钻遇的两套砂体的连通关系。首先，压力系数不能拟合为同一条反比例函数曲线，即函数图像不能相交重合。其次，5井砂体压力系数与海拔的下/上限值已经开始趋近于静水压力常数与油藏高度固定，函数曲线具有明显的渐近线，而3井砂体压力系数曲线的渐近线与之不同、函数曲率也存在突变。最后，5井砂体压力系数对称性较好，与3井对称轴不一致。综合认为3井、5井沙三段钻遇两套同期砂体属于两个油藏单元，彼此不连通。压力系数对于判断砂体连通关系更为真实。

4　反比例函数的优势

4.1提升高渗储层连通性分辨能力

地层压力与海拔的线性关系为砂体连通关系的确定提供了十分重要的依据，但是在浅层高渗储层存在分辨能力不足的问题。根据达西定律，压力变化率与渗透率的反比关系决定了非连通高渗砂体间流体剩余压力相差很小、泥岩夹层封存压力很低，线性关系不足以成为浅层高渗储层连通性分析的关键证据。而压力系数—海拔变化规律的认识，把传统的线性关系转化为分辨率更高的反比例函数，提高了高渗砂体连通关系判断的可靠性。

KL9-X井在浅层明化镇组钻遇两套相邻河流相砂体[19]，测井解释渗透率分别2 913.7×10-3和575.1×10-3μm2(表4)，区域研究表明两套砂体具有“一砂一藏”的成藏特征，彼此不具有连通关系。两套砂体压力梯度分别为1.24和1.25 psi/m，封闭压力仅1.6 psi(图8a)，非连通的证据不足。

图6　渤海辽东湾JZ25-X油田3井和5井古近系沙三段砂体连井对比Fig.6　Cross-well correlation of the sandbodies in the third member of the Paleogene Shahejie Formation in Well 3 & 5 of JZ25-X oilfied,Liaodongwan offshore of the Bohai Sea

图7　渤海辽东湾JZ25-X油田3井和5井古近系沙三段砂体地层压力/压力系数-深度剖面Fig.7　Formation pressure/pressure coefficient vs. depth of the sandbodies in the third member of the Paleogene Shahejie Formation in Well 3 & 5 of JZ25-X oilfield,Liaodongwan offshore of the Bohai Seaa.地层压力—海拔线性函数分布；b.压力系数—海拔反比例函数分布表3　渤海辽东湾JZ25-X油田古近系沙三段砂体 地层压力数据Table 3　Pore pressure and pressure coefficient of the third member of the Paleogene Shahejie Formation in JZ25-X oilfield,Liaodongwan offshore of the Bohai Sea

井号海拔/m地层压力/psi压力系数3-2116.53175.41.05581-2121.53180.61.05505-2125.53184.91.05449-2130.53190.61.05389-2136.53197.11.05307-2142.53203.91.05236-2146.03207.41.05179-2150.53212.21.05116-2152.53214.41.050905-2325.53399.71.02880-2330.23403.81.02796-2336.03410.01.02728-2337.03411.21.02720-2343.53419.01.02669-2345.03421.11.02667-2347.03423.91.02663-2357.03437.31.02628-2359.03440.11.02624-2362.03444.61.02628

利用压力系数-海拔反比例函数性质可知：①两套砂体压力系数不能相交重合，无法拟合为同一个反比例函数曲线；②1#砂体函数形态较为完整，压力系数与海拔深度均已开始趋近于两条渐近线，而2#砂体未见其上下限；③两套砂体函数曲率不具有连续性变化；④1#砂体反比例函数图像的对称轴与2#砂体不一致(图8b)。综合判断，两套砂体不具有连通关系，压力系数—海拔的反比例函数关系对分析砂体的连通关系比线性关系更为敏感、可靠。

4.2排除连通性分析中的干扰

根据水静力学理论，地层压力-海拔线性关系判断砂体连通关系仅适用于同种性质流体，必须排除流体非均质性的影响；而压力系数的反比例函数分布是在气顶压力、底水或边水浮力等油藏驱动力的动态平衡状态下产生的，其形态的变化受油柱高度、流体性质、储层物性等因素控制，规避了储层高渗与流体非均质性对线性关系的干扰。KL9-X井1#砂体的第一个测压点测井解释为气层，其余均为油层。受气顶压力及不同流体性质影响，4个测压点并不满足地层压力线性规律，而排出干扰因素的地层压力线性规律明显。非均质性在反比例函数中转化为对其函数形态的控制(图8)。

5　结论

1) 压力系数-海拔反比例函数性质及油藏意义是探讨常压地层砂体连通性关系的新方法，其判断标准是：反比例函数图像连续且相交重合、单调性与渐近线一致且对称轴唯一。

图8　渤海南部KL9-X井明下段1#和2#砂体地层压力/压力系数-深度剖面Fig.8　Formation pressure/pressure coefficient vs. depth of sandbodies 1# & 2# in the Lower Minghuazhen Formation of Well KL9-X, the southern Bohai Seaa.地层压力-海拔线性函数分布；b.压力系数-海拔反比例函数分布表4　渤海南部KL9-X井明化镇组砂体地层 压力与含油气性统计Table 4　Pressures,permeability and hydrocarbon contents of the Neogene Minghuazhen Formation in Well KL9-X, the southern Bohai Sea

砂体海拔/m地层压力/psi压力系数平均渗透率/(×10-3μm2)测井解释1#-1133.01623.41.02758-1140.01624.91.02209-1142.01627.41.02184-1144.01629.91.021552913.7气层油层油层油层2#-1159.61651.11.02069-1161.01652.91.02051-1162.01654.11.02039575.1油层油层油层

注：孔隙度与渗透率均为测井解释与储层厚度的加权平均值。

2) 相比地层压力-海拔线性关系，压力系数-海拔反比例函数变化规律对分析同一层序地层格架中砂体连通性更加可靠。

3) 渤海海域常压油藏压力系数反比例函数曲率受油柱高度、流体性质、储层物性等因素控制，规避了储层高渗与流体非均质性对地层压力线性关系的干扰。

[1]刘传奇,吕丁友,侯冬梅.渤海A油田砂体连通性研究[J].石油物探,2008,47(3):251-255.

Liu Chuanqi,Lv Dingyou,Hou Dongmei.Study of connectivity of sand bodies in oilfield A,Bohai area[J].Geophysical Prospecting for Petroleum,2008,47(3):251-255.

[2]Mark D.Zoback.Reservoir geomechanics[M].New York：Cambridge University Press,2007：3-55.

[3]李传亮.油藏工程原理[M].北京：石油工业出版社,2005,11：5-7.

Li Chuanliang.Fundamentals of reservoir engineering[M].Beijing：Petroleum Industry Press,2005,11：5-7.

[4]Selim Simon Shaker.Reservoir vs.seal pressure gradients:Calculations and pitfalls[C]// American Association of Petroleum Geologists，AAPG 2014 Annual Convention & Exhibition.Houston:Omnipress，2014:1834685.

[5]Selim Simon Shaker.Geopressure compartmentalization in Keathley Canyon deep water,Gulf of Mexico[J].Comparative Drama,2005,39(2):131-156.

[6]Leonardo Enrique Aguilera Gomez,Francisco Espitia Hernandez,Devendra Kumar,et al.Understanding pressure compartmentalization in Ultra deep-water drilling off Mexican Gulf Coast:A case study[C].// American Association of Petroleum Geologists,AAPG 2014 Annual Convention & Exhibition,Houston:Omnipress.2014:1841804.

[7]潘福熙.ERCT电缆地层测试器应用实例研究[J].国外测井技术,2012(4):45-48.

Pan Fuxi.Research of the ERCT wireline formation tester application[J].World Well Logging Technology,2012,(4):45-48.

[8]马建国,符仲金.电缆地层测试器原理及其应用[M].北京：石油工业出版社,1995:1-174.

Ma Jianguo,Fu Zhongjin.Principles and applications of wireline formation tester[M].Beijing：Petroleum Industry Press,1995：1-174.

[9]陈永生,谭廷栋.地层压力理论与评价-压力计算参考书[M].北京：石油工业出版社,1990:1-157.

Chen Yongsheng,Tan Tingdong.The pressure log reference manual-Theory and evaluation of formation pressure[M].Beijing：Petroleum Industry Press,1990:1-157.

[10]王昌学,曹文利,王向荣.电缆地层测试压力梯度的计算与应用[J].石油勘探与开发,2008,35(4):476-481.

Wang Changxue,Cao Wenli,Wang Xiangrong.Pressure gradient computation and application of wireline formation tester[J].Petroleum Exploration and Development,2008,35(4):476-481.

[11]匡立春.电缆地层测试资料应用导论[M].北京:石油工业出版社，2005:1-140.

Kuang Lichun.An introduction to applied of the wireline formation data[M].Beijing:Petroleum Industry Press,2005:1-140.

[12]匡立春,毛志强,孙中春,等.基于新技术的油气藏测井综合评价[J].石油勘探与开发,2003,30(2):58-60.

Kuang Lichun,Mao Zhiqiang,Sun Zhongchun,et al.Reservoir synthetic evaluation based on new loging technology[J].Petroleum Exploration and Development,2003,30(2):58-60.

[13]Thomas Finkbeiner,Mark Zoback,Peter Flemings,et al.Stress,pore pressure,and dynamically constrained hydrocarbon columns in the South Eugene Island 330 field,Northern Gulf of Mexico[J].AAPG Bulletin,85(6):1007-1031.

[14]Walter H.Fertl.Abnormal formation pressures-Implications to exploration,drilling,and production of oil and gas resources[M].Amsterdam:Elsevier Scientific Publishing Company,1976:1-349.

[15]课程教材研究所.数学(八年级下册)[M].人民教育出版社，2008:38-62.

Course materials research institute.Mathematics(grade eight)[M].Beijing:The People's Education Press,2008:38-62.

[16]邓运华,王应斌.黄河口凹陷浅层油气成藏模式的新认识及勘探效果-来自BZ28-2S油田勘探历程的启示[J].中国石油勘探,2012,17(1):25-29.

Deng Yunhua,Wang Yingbin.New recognition of shallow oil and gas reservoir forming mode and exploration achievements in Huanghekou Sag-Enlightenment from exploration process of BZ28-2S oilfield[J].China Petroleum Exploration,2012,17(1):25-29.

[17]祝春荣,韦阿娟,沈东义.辽东湾地区锦州25-1油田油气成藏特点和运聚模拟研究[J].海洋石油,2011,31(3):17-22.

Zhu Chunrong,Wei A’juan,Shen Dongyi.Pooling characteristics and hydrocarbon migration and accumulation modeling research in JZ25-1 oilfield in Liaodongwan area[J].Offshore Oil,2011,31(3):17-22.

[18]周心怀,余一欣,魏刚,等.渤海辽东湾海域JZ25-1S转换带与油气成藏的关系[J].石油学报,2008,29(6):837-840.

Zhou Xinhuai,Yu Yixin,Wei Gang,et al.Relationship between JZ25-1S transfer zone and hydrocarbon accumulation in Liaodongwan offshore of Bohai Bay Basin[J].Acta Petrolei Sinica,2008,29(6):837-840.

[19]彭文绪,孙和风,张如才,等.渤海海域黄河口凹陷近源晚期优势成藏模式[J].石油与天然气地质,2009,30(4):510-518.

Peng Wenxu,Sun Hefeng,Zhang Rucai,et al.Late-stage near-source preponderant hydrocarbon pooling pattern in the Huanghekou Sag of the Bohai Sea waters[J].Oil & Gas Geology,2009,30(4):510-518.

(编辑张玉银)

A study on sand bodies connectivity in normal pressure reservoirs of the Bohai Sea with hydrostatic pressure data

Qian Geng,Zhang Jianmin,Liu Chuanqi,Zhan Lan,Yang Haifeng,Mu Pengfei,Li Xingli

(CNOOCTianjinCompany,Tianjin300450,China)

Based on the consistency of pressure system within the same reservoir,the theoretical linear relationship between formation pressure and depth is currently used as an important criterion to determine the connectivity of sand bodies within the same sequence stratigraphic framework under normal pressure.However,the linear rule for determining sandbodies connectivity has its limitations due to the influences of high permeability and fluid heterogeneity of reservoir.A new method for connectivity analysis of sand bodies is proposed based on mathematical induction,established the inverse proportional function between pressure coefficient and depth of reservoir.The properties of inverse proportional function such as intersection,monotonicity,boundedness and symmetries provide us a way to explore the relationship between inverse proportional function and reservoir pressure system,and to further determine the connectivity of two or more sand bodies.With hydrostatic pressure data from more than 50 normal pressure reservoirs out of 7 oilfields in Bohai Sea whose connectivity have been confirmed by wells,we verified the relationship between the connectivity of sand bodies and the properties of inverse proportional function of pressure coefficient and depth.The following conclusions were made.① The function image being continuous and overlapping,monotonicity and asymptote being consistent,and symmetry axis being unique are the critical criteria for determining the connectivity of sand bodies within the same sequence stratigraphic framework;② The pressure coefficient is more sensitive and reliable than the linear function;③ The curvature of inverse proportional function is affected by reservoir permeability and fluid properties,thus overcomes the limitations of linear rule.

pressure coefficient,inverse proportional function,fluid heterogeneity,permeability,normal pressure reservoir,Bohai Sea

2015-10-21;

2016-03-23。

钱赓(1986—)，男，硕士、工程师，油气田勘探与开发地质。E-mail:qiangeng@outlook.com。

国家科技重大专项(2011ZX05023-006-002)。

0253-9985(2016)04-0584-07

10.11743/ogg20160416

TE122.2

A