高阶统计约束稀疏盲反褶积技术研究与应用

张　华，庞燕青，贺振华，杨　波，何光明，巫芙蓉，陈爱萍 ，谢小翠

(1.成都理工大学 油气藏地质及开发工程国家重点实验室，四川 成都 610059；　2.中国石油 川庆钻探工程有限公司地球物理勘探公司，四川 成都 610213；　3.中国石油 物探技术试验基地 山地地震技术试验基地，四川 成都 610213；4.中国石油 新疆油田分公司，新疆 克拉玛依 834000；　5. 中国石油 新疆油田分公司 陆梁油田作业区，新疆 克拉玛依，834000)



高阶统计约束稀疏盲反褶积技术研究与应用

张华1,2，3，庞燕青4，贺振华1，杨波5，何光明2,3，巫芙蓉2，3，陈爱萍2,3，谢小翠2,3

(1.成都理工大学 油气藏地质及开发工程国家重点实验室，四川 成都 610059；2.中国石油 川庆钻探工程有限公司地球物理勘探公司，四川 成都 610213；3.中国石油 物探技术试验基地 山地地震技术试验基地，四川 成都 610213；4.中国石油 新疆油田分公司，新疆 克拉玛依 834000；5. 中国石油 新疆油田分公司 陆梁油田作业区，新疆 克拉玛依，834000)

以贝叶斯基本理论为基础，利用高阶双谱域估算的高精度地震子波为约束，在修正柯西判别准则下，实现地震数据的稀疏盲反褶积拓频处理，获取比常规反褶积提频方法分辨率更高的可靠数据。模拟数值实验和多波实际数据处理结果表明：双谱域估算的子波精度较高，以该子波为先验约束的稀疏盲反褶积能极大提高纵波和转换波数据的分辨率，满足精细解释能分辨更小薄层的要求，可作为多波高分辨率处理的有效手段。

子波估计；提频；反褶积；反射系数；地震勘探

反褶积是实际地震资料进行提高分辨率处理的主要手段。随着精细石油勘探的不断深入，对高分辨率地震资料处理的要求也越来越高，而以高斯白噪和子波最小相位为假设的传统反褶积方法无法满足地震资料分辨更小薄层的需要。

自Wiggins (1978)[1]提出了稀疏度准则——最小熵反褶积以来，随后出现了大量关于反演子波和反射系数的一大类盲反褶积技术。Canadas (2002)[2]在盲反褶积框架下，实现了地震反射系数与地震子波同时反演算法；刘财(2008)[3]等人利用自然梯度盲反褶积法估算地震子波,得到更接近于实际情况的混合相位子波,用于反褶积后的地震资料分辨率得到了提高；孟大江(2009)[4]对稀疏反褶积和高精度地震子波提取进行了深入研究；李力民等(2011)[5]采用预条件共轭梯度迭代反演地震子波和反射系数的方法。尽管这些方法反演准则、求解算法存在差异，但理论架构基本相似，都不需要白噪反射系数和最小相位假设，以通过对地震记录的子波反演后，再反演出稀疏反射系数，达到盲反褶积提频的目的，但是反射系数的求取很大程度依赖子波的精度和效率，如何高效、准确地估算出地震子波从而提高盲反褶积过程中反射系数估算精度和可信度，是在实际资料应用一个难题。

以高阶累积量和高阶谱为基础的理论从20世纪80年代发展以来，无论是从频率域还是从时间域，基于高阶累计量理论的子波估计为我们提供了新的思路，利用高阶累计量能同时估算子波的振幅信息和相位信息，通过近几年大量的学者研究，能从多解的相位中估算出精度较高的地震子波[6-7]。

本文在前人研究的基础上，提出一种高阶统计约束稀疏盲反褶积技术，把在高阶双谱域中进行多相位叠加估算出的高精度地震子波，作为贝叶斯稀疏盲反褶积的高阶约束，进行地震反射系数的高精度估算，从而在多波高分辨率处理资料中达到能分辨薄层的目的，为后续多波联合解释与反演[8-10]提供高质量的资料。

1　双谱域多相位叠加估计子波

利用地震资料的双谱进行地震子波估计，是地震资料处理中行之有效的方法。用褶积模型表示地震记录可为：

(1)

式中：s(t)，w(t)，r(t)和n(t)分别为地震记录数据、地震子波数据、反射系数数据和噪声数据；t为时间，s；*为褶积算子。

根据高阶累积量的定义和傅里叶变换公式得到双谱域地震子波估计表达式：

(2)

式中，Bs(ω1,ω2)为地震记录s(t)的双谱域数据；W(ω)为地震子波w(t)的傅里叶谱域数据；H为共轭算子；ω表示角频率，rad/s；γ3r是反射系数的三阶累计量,常数。

根据公式(2)可得到子波相位谱估计表达式：

(3)

式中：ψ(ω1,ω2)为子波双谱域相位谱数据；φ(ω)为子波的傅里叶域相位谱数据。

子波相位估算方法很多，如Brillinger[11]提出的相位重构法以及Rosenblatt[12]等提出的BMU递归算法等，但该递归算法忽略了双谱相位的平均，对初值依赖较大，不利于噪声的压制。

为了更好的解决双谱域中多值多解和抗噪性问题，提高相位估算精度，必须充分考虑双谱的平均特性，这里采用双谱域多相位叠加估算子波相位的办法。

以双谱域中两个角频率ω1和ω2的相位值为纵横坐标建立坐标系。为了便于统一计算，可把ψ(ω1,ω2)写成φ(ω1,ω2)形式，在第一象限取值，且奇偶分开，则公式(3)可表示为：

(4)

式中：M[]表示相位主值算子，将[]中的值限定在模为π的(-π,π]之内。

以此类推，横坐标相位上每个相位的相位值可通过公式(6)得到：

(6)

由上式估算出的相位没有受到模2π的影响，考虑双谱平均性，将他们叠加求平均不会引起相位多解性问题，得到最终的地震子波相位。

2　高阶统计约束的稀疏盲反褶积

基于贝叶斯理论的稀疏盲反褶积提频技术，由于其采用反演的手段重构高分辨率地震剖面，不受传统反褶积提频频带的限制的要求，可以最大程度的提高资料分辨率，满足多波等资料分辨更小薄层的要求。但该方法在求解目标函数时，需要通过多次循环迭代同时求取未知的地震子波和反射系数，在实际生产中效率过低，精度也不高，如果在双谱域中先求出高精度的地震子波，再反演目标函数求取反射系数，势必提高其处理效率的同时，得到的精度更高的反射系数。

根据褶积模型和贝叶斯理论公式可得近似式[13]：

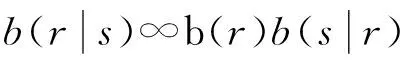
(7)

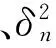
(8)

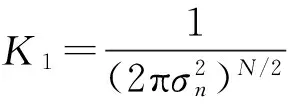
(9)

对上式(9)取对数得式(10)：

(10)

(11)

为了能在提高分辨率的同时，有效保护数据的弱反射信号，需要对目标函数进行修正的柯西准则判断，即：

(12)

把双谱域估计的地震子波矩阵W=[w0,…,wp]T带入目标函数(11)中[14]，那么对其求取反射系数r的偏导数：

(13)

图1　理论模型数值试验Fig.1　Numerical test of theoretical modela.理论实验子波;b.理论实验反射系数;c.褶积加噪合成记录;d.估算子波(红色)与理论子波(蓝色)对比; e.脉冲反褶积反射系数,红色箭头为反射系数位置;f.本文方法反射系数，红色箭头为反射系数位置

图3　 转换波数据处理前、后效果图对比Fig.3　Comparison of PS-wave data before and after processinga. 处理前转换波剖面(左)和振幅谱(右);b. 常规谱白化提频后(左)和本文方法提频后(右)转换波剖面; c. 常规谱白化提频后振幅谱(左)和本文方法提频后(右)振幅谱;d. 处理前(左)、常规方法(中)和本文方法(右)转换波储层段最大波峰振幅

(14)

(15)

3　数值实验及实际资料应用

3.1理论模型数值试验

图1c为图1a理论子波与图1b理论反射系数褶积并加噪声的合成记录，图1d为从图1c估算的地震子波与图1a理论子波的对比图。从图中可知：双谱域估算的子波与理论子波相似度高，尤其是子波的主峰和旁瓣与理论子波吻合度较高。图1f为利用本文方法得到图1c的反射系数，该反射系数与图1b的理论反射系数相似度较高，且与图1e脉冲反褶积得到的反射系数相比更加可靠、准确，证明了该方法的正确性。

3.2实际资料应用

为验证上述理论和方法的实际应用效果，选取四川盆地某地区多波资料目的层进行应用测试。

图2为纵波数据处理前后效果图对比。图2a与图2b，2c比较可知：常规谱白化和本文方法都大幅提高了剖面的分辨率，构造细节凸显，而且频谱也比处理前所有展宽。进一步比较图2b和图2c可知：本文方法对提高剖面深层同相轴的分辨率效果更好，与测井合成记录的吻合度更高，而且有效拓展高频振幅谱的同时保留了低频段信息。

图3为转换波数据处理前后效果图对比。2b与图2b，2c比较知：处理前转换波分辨率较低，采用常规谱白化处理后同相轴连续性变差，断层发育被掩盖，而利用本文方法不但大幅提高分辨率，而且同相轴连续性较好，断层清晰可见，与测井合成记录吻合度高，同时本文方法处理后的振幅谱比常规方法保留了更加丰富的低频信息和高频拓展信息。

多波多分量勘探与单一纵波勘探相比，它所能提供的地震属性信息将会成倍的增加，并能衍生出各种组合参数。利用这些参数估算地层岩性与流体等，将比仅依靠纵波的可靠性更高，可以最大限度消除利用单纯纵波进行储层预测的不唯一性。

在对纵波和转换波分量资料分别进行多种属性实验中，相对而言，振幅类属性较为稳健，因而计算了纵波和转换波最大波峰振幅类属性。从图2中纵波剖面与图3中转换波剖面中储层段T3x2—T3x1中进行最大波峰振幅分布图分析知：本文方法处理后最大波峰振幅能量更聚焦、收敛性更好，而且可见气井位于纵波中强振幅能量区(黑圈处)，并同时位于转换波弱振幅区(黑圈处)，这与储层相面含气预测结果吻合：纵波波为中强反射，转换波为弱反射，纵波强于转换波反射。

4　结论

1) 本文提出一种高阶统计约束稀疏盲反褶积技术，在高阶累计量域中利用多相位叠加，提取的混合相位子波精度高，通过子波约束稀疏盲反褶积求取的反射系数精度高、强弱能量分明。

2) 利用本文方法在实际多波资料处理中，提高分辨率明显，尤其是低分辨的转换波层序内幕更加明显，断层清晰，与测井有较好的吻合度，同相轴强弱能量更加分明，为后续研究地层岩石解释提供更好的地震资料。

[1]Wiggings R A.Minimum entropy deconvolution[J].Geoexploration,1978,16(1):21-35.

[2]Canadas G.A mathematical framework for blind deconvolution inversion problems[J].The 72nd SEG Annual Meeting,2002,2202-2205.

[3]刘财,谢金娥,郭全仕,等.一种基于自然梯度的地震盲反褶积方法[J].石油物探，2008，47(5):439-443.

Liu Cai,Xie Jin'e ,Guo Quanshi,et al.Seismic blind deconvolution based on natural gradient[J].Geophysical Prospecting Petroleum,2008，47(5):439-443.

[4]孟大江.稀疏变换反褶积和高精度子波提取方法研究[D].吉林大学，2009.

Meng Dajiang.Deconvolution based on sparse transform and high precision wavelet extraction methods[D].Jilin University,2009.

[5]李力民,姚泳汐.基于Cauchy 稀疏约束的同时迭代反演反射系数与地震子波的研究[J].重庆科技学院学报(自然科学版),2011，1673-1980.

LI Limin,YAO Yongxi.Iteration Inversion of Reflectivity Coefficient and Seimic Wavelet Based on the Cauchy Sparse Constraint[J].Journal of Chongqing University of Science and Technology(Natural Sciences Edition),2011，1673-1980.

[6]李大卫,田继东,成竹,等.基于高阶统计的混合相位子波估计及其处理[J].勘探地球物理进展，2005，1671-8585.

Li Dawei,Tian Jidong,Cheng Zhu,et al.Estimation of mixed-phase wavetet base on higher-order statistics[J].Progress in Exploration Geophysics ,2005，1671-8585.

[7]陈建,戴永寿,张亚南,等.基于高阶统计量的地震子波提取方法评价[J].石油地球物理勘探，2013,48(3):497-503.

Chen Jian,Dai Yongshou,Zhang Yanan.Evaluation approaches for wavelet pickup based on high-order statistics[J].Oil Geophysical Prospecting,2013,48(3):497-503.

[8]杨克明,张虹.地震三维三分量技术在致密砂岩裂缝预测中的应用-以川西新场气田为例[J].石油与天然气地质,2008,29(5):683-689.

Yang Keming,Zhang Hong.Application of 3D-3C seismic technique to the prediction of fractures in tight sandstone-an example from Xinchang gas field in the Western Sichuan Depression[J].Oil & Gas Geology,2008,29(5):683-689.

[9]叶泰然,付顺,吕其彪,等.多波地震联合反演预测相对优质储层——以川西深层致密碎屑砂岩为例[J].石油与天然气地质,2009,30(3):357-362,369.

Ye Tairan,Fu Shun,Lü Qibiao,et al.Application of multiwave joint inversion to the prediction of relatively high-quality reservoirs—an example from the prediction of deep tight clastic sandstone reservoirs in the western Sichuan Basin[J].Oil & Gas Geology,2009,30(3):357-362,369.

[10]袁书坤,陈开远,Bob A Hardage,等.纵波-转换横波联合反演技术在页岩气藏勘探中的应用[J].石油与天然气地质,2015,36(1):168-174.

Yuan Shukun,Chen Kaiyuan,Bob A Hardage,et al.Application of joint PP and PS inversion to the exploration of shale-gas reservoirs[J].Oil & Gas Geology,2015,36(1):168-174.

[11]Brillinger D.R.An introduction topolyspectra[J].Ann Math Statist,1965,36(1):1351-1374.

[12]Rosenblatt M,Van Ness J W.Estimation of the bispectrum[J].Ann.Math.Statist,1965,36 (1):1120-1136.

[13]李国福.盲源反褶积方法与应用研究[J].石油化工应用，2010,1673-5285.

LI Guofu.The method and applied research of blind deconvolution[J].Petrochemical Industry Application,2010,1673-5285.

[14]孙建业,高伟,刘怀山,等.基于高阶统计约束实现同态盲反褶积[J].石油地球物理勘探,2013,48(1):31-36.

Sun Jianye,Gao Wei,Liu Huaishan,et al.Seismic homomorphic blind deconcolution based on high order statistics constraint[J].Oil Geophysical Prospecting,2013,48(1):31-36.

(编辑张玉银)

Study and application of high-order statistics constrained sparse blind deconvolution technique

Zhang Hua1，2，3,Pang Yanqing4，He Zhenhua1,Yang Bo5,He Guangming2，3,Wu Furong2,3,Chen Aiping2，3,Xie Xiaocui2,3

(1.StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,ChengduUniversityofTechnology,Chengdu,Sichuan610059，China；2.GeophysicalExplorationCompany,ChuanqingDrillingEngineeringCo.Ltd.,CNPC,Chengdu，Sichuan610213，China；3.MountainGeophysicalTechnologyTestCenter,CNPC,Chengdu,Sichuan610213，China；4.XinjiangOilfieldCompany,CNPC,Karamay,Xinjiang834000，China;5.LuliangFieldOperationDistrict,XinjiangOilfieledCompany,Karamay,Xinjiang834000，China)

Based on the basic theory of Bayesian and using the high precision wavelet estimated in high-order double spectrum domain as constraints,this paper realized sparse blind deconvolution frequency-expanding processing under the modified Cauchy criteria and obtained data that are more reliable and have higher frequency than the conventional deconvolution frequency-enhancing method.The results of numerical experiments and real data processing show that the wavelet estimated in the dual spectrum domain has higher accuracy,under the priori constraint of which the sparse blind deconvolution can greatly enhance the resolution of both P-wave and PS-wave.It can meet the requirement of resolute very thin layers,thus can be used as an effective method for high resolution processing.

wavelet estimation,frequency improving,deconvolution,reflectance,seismic exploration

2015-03-02;

2016-07-10。

张华(1981—)，男，博士研究生、工程师，地球物理资料处理和反演解释。E-mail:zhanghua_sc@cnpc.com.cn。

中国石油天然气集团公司科学研究与技术开发项目(2013E-38-08)。

0253-9985(2016)04-0591-07

10.11743/ogg20160417

P631

A