考虑处理机释放时间的可分任务调度优化模型

王晓丽，王宇平，孟 坤

（西安电子科技大学计算机学院，陕西西安 710071）

考虑处理机释放时间的可分任务调度优化模型

王晓丽，王宇平，孟 坤

（西安电子科技大学计算机学院，陕西西安 710071）

可分任务调度是近年来信息技术领域研究的热点课题.已有的可分任务调度模型大多假设所有处理机在任务分配之初全部处于空闲状态，而实际上，当新的任务到来时很多处理机可能尚处于忙碌状态.每台处理机从忙碌状态转到空闲状态的时间不同，即处理机可能具有不同的释放时间.在充分考虑处理机释放时间不同的基础上，建立了一种新的混合时序约束的可分任务调度模型，并设计了高效的全局优化遗传算法求解该模型.实验结果表明了模型的合理性和算法的有效性.

可分任务调度；释放时间；混合时序约束；遗传算法

在并行与分布式系统中，大规模计算任务的处理逐渐成为了极具挑战性的课题.为系统建立合理且贴近实际的任务调度模型成了该领域最大的难点，其中可分任务调度模型［1-3］就是典型的代表之一.可分任务是指任务可以被切分为任意大小的若干子任务且子任务间不具有优先关系.在并行与分布式系统下，可分任务调度的主要目标是寻求合理的任务调度策略，使得任务的完成时间最短.

针对现实生活中常见的线性网路、总线型网络和树形网络，已经有很多文献研究可分任务调度方案的最优解.例如，文献［4］给出了齐次线性网络中任务完成时间的紧式耦合解，文献［5-6］给出了齐次树形网络与总线型网络下任务完成时间的渐进解.文献［7］给出了异构星形网络下任务最短完成时间的紧式耦合解，且证明了在遵循通信速率递减作为处理机调度顺序的情况下任务的完成时间最短.对于异构树形网络，文献［8］的研究表明处理机的调度顺序只依赖于节点的通信速率而非计算速率.然而，这些研究成果都没有考虑到处理机的计算启动开销和网络的通信启动开销.文献［9-11］研究了具有常启动开销的总线型网络中启动开销和处理机调度序列的变化对任务完成时间的影响，证明了当遵循计算速率递减作为处理机调度顺序时将获得任务的最短完成时间.文献［12］的研究表明，在具有任意启动开销的异构分布式环境下，若任务足够大，则遵循通信速率递减作为处理机调度顺序时任务的完成时间最短.文献［13］将可分任务调度模型扩展到多源网格环境中，文献［14-15］将其扩展到云计算平台，文献［16］将其扩展到无线传感器网络中，文献［17-19］将其扩展到实时环境中.

已有的研究大多假定处理机在任务到来时均处于空闲状态，然而在实际的并行与分布式应用场景中这个假设并非总是成立的.当新的任务到来时，处理机可能尚未完成前一个任务，从而处于忙碌状态，不能立即参与新任务的计算.笔者将新任务到来后，处理机由忙碌状态转变为空闲状态的时间间隔称为该处理机的释放时间.考虑处理机释放时间的可分任务调度的研究尚处于起步阶段，文献［20］给出了一种穷举方法用于同构总线型网络的可分任务调度问题.为了避免穷举法的巨额时间开销，笔者构建了一种新的考虑释放时间的可分任务调度智能优化模型，并提出了一种高效的遗传算法对模型进行求解.

1 考虑释放时间的可分任务调度优化模型

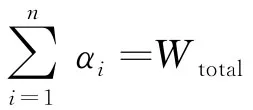
称处理机Pi（i=1，2，…，n）开始从主处理机接收任务的时刻为Pi的开始时刻，记为si.给定所有处理机的释放时间，下面分3种情况讨论处理机释放时间与开始时间之间可能满足的约束条件:

（1）ri+1≤si+zαi，i=1，2，…，n-1.处理机Pi+1的释放时间ri+1早于主处理机P0给Pi+1分配任务的时刻，即Pi+1由忙碌状态转为空闲状态发生在P0给Pi传输任务αi的过程中.

文献［3］证明了只有当所有处理机同时完成计算时任务的完成时间最短，否则完全可以将后完成计算的处理机上的部分任务调度到先完成计算的处理机上执行.由所有处理机同时完成计算，可以得到

由图1可以看出，Pi的开始时间si满足

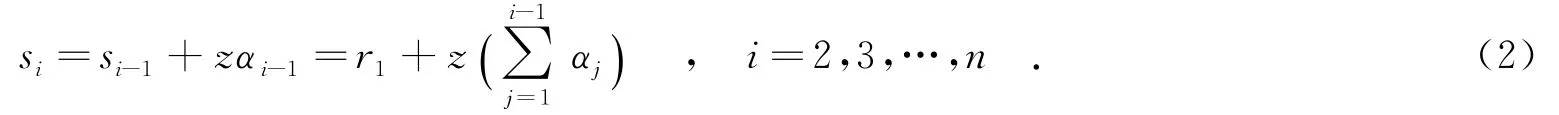
由式（1）和式（2）可得

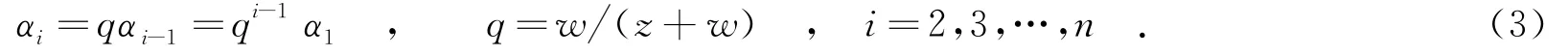
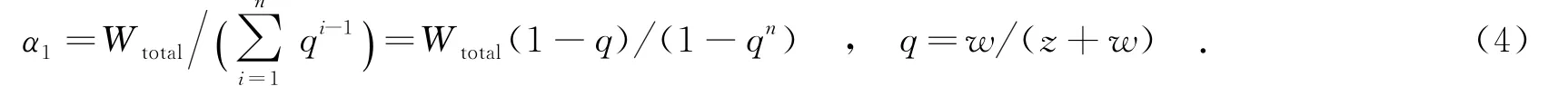
（2）ri+1＞si+zαi，i=1，2，…，n-1.处理机Pi+1的释放时间ri+1晚于P0给Pi传输完任务αi的时刻，即P0在给Pi传输完任务αi后需要等待一段时间直到Pi+1恢复空闲才能为其传输任务αi+1.同样地，由所有处理机同时完成计算可得式（1）.处理机Pi（i=1，2，…，n）的释放时间ri和开始时间si是相等的，即si=ri.将式（1）中的si替换为ri可得

（3）混合时序约束.任意两个相邻的从处理机之间可能满足约束条件（1），也可能满足约束条件（2）.若有n台处理机参与计算，所有可能的情况有2（n-1）种，图1给出了其中一种可能的情况.

将处理机Pi-1和Pi满足约束条件（1）和条件（2）的情况分别记为Γi（1）和Γi（2），其中i=2，3，…，n.用C=（c2，c3，…，cn）表示一种混合时序约束，其中ci∈｛Γi（1），Γi（2）｝.若ci= Γi（1），表明主处理机P0在给Pi-1传输完数据后紧接着为Pi传输数据，中间没有空闲.此时，处理机Pi的开始时间满足si=si-1+zαi-1.若ci= Γi（2），表明主处理机P0在给Pi-1传输完数据后需要等待Pi由忙碌转为空闲状态才能开始传输数据，中间存在空闲时间.此时，处理机Pi的开始时间满足si=ri.

以图1为例，其混合时序约束C满足C= （Γ2（1），…，Γk（1），Γk+1（2），Γk+2（2），…，Γk+m（2），Γk+m+1（1），…，Γn（1））.

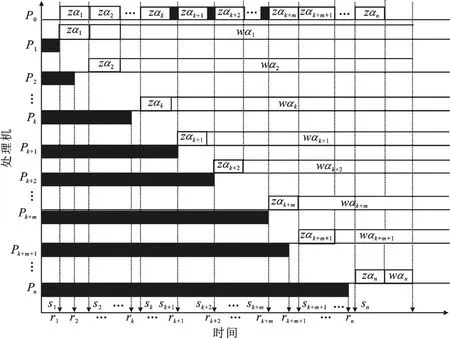
图1　一种满足混合时序约束条件的可分任务调度图

根据混合时序约束C，可以得到相邻处理机开始时间之间的关系:

将式（6）带入式（1），可得每台处理机分配的任务αi:

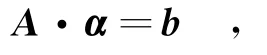
其中α表示的是待求的n×1维解变量（α1，α2，…，αn），A是n×n的系数矩阵，b是n×1维的向量.在图1给出的任务调度图中，A和b可以分别表示为

给定一种混合时序约束C=（c2，c3，…，cn），就可以求得一个形如A·α=b的标准式，进而可以采用线性规划的方法求出任务分配方案α的解.下面给出考虑释放时间的可分任务调度模型:

2 全局优化遗传算法

遗传算法已经被证明能很好地解决工程技术领域的优化、设计、控制等实际应用问题，尤其是针对任务调度等NP-hard的组合优化问题［21］.因此，笔者设计了一种新的全局优化遗传算法来求解上文提出的混合时序约束可分任务调度模型.

2.1编码与解码

笔者采用实数编码方式，将混合时序约束的可分任务调度问题表示成一个向量I=（n，H），其中n表示参与计算的处理机数目，种群初始化时设为处理机总数N；H=（h2，h3，…，hN），表示一种混合时序约束，hi∈｛1，0｝.若hi=1，表示处理机Pi-1和Pi满足约束条件（1）；反之，hi=0，表示满足约束条件（2）.

举例说明:假设共有6台处理机，一种可能的编码方案为I=（6，1，0，1，1，0），其中第1位n=6，表示参与计算的处理机数目（初始时设定为处理机总数）；h2=1，表示第1和2台处理机满足约束（1）；h3=0，表示第2 和3台处理机满足约束（2），第3和4台满足约束（1），第5和6台满足约束（1），第7和8台满足约束（2）.

2.2交叉与变异

交叉操作是遗传算法的主要进化手段，且模拟了生物繁殖和基因重组机理，通过两两染色体基因交叉互换，繁殖两个新的子代个体，并将父代好的基因遗传至子代个体.交叉操作保持了遗传算法种群个体的多样性和全局搜索能力.笔者采用两点交叉方式生成新个体:随机生成两个整数p和q，满足2≤p＜q≤N，作为交叉点，将两个父代个体交叉点之间的基因进行交换，生成两个后代个体.由于个体第1位表示参与计算的处理机数目，因此交叉后的后代个体第1位均置为处理机总数N.

变异操作是推动遗传算法进化的重要手段.通过一定概率的基因变异，保持种群多样性，强化了遗传算法的局部搜索能力.笔者采用单点变异方式生成新个体:随机生成一个整数p，满足2≤p≤N，作为变异点，将个体在该点的基因位取反，产生新的后代个体；同时，将后代个体的第1位置为处理机总数N.

2.3全局优化遗传算法

下面给出具体的遗传算法框架.

算法1 求解可分任务调度模型的全局优化遗传算法.

（1）初始化.根据编码规则随机生成初始种群P（0）.令进化代数t=0.

（2）交叉.以概率pcros从P（t）之中选择父代个体进行两点交叉.交叉获得的全部后代个体定义为集合O1.

（3）变异.以概率pmut从集合O1中选择个体进行变异.新的后代个体定义为集合O2.

（4）选择.从集合P（t）∪O1∪O2中选择最优的E个个体直接保留到下一代种群以加快收敛速度.使用轮盘赌选择操作从集合P（t）∪O1∪O2选择N-E个个体保留到下一代种群P（t+1）中.令t=t+1.

（5）终止条件.如果满足终止条件，则终止算法；否则，转向步骤（2）.

3 实验与结果分析

针对笔者提出的模型和算法，对比已有算法进行了多组实验.系统参数设置如下:处理机个数N=20，z=0.8，w=1.2，处理机P1～P20的释放时间r1～r20是指数分布的随机数.遗传算法中参数设置如下:种群大小SP=100，交叉概率pcros=0.6，变异概率pmut=0.02，精英保留个数E=5，终止条件为进化代数t=100.

表1给出了不同任务量情况下（Wtotal=1.0～10.0）两种算法对比的实验结果，其中GA代表笔者提出的全局优化遗传算法，EA代表文献［20］提出的穷举算法（Exhaustive Algorithm）.从表1可以看出，两个算法针对同样大小的任务，调度后得到的参与计算的处理机数目和任务的完成时间完全相同，可见笔者提出的算法能够有效地求出任务的最优调度策略.在算法运行时间方面，笔者提出的算法GA的运行时间远远小于穷举算法的时间，可见笔者提出的算法不仅有效而且高效.

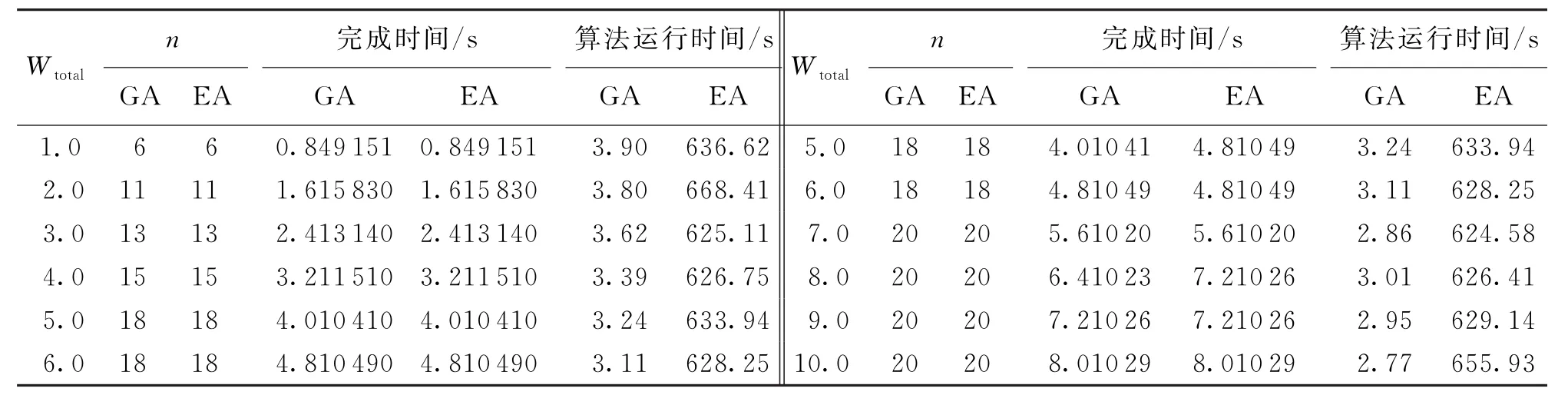
表1　不同任务量情况下全局优化遗传算法（GA）和穷举算法（EA）对比的实验结果

下面分两种情况对考虑释放时间的可分任务调度优化模型进行定性分析，着重考查任务的最短完成时间受处理机释放时间的影响.图2和图3分别表示任务较小（Wtotal=1.0～10.0）和任务较大（Wtotal=20.0 ～100.0）两种情况下，任务最短完成时间和参与计算的处理机数目随任务大小和处理机平均释放时间的变化趋势.

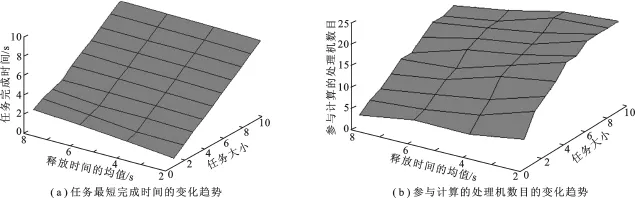
图2　在任务较小的情况下最短完成时间和参与计算的处理机数目随任务大小和处理机平均释放时间的变化趋势

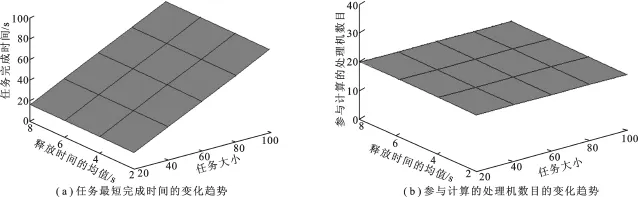
图3　在任务较大的情况下最短完成时间和参与计算的处理机数目随任务大小和处理机平均释放时间的变化趋势

由图2（a）可以看出，在任务较小的情况下，随着处理机平均释放时间和任务的逐渐增大，任务的最短完成时间也在逐渐增大.由图2（b）可以看出，对于同样大小的任务，参与计算的处理机数目随处理机平均释放时间的增大而逐渐减少.这是由于某些处理机的释放时间过大，超过了任务的最短完成时间，因而无法参与计算.随着任务的增大，任务的最短完成时间也逐渐增大，会有更多的处理机参与任务的计算.通过上面的分析可知，在任务较小的情况下，处理机的释放时间会较大程度地影响任务的最短完成时间和参与计算的处理机数目.

由图3可以看出，当任务量足够大时，所有的处理机都参与计算，任务的最短完成时间随任务量的增加近似呈线性增长趋势，处理机的释放时间对任务最短完成时间的影响几乎可以忽略.这主要是由于模型采用的是阻塞通信模式，后分配任务的处理机需要等待先分配任务的处理机完成数据的传输后才能开始接收任务，当任务量足够大时，等待时间已经超过了处理机的释放时间，所以释放时间对任务的最短完成时间不再构成影响.

4 结束语

在考虑实际并行与分布式环境下处理机存在释放时间的基础上，笔者详细分析了3种不同约束条件下的任务调度过程，进而提出了一种新的混合时序约束的可分任务调度模型，并设计了高效的全局优化遗传算法对其进行求解，实验结果表明了模型的合理性和算法的有效性.

［1］BHARADWAJ V，GHOSE D，MANI V，et al.Scheduling Divisible Loads in Parallel and Distributed Systems［M］. Los Alamitos:IEEE Computer Society Press，1996.

［2］BHARADWAJ V，GHOSE D，ROBERTAZZI T G.Divisible Load Theory:A New Paradigm for Load Scheduling in Distributed Systems［J］.Cluster Computing，2003，6（1）:7-18.

［3］ROBERTAZZI T G.Ten Reasons to Use Divisible Load Theory［J］.Computer，2003，36:63-68.

［4］MANI V，GHOSE D.Distributed Computation in Linear Networks:Closed Form Solutions［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30:471-483.

［5］BATAINEH S，ROBERTAZZI T G.Ultimate Performance Limits for Networks of Load Sharing Processors［C］// Proceedings of the Conference on Information Sciences and Systems.New York:Princeton University，1992:794-799.

［6］GHOSE D，MANI V.Distributed Computation with Communication Delays:Asymptotic Performance Analysis［J］. Journal of Parallel and Distributed Computing，1994，23:293-305.

［7］BHARADWAJ V，GHOSE D，MANI V.Optimal Sequencing and Arrangement in Distributed Single-Level Networks with Communication Delays［J］.IEEE Transactions on Parallel and Distributed Systems，1994，5:968-976.

［8］KIM H J，JEE G I，LEE J G.Optimal Load Distribution for Tree Network Processors［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32（2）:607-612.

［9］SURESH S，MANI V，OMKAR S N.The Effect of Start-up Delays in Scheduling Divisible Load on Bus Networks:an Alternate Approach［J］.Journal of Computational and Applied Mathematics，2003，46（10/11）:1545-1557.

［10］BHARADWAJ V，LI X L，CHUNG C K.On the Influence of Start-up Costs in Scheduling Divisible Load on Bus Networks［J］.IEEE Transactions on Parallel and Distributed Systems，2000，11（12）:1288-1305.

［11］SOHN J，ROBERTAZZI T G.Optimal Load Sharing for a Divisible Job on a Bus Network［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32（1）:34-40.

［12］SHANG M S.Optimal Algorithm for Scheduling Large Divisible Workload on Heterogeneous System［J］.Applied Mathematical Modeling，2008，32:1682-1695.

［13］MURUGESAN G，CHELLAPPAN C.Multi-source Task Scheduling in Grid Computing Environment Using Linear Programming［J］.International Journal of Computer Science and Engineering，2014，9（1）:80-85.

［14］IYER G N，VEERAVALLI B，KRISHNAMOORTHY S G.On Handling Large-scale Polynomial Multiplication in Compute Cloud Environments using Divisible Load Paradigm［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（1）:820-831.

［15］LIN W，LIANG C，WANG J Z，et al.Bandwidth-aware Divisible Task Scheduling for Cloud Computing［J］.Software: Practice and Experience，2014，44（2）:163-174.

［16］SHI H Y，WANG W L，KWOK N M，et al.Adaptive Indexed Divisible Load Theory for Wireless Sensor Network Workload Allocation［J］.International Journal of Distributed Sensor Networks，2013，2013:484796.

［17］MAMAT A，LU Y，DEOGUN J，et al.Efficient Real-time Divisible Load Scheduling［J］.Journal of Parallel and Distributed Computing，2012，72（12）:1603-1616.

［18］HU M，VEERAVALLI B.Dynamic Scheduling of Hybrid Real-time Tasks on Clusters［J］.IEEE Transactions on Computers，2013，99:1.

［19］HU M，VEERAVALLI B.Requirement-aware Strategies for Scheduling Real-time Divisible Loads on Clusters［J］. Journal of Parallel and Distributed Computing，2013，73（8）:1083-1091.

［20］CHOI K，ROBERTAZZI T G.An Exhaustive Approach to Release Time Aware Divisible Load Scheduling［J］. International Journal of Internet and Distributed Computing Systems，2011，1（2）:40-50.

［21］COSTA A，CAPPADONNA F A，FICHERA S.A Novel Genetic Algorithm for the Hybrid Flow Shop Scheduling with Parallel Batching and Eligibility Constraints［J］.The International Journal of Advanced Manufacturing Technology，2014，75（5-8）:833-847.

（编辑:郭 华）

Release time aware divisible-load scheduling optimization model

WANG Xiaoli，WANG Yuping，MENG Kun
（School of Computer Science and Technology，Xidian Univ.，Xi’an 710071，China）

Divisible-load scheduling has become an increasingly hot subject in the research on information technologies in recent years.Most existing divisible-load scheduling models assume that all processors are idle at the beginning of workload assignment.In fact，many processors may still in the busy state when a new workload arrives.Processors may have different waiting times from the busy state to the idle，that is，processors have different release times.This paper proposes a new release time aware divisible-load scheduling model with hybrid time constraints and designs an effective global optimization genetic algorithm to solve it.Finally，experimental results show the effectiveness of the proposed model and the efficiency of the proposed algorithm.

divisible-load scheduling；release time；hybrid time constraints；genetic algorithm

TP301

A

1001-2400（2016）01-0047-07

10.3969/j.issn.1001-2400.2016.01.009

2014-08-11 网络出版时间：2015-04-14

国家自然科学基金资助项目（61402350，61472297，61272119）；中央高校基本科研业务费专项资金资助项目（JB150307）

王晓丽（1987-），女，讲师，博士，E-mail:wangxiaoli@mail.xidian.edu.cn.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20150414.2046.006.html