基于拓扑优化的非均匀蜂窝结构设计与建模
2016-09-12文定良鑫WENDingliangJINXin神华包头煤化工有限责任公司包头0400国防科学技术大学机电工程与自动化学院长沙40073
文定良,金 鑫WEN Ding-liang, JIN Xin(.神华包头煤化工有限责任公司,包头 0400;.国防科学技术大学 机电工程与自动化学院,长沙 40073)
基于拓扑优化的非均匀蜂窝结构设计与建模
文定良1,金 鑫2
WEN Ding-liang1, JIN Xin2
(1.神华包头煤化工有限责任公司,包头 014010;2.国防科学技术大学 机电工程与自动化学院,长沙 410073)
蜂窝填充是实现结构轻量化的重要手段。针对均匀蜂窝结构未考虑最优传力结构布局的缺点,提出了一种基于拓扑优化的非均匀蜂窝结构建模方法。对受力结构进行拓扑优化,将优化密度结果映射为蜂窝胞元的相对密度分布矩阵,通过用户自定义特征以及参考基准的循环定义提高建模的自动化程度,实现非均匀蜂窝结构的快速建模。仿真结果表明,非均匀蜂窝结构力学性能更优,验证了该方法的有效性。
蜂窝结构;拓扑优化;CAD建模;ANSYS仿真
0 引言
在航空航天、轨道交通等行业产品的设计中,结构的轻量化不仅可以减少产品制造与运行的能源消耗,而且可以为产品带来更远的射程、更高的机动性以及更优越的动静态性能,是关系到产品竞争力的关键指标。近年来随着材料制备和成形加工技术的迅速发展而出现的超轻蜂窝结构是以高孔隙率为特点,包含贯通或非贯通的二维或者三维孔隙的一类新颖多功能结构[1]。蜂窝结构具有低相对密度的特点,在结构减重的同时具有高比强度和比刚度,可以实现抗冲击[2]、高效传热与隔热[3]、电磁波吸收、吸声降噪[4],满足多功能化的要求[5]。传统蜂窝结构属于周期性结构,相对密度分布均匀,制备工艺成熟,虽然从胞元尺度上来看其微结构是优化后的结构,但是从宏观尺度上来说属于未优化的均匀结构,这样均匀分布的结构没有考虑最优传力路径,轻量化效率不高。
拓扑优化是在满足性能条件下实现轻量化目标的重要手段,其本质是在一定的外力和约束作用下,寻求具有最佳传力路径的结构布局形式[6]。拓扑优化在汽车、航空航天、土木工程以及工业装备等领域的结构设计中发挥了越来越大的作用[7,8],目前商业应用最成熟的是Rozvany[9]提出的SIMP(固体各向同性材料惩罚模型)方法,以设计空间每个单元的密度作为设计变量,最优设计结果是结构各部分的0~1之间的密度分布,可以将拓扑优化的最优密度结果向蜂窝胞元的相对密度进行映射,从而得到非均匀的蜂窝结构,在宏观结构和细观胞元两个尺度实现结构的优化设计,提高结构轻量化效率。
蜂窝结构的建模有两种方式,一是使用CAD平台进行交互式建模,其问题在于:由于蜂窝胞元的非均匀特性,不便于使用阵列或镜像等具有周期性的操作进行直接建模,手动建模复现难度大,成本高,时间周期长。二是使用快速成型前处理软件,例如Magics。这一类软件为基于STL格式模型的固定单元填充,该方案进行非均匀蜂窝结构建模的主要问题在于:非均匀结构实现困难,基本都只有均匀胞元填充功能,建模对象为STL格式,不利于优化设计后的结构处理调整,若结构生成后出现细节缺陷,需要返回CAD软件中进行修改。因而,通过引入适当的方法对CAD软件进行二次开发,提高建模自动化程度对于非均匀蜂窝结构的建模具有重要意义。
1 结构拓扑优化设计
对于非均匀蜂窝结构的拓扑优化,其参照结构是均匀密度的蜂窝结构,即通过拓扑优化实现在相同的减重比情况下的最大刚度。依据文献[10]给出最小柔顺性问题的一般性定义:在给定材料体积约束条件下,寻求设计域内材料的最优分布,实现最大化刚度的结构拓扑优化设计。因此对结构建立最小柔顺度优化模型,以单元相对密度作为设计变量,在体积约束下求最大刚度,进行拓扑优化建模。
优化的目标函数为结构最大化刚度,也就是结构的柔度最小,柔度表达式为:

其中K是结构的整体刚度矩阵,可以表达为单元密度的函数,U是结构的位移矩阵,F是结构所受外力。约束条件包括体积约束、单元密度范围约束以及其他约束。体积约束表示结构在固定的体积百分比范围内进行单元密度排布,约束体积分数取初始均匀蜂窝结构的体积分数。单元密度范围约束为考虑到密度过小单元胞壁过薄以及密度过大单元中心孔过小,都不利于制造,因此最小密度和最大密度取0.2和0.9。其他约束包括在设计时需要考虑的制造、使用方面的其他要求,以表示。由此可得,进行等效连续体结构拓扑优化的数学模型为:

针对建立的优化模型,进行问题的求解的关键步骤是进行灵敏度分析,求得目标函数C对设计变量xe的灵敏度[10]:

针对壁厚梯度约束等特定的设计要求,过滤并更新灵敏度函数,基于目标函数的灵敏度,采用优化准则算法优化更新设计变量[11]。
2 胞元密度矩阵映射
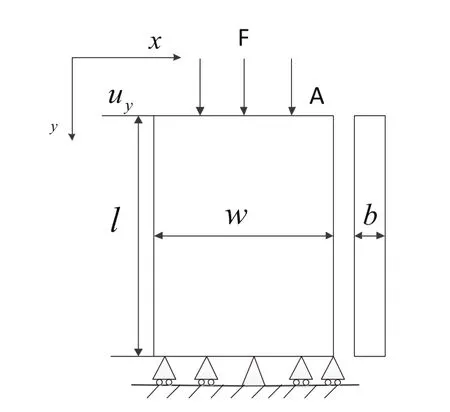
图1 设计对象的几何结构与受力状况
针对具体设计对象如图1所示,为长120lmm=,宽w=60mm,厚度b=10mm,顶端承受均布压力F=60N的固体板状设计域,胞壁实体材料弹性模量E=7.2×1010Pa,泊松比v=0.3。因为只承受蜂窝胞壁方向的力,参考Wang[12]进行的包括六边形蜂窝、正方形蜂窝、全三角蜂窝在内的典型蜂窝结构力学性能对比分析,选择正方形胞元构造变密度的蜂窝结构。以优化求解得到的单元密度矩阵为基础,将胞元所在有限单元密度进行平均运算,映射求解胞元密度分布矩阵。具体过程如图2所示,分为以下三步:
1)输入参数确定。包括设计域长度length,设计域宽度width,胞元尺度a,拓扑优化有限单元尺寸r,拓扑优化单元密度矩阵xe。
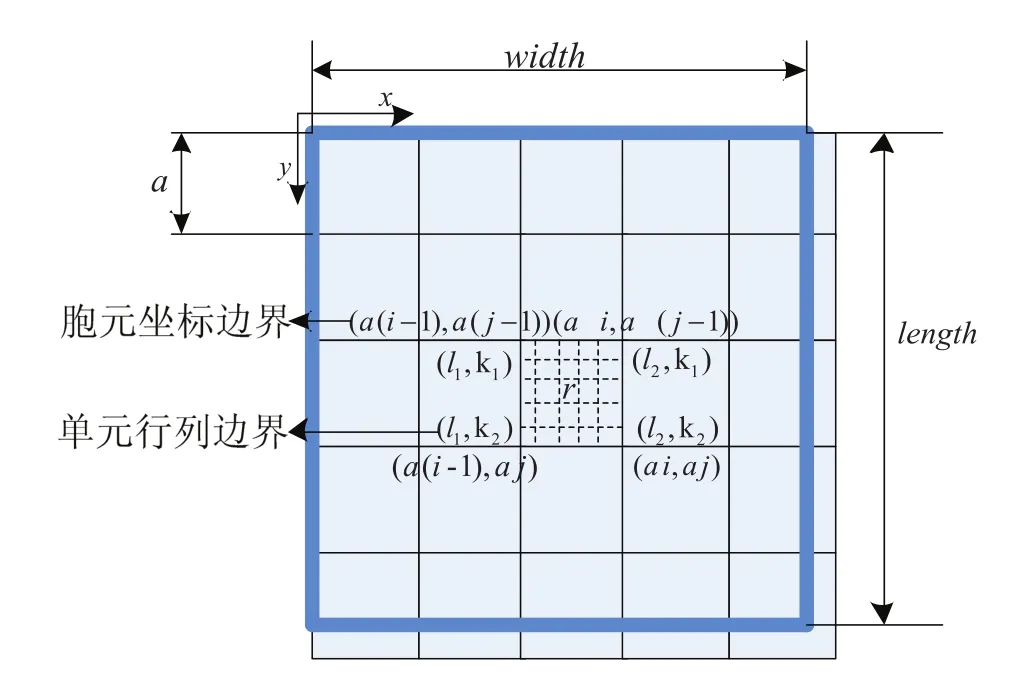
图2 密度映射示意图
2)胞元排布确定。以设计域左上角顶点作为胞元排布起始点,x方向胞元排布数目为y方向胞元排布数目为其中ceil表示可能出现边缘胞元超出设计域情况,进行向上取整。
3)胞元密度矩阵求解。针对行为j、列为i的胞元。其胞元边界坐标为:

胞元所在有限单元密度矩阵的对应边界行列为:
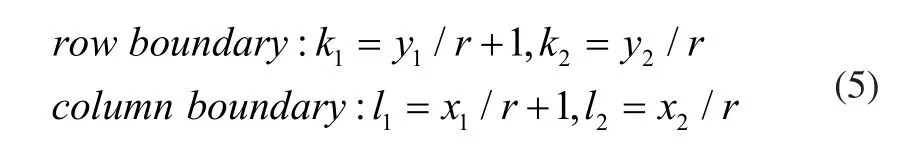
对行列范围内的有限单元密度进行平均化求解,得到胞元的映射密度:

3 非均匀蜂窝结构建模
以映射得到的胞元排布和密度矩阵为输入,进行变密度蜂窝结构的建模,本文选择PTC公司的Creo作为结构建模CAD软件,使用Creo中的用户自定义特征(UDF)方法简化建模过程,基于其功能丰富的Pro/ Toolkit函数库进行Creo的二次开发,编写变密度蜂窝结构自动建模生成的辅助应用程序。
非均匀蜂窝结构建模的总体流程如图3所示,首先分析需要导入的蜂窝胞元特征,建立参数化模型与参考基准列表,依此完成胞元UDF的创建。正方形胞元结构UDF示意图如图4所示。图中关键参数与参考基准如表1所示。构成参数化的UDF。
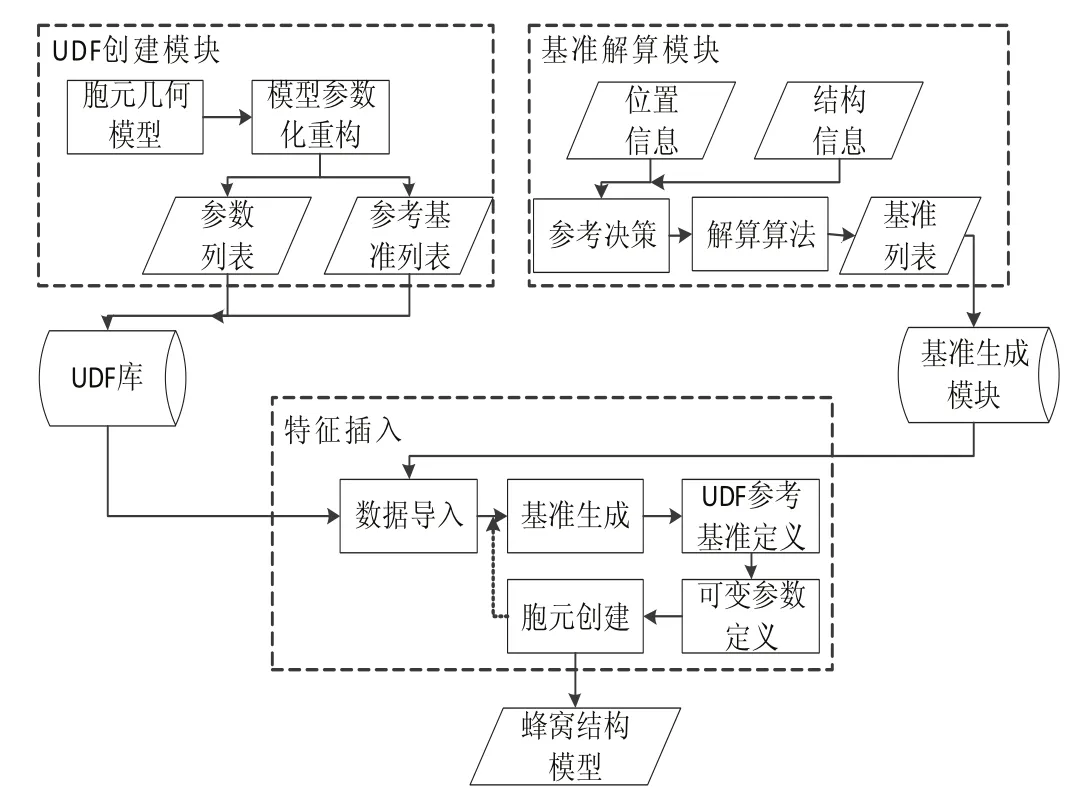
图3 非均匀蜂窝结构建模流程图

图4 正方形胞元结构UDF
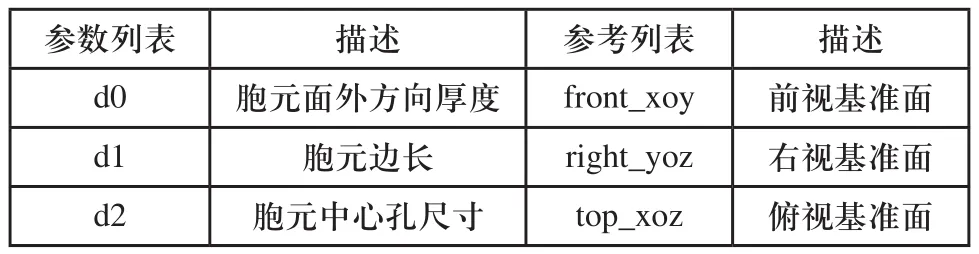
表1 正方形胞元参数与参考列表
胞元尺寸参数与胞元相对密度x之间满足以下关系式,从而确定各胞元的基本参数取值。

第二步将依据位置信息与胞元结构信息生成基准的功能封装为基准生成模块,基准面的类型包括默认基准面与偏距基准面。默认基准面是系统在默认初始坐标系下的三个标准正交平面,是起始胞元的参照;其他胞元的基准为偏距基准面,以默认基准面为参考,需要定义偏距值以及基准排布个数,其中偏距值为胞元边长d1,基准排布为第2节中确定的x方向胞元排布数目和y方向胞元排布数目。
最后将胞元UDF与基准生成模块结合,导入设计域尺寸、胞元外形尺寸以及胞元密度矩阵数据,基于这些数据进行参考基准的生成及可变参数的赋值,实现对各个单胞的空间位置及形状的循环定义,生成变密度蜂窝结构模型。
4 结果及其分析
图1所示对象的拓扑优化密度分布以及非均匀蜂窝结构建模结果如图5所示。经过密度映射以及CAD建模后的蜂窝结构模型完整无缺陷,能够较好地反映拓扑优化的密度分布。
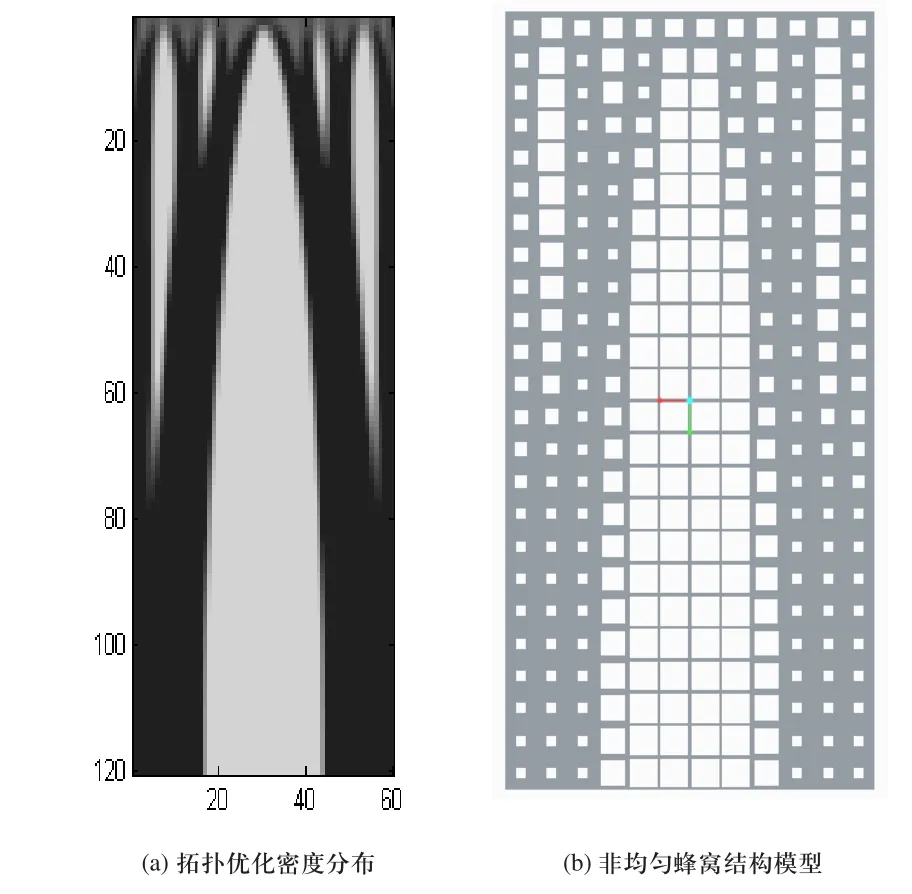
图5 优化设计与蜂窝结构建模结果对比
采用ANSYS作为仿真分析工具,对均匀蜂窝结构以及非均匀蜂窝结构的抗压刚度进行分析对比,其中uy为受压顶部所有单元的y方向平均位移,F为顶部受到的压力。蜂窝结构受压变形如图6所示。

图6 蜂窝结构受压变形对比
计算得到均匀蜂窝结构的抗压刚度为145197N/ mm,非均匀蜂窝结构的抗压刚度为164383N/mm,刚度提升幅度为13.2%,在相同减重比情况下,拓扑优化后的变密度蜂窝结构抗压刚度相比均匀密度蜂窝结构刚度有明显提高,验证了基于拓扑优化的非均匀蜂窝结构建模的有效性。
5 结论
1)提出了一种基于拓扑优化的非均匀蜂窝结构建模方法。对受力结构进行拓扑优化,将优化密度结果映射为蜂窝胞元的相对密度分布矩阵,通过用户自定义特征以及参考基准的循环定义提高建模自动化程度,实现非均匀蜂窝结构的快速建模。
2)经过密度映射以及CAD建模后的蜂窝结构模型完整无缺陷,能够较好地反映拓扑优化的密度分布。
3)分析对比了均匀蜂窝结构以及非均匀蜂窝结构的抗压刚度,结果表明优化后的非均匀蜂窝结构抗压刚度性能更优,验证了基于拓扑优化的非均匀蜂窝结构建模方法的有效性。
[1] Wadley H N G.Multifunctional periodic cellular metals[J].Phil Trans R Soc A,2006,364:31-68.
[2] Elnasri I,Pattofatto S,et al.Shock enhancement of cellular structures under impact loading: Part I Experiments[J].J Mech Phys Solids,2007,55(12):2652-2671.
[3] Tian J, Kim T,Lu T J, et al. The effects of topology upon fluidflow and heat-transfer within cellular copper structures[J].Int J Heat Mass Transf,2004,47:3171-3186.
[4] Wang J, Lu T J,Woodhouse J, et al. Sound transmission through lightweight double-leaf partitions: theoretical modeling[J].J Sound Vibr,2005,286:817-847.
[5] Fan H L, Jin F N, Fang D N.Mechanical properties of hierarchical cellular materials: Part I Analysis[J].Compos Sci Technol, 2008,68:3380-3387.
[6] 左孔天.连续体结构拓扑优化理论与应用研究[D].长沙:国防科学技术大学,2010.
[7] Zuo Kongtian. Research of theory and application about topology optimization of continuum structure[D].Changsha:National University of Defense Technology,2010.(in Chinese)
[8] Gil Ho Yoon.Maximizing the fundamental eigenfrequency of geometrically nonlinear structures by topology optimization based on element connectivity parameterization[J].Computers and Structures,2010,88:120-133.
[9] Soren Halkjær, Ole Sigmund,Jakob S Jensen.Maximizing band gaps in plate structures[J].Struct Multidisc Optim,2006,32:263-275.
[10] Rozvany GIN, Zhou M,Birker T. Generalized shape optimization without homogenization[J].Struct Optim,1992,4:250-254.
[11] Bendsoe M P. Topology Optimization:Theory,Methods and Applications[M].Berlin: Springer,2003.
[12] Erik Andreassen,Anders Clausen,et al.Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip.Optim,2011,43(1):1-16.
[13] Wang A J, McDowell D L. In-plane stiffness and yield strength of periodic metal honeycombs[J].ASME J Eng Mater Technol,2004,126:137-156.
Design and modeling of non-uniform honeycomb structures based on topology optimization
TN95
A
1009-0134(2016)08-0130-04
2016-07-29
文定良(1964 -),男,湖南人,高级工程师,工程硕士,主要工作内容为石油化工及煤化工的设备技术管理及工程管理。
