半潜式钻井平台姿态运动监测系统研究

徐 涛，刘清友，黎 伟

（1.西南石油大学 机电工程学院，成都 610500；2.西南石油大学 油气藏地质及开发工程国家重点实验室，成都 610500）

半潜式钻井平台姿态运动监测系统研究

徐 涛1，刘清友2，黎 伟1

（1.西南石油大学 机电工程学院，成都 610500；2.西南石油大学 油气藏地质及开发工程国家重点实验室，成都 610500）

针对深海石油钻井开发过程中半潜式钻井平台的姿态测量问题，提出一套基于姿态监测技术、使用相关姿态传感器来进行实时姿态测量的半潜式钻井平台监测系统架构。就加速度计传感器、陀螺仪传感器和方位角度传感器这3类辅助运动传感器，在姿态信息测量过程中的信号干扰和表达方式差异带来的测量精度不高等问题，采用 UKF滤波算法和四元数收敛算法加以解决。依据平台姿态监测系统所测量数据和解算结果，对半潜式钻井平台的基本运动参量进行求解，得到半潜式钻井平台在纵荡、横荡和升沉运动过程中三轴向线性加速度分量的数学表达式。该姿态监测系统可为平台复杂运动机理研究和相关升沉补偿装置设计提供理论和数据支持，使该系统在实际工况条件下具有应用前景。

半潜式钻井平台；姿态监测；UKF滤波；四元数；海洋钻井

0　引 言

近些年来，油气开采方向开始逐渐由陆地转向拥有丰富资源储量的海洋。作为核心装备的浮式钻井平台，在风浪等环境载荷作用下会产生纵荡、横荡和升沉的直线运动以及首摇、横摇和纵摇的旋转运动等，构成6个自由度的复杂姿态变化运动，其中升沉运动对钻井作业影响最大。目前，半潜式钻井平台（船）或海洋船舶中使用的动力定位系统，有关平台或船舶的位置测量系统是该动力定位系统实现高精度定位的核心部分。随着20世纪60年代第一代动力定位装置［1，2］的运用，到20世纪70年代运用现代控制理论（包括卡尔曼滤波技术和线性二次型高斯随机最优控制理论等）［3］提高定位精度的第二代动力定位系统的出现，动力定位系统中有关位置测量技术的发展迅速，基本能保证对平台状态的较好估计和控制器的平滑输出。20世纪90年代，随着计算机技术的发展，基于智能控制和测量技术的第三代动力定位系统［4，5］取得了较快进展。

现代动力定位系统的各推力器在位置测量系统和控制系统的操纵下，可对钻井平台（船）产生横向推力、纵向推力、回转力矩及其组合，保证钻井平台在海平面内稳定且保持在作业点处。由于动力定位系统主要用于控制钻井平台的慢漂运动等在海平面内的运动，而对平台在升沉运动平面内的上下升沉运动无法控制和补偿，需要另设的升沉补偿装置［6］对该升沉运动量进行补偿，保证钻井作业顺利进行。

利用姿态监测技术对半潜式钻井平台的运动参量测定进行相关研究，需先在三维空间里设定一个地理固定参考系 O-ENZ，再将任一变化的坐标系O-x1y1z1固定于平台上，随平台的旋转振荡而保持运动状态的一致性，坐标系的取向可用三个欧拉角α、β和γ表示（见图1）。

利用该姿态运动监测系统，实时准确掌控钻井平台在三维空间的姿态信息，特别是升沉运动平面内的平台运动参量，并在此基础上利用升沉补偿装置对钻井平台的升沉运动进行及时补偿，该举措是钻井作业高效进行的技术保障，也是该监测系统的主要设计用途。

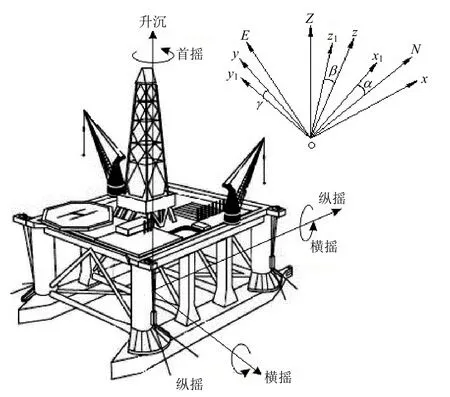
图1　半潜式钻井平台姿态运动

1　系统架构设计

浮式钻井平台的姿态测量是对其进行相关运动控制和补偿的基础，该测量过程是运用不同类型的姿态传感器或其组合对所测信息进行实时解算的过程，近些年国内外对浮式钻井平台在环境载荷作用下位置监测技术研究［7，8］有较大进展。姿态传感装置是基于微电子机械系统技术的高性能三维运动姿态测量系统［9，10］，在航天航海测控和智能机器人控制等领域应用广泛。姿态测量系统需要在变化的坐标系三轴向上分别设置有加速度计、陀螺仪和方位角度传感器等辅助运动传感器，并使用滤波器过滤干扰信息和杂波，再用内置低能耗微处理器输出经过误差校准的数据，数据处理过程基于欧拉角到四元数的转换算法进行姿态测量数据转化，以实现实时输出零漂移三维姿态数据，避免运动角变化较大时采用欧拉角所附带的奇异现象，并将传感器所获得姿态数据汇总并解算出钻井平台的升沉运动状态信息，为研究钻井平台的相关升沉补偿机理和设计升沉补偿装置提供理论依据。

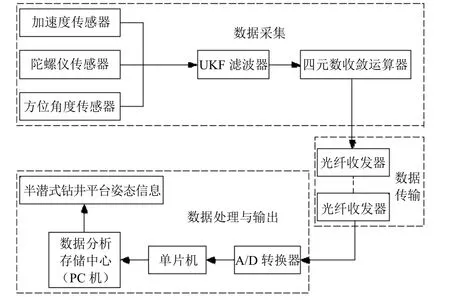
图2　半潜式钻井平台姿态监测系统架构

浮式钻井平台是深海石油开发的重要设施之一。与一般依靠固定在海底的导管架浅海平台不同，深海半潜式平台通过动力定位或锚链系泊方式［11］停留在水下井口上方的作业点处，由于此时受外界环境载荷的影响，钻井平台做升沉运动，因此，对平台姿态信息和运动规律进行相关监测具有重要意义，该姿态监测系统的具体架构形式见图2。

为满足对半潜式平台复杂姿态信息监测的需要，该系统架构由数据采集、数据传输和数据处理与输出3部分构成，姿态监测设备包括基于MEMS的加速度计传感器、陀螺仪传感器和方位角度传感器。

1.1数据采集

加速度计传感器［12，13］主要用于对半潜式钻井平台在风浪等环境载荷作用下相对于固定坐标系的纵荡、横荡和升沉运动的线性加速度值的测量；陀螺仪传感器［14］依据科里奥利加速度在驱动和检测模式两者之间进行能量交换和转移的原理制成，核心部件采用受外界驱动时在芯片平面上进行振荡的机械元件，能响应相同平面上其他振荡动作而进行的旋转动作测量物体绕中心旋转轴的角速度，在钻井平台姿态监测过程中主要用于测量横摇、纵摇和首摇三运动的角速度值；方位角度传感器用于度量平面物体之间角度差，能测量浮式平台上某点在指北方向O-N线起，依顺时针方向到目标方向线之间的水平夹角。

1.2数据传输

姿态监测系统将传感器采集的数据信息通过光纤输送到数据处理与输出部分，光纤传输具有传导性能好，传输信息容量大等特点，适合于大容量复杂姿态信息的传输。系统中需要在光纤线路两端安装光纤收发器，该收发器是一种将短距离双绞线电信号和长距离光信号进行互换的以太网传输媒体转换单元。

1.3数据处理与输出

姿态信息数据经过光纤线路传输进入A/D转换器中，将传感器采集所得的模拟电信号转化为可被计算器识别的数字信号，再通过单片机对数据进行处理和初步分析，得到半潜式钻井平台在风浪等环境载荷作用下的全姿态信息，并利用其能耗低、速度快和输出接口丰富等特点，将信息实时输入到拥有更大存储空间和运算分析能力的PC机中存储显示，以便对平台姿态信息进行全程监控和实时存储备份。

利用PC机强大的分析能力，通过对获得数据的编程分析，得到钻井平台在升沉运动过程中的运动幅值参数和变化规律，并在显示器上直观显示，然后将得到的平台升沉运动位移数据信息输入到升沉补偿装置控制器中，使升沉补偿装置及时动作以取得补偿效果。通过实测姿态数据中有关升沉补偿规律的分析研究，可为设计研发新型高效的升沉补偿装置提供数据支撑和实验验证。

1.4系统布置与安装

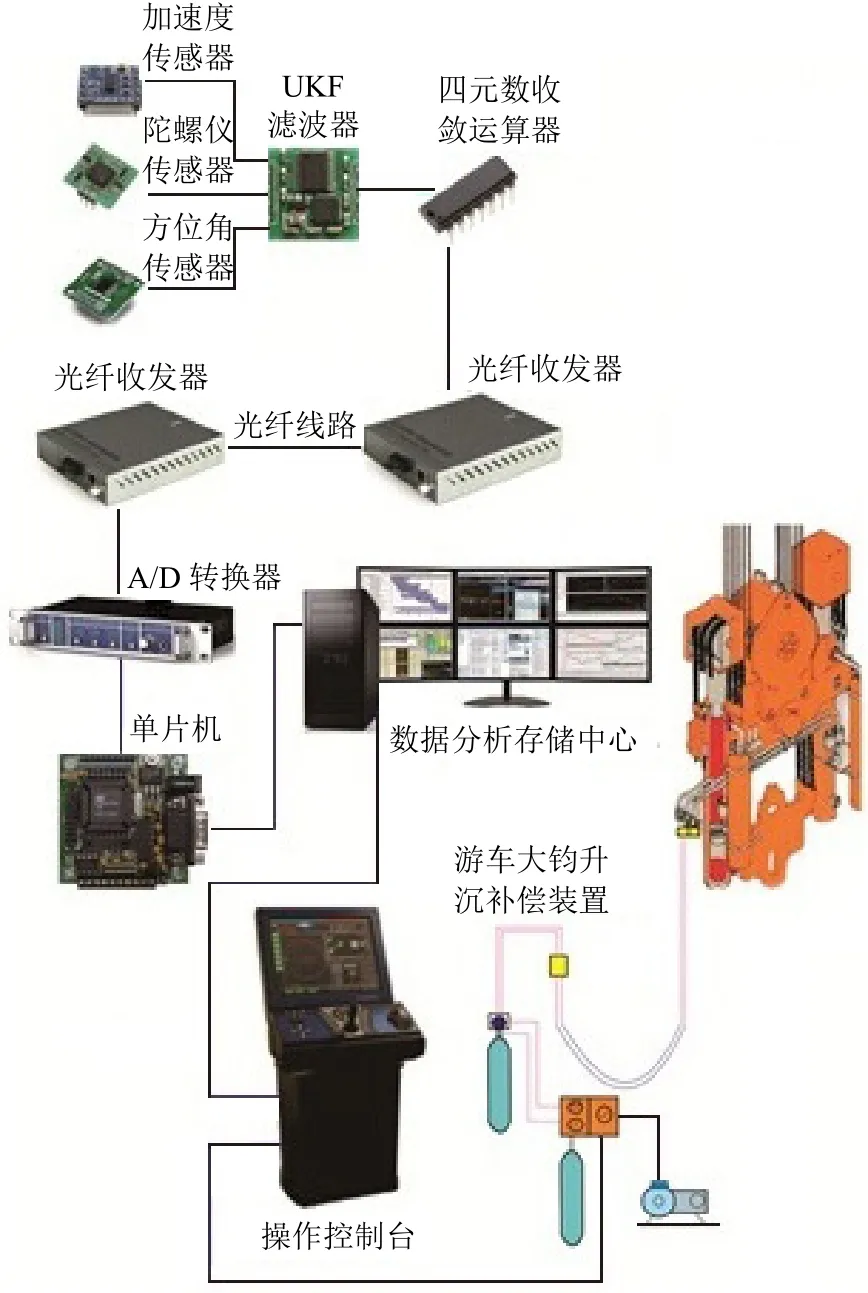
图3　平台数据采集系统布置

依据图 2所示的半潜式钻井平台姿态监测系统构架，该姿态监测系统中包含的数据采集、数据传输、处理和输出3大部分，按照不同部分所承担的任务差异在钻井平台上进行合理布置（见图3）。数据采集部分中的3类监测传感器分别按照X，Y，Z三轴向设置，经防水封装后与 UKF滤波器和四元数收敛运算器三者一起放置在预先设计的数据采集器件封装盒内，然后将该封装盒安置在半潜式钻井平台的上甲板边缘，并在每侧甲板设置3套数据采集系统；数据采集部分的数据传输到光纤收发器后，经转换使数据能在光纤中传送到半潜式钻井平台控制中心的监测系统数据处理与输出部分，并在此完成整套监测系统所测数据的分析处理工作；平台升沉运动位移信息通过电路传输给操作控制台，由其控制钻井平台升沉补偿装置的运作，对环境载荷作用时平台的升沉位移进行补偿。

2　模型解算

2.1UKF（Unscented Kalman Filter）无损滤波算法

由于半潜式钻井平台甲板空间有限，各类电子监控设备和用电设备安装密度大，使用频繁。这些设备在接入电路或启断过程中将产生的尖峰脉冲或电磁波通过电源线或电磁耦合形式等途径进入运算放大电路，对传感器工作造成各种形式的信号干扰。为保证各类传感器监测信息的准确性，需要采用滤波器对电路中夹带的干扰信息进行过滤处理。

一般在线性或非线性强度较低的系统中选用卡尔曼或扩展卡尔曼滤波器进行滤波处理。由于海洋环境复杂多变、平台所安装的电磁设备众多，对钻井平台姿态监测传感器的干扰影响因素较多，多种外界因素对平台产生的干扰形式多样且具有随机性，导致整体系统的非线性度较大。系统中的测量模型和状态模型皆为非线性，使用卡尔曼或扩展卡尔曼滤波算法会出现稳定性差和测量精度不高的缺陷，因此对钻井平台姿态监控的滤波过程中，针对实际海洋环境和众多设备复杂干扰的特性，选择UKF无损滤波方法［15］，通过样本点和加权点的使用，经过非线性状态方程获得n维样本点更新后的滤波值，克服使用扩展卡尔曼滤波算法的缺陷并实现对目标有效的跟踪。

假设半潜式钻井平台的系统动态方程为随机非线性不变的离散方程，其状态方程和测量方程［16］为：

在第i时刻，钻井平台的系统状态估计和协方差矩阵分别设为xˆ（ i| i）和P（ i| i），状态维数为nx，即可得：

由式（1）计算所选取样本点状态的一步预测为：

样本点状态的预测协方差为：

由此得到半潜式钻井平台系统的增益矩阵、状态估计矩阵及其协方差矩阵为：

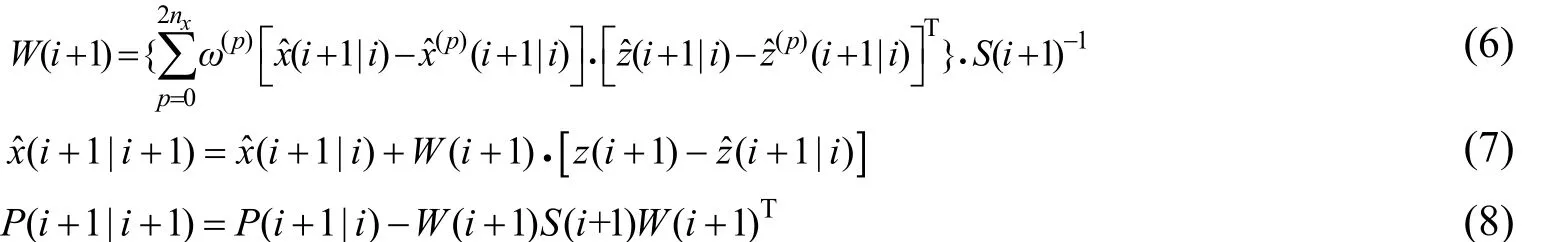
通过对半潜式钻井平台的滤波处理结果分析可得：UKF滤波算法通过对非线性函数的概率密度分布进行处理，使用确定的样本点数据来逼近系统状态的后验概率密度，不用求解雅可比行列式，未忽略高阶项，其精度比卡尔曼滤波算法高，能使计算过程简化且容易实现。

2.2四元数收敛算法

在对钻井平台三维运动分析过程中，为及时表达其在三维空间的姿态数据，常使用连接于空间物体的随动坐标系中3个正交单位矢量对地理固定坐标系的方向余弦矩阵表示，但该矩阵表达结果不直观，对及时掌握对象的方向参数带来不便。为使得钻井平台方向姿态信息的直观表达，便于对空间运动状态进行分析，使用围绕固定于刚体坐标轴的3个转动复合轴量的欧拉角进行表述。

在姿态运动学方程中，当某一坐标轴方向上的角度变化较大时，欧拉角表示过程中会出现奇异现象。为避免奇异现象对测量造成的误差，需要使用超复数形式的四元数［17，18］对欧拉角转换，同时还可以减小整体运算量，使算法得到较高的精度。

将半潜式钻井平台坐标系记为O-xyz，地理坐标系记为O-ENZ，随动坐标系记为O-x1y1z1且随平台相对于地理固定坐标系运动（见图4）。平台纵轴x在水平面上的投影与地理固定坐标系轴向O-N的夹角为α，在纵轴x水平向做摇摆运动时横轴y与横向水平轴夹角为γ，在横轴y向做摇摆运动时垂轴z与垂向水平轴夹角为β。

由欧拉角变换公式可得到钻井平台随动坐标系O-x1y1z1相对地理固定坐标系的角速度分量在O-xyz坐标系三轴向的投影数值量为：

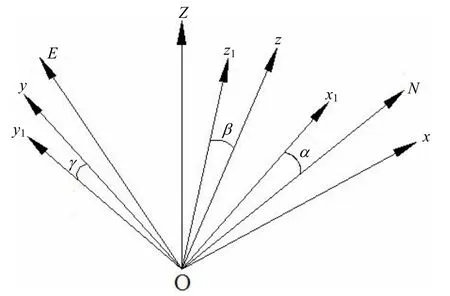
图4　浮式钻井平台坐标体系

利用刚体做转动时的相关原理［19］得出半潜式钻井平台姿态四元数的运动方程式如下：

求解该运动方程得到四元数组合形式的半潜式钻井平台的姿态矩阵ZJn，如式（11）所示：

再利用超复数映象相关概念［20，21］求得将欧拉角表达转换为四元数表示的转化公式为：

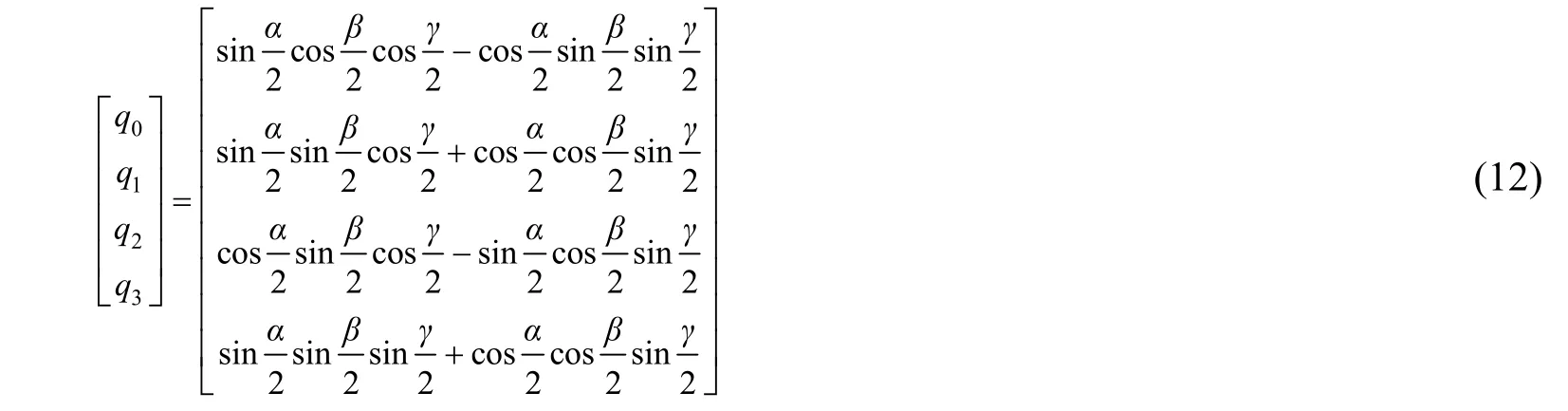
2.3半潜式钻井平台运动参量的解算

半潜式钻井平台在深海钻井过程中受到风浪、海流等环境载荷作用时［22］，平台的重心会相对于三维空间产生平移和绕坐标轴转动两类运动，所以钻井平台运动姿态的轨迹变化可看作是由随自身重心一起做平移运动和旋转运动的矢量合成。

在任一指定的三维空间坐标系中（见图4），对于物体加速度的求解［23］过程，设半潜式钻井平台上选定的固定一点S坐标定为（x，y，z）位移矢量定义为，平台重心O点的绝对线性加速度矢量为，S点的绝对线加速度矢量为，平台整体绕重心O点的旋转角速度和角加速度分别为和，各加速度矢量和角速度矢量、、和在坐标系中的坐标设为和，结合式（9）得半潜式钻井平台重心O点的加速度分布为：

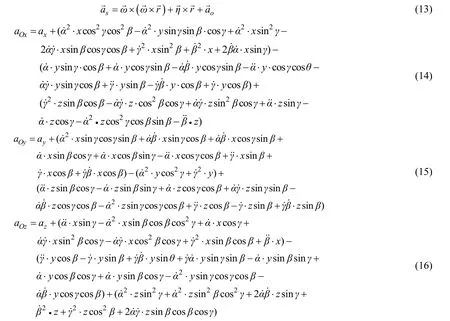
根据图1可知，设半潜式钻井平台在做纵荡、横荡和升沉运动时的线性加速度分别为Ay、Ax和Az，由式（14）、式（15）和式（16）经过线性变化后，可得安装有姿态监测系统的钻井平台线性加速度分布为：

由此可得到半潜式钻井平台在做升沉运动时的线性加速度大小如式（18）所示：

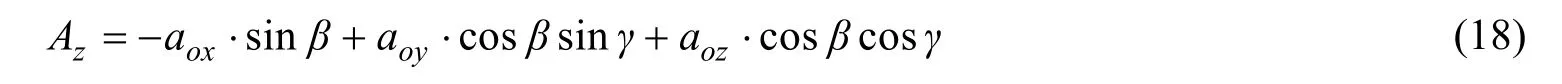
利用姿态监测相关理论和姿态监测传感器系统，获得半潜式钻井平台在升沉运动过程中的线性加速度随时间的变化规律。参考文献［24］中对平台升沉运动的解算方法，结合姿态监测结果式（18）和式（16）通过一次积分和二次积分求出相应的运动速度和位移，进一步可得平台升沉运动过程中的实时振动幅值系数。

通过姿态监测系统测量得到的平台升沉运动振动幅值系数，可得到半潜式钻井平台在外界环境载荷作用下的升沉位移，该位移数值可作为升沉补偿装置启动补偿动作的输入值，提高半潜式钻井平台升沉运动的补偿精度和反应灵敏度。

同时，由于环境载荷大小和方向的不确定性，在升沉运动平面内导致钻井平台产生复杂的随机振动，该振动会引起钻井平台上其他部件的附加载荷，并使井下处于工作状态的钻头对井底岩石的钻压稳定产生改变，从而影响整个海上钻井系统的疲劳强度寿命和钻井工作的高效进行。在海洋钻井作业中，特别是深海钻井，实时掌握平台的姿态信息和升沉运动规律对保证钻井系统的安全运行具有十分重要的意义。

3　结 语

1） 基于姿态监测相关理论和监测传感器，建立起一套半潜式钻井平台在受复杂海洋环境载荷作用时的姿态监测系统，该系统由数据采集、传输、处理和输出3部分组成；

2） 对钻井平台姿态数据的采集过程中，使用UKF无损滤波算法对传输电路中的干扰信息进行过滤处理，可提高平台非线性系统姿态测量的稳定性和精度；在姿态数据求解运算过程中，使用四元数收敛算法将传感器所测的欧拉角坐标体系转化为四元数坐标体系，避免了平台姿态信息表达过程中因测量角度变化较大时，产生的奇异化现象对测量精度的影响；对半潜式钻井平台的基本运动参量进行解算，得到平台在做纵荡、横荡和升沉运动时三轴向加速度分量；

3） 该监测系统所使用理论成熟，监测系统中各传感元件可靠性高，传输测量过程中所使用算法较合理，使该系统对浮式钻井平台的姿态数据监测，特别是升沉机理的研究及后续补偿装置研发具有一定的理论支撑和数据支持作用，具有较好的实际运用前景。

［1］ Shneider W P. Dynam ic positioning systems［C］//Offshore Technology Conference. Offshore Technology Conference， 1969.

［2］ Moulin P. Automatic Dynamic Positioning System：U.S. Patent 3，500，025［P］. 1970-03-10.

［3］ Balchen J G， Jenssen N A， Mathisen E， et al. A dynamic positioning system based on Kalman filtering and optimal control［J］. 1980：135 -163.

［4］ Hvamb O G. A new concept for fuel tight DP control［C］//Proceedings of the 1998 Dynamic Positioning Conference， Houston，Texas， USA， 2001.

［5］ Kongsberg Maritime A S. Product description-Kongsberg K-Pos DP dynamic positioning system［J］. 2006：96-104.

［6］ 赵建亭. 深水半潜式钻井平台钻井设备配置方案的探讨［J］. 上海造船， 2009 （4）：45-48.

［7］ Edwards R， Johnson T， Campman C， et al. Review of 17 real-time， environment， response， and integrity monitoring systems on floating production platforms in the deep waters of the gulf of mexico［C］// Proceedings of Offshore Technology Conference. Houston， USA：OTC， 2005：1-16.

［8］ 屈 衍，季顺迎，时忠民. 海洋深水浮式平台现场监测研究进展［C］//中国海洋学会海洋工程分会. 十五届中国海洋（岸）工程学术讨论会论文集（上）. 江苏：中国海洋学会海洋工程分会，2011，48-55.

［9］ 毕 盛，闵华清，李 淳，等. 姿态传感器采集测试系统的设计与实现［J］. 计算机测量与控制，2011，19（7）：1562-1564.

［10］ 付 旭，周兆英，熊沈蜀，等. 基于 EKF的多MEMS传感器姿态测量系统［J］. 清华大学学报：自然科学版，2006，46（11）：1857-1859.

［11］ 李东亮. 深水半潜式钻井平台锚泊定位系统调试工艺研究［J］. 船舶与海洋工程，2013（2）：71-75.

［12］ 张会新，王世昌，杨运良，等. 全加速度计惯性测量系统角速度解算方法的优化［J］. 中国惯性技术学报，2008，16（6）：672-675.

［13］ Gulmammadov F. Analysis， modeling， and compensation of bias drift in MEMS inertial sensors［C］ // Recent Advances in Space Technologies. RAST'09. 4th International Conference on. IEEE， 2009.

［14］ 袁广民，李晓莹，常洪龙，等. MEMS 陀螺随机误差补偿在提高姿态参照系统精度中的应用［J］. 西北工业大学学报，2008，26（6）：777-781.

［15］ 蔡志武，赵东明. UKF滤波器性能分析及其在轨道计算中的仿真试验［J］. 武汉大学学报：信息科学版，2006，31（2）：180-183.

［16］ 彭东亮，文成林，薛安克. 多传感器多源信息融合理论及应用［M］. 北京：科学出版社，2010.

［17］ Marins J L， Yun X， Bachmann E R， et al. An extended kalman filter for quaternion-based orientation estimation using MARG sensors［C］// Intelligent Robots and Systems. Proceedings. 2001 IEEE/RSJ International Conference on. IEEE， 2001.

［18］ 刘海颖，王惠南，刘新文. 基于 UKF 的四元数载体姿态确定［J］. 南京航空航天大学学报，2006，38（1）：37-42.

［19］ 刘海颖，王惠南. 低成本姿态测量系统研究［J］. 南京理工大学学报：自然科学版，2007，31 （2）：233-237.

［20］ 张 帆，曹喜滨，邹经湘. 一种新的全角度四元数与欧拉角的转换算法［J］. 南京理工大学学报，2002，26（4）：376-380.

［21］ 刘 忠，梁晓庚，曹秉刚，等. 基于四元数的空间全方位算法研究［J］. 西安交通大学学报，2006，40（5）：618-620.

［22］ 石陆丰，程建生，段金辉，等. 半潜式浮基风电平台设计及波浪动力响应分析［J］. 船舶与海洋工程，2015， 31 （1）：13-19.

［23］ 金鸿章，王 帆，綦志刚. 小型便携式船舶姿态测量系统研究［J］. 仪器仪表学报，2008，29 （7）：1548-1553.

［24］ 方华灿，陈世一. 半潜式钻井平台的升沉运动分析［J］. 石油学报，1986， 7（1）： 83-91.

Research on the Attitude and M otion M onitoring System of Sem i-submersible Drilling Platform

XU Tao1， LIU Qing-you2，LI Wei1

（1. School of Mechanical and Electrical Engineering， Southwest Petroleum University， Chengdu 610500；2. State Key Laboratory of Oil and Gas Geology and Exploration， Southwest Petroleum University， Chengdu 610500）

Aiming to solve the problem of attitude measuring for semi-submersible drilling platform in deep- water oil drilling operation， this study proposes a set of semi-submersible drilling platform monitoring system framework based on attitude monitoring technology， where attitude sensors are used to realize real-time attitude measuring. The problem of accuracy deterioration of three different auxiliary motion sensors — accelerometer， gyroscope sensor and azimuth-angle sensor， caused by signal interfering and expression differences during signal measuring process is solved by UKF filtering algorithm and quaternion algorithm. Basic motion parameters of the sem i-submersible platform can be calculated both on the basis of measured data and the calculated results to obtain the mathematical expression of its three axial acceleration components during surge， sway and heave motions. This attitude monitoring system provides some theoretical and data support for the study of complex platform motion mechanism as well as for the design of heave compensation device， thus to bring an application potential for the system under actual operational conditions.

semi-submersible drilling platform； attitude monitoring； UKF filter； quaternion； offshore drilling

TP216

A

2095-4069 （2016） 02-0038-07

10.14056/j.cnki.naoe.2016.02.008

2015-04-30

国家自然科学基金项目（51274171）；西南石油大学研究生创新基金项目（CXJJ2015016）

徐 涛，男，1989年生。西南石油大学机电工程学院硕士研究生，研究方向为海洋油气装备现代设计与仿真研究。