扫描法在车辆路径问题中的应用

曹茜 文乔

摘 要：随着经济的高速发展，物流行业发展也进入了加速前进的步伐中，而想要在加速前进中不被时代落下，就必须不断优化物流环节，使总成本达到最小化。物流企业往往会在车辆路径的选择方面进行多方面的考虑，文章主要研究了车辆路径问题，它是运筹学和组合优化领域的研究热点问题之一。主要通过扫描法来解决车辆路径问题，其中运用了EXCEL的规划求解方法。同时结合安吉汽车物流有限公司的车辆路径问题的案例，用扫描法给出了相应的最优路径方案。

关键词：VRP模型；扫描法；规划求解

中图分类号：U116.2 文献标识码：A

Abstract： With the rapid development of economy， the development of logistics industry has also entered the pace of accelerating the pace of progress. And we must continue to optimize logistics links， so that the total cost to be minimized and not fall in the era of accelerated advance. The logistics enterprises tend to be considered in the selection operation of the routing. This paper mainly considers the vehicle routing problem， it is one of the hot topics in the field of operations research and combinatorial optimization. The scanning method is used to solve the vehicle routing problem， which includes EXCEL programming solver methods. Meanwhile， the case of the vehicle routing problem for Anji automotive logistics company is given， and the optimal routing is obtained by using scanning method.

Key words： vehicle routing problem； scanning method； programming solver

0 引 言

在物流企业中，物流运输的成本几乎占了整个物流环节的一半，为了获取更加可观的利益，企业往往会在运行线路的选择方面进行多方面的考虑，由此引申出了车辆路径问题。

车辆路径问题（Vehicle Routing Problem， VRP）是1959年[1]由Dantzig和Ramser提出的，它一般是指对一系列装货点和卸货点，在对一定的约束条件（如货物的需求量、车辆的容量限制等）满足的情况下，组织安排合适的行车路线，使合理的车辆能够有序地通过它们，达到一定的理想目标（如最短的路程、最少的费用成本、最少的时间成本、最少的车辆使用数等）。本文通过扫描法来对具体的安吉物流有限公司的案例进行分析求解，扫描法最初是由Gillett和Miller在1974年[2]提出来的，它体现的是一种逐次逼近的方法，下面将给出扫描法的具体思路。

1 扫描法

扫描法的基本原理是从最开始出发的供货点向其任意方向的外沿延伸出一条直线，再从这条直线开始通过规定的顺时针或者逆时针旋转方式来进行旋转，这样当旋转完一周回到原来的位置时，所有需要配送货物的点都已经经过，而在配送过程中车辆的承载货物不能超过规定容量，这就形成了分组的办法。

扫描法步骤：

（1）设计一个极坐标系，其中供货点即最开始出发的点被当做极坐标系的原点，再通过将原点与连通图中出现的任意一个需求点相连的线的角度作为零度。在极坐标系中准确找到每一个需求点的位置，并将其通过计算得出相应度数来转换成极坐标系。

（2）对全部需求点进行分组。从零度即最小角度的需求点开始，设定一个需求点的集合，然后按照逆时针的方向，依次旋转将需求点加入到那个集合内，当需求点的需求量累计超过了车辆规定的容量时，这个集合将不再允许加入新的需求点，从而建立一个新的需求点集合，继续逆时针旋转，对需求点进行收集。

（3）重复之前的步骤（2），直到所有的需求点都已经加入到不同或者相同的组合中为止。

（4）路径优化。当所有的分组结果已经出现的时候，对于每一个组的需求点而言，将变成独立的旅行商问题（Traveling Salesman Problem，TSP），这就需要进行TSP模型分析优化，从而得出一个较合理的优化路线。TSP问题可以描述如下：在已知的一个具有n个顶点且其中线路连接方式可以有向或无向的网络中，被要求通过计算找出一个闭合回路，这个闭合回路必须由起点出发经过所有的顶点后再回到起点。本文用EXCEL的规划求解功能来求出相应的TSP模型的解。

2 建立模型

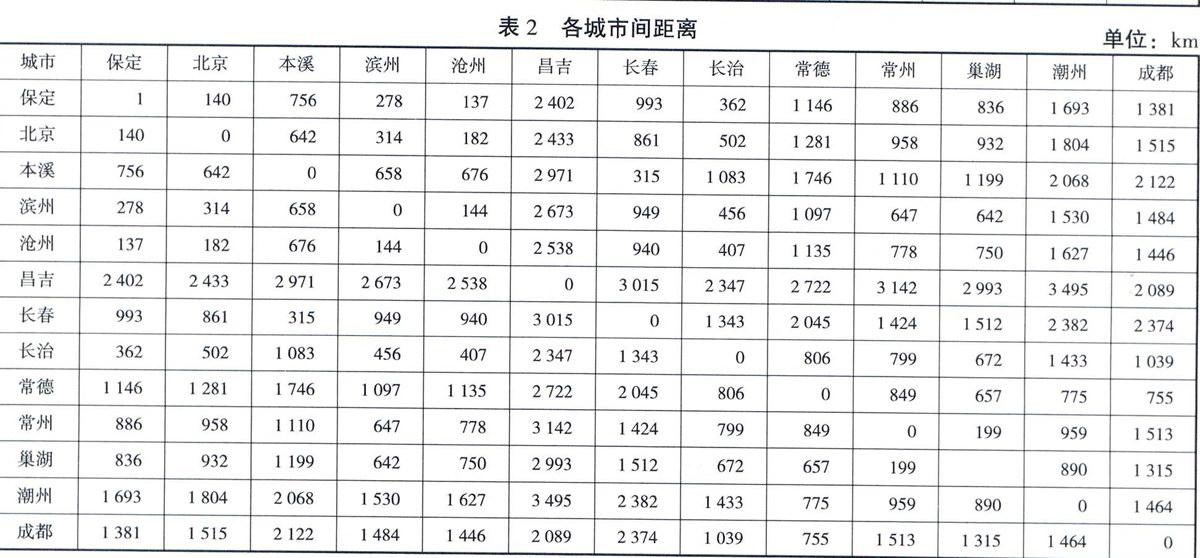
安吉汽车物流有限公司成立于2000年8月，是上汽集团旗下的全资子公司，它为上海大众汽车提供稳定的配送服务。大众汽车根据各城市之前月份的销售记录，对下一个月的销量进行预测，并且制定出了下一月份需要安吉物流配送的运输订单量，而安吉物流在接到订单开始，将需要制定出一份详细的配送路线，使运输成本最低，以达到利润的最大化。其中配送供应点为滨州，目前一次能够配送的能力不超过330千辆，而需要进行配送的地区的需求量和每个地区间的距离分别如表1和表2所示。

3 利用扫描法求解

（1）建立极坐标系，其中以滨州作为极坐标系的原点，得出表3：

（2）对全部需要配送的城市进行分组。首先从零度开始，进行逆时针旋转扫描，可以通过对位置图的观察了解到，第一个被分组的城市是本溪，此时配送量Load1为36千辆；继续旋转，下一个被分组的是长春，此时Load1=36+63=99千辆，而因为配送量还未超过一次性允许配送的荷载能力，故继续旋转；下一个被分组的是北京，此时Load1=36+ 63+20=119千辆<330千辆，继续旋转；下一个被分组的是沧州，此时Load1=36+63+20+52=171千辆<330千辆，故继续旋转；下一个被分组的是保定，此时Load1=36+63+20+52+30=201千辆<330千辆，故继续旋转；下一个被分组的是昌吉，此时Load1=36+63+20+52+30

+55=256千辆<330千辆，故继续旋转；下一个被分组的是长治，此时Load1=36+63+20+52+30+55+65=321千辆<330千辆，故继续旋转；下一个被分组的是成都，此时Load1=36+63+20+52+30+55+65+86=407千辆>330千辆，所以停止旋转，第一个分组已经得出结果，即第一组内需要经过的城市有本溪、长春、北京、沧州、保定、昌吉、长治七个城市。重复以上步骤，可以得到第二个组内的城市为成都、常德、潮州、巢湖、常州五个城市。

（3）通过以上的计算，安吉物流可以安排分别两个不同的路径对需求城市进行配送，其中两个路径中包含的城市分别为：

T■=本溪、长春、北京、沧州、保定、昌吉、长治；

T■=成都、常德、潮州、巢湖、常州。

（4）分别对两个组的车辆运行路线即TSP问题进行规划求解。

①对第一组城市进行规划求解。首先在EXCEL中输入城市间距离矩阵的数据，如图1所示：

再建立连通状态矩阵如图2，其中每一个城市间的连通状态由二进制来表示，即连通表示为1，不连通表示为0，将最初输入的值都设定为0，而因为每一个城市都需要进行配送，所以城市经过的次数为1，需要注意的是城市经过的次数为矩阵中对应城市所配送经过的总和；此外相同的一个城市不能相连，即对角线不能为1。

而为了防止两个城市之间双向互连，输入了一个矩阵如图3，其中的数值为连通矩阵图中对应的两个城市间的双向连通情况之和，而这个和必须小于或者等于1，例如保定到北京的数值等于连通状态矩阵中北京到保定与保定到北京的连通状态之和。

根据设定连通顺序的限制条件，如图4，其主要原理为：

接入点的顺序-接出点的顺序+N（城市总个数）*所求两点间的连通状态（1为连通、0为不连通）<=N-1，根据这个原理，在EXCEL中输入公式，进行计算。

由于目标函数为各城市的连通顺序与连通状态，所以还需要设计条件所求的连通顺序为整数，且在最小数1和最大数8（城市总数）之间。而在这里还需要设置一个目标，即最小总路程，最小总路程==SUMPRODUCT（距离矩阵，连通矩阵）。

最后将上述的条件都设定完成，通过规划求解，如图5所示。

得到的结果如图6所示。

故规划求解得出的第一组城市的配送路径为：滨州→沧州→北京→本溪→长春→昌吉→长治→保定→滨州，该路线的总里程为7 285km，配送货物总量为321千辆。

②用上述方法对第二组城市进行规划求解，得到第二组城市的配送路径为：滨州→成都→常德→潮州→巢湖→常州→滨州，该路线的总里程为4 750km，配送货物总量为274千辆。

4 结束语

本文阐述分析了扫描法在车辆路径问题中的运用，同时对安吉汽车物流有限公司的车辆路径相关问题建立了模型，并通过扫描法及使用EXCEL的规划求解功能给出了最终求解方案，从而达到路径优化的目的。

参考文献：

[1] Dantzig G， Ramser J. The truck dispatching problem[J]. Management Science， 1959（13）：80-91.

[2] Gillett BE， Miller LR. A heuristic algorithm for the vehicle dispatch problem[J]. Operations Research， 1974（22）：340-349.