小学生数学学习中的“想当然”现象剖析及对策

魏晓敏

摘要：小学生数学学习中出现的一些“想当然”式的错误和学生的认知水平与认知方式有关，更和教师的课堂教学方法有关。教师要善待学生出现的错误，把错误当做研究学生的宝贵教学资源，具体问题具体分析，提升学生解读问题与正确解题的能力。

关键词：数学学习；“想当然”式障碍；对策与改进；主动参与；探究

在任何一种学习过程中，由于学生受生理、心理特征及认知水平的限制，会出现很多“想当然”式的错误。所谓“吃一堑，长一智”，这些错误的产生是有其背后原因的。对于错误的原因，如果在本质上得不到探查，错误只能是错误，而永远得不到纠正，甚至把错误在不断练习在得到“巩固”，那就十分可怕了。

一、小学生解题中“想当然”现象及其成因

（1）教师方面

一个难以改变的现状是“灌输式教学涛声依旧，探究式教学仅成摆设”。由于受传统思维和考试分数的牵制，不少课堂教学模式基本上是灌输——接受，学生学习方式基本上是听讲一背诵——练习——再现教师传授的知识。如有的学生牢记π=3.14，2π=6.28，3π=9.42，4π=12.56，由于教师引导他去记住以便提高计算速度，故不断强化的训练使他对π=3.14深信不疑。可是他竞不知道π是怎么产生的，其确切值并不等于3.14，比如填空题：一个圆的半径扩大3倍，则直径扩大（）倍，圆面积扩大（）倍，圆周率（）。他就会无所适从而在最后一格填上“扩大三倍”。

数学知识获得经验不仅是实践的经验，不仅是解题的经验，更重要的是思维的经验。假如教师在教学的课堂上不是直接告诉学生知识，而是注重让学生观察、操作、动手实践，自主探究，也许就不会出现这种情况了。

另一种不良倾向在计算教学中过分重视算法的总结而忽视基本算理的提炼。在新课标的理念指导下，教师们认识到了原有教学模式的局限，大张旗鼓地开展自主学习，发挥学生的学习主动性。在计算教学中过分强调计算方法的多样化，以至于课堂上遍地都是“你是怎么想的”、“还有其他不同的算法吗”、“你喜欢怎么算就怎么算”。看起来对学生的思考比较尊重，却没有真正将学生的思维纳入算理探究的深处。

（2）学生方面

新课程改革后，教材删除了一些比较烦琐的计算题，计算难度大大下降，却对计算能力与解题品质的要求更高了。我们在批改作业时都会发现，有很多学生并不是不会做计算题，而是会做而做不对。有时我们想了解学生错误的原因，让学生再做一遍，学生也能做对。作为教师必须认真分析错误原因，制定对策，减少错误率。比如有的在横式计算中由于没打竖式直接口算，做完又没有检查，就会错误百出；也有的是计算时抄错数字或运算符号，从而造成计算错误，如把54抄成45，把“×”抄成“+”，再如：5.5+4.5=1，2.4+3.2=6.6，从学生的心理角度来看是属于小学生感知比较粗略造成的。

其一，受心理发展水平制约。小学生感知事物不仔细、不全面，比较笼统、模糊，只能感知客体的个别部分，而且感知的目的性较低，他们一般还不会独立地给自己提出感知任务。这就造成学生对题意理解不全面，不精细，造成抄错数字或漏写数字等。

其二，缺少认真负责、一丝不苟的学习态度。看图读题一扫而过，了解个大概题意，凭感觉走；计算不论数的大小，能口算的全部口算，有的虽有草算，但写得乱七八糟，有些学生一次练习或测验下来连一张草稿纸都没有，而直接写在试卷旁边，更有甚者写在桌面上……思想上的不重视，必然导致计算上的经常出错。

其三，缺少计算后必须检验的内控心理素养。其中一些学生学习过于自信，计算后从不检验；而有一些学生只想作业尽快完成，根本就不想检查；更有一些学生知道自己无把握全部正确，就依赖于家长代为检查或等教师批改后，有错再订正。由于上述这些不正确的心态，许多学生就养成计算后不检查的坏习惯。

其四，有一定坡度的题目，学生对题意不能理解，抽象思维或空间想象能力不够，从而造成列式错误。

二、针对学生理解障碍的解决策略

1.强化读题，完整获取信息

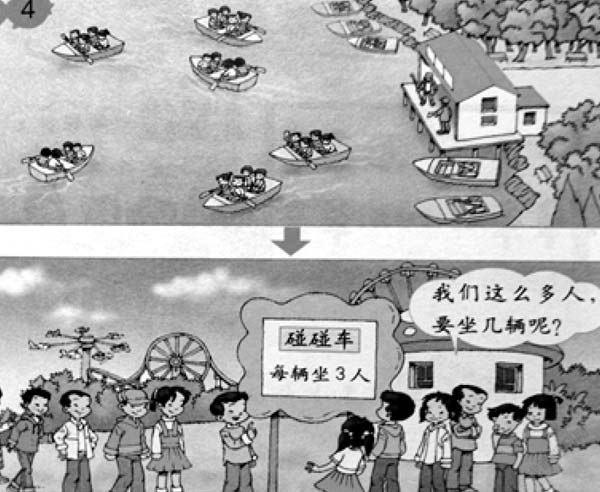
例1 （如图）学生出现了两种算式：12÷3，24÷3。

教师适时引导，提醒学生读懂一句话就可以。

师：图上说“我们这么多人”指哪些人呢？请大家再次看图并思考，并在小组里说说想法。

生1：第二个算式正确。因为他们先划船，用4×6=24（人）就能求出共有多少人：再坐碰碰车，要24÷3=8（辆）。

生2：图上有个箭头，说明他们先划船再坐碰碰车，划船的人就是坐碰碰车的人。

生3：如果只有12人，只要下面这幅图就好了。

所以学生在解答应用题时，首先要在教师的指导下，通过找出关键词或句，选择正确的解法，培养学生认真审题的习惯。

2.着眼比较，学会转换思考

倒2 一个长和宽都是20 cm，水深15 cm的水箱里放进一块石头，结果水面上升2 cm，这块石头的体积是多少？

学生算成：v=abh=20×15×2=600（立方厘米）

于是教师又出示了这样一道题：一块长方体石头的长与宽都是20 cm，高是2 cm，请问它的体积是多少？学生就明白了刚才的列式是错误的。

出示数学问题后，学生内心的第一个问题应该是：“我可以从题目知道些什么？”通过对题目中所有信息的还原，在脑海或者草稿本上形成相关数量关系。在这一题的解答过程中，学生要学会把所求问题转换为水面上升的体积，就能通过计算上升水的体积来达到目的。

3.依托图示，提升表征能力

例3 钱塘江全长约605千米，比曹娥江的3倍还多59千米，曹娥江全长多少千米？

错误解答：605×3+59=1874（千米）。

小学生的思维方式以直观形象思维为主，抽象思维能力还不强。由于我们教师过度强调“倍数”与“多”字的意义而误导了学生，使学生受到思维负迁移作用的影响。

借助画图，可以把抽象的知识变成形象的知识，因此，当学生遇到有一定思维难度的题目时，教师就要结合实物模型直观演示，借助画图等方法，逐步引导学生进行分析思考，发展抽象思维能力，提升思维水平。

4.抓实抓细，培养良好习惯

针对小学生的这种心理特点，我们应注意重视首次感知，激发学生的学习积极性。教学中，为学生提供准确、生动、鲜明的首次感知材料，突出学生容易忽略的部分，加强其刺激强度。在作业批改方面，要尽量挖掘他们的优点，评价从宽；对于他们的不足处，要正面引导。如对每次作业应用红笔做出肯定的标志，如用“√”“优”等，定期展示班级学生的学习成果，对于每个学生的进步予以及时的肯定和精神奖励等。让他们体验到成功的快乐，从而不断地培养学习兴趣。

笔者还要求每个学生要有一本草稿簿，打草稿时要求他们书写工整。我们还经常不定时检查学生的草稿簿，表扬书写工整、准确认真的学生，促进学生养成良好的书写、打草稿的习惯。

我们认为，小学生解题中的“想当然”现象的成因主要还在于学习态度上的任意性，思考方式上的粗糙性与不求甚解，还有解题习惯上的随便性。但也说明了小学生在阅读理解能力、综合分析能力还处于较低层面。教师要善待学生出现的错误，把错误当做研究学生的宝贵教学资源，具体问题具体分析，认真剖析原因，有针对性地引导，从而培养起学生良好的学习习惯与思维方式，为今后的高效学习服务。