Louvain算法的并行化处理

吴卫江　李沐南　李国和

(中国石油大学(北京)地球物理与信息工程学院　北京　102200)



Louvain算法的并行化处理

吴卫江李沐南李国和

(中国石油大学(北京)地球物理与信息工程学院北京102200)

社团结构作为复杂网络的一个重要特征,被广泛应用到物理、生物、计算机以及社会学等领域。在实际应用中,社团发现算法的效率与社团划分结果的准确性对挖掘网络特性十分关键。Louvain算法是一种基于模块度的快速凝聚算法,能够准确划分出层次社团。在研究Louvain算法的基础上,针对算法主要耗时在计算模块度与遍历模块度增量上的问题,提出并行化的处理方法改进算法的运算效率,并应用改进后的算法在分布式系统上处理包含上千节点的Facebook数据集,通过对比原算法的运行结果,发现在社团划分效果准确的基础上,改进的并行化算法效率更优。

社团发现; Louvain; 并行化; 效率; 分布式系统

Class NumberTP301.6

1　引言

复杂网络是由数目巨大的节点构成的网络拓扑结构,节点间关系复杂。现实中存在着不同种类的复杂网络,如社会学中的人际关系网、生物学中的神经元网、计算机学中的科学引文网等。目前复杂网络作为重要的多学科交叉研究领域之一,对其进行研究具有重要的理论意义和广泛的应用前景。

社团结构是复杂网络的一个重要特征,大量研究表明许多现实网络都拥有自己的社团结构,而不是一大批节点随机连接在一起,这种结构表现在社团内部节点联系紧密,而社团之间节点联系稀疏[1]。研究社团结构有助于人们理解复杂网络的结构与特性。

经典社团发现算法主要有两大类,一类是计算机学中的图形分割,另一类是社会学中的分层聚类。计算机学中的图形分割著名的两个算法是K-L算法和基于图的Laplace矩阵特征向量的谱平分法;社会学中的分级聚类是基于节点之间的相似性[2],把网络划分为不同社团。该算法又可以分为两类:凝聚算法(Agglomerative Method)和分裂方法(Divisive Method)[3]。

为了衡量划分的结果,聚类算法采用模块度作为度量方式,它是指社团结构内部的边数减去随机生成网络中的期望的边数。模块度[3]是基于随机网络没有社团结构的假设为前提,它通过度量网络划分的好坏来度量网络社团结构。由于模块度对社团划分结果的重要性,许多算法都基于模块度进行改进,得到更高效的优化算法。Louvain算法就是基于模块度的一个凝聚算法,相比于其他一些社团发现算法,它的运算速度更快,并且不会出现对小规模社团的探测遗漏现象[4],可应用于节点数目巨大的网络。

本文就是在Louvain算法的基础上进行改进提出并行化的处理方法,提高算法的运算效率,并在分布式系统中实现。

2　Louvain算法

2.1算法思想

Louvain算法是基于模块增量的算法。算法主要分为两个阶段,首先初始化每个节点为一个社团,不断遍历网络中的所有节点,将其从原来的社团取出,计算该点加入到各个社团产生的模块度增量,如果该模块度增量大于零,则从这些大于零的模块度增量所对应的社团中选出对应模块增量最大的社团,将该点与之合并。重复上述过程,直到网络中社团不再合并[5]。其次利用划分得到的第一层社团构造新的网络,新节点之间的权值就是原社团之间的权值。重复上一阶段的过程,直到社团之间不能再合并为止。

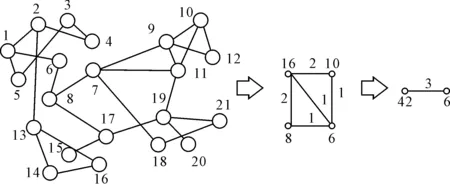
图1　Louvain算法过程

2.2评价模型

1) 模块度

社团模块度指标Q是用于刻画社团性强弱的参数,定义如下[6]:

(1)

式(1)中,ki和kj是节点的度值;Ci是节点i所属社团;m是网络总边数;Aij代表了节点i与节点j之间的边的权值;δ(Ci,Cj)函数表示节点i与j在同一个集群内,当Ci=Cj时,δ(Ci,Cj)=1,否则为0。Q值在[0,1]之间,一般以Q=0.3作为网络有明显社团结构Q值越接近1,说明发现的社团质量越高。

2) 模块度增量

首先进行社团初始化,网络中的每个节点都分配一个社团编号,初始时每个节点都看作一个社团,对应社团的模块度增量ΔQ[7]:

(2)

其中∑in是社团内部边的权值之和;∑out是所有与社团内部节点相连的边的权值之和;ki是所有与点i相连的边的权值之和;Ki,in是节点i与社团C相连的边的权值之和。

3　算法的并行化处理

3.1改进思想

通过对Louvain算法的研究发现,算法主要耗时在计算整个图的模块度与遍历每个点计算该点到不同社团的模块度增量上,模块变量决定相连节点是否可以合并到一起,而模块度决定运算是否停止,所以需要多次计算模块度和模块变量。而在整个Louvain运算中,该处的运算是最消耗时间和计算机内存的。因此可以进行如下改进。

1) 模块度计算的并行

表1　模块度并行思想演示

图的模块度计算是需要使用到各个节点的内部边数(只和自身相连的边),外部边数(和其他点相连的边)。对于各个节点,可以使用并行化的进行处理。最后可以将得到的数据相加得到整体的模块度。

2) 模块度变量的并行化处理

计算两个节点i,j的模块变量的时候,需要计算i,j之间的边数,i的外部边数减去i和j之间的边数(i和i的相连节点中除去节点j之后的边数),j的外部边数减去i和j之间的边数(j和j相连节点中除去节点i之后的边数)。在计算每个节点的模块变量时,记录模块变量最大的邻居节点。如果该节点大于0,则把这两个点合并为一个社区。

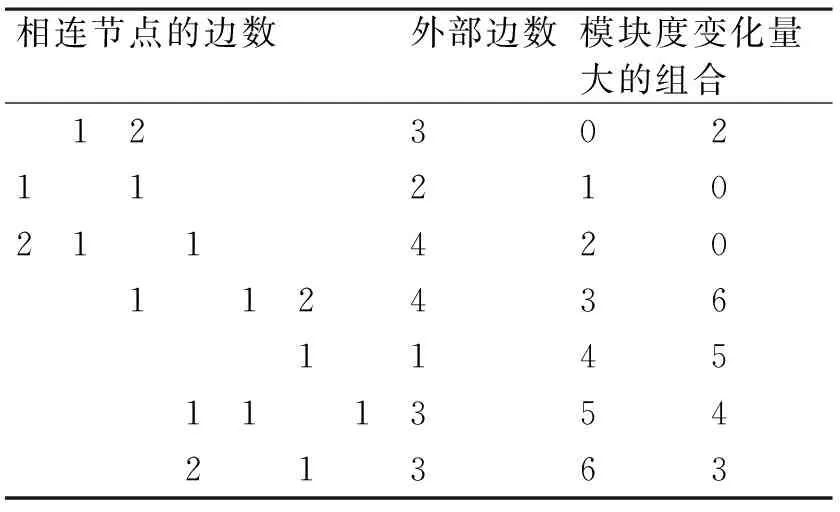
表2　模块度变量并行算法演示

3.2处理过程

由于本算法将用于数据量巨大的图,所以使用二维映射图将连接表相连节点和对应的边数进行处理。同时为了不影响计算速度,对于计算量较大的模块度增量,使用矩阵向量进行处理。下面列出并行化[8]思想的基本过程:

1.while Q_new > Q_old do

2.Q_old = Q_new

3.parallel foreach v in V

4.将v中ΔQ最大的节点加入V

5.end foreach

6. Vq和V中的节点进行合并

7.基于En,Ei构成一个新的图

8.(更新En,Ei,Eo,V)

9. Q_new = 0

10.parallel foreach v in V

11.基于Ei,Eo计算Qv

12.Q_new = Q_new + Qv

13.end foreach

14.end while

4　评价实验

4.1实验方法

在Spark[9]上实现并行化算法是一个比较好的选择,Spark立足于内存计算,天然的适应于迭代式计算。同时主要研究Louvain的并行化算法,所以充分利用Spark自带的API可以使研究变的更加简单。只需要了解相关Spark基础知识并且了解聚类算法的原理以及方法相关参数的含义,就可以轻松地通过调用相应的API来实现基于海量数据的聚类过程。当然,原始数据ETL,特征指标提取,调节参数并优化学习过程,这依然需要有足够的行业知识和数据敏感度,这往往也是经验的体现。本节重点在于说明如何使用Spark的分布式运算架构来实现并行化算法并验证效果。

1) 将图中的每一个节点都看成一个独立的社团,并进行编号;

2) 对每个节点i,依次把节点i从原社团中取出并分配到与其相连的邻居节点所在的社区,计算节点i分配到新社区后的模块度变量,并记录模块度变量最大的那个邻居节点,如果模块度变量大于0,就把节点i加入到对应模块度变量最大的那个邻居节点所在的社团,否则保持不变;

3) 重复过程2),直到所有节点所属的社团不再发生变化,此时可以得到一个初始的社团结构;

4) 对整个图的节点进行合并,将处在同一个社团的节点合并成一个新节点,社团内节点之间的边的权值转化为新节点的环的权值,社团间的边权值转化为新节点间的边的权值;

5) 重复过程1),直到整个图的模块度不再发生变化。

4.2分布式具体实现过程

1) 获得邻居节点信息

(MapReduceTriplets)

其中,Map:生成邻居节点的消息VertexData;Reduce:获得所有邻居节点的信息(Id,Array[VertexData])。

2) 获得每个节点新社区〈Id,getBestCommunity(Array[VertexData])〉。

3) 更新图信息,合并节点并进行多轮迭代。

在算法的第2)步中,节点i的社区变更会在节点i+1的社区分配时可见,但在分布式系统上实现很难保证这一点,因为在分布式环境下,无法预测到哪个机器的计算会率先完成,节点i和节点i+1的社区变更可能是在不同机器上同时进行,不能进行实时传递,因此在分布式系统中实现并行算法时,会出现消息滞后[10]的现象,为了解决这个问题,需要设计使用节点id和和社区id构成的边来组成新图,再用连通图来调整节点的社区,来保证节点所在社区号基本保持不变。

4.3实验数据集

我们所用到目标数据集是来自Stanford Large Network Dataset Collection(SNAP)的Social networks。SNAP是一个关于社团分类算法测试数据的下载中心站点,里面包含了适用于做聚类、分群、回归等各种来自于各个社区网站的的数据集,比如Facebook、Twitter等。

4.4实验过程

使用改进后的并行化算法和未改进的Louvain算法来对上文中的FaceBook数据集进行分析来验证算法效率和精确度。

未改进的Louvain算法的运算结果如下所示:

Number of nodes: 40552

Number of edges: 956872

Running Louvain algorithm...

Random start: 1

Iteration: 1

Modularity: 0.9261

Iteration: 2

Modularity: 0.9296

Iteration: 3

Modularity: 0.9296

Random start: 2

Iteration: 1

Modularity: 0.9265

Iteration: 2

Modularity: 0.9301

Iteration: 3

Modularity: 0.9301

Maximum modularity in 2 random starts: 0.9301

Elapsed time: 34 seconds

可以看到未改进的Louvain算法在运行40552个节点的数据时候需要34s且得到的模块化变量最优值是0.9301。

为了有效提升社团算法的运算速度,实验利用了Spark分布式计算系统,将实验数据上传至服务器,在使用分布式计算时,使用的是HDFS储存数据文件,运行程序之前我们需要提前把数据文件上传到HDFS[11]。程序命令如下:

hdfs://〈hdfs_namenode_ip〉:9000/user/fams/mllib/facebook_combined.txt

Louvain并行化算法的运行结果如下所示:

Number of nodes: 40552

Number of edges: 956872

Running Louvain algorithm on spark...

Random start: 1

Iteration: 1

Modularity: 0.9264

Iteration: 2

Modularity: 0.9298

Iteration: 3

Modularity: 0.9298

Random start: 2

Iteration: 1

Modularity: 0.9261

Iteration: 2

Modularity: 0.9296

Iteration: 3

Modularity: 0.9296

Maximum modularity in 2 random starts: 0.9298

Elapsed time: 13 seconds

图2为来自具有40000个节点的Facebook数据集的社团分类实现结果,算法能够将网络分为几个明显的社团结构。

图2　具有40000个节点的社团分类实现结果

如以上结果所示,并行化算法在时间性能上有了较大提高,这是因为在计算节点时我们充分利用了并行化计算在迭代上的优秀表现,并结合分布式运算模型,极大地节约了运算时间,同时在运算结果上也能得到预期值。

5　结语

本论文主要对在已经存在的聚类算法中需要进行大量计算的过程提出并行计算方法并解释了相关的算法。对该算法进行实验测试对比运行效率。

社交网络等一些复杂网络都是不停地在进行数据更新,对于这样的网络图应该提出怎样的动态聚类算法也是接下来应该讨论的问题。同时,本文基于louvain算法提出的并行化算法,但是由于并行化计算的过程具有不可预期性,虽然针对计算过程中的延迟问题提出了连通图的方法,但期待接下来有更好的算法来优化并行化算法。

[1] 汪小帆,刘亚冰.复杂网络中的社团结构算法综述[J].电子科技大学学报,2009(5):537-543.

WANG Xiaofan, LIU Yabing. Journal of the complex network community structure algorithms[J]. University of Electronic Science and Technology,2009(5):537-543.

[2] Newman M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E,2004,69(6):066133.

JIE Zhou, WANG Xiaofan. The researchof community structure in complex networks analysis algorithm[J]. Complex Systems and Complexity Science,2005(3):1-12.

[4] Blondel V D, Guillaume J L, Lambiotee R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics: Theory and Experiment,2008(10):P10008.

[5] Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences,2002,99(12):7821-7826.

[6] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E,2004,69(2):026113.

[7] Palla G, Derényi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature,2005,435(7043):814-818.

[8] Katoh K, Toh H. Parallelization of the MAFFT multiple sequence alignment program[J]. Bioinformatics,2010,26(15):1899-1900.

[9] Zaharia M, Chowdhury M, Franklin M J, et al. Spark: cluster computing with working sets[C]//Proceedings of the 2nd USENIX conference on Hot topics in cloud computing,2010:10-10.

[10] Dean J, Ghemawat S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM,2008,51(1):107-113.

[11] Berendsen H J C, van der Spoel D, van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation[J]. Computer Physics Communications,1995,91(1):43-56.

Parallel Processing of the Louvain Algorithm

WU WeijiangLI MunanLI Guohe

(College of Geophysics and Information Engineering, China University of Petroleum (Beijing), Beijing102200)

Community structure is an important property of complex networks, which is widely used in the fields of physics, biology, computer and sociology. In a practical application, the efficiency of the community detect algorithm and the accuracy of the results are very important. The Louvain algorithm is a clustering algorithm finding hierarchical community structure based on the modularity function, which has good efficiency and accuracy. Based on the research of the Louvain algorithm, the parallel processing method is used to find a more efficient algorithm. And the data set is processed with thousands of nodes by using the Louvain algorithm and the improved algorithm on the distributed system, it is found that the improved algorithm is more efficient by comparing the running results.

community detect, Louvain, parallel, efficiency, distributed system

2016年2月9日,

2016年3月14日

国家自然基金项目(编号:60473125)资助。

吴卫江,男,硕士,副教授,研究方向:数据挖掘。李沐南,女,硕士研究生,研究方向:数据挖掘。李国和,男,博士,教授,研究方向:数据挖掘。

TP301.6

10.3969/j.issn.1672-9722.2016.08.002