考虑网络交互影响效应的评价者权重分配方法①

李永立， 吴　冲， 张晓飞

(1. 东北大学工商管理学院， 沈阳 110169； 2. 哈尔滨工业大学管理学院， 哈尔滨 150001)



考虑网络交互影响效应的评价者权重分配方法①

李永立1， 吴冲2， 张晓飞2

(1. 东北大学工商管理学院， 沈阳 110169； 2. 哈尔滨工业大学管理学院， 哈尔滨 150001)

确定评价者的权重是评价理论与方法重要的一步. 提出了基于网络博弈框架的新的评价者权重分配方法，并就解和参数的性质进行了详尽的讨论与验证. 将评价者视为网络节点，评价者的评价行为形成评价者之间的联系，构成网络的边，根据评价者的评分信息定义他们之间的“合作”和“冲突”矩阵构成网络的权重矩阵，建立了网络博弈的模型，其最优解即为权重值. 给出了模型最优解的求解方法，并证明了该最优解是Nash均衡的内点解，并且是这一问题唯一的Nash均衡解. 分析了最优解与网络中心性测度之间的联系，较为本质地分析了最优解在网络科学中的含义，将决策理论与网络科学的知识关联起来. 通过数学证明和仿真分析，揭示了模型中参数的含义，其对于解的“保序性”和“稳定性”两个优良性质是此消彼长的关系，提出了根据数据集特征选择参数值的相机抉择的管理思想；并在真实的数据集上进一步做模型的应用分析. 本文提出的考虑网络交互影响效应的权重分配方法具有实用性，能够平衡解“保序性”和“稳定性”两个良好属性，具有理论意义和实践价值.

评价理论与方法; 优化模型； 网络分析； 交互效应； 网络博弈； 权重分配； 仿真

0　引　言

评价理论与方法的研究是管理科学与工程领域重要的研究分支，其联系着理论模型的构建[1-3]，丰富决策理论与方法的知识体系，同时涉及广泛的应用，是管理实践工作中较为广泛采用的管理方法之一[4-6]. 注意到评价结果直接受到评价者或决策者权重的影响，其反映了各个评价者和决策者的重要性程度，关系到评价结果的可靠性和可信性，因此，评价者的权重分配问题是管理决策和评价过程一个重要的环节，本文集中分析这一问题，拟提出一个具有良好性质的评价者权重分配方法，扩展领域知识，丰富管理实践.

确定评价者的权重问题一直被相关领域的学者所关注，按照年代顺序，这一领域的研究工作有如下文献：French[7]利用图论处理决策成员之间的相互影响关系，由这一影响关系确定广告成员的重要性；Bodily[8]利用除去某成员之外的决策群体投票的方法来获取该决策者的权重；Mirkin等[9]将特征向量引入决策者权重确定中，建立了基于向量的权重分配方法；Brock[10]利用纳什谈判的方法来估计一项群体决策中各个决策者的权重；Ramanathan和Ganesh[11]在决策群成员主观意见的基础上，利用特征向量进行处理，从而求得各个成员的权重；宋光兴和邹平[12]分别给出了AHP判断矩阵和排序向量下的决策者客观权重确定方法，并提出由主观权重和客观权重结合确定最终权重的方法；Honert[13]将层次分析法和Smart模型相结合，形成了REMBRADT决策者赋权系统；徐泽水和达庆利[14]在兼顾主观权重信息和客观权重信息的基础上，利用线性目标规划建立了多属性决策组合赋权方法，以及Xu[15]利用多种类型的语言偏好关系来决定决策者权重；Yue[16]在TOPSIS方法的基础上解决多属性群决策问题时，利用个人决策和理想决策之间的欧几里德距离来决定决策者之间的权重分配问题，以及Yue和Jia[17]利用一个扩展的TOPSIS方法解决区间值直觉模糊环境下的决策者权重分配. 纵观以上文献，可以发现以上的权重确定方法并没有考虑网络的交互影响效应，也鲜有文献从网络博弈的角度确定评价者的权重，本文将从这些思考点出发，提出新的权重确定方法，并通过数学证明和仿真分析的技术手段，论证本文提出新方法的有利特征；特别是本文重点分析了模型的假设，指出了新发法的适用范围. 从学科体系上说，本文的方法和以上文献同属于一个学科领域，是相互补充的关系；从发展的角度看，本文的方法也是以上方法的发展和有利补充，并进行了较为完整地论证，而不是仅仅局限于个别算例的分析.

由此，本文的主要工作及贡献如下：1)将评价者(决策者)的权重分配问题视为一个网络博弈问题，构建网络模型考虑了评价者之间的相互影响效应：也即“合作”与“冲突”的关系，建立了描述该网络博弈问题的最优化模型；2)讨论了模型最优解的相关性质，并将其与网络中心性测度的理论统一起来，挖掘了该决策问题与网络中心性测度的内在联系；3)证明了基于模型的最优解是Nash均衡的内点解，并且是这一问题唯一的Nash均衡解；4)给出了模型参数的取值范围，并探索了参数的不同取值对最优解“保持既有评价序”和“当存在虚假数据时，解鲁棒性”两个性质的影响关系问题，显然一个优良的评价结果应当具有既能“更多地反映既有评价者的评价序关系”，又能“在存在虚假数据时，保持解的稳定性”这两方面的能力；5)在真实数据集上，做了模型的应用工作. 为此，本文以下的各节按照以上“工作及贡献”呈现的顺序逐步展开，并在总结部分就全文的工作和意义做了一个更详尽的表述.

1　模型及其意义

1.1基于网络视角的权重分配模型构建

不失一般性，一个评价系统可以抽象为如下的模型：该系统中有n个评价者，他们对m种商品(或者是服务)中的全部或者部分做出评分. 当第i个评价者对第s种商品做出评分时，该评分记为vis，当没有做出评分时，记为“—”；其中，i∈{1,2,…,n}，s∈{1,2,…,m}，vis可以为任意实数，但一般情况下，vis≥0.示例如表1所示.

表1　评价模型的一般性示例

评价者的评价行为使得他们彼此相互联系起来，而不再是孤立的评价者个体，这一思想是建立网络模型的着眼点. 为了更清楚地说明这一问题，以表1为例，可以发现评价者1和评价者2因为共同评价了商品1和商品2而联系起来. 由于评价者的偏好和评分不同，这些评价者之间就存在着“合作”和“冲突”的关系，这一关系是建立网络博弈模型的着眼点. 注意到如果两个评价者给出的评价较为一致，他们在网络中表现出了更多的“合作”关系；如果两个评价者给出的评价差别较大，则他们表现出了更多的“冲突”关系；而这些关系恰恰是网络博弈，分析纳什均衡的基础，通过接下来的效用分析，可以发现该博弈均衡的结果决定着网络中各个评价者的权重分配(也可以理解为“影响力”).

为了刻画评价者之间合作和冲突的关系，以及量化这一关系，定义评价者之间的关系强度矩阵为σ=[σij]i,j=1,…,n，其中σij表示评价者i和评价者j之间的关系量化值.

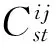
由此，综合两位评价者对全部商品的评价信息，得到

(1)

关于该定义性质和合理性的讨论：

性质1当两位评价者(记为i和j)评价了全部的既有商品，并给出一致的评价偏好时，σij=1；如果给出完全相反的评价，则σij=-1.

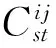
性质1给出了关系强度矩阵的两个极端值，反映了完全一致和完全不一致的情况；由此还可以推得-1≤σij≤1.

性质2当两位评价者评价的商品交集为空集时，σij=0.

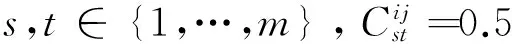
证毕.

注意到，性质2意味着在构建的网络中，如果评价者之间没有共同的评价商品，他们之间没有联系，是彼此孤立的.

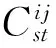
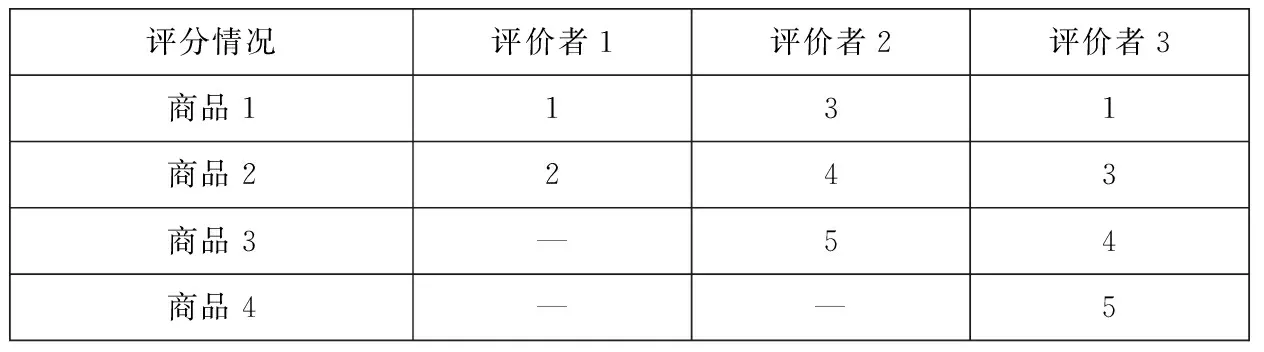
表2　关系强度矩阵适用于刻画缺失数据的示例

根据以上的定义，可以算得σ12=1/6和σ23=1/2. 从表中给出的信息，可以发现三位评价者在评价了的商品上是有着一致偏好的，但因为评价者1有着更多未评价的信息，其和评价者2之间的关系强度就小于评价者2和评价者3之间的关系强度，注意到评价者3给出了全部四种商品的评价. 由于未评价的商品难以判断偏好，所以以上的结果是合理的. 如果定义的关系强度指标只考察评价了的商品，不考虑未评价的商品，则评价者1和评价者2之间的关系强度是1，同理，评价者2和评价者3之间的关系强度也是1，这显然不如本文考虑未评价商品，给出一个折中的分数0.5来的合理. 这是本文的定义能够处理未评价商品(也即存在缺失数据)合理性的体现.

在以上着眼点和关系矩阵定义的基础上，由评价行为构成的网络模型是明确的：评价者{1,…,n}构成了网络中的点，由评价信息得到的评价者之间的关系矩阵σ=[σij]i,j=1,…,n构成了网络的边及其权重，特别当权重为0时，意味着边是不存在的. 根据关系矩阵的定义及性质，可以发现该关系矩阵反映了评价者之间“合作”和“冲突”关系的大小及强弱. 由此，当给定每个评价者的效用函数时，该网络博弈问题就是明确给定的.

本文给出如下的评价者效用函数

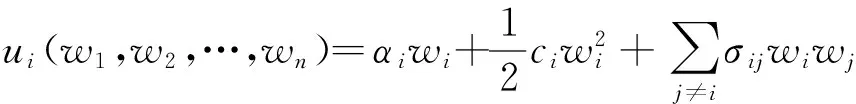
(2)

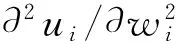
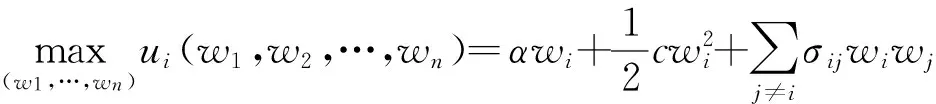
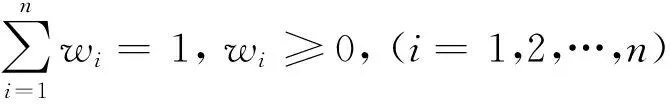
(3)

从形式上看，这个最优化问题并不复杂；但是从博弈的观点看，其是多个主体参与的静态博弈问题，其中博弈的参与人是网络中的评价者(或称为节点)，参与人的收益是他们的目标函数并彼此相互影响(注意到本文中每个参与人都有一个目标函数)，参与人的行动集是他们各自的权重，而博弈的信息则是全体的参与人都相互了解彼此给出的评价，这体现在效用函数的关系矩阵里. 那么该最优化问题的解是不是唯一的Nash均衡点，或者在参数满足怎样的条件下，其为唯一的Nash均衡点？该问题的解与网络中节点中心性的刻画指标是否有着内在的关联，其还将联系着关于网络结构怎样的特征指标？以及所获得的权重对于得到的最终评价结果将有怎样的有益效果？本文将在第2和第3部分逐一解答这些问题. 但首先，对模型的假设做一个评述，这也成为进一步分析模型合理性和适用范围的基础.

1.2关于模型假设的评述

在1.1节中，指出了模型基于的假设为“每位评价者是理性的评价者，其认真对待自己做出的评价，并期望该评价被广泛接受，最大化地发挥其评价的价值”. 事实上，这个假设一定程度上也给出了模型的适用范围；注意到，经常可以发现有一类在线的评价者专门故意给出虚假的打分信息，用以抬高对其有利商品的评分，打击与其竞争商品的评分. 事实上，这一类评价者也符合以上的假设，其目的就是他的评价被广泛接受，这类评价者属于理性评价者的范畴. 但是，有些评价者是不严肃的，他们对自己和他人的评价持无所谓的态度，这类评价者不属于理性评价者的范畴，其不符合该模型讨论的范围，如果所分析的数据中，有大量这类非理性的评价者，该文的模型不适用. 不过对于现实生活中，事实上有大量非理性评价者的评价集并不多见，因为绝大多数人对于在线评价，或者自己所从事的评价领域的工作还是有其目的性和严谨性的，所以，本文的模型事实上适用的范围是广泛的.

2　模型的解及相关性质

2.1等价变换与模型求解

为了便于分析该网络博弈均衡的情况，并探索最优解与网络中心性测度的联系，首先对式(3)最优化问题的目标函数ui(w1,w2,…,wn)中的参数做一个等价变换，如下

(4)

这里的σij即为“定义1”中给出的评价者之间的关系强度矩阵σ=[σij]i,j=1,…,n中的元素，则上式中的γ,λ以及gij(i≠j)都是明确的，可以从σij算出；进一步令矩阵δ=[δij]i,j=1,…,n，其中δii=c和δij=σij(i≠j)，则以上的变换写成矩阵形式为

δ=-β·I-γ·U+λ·G

(5)

其中I是n阶的单位矩阵，U是矩阵元素全为1的n×n的矩阵，同时G=[gij]i,j=1,…,n. 注意到令u=(u1,u2,…,un)T和w=(w1,w2,…,wn)T，则目标函数的矩阵形式为

u=α·w+δ·w=α·w+

(-β·I-γ·U+λ·G)·w

(6)

从式(5)和式(6)可以发现，事实上等价变换的结果是将原始的矩阵拆分为了几个部分. 在求解这个模型前，关注矩阵G的性质和网络Bonacich中心性的定义，其对于进一步分析解的性质是导论性的基础.

性质4矩阵G中的元素满足gii=0，且当i≠j时，0≤gij≤1，并且其为对称矩阵.

证明由式(4)和式(5)易见，矩阵δ的对角线元素都为c，其来源于式(5)等号右边的前两项，因此可以算得gii=0，也即矩阵G对矩阵δ的对角线没有贡献；由γ和λ的定义，可见γ≥0，并且λ≥σij+γ≥0，因此根据式(4)的第二个子式有0≤gij≤1. 再则由式(4)中σij=-γ+λgij,(i≠j)的关系，由于矩阵σ是对称的，则矩阵G也为对称的.

矩阵G的这个性质使得其满足了邻接矩阵的基本条件，是定义Bonacich中心性的基础，这一点将在本文的2.3节进一步讨论.

定义2(网络中Bonacich中心性的定义[21])给定一个网络g和它的邻接矩阵G=[gij]，要求gii=0，并且当i≠j时，0≤gij≤1；给定递减参数φ，使得I-φG是可逆并且正定的，则网络节点的Bonacich中心性构成的列向量b(g,φ)=[I-φG]-1·1，其中1是组成元素全为1的列向量.

该网络中心性的定义最早由Bonacich提出，是比较常用的中心性测度指标，曾被用于许多讨论网络节点重要性的应用中，一个较好的综述可以参见Guimerà等的文献[22].

引入Langrange乘子l，将式(4)的关系和式(6)代入约束最优化问题式(3)中，可以得到如下定理1所示的结果.

定理1已知评价者之间的关系强度矩阵σ=[σij]i,j=1,…,n，如果选定合适的β参数值使得I-(λ/β)·G可逆并且正定，则式(3)最优化问题的解为

(7)

其中bi(g,λ/β)是列向量b(g,λ/β)的第i个元素，b(g,λ/β)是“定义2”给出的以λ/β为递减参数的Bonacich中心性列向量. 这时，Langrange乘子l为

(8)

证明由Langrange乘子法，设定Langrange乘子为l，则最优化问题(3)的一阶条件为(α+l)·1+δ·w=0，其中0是组成元素全为0的列向量，将式(5)代入有

(α+l)·1+(-β·I-γ·U+λ·G)·w=0

(9)

也即

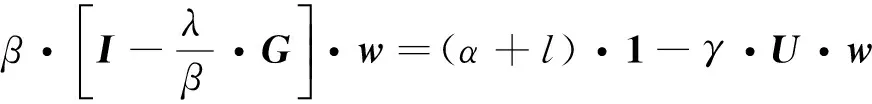
根据Bonacich中心性的定义(也即定义2)，有

(10)

同时注意到，目标函数关于w是上凸的，所以以上的解为满足极大值的最优解，再由I-(λ/β)·G可逆并且正定的条件，所有节点的网络节点的Bonacich中心性是非负的，也即所有的wi非负，其满足式(3)约束条件的第二个部分，由此以上定理1得证.

定理1给出了最优化问题(3)解的形式，如果这个解是存在的，那么由定理1所示的求解过程，可见其恰恰是该网络博弈问题的Nash内点均衡解(最优解不在边际上，并且由求导得到的最优解满足Nash均衡解的定义)；但就参数β的值如何选取才能保证以上的解存在，以及以上的最优解是不是Nash均衡的唯一解等问题未做讨论，这将在2.2节中进一步分析. 但从以上结果可以发现：每个评价者最优的权重分配就是他们各自归一化了的Bonacich中心性，这个中心性与参数β有关，因为λ可从评价者关系强度矩阵中算出，事实上反观式(4)，这个参数β是由效用函数中反映边际效用递减规律的参数c决定的；而参数α并不影响最优权重值的分配，因为在式(7)中没有出现这个反映边际收益的参数α，因此其对于决定Nash内点均衡的存在性和唯一性也是不重要的，在计算权重分配时，这个参数是可以不给定的，这是从解的形式得到的分析结果.

2.2Nash内点均衡解的存在性及唯一性

通过以上的定理1，这里Nash内点均衡存在性的问题就归结为参数β值的选择问题，要求合理选定该值其使得I-(λ/β)·G可逆并且正定. 该值的选定范围由定理2给出.

定理2(Nash均衡内点解的存在性定理)矩阵I-(λ/β)·G可逆并且正定，当且仅当β>λμ1(G)，其中μ1(G)是矩阵G的最大特征根.

证明根据Debreu和Herstein的定理[23]，矩阵I-a·G可逆并且正定的充要条件是0≤a<1/μ1(G)，这时有[I-a·G]-1=I+a·G+a2·G2+…. 这类似于一元函数(1-a·x)-1可展开的条件为a<1/|x|. 由此，将λ/β视为Debreu和Herstein的定理中的a，结合式(4)，β和λ都非负的事实，有定理2成立.

在定理2的基础上，结合评价者之间的关系强度矩阵σ的相关性质(定义1及3个相关性质)，则有以下的推论成立，其表述了参数β取值范围的一个普适性的安全区域，是一个充分条件.

推论1(参数β取值范围的充分条件)当β>2·(n-1)时，对于任意的关系强度矩阵σ，都有矩阵I-(λ/β)·G是可逆并且正定的，也即由定理1得到的解是式(3)所示问题的Nash内点均衡解.

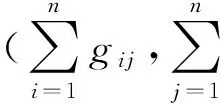
在推论1的基础上，事实上得到了对于任意强度矩阵σ都安全的β值下界的取值范围，比如：该下界可取为2·n-1(注意到其只与评价者人数n有关，与他们之间的关系强度矩阵无关)，此时，该网络博弈问题的Nash均衡内点解必然存在.

以下证明由定理1得到的内点解是该问题的唯一Nash均衡解，这由定理3给出.

定理3(内点解是唯一的Nash均衡解)在满足Nash均衡内点解存在性的前提下，由定理1得到的最优解是该问题唯一的Nash均衡解.

证明只需考察是否存在边界解满足Nash均衡条件，因为在内点的范围内，以上的内点解是唯一的最优解，由于从定理1的求解过程中可以发现其是唯一的最优解.

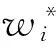
于是，由于最优解在边界达到，对于i∈S中的那些评价者，其一阶导数满足：∂ui/∂wi(w*)≤0，具体求解该一阶导数得到

(11)

而对于j∈N-S的那些评价者，由于其在内点，一阶导数满足：∂uj/∂wj(w*)=0，即

(12)

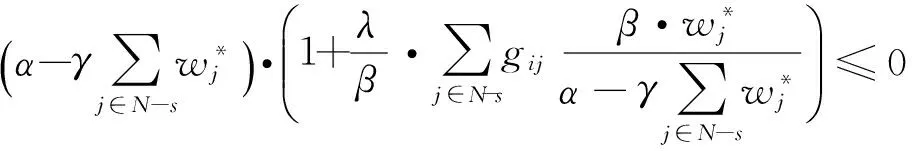
结合式(12)即为

(13)

由定理2和定理3可知通过定理1求得的最优解是这个网络博弈问题的Nash均衡内点解，并且这个解是这个问题唯一的Nash均衡解.

2.3解与网络中心性测度的关系

在定理1的求解中建立了最优解与网络Bonacich中心性测度的关系，同时定理2给出了参数β的取值范围，本节将深入分析这一问题，关注于β→+∞和β→λμ1(G)这两个极端值的情况，注意到后者是定理2给出的β取值的合法下界，这由两个性质给出：

性质5当β→+∞时，网络中所有评价者有着一致的权重，即为简单平均的情形.

证明由定义2，可见

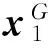
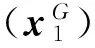
证明根据本文的性质4，由于矩阵G是对称矩阵，其满足以下的分解关系

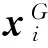
当β→λμ1(G)时，可知：1-λβ·μ1(G)→0，从而上式两边取极限得到

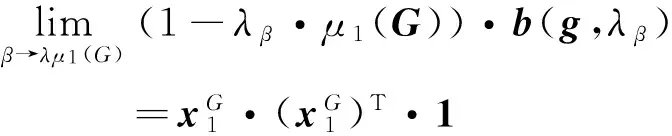
于是，对于b(g,λβ)组成元素的有限和，成立

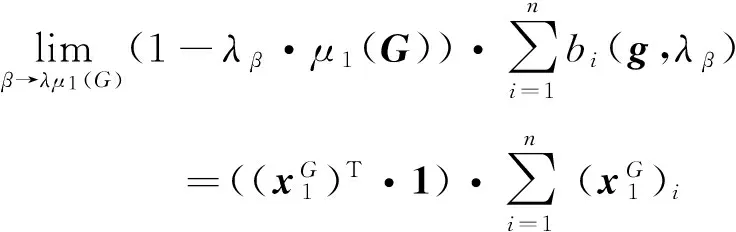
将上式代入式(7)，有

性质5和性质6给出了β取值极端的情形：其中一个收敛到了评价者权重相等，即简单平均的情况；另一个收敛到了归一化的主特征向量，而后者恰恰也是网络节点中心度的定义，称为主特征中心度. 由此可见，简单平均和主特征中心度都是本文得到的最优权重的极端情况，这是理论统一性的一个体现.

3　算例、仿真分析及模型的应用

3.1优良评价结果的两个特征及一个算例

从以上的方法中可以发现，模型中只有一个参数是需要给定的，用以决定评价者的权重，这个参数为β. 那么该参数决定了评价结果的哪些性质呢？为此，首先考虑一个优良的评价结果应该有怎样的特征，在本文中归纳了两个特征如下：

特征1(保序性及保序性指标)一个优良的评价结果应该能够最大程度地反映既有评价者的评价序关系(也即：基于评价结果的全部商品的排序应该与既有的更多的评价者的排序是一致的)，通常该指标由Kendall’sTau(简记为Tau)给出，其定义可以参见Hochbaum的文献[24]附录. 注意到评价结果的Tau值越大，说明其保序性越好.

特征2(稳定性及稳定性指标)任何数据集都包含不可避免的噪声干扰，这些噪声可能来自于评价者本身的评价失误，也可能来自数据收集的过程，也可能是人为特意加入的，比如为了提高自家商品的评分而不断人为地引入虚假的好评. 当数据集存在这些问题时，一个好的评价方法得到的评价结果应该是稳定的，也即受这些数据的干扰小. 为此，令其基于未加入干扰的数据集(记为dataor)的评价结果为ror，加入干扰数据的评价结果为rfa，则稳定性指标Rob定义为

Rob=-|Tau(dataor,ror)-Tau(dataor,rfa)|

(14)

其中m为全部商品的数量，Tau为“特征1”中定义的保序性指标. 显然，以上Rob的值越大越稳定，说明加入干扰后，针对原有数据集的保序性指标变化较小，这是结果稳定性的体现.

为了具体说明以上的两个特征，给出算例如下：

表3　说明评价结果两个特征的算例

由表3可见：在基于真实评价的保序性分析上，当β=5时，得到的最终评价结果对于商品m2和m3的排序与原有评价者n2和n4是不同的，但是当β=1时，得到的最终评价结果与原有评价信息对于三种商品的排序完全一致，这也证实了“特征1”指标的有效性；再者，在考虑加入干扰时的稳定性时，可以发现当β=5时，排序与原有没有加入干扰时是一致的，但当β=1时，这个排序发生了变化，由此可见“特征2”的指标是合适的.

相对于既有的权重方法，在理论上，本文的方法完全从评价者给出的评价分数出发，没有引入主观的不确定因素，这不同于AHP方法或ANP方法[25]需要引入专家打分的体制，并且相对于“引言”中列举的其他方法而言，本文的方法有一个调控参数β，该参数的引入使得本文的方法更加灵活，可以处理含有虚假数据的情形，并能合理控制解的“保序性”，而这一点是其他的既有方法不能做到的；不仅如此，本文的方法可以处理缺失数据存在的情形，不需要引入差值、预估等手段填补缺失数据，使得结果更加客观，遵从于原始的信息. 在实践上，注意到作为本文方法特例的“简单平均方法”常作为一个基准用以比较评价方法的好坏[24]，本文中基于表3给出的算例，应用“简单平均值方法”的结果如表4所示.

对比表4和表3中的结果，可以发现“简单平均方法”相比于β=1的结果，保序性很差，其与评价者n4的评价偏好不完全一样，并且“简单平均方法”没有调控参数，使得能够处理的数据集非常单一. 根据2.3节的论述，“简单平均方法”的结果与β取较大值时的结果比较接近，这时将会导致评价结果的满意度大打折扣. 通过以上算例和对比分析，证实了本文方法的可行性，同时也发现随着参数β取不同的值，解的“保序性”和“稳定性”特征会发生变化，以下在3.2节通过仿真分析探索这个变化的规律.

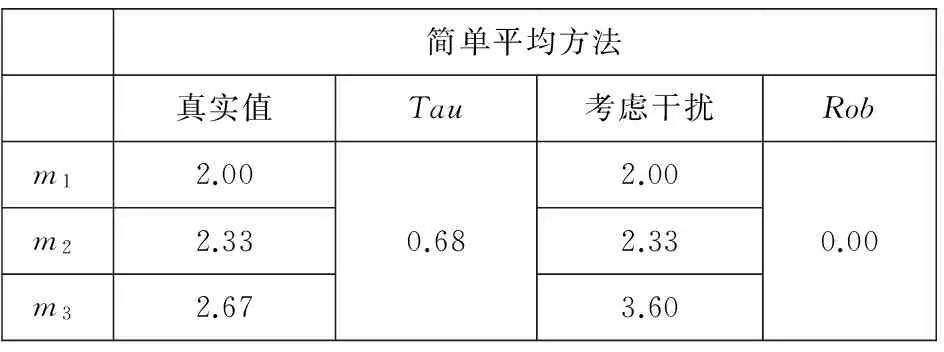
表4　简单平均方法的结果

这一部分集中分析当参数值β变化时，解的两个优良属性变化的情况. 不失一般性，设定商品数m为20，评价者人数n为30，采用5分评价体制，1分最差，5分最好. 首先随机生成评价者对商品的打分信息，注意到在现实生活中，绝大多数情况下评价者不会对全部的商品都进行评价，而只是对其中的一部分进行评价，特别是对于在线购物，商品数目繁多，每个评价者不可能购买全部的商品并都进行评价，这里设定评价概率为p，令p从0.4变到1，步长为0.1，考察3.1节中“特征1”给出的保序性指标的值，如表5所示. 注意到表中每个值是基于该点参数仿真100次取平均的结果，这是为了消除个别随机数据带来的严重偏差，获得一个较为稳健的结果.

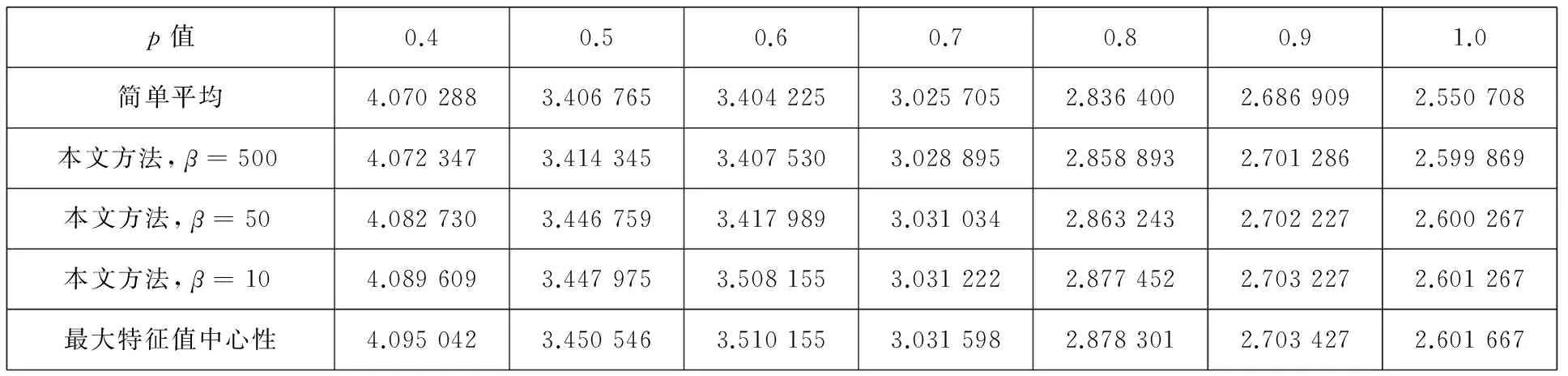
表5　不同的p值条件下各种方法的保序性指标值

注：为了便于比较和结果较为清晰，表中的数据为原始数据变换的结果，其公式如下：-ln(-x)，其中x是原始数据，该变换保持了单调性，同时使得结果便于纵向比较.

从表5可以发现：随着β值的变小，评价结果的保序性变好，并且“简单平均方法”和“最大特征值中心性方法”是两个极端情形，简单平均方法有着最差的保序性，而最大特征值中心性方法有着最好的保序性，当β值较大时，其结果接近简单平均方法，当β值较小时，其结果接近最大特征值中心性方法，这点也与2.3节的理论分析相一致.

类似于表3所示的算例，这里认为原始生成的m为20，n为30，固定评价概率p为0.6的数据集是真实的评价，设定虚假评价者n′，从1到15，其对于标号为1的商品评5分，标号为2的商品评1分，成为这样一个制造虚假数据的评价者集合. 由于原始的数据是随机生成的，所以指定商品1和2有着一般性，同样每个点是基于100次仿真取平均的结果，考察不同的β值对于结果稳定性(由3.1节“特征2”给出)的影响，如图1所示. 该图表明随着β值的增加，评价结果的稳定性变好；其中，简单平均方法有着最好的稳定性.

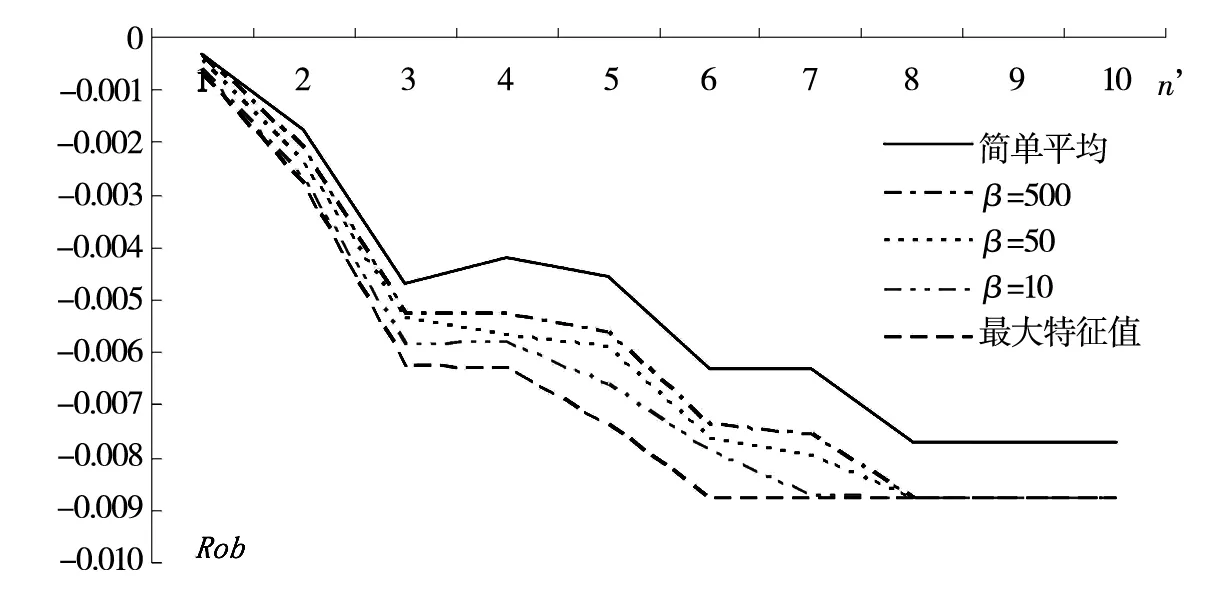
图1不同数量的虚假评价者情形下各种方法的稳定性指标值

基于以上仿真结果的发现：随着β值的增加，评价结果的保序性变差，但评价结果的稳定性变好. 这个结论说明了β值的选择是矛盾统一体，如果这个值选的过小，虽然在保序的方面结果是良好的，但是在稳定性方面结果就变的较差，而这个值选的过大，则恰恰相反. 这一点提示要根据数据的特征去选定β值，如果数据本身的质量不够好，里面包含的噪声干扰和虚假数据比较多，这时可以考虑β值取的大一点，用以获取比较稳定的结果，而如果数据质量较好，则β值可以取的小一点，这时“保序性”是问题的主要矛盾. 由此，可以得到以下启示性的结果：β值的选取影响优良数据的两个特征，两个特征随着β值的变化是此消彼长的关系，因此要根据数据集本身的特点选定合适的β值，如果数据质量较差，则选择稍大的β值，如果数据质量较好，则选择较小的β值.

3.3模型在“在线电影评价”中的应用

将本文的模型应用于在线电影评价的数据集，该数据集是一个开放的二手数据集，其描述了不同的客户对于不同电影的打分情况，该数据集的网址为www.grouplens.org. 该数据集包含了100 000条评分数据，反映了943位客户对于1 682部电影的打分情况，评分从1分到5分不等，1分最差，5分最好. 将本文的方法直接应用于该数据集，并与简单平均和主特征值中心度方法的结果进行对照，如表6所示. 该表的结果证实了仿真分析中的结论，在“主特征值中心度方法”下，得到了最优的“保序性”指标，但是如果该数据集中有潜在的虚假数据，则兼顾“稳定性”和“保序性”的评价结果应该选择一个合适的β值，如果认为该数据质量较好，则选择较小的β值，比如β=200；如果认为该数据质量不好，则选择较大的β值，比如β=2 000. 同时该应用分析也证实了方法在实践中的可行性.

表6　在实际数据集基础上的方法对比分析结果表

4　结束语

在评价理论与方法的研究中，如何确定评价者或决策者的权重是一个重要的问题，因为其影响着最终的评价结果，也影响着结果的客观属性. 本文考虑了评价者们通过评价行为建立起来的联系，在网络科学中，这也被称为“网络交互影响效应”. 本文建立了一个网络博弈的模型，将评价者视为点，评价行为视为边，边的权重由评价者评价分数的一致性给出，其体现了评价者之间“合作”和“冲突”的关系；由此，在给出效用函数的基础上，确定了该博弈问题的最优化模型；并就模型的假设和模型的适用范围进行了讨论.

本文基于分解的技巧和Lagrange乘子方法给出了模型的最优解，并给出了参数的取值范围，证明了参数在适当的取值范围内，模型的最优解是Nash均衡的内点解，并且是这个问题的唯一Nash均衡解；不仅如此，本文建立了最优解和网络中心性测度的联系，指出了该问题的最优解与归一化的Bonacich中心性是一致的，并揭示了解的两个极限值分别为基于简单平均方法获得的评价值和基于主特征值中心度方法获得的评价值，解释了这些方法的内在关联，将简单平均方法和主特征值中心度方法统一到本文的理论框架中.

本文进一步提出了一个优良的评价解应满足的两个特性：保序性和稳定性，前者反映评价结果与既有评价者偏好的一致性，后者反映当存在干扰数据时，评价结果的鲁棒性. 通过算例和仿真分析，探索了模型参数不同的取值对两个特性的影响规律，发现“随着参数β值的变化，两个特性是此消彼长的关系，当β值增加时，评价结果的保序性变差，但评价结果的稳定性变好”这一规律，由此建议根据数据集本身的特点选定合适的β值，如果数据质量较差，则选择稍大的β值，如果数据质量较好，则选择较小的β值，这一相机抉择的策略有助于在结果的两个特性中获得一个较好的折中. 本文的方法同样应用于一个在线电影评价的真实数据集，体现了模型的实用性.

就管理实践来说，本模型可以直接应用在在线商品的综合评价中，给出能够反映既有评价信息的较为综合的评价结果，完善电子商务中在线商品的排序与评价；也可以应用于项目的评审过程，给出评审者合理的权重分配，得到一个使得全体评审者满意度较高的综合结果；还可以应用于选举过程，学科评估，期刊评价等等领域. 不仅如此，由于模型中进入了参与者的社会网络，这使得网络分析的技术可以进一步应用在模型中，这构成了模型的衍生应用. 比如：可以利用网络社团划分的技术，求出各个社团个性化的评价值，解释集团利益的存在与差异，其对于组织管理具有实践意义；也可以利用网络分析中相似节点的挖掘技术，甄别虚假评价，剔除这类有色噪声的干扰，使得评价结果更趋合理. 这些都成为扩展模型进一步的工作. 综上所述，本文提出的模型是一个确定评价者或决策者权重分配的新方法，具有理论意义和实践意义.

[1]Xu Z S, Yager R R. Power-geometric operators and their use in group decision making[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(1): 94-105.

[2]Fan Z P, Yue Q, Feng B, et al. An approach to group decision-making with uncertain preference ordinals[J]. Computers & Industrial Engineering, 2010, 58(1): 51-57.

[3]Gordy M B, Willemann S. Constant proportion debt obligations: A postmortem analysis of rating models[J]. Management Science, 2012, 58(3): 476-492.

[4]郭亚军, 侯芳. 面向评价局部环境的导向性群组评价方法研究[J]. 管理科学学报, 2013, 16(2): 12-21.

Guo Yajun, Hou Fang. Oriented group evaluation method for partial evaluation environment[J]. Jorunal of Management Sciences in China, 2013, 16(2): 12-21. (in Chinese)

[5]宋马林, 吴杰, 曹秀芬. 环境效率评价方法的统计属性分析及其实例[J]. 管理科学学报, 2013, 16(7): 45-54.

Song Malin, Wu Jie, Cao Xiufen. Analysis of statistical properties of environmental efficiency evaluation and its illustrations[J]. Jorunal of Management Sciences in China, 2013, 16(7): 45-54. (in Chinese)

[6]李永立, 吴冲. 基于图模型和最优化的评价方法[J]. 系统工程学报, 2013, 28(6): 403-409.

Li Yongli, Wu Chong. Inventing an evaluation method based on graph model and optimization[J]. Journal of Systems Engineering, 2013, 28(6): 403-409. (in Chinese)

[7]French J R P. A formal theory of social power[J]. Psychological Review, 1956, 63(3): 181.

[8]Bodily S E. A delegation process for combining individual utility functions[J]. Management Science, 1979, 25(10): 1035-1041.

[9]Mirkin B, Fishburn P. Group Choice[M]. Washington: Winston, 1979.

[10]Brock H W. The problem of “utility weights” in group preference aggregation[J]. Operations Research, 1980, 28(1): 176-187.

[11]Ramanathan R, Ganesh L S. Group preference aggregation methods employed in AHP: An evaluation and an intrinsic process for deriving members’ weightages[J]. European Journal of Operational Research, 1994, 79(2): 249-265.

[12]宋光兴, 邹平. 多属性群决策中决策者权重的确定方法[J]. 系统工程, 2001, 19(4): 84-89.

Song Guangxing, Zou Ping. The method of determining the weight of the decision-maker in multi-attribute group decision-making[J]. Systems Engineering, 2001, 19(4): 84-89. (in Chinese)

[13]Van den Honert R C. Decisional power in group decision making: A note on the allocation of group members’weights in the multiplicative AHP and SMART[J]. Group Decision and Negotiation, 2001, 10(3): 275-286.

[14]徐泽水, 达庆利. 多属性决策的组合赋权方法研究[J]. 中国管理科学, 2002, 10(2): 84-87.

Xu Zeshui, Da Qingli. Study on method of combination weighting[J]. Chinese Journal of Management Science, 2002, 10(2): 84-87. (in Chinese)

[15]Xu Z S. Group decision making based on multiple types of linguistic preference relations[J]. Information Sciences, 2008, 178(2): 452-467.

[16]Yue Z. A method for group decision-making based on determining weights of decision makers using TOPSIS[J]. Applied Mathematical Modelling, 2011, 35(4): 1926-1936.

[17]Yue Z, Jia Y. An application of soft computing technique in group decision making under interval-valued intuitionistic fuzzy environment[J]. Applied Soft Computing, 2013, 13(5): 2490-2503.

[18]Candogan O, Bimpikis K, Ozdaglar A. Optimal pricing in networks with externalities[J]. Operations Research, 2012, 60(4): 883-905.

[19]Vives X. Strategic supply function competition with private information[J]. Econometrica, 2011, 79(6): 1919-1966.

[20]Lu Y, Musalem A, Olivares M, et al. Measuring the effect of queues on customer purchases[J]. Management Science, 2013, 59(8): 1743-1763.

[21]Bonacich P. Power and centrality: A family of measures[J]. American Journal of Sociology, 1987, 92(5): 1170-1182.

[22]Guimerà R, Diaz-Guilera A, Vega-Redondo F, et al. Optimal network topologies for local search with congestion[J]. Physical Review Letters, 2002, 89(24): 248701.

[23]Debreu G, Herstein I N. Nonnegative square matrices[J]. Econometrica, 1953, 21(4): 597-607.

[24]Hochbaum D S, Centeno E M, Yelland P, et al. Rating customers according to their promptness to adopt new products[J]. Operations Research, 2011, 59(10): 1171-1183.

[25]Saaty T L. The modern science of multicriteria decision making and its practical applications: The AHP/ANP approach[J]. Operations Research, 2013, 61(5): 1101-1118.

An evaluator’s weight allocation considering network peer effects

LIYong-li1,WUChong2,ZHANGXiao-fei2

1. School of Business Administration, Northeastern University, Shenyang 110169, China;2. School of Management, Harbin University of Technology, Harbin 150001, China

Determining the weights of evaluators is an important step in evaluation methods. This paper proposes a new method to determine an evaluator’s weight based on network game， and detailed discussions and validations of the solution and parameters are given. This paper considers evaluators as network nodes, and the evaluations as the links between the evaluators, which make up the edges of the network. Based on the evaluators’ rating information, this paper defines the “Cooperation” and “Confliction” matrix between the evaluators as the weight matrix of the network. A network game model is established and the optimal solution is solved as the weight values. It is proved that the optimal solution is a Nash interior equilibrium solution and the only Nash equilibrium solution of this problem. Furthermore, this paper analyzes the relationship between the optimal solution and network-centricity measure, and the meaning of optimal solution in network science; namely, this paper linkes up the knowledge of decision-making theory and network science. Through mathematical proofs and simulation analyses, this paper reveals the meaning of the parameters in the model, which determine two excellent properties of the solution: “isotonicity” and “stability”. Accordingly, this paper proposes an approach on parameter selection based on the features of the data set, and applies the model in a real data set. In conclusion, the weight allocation method is practical, and it could balance the two good properties of the solutions.

evaluation theory and method; optimization model; network analysis; peer effect; network game; weight allocation; simulation

① 2013-11-11；

2013-12-31.

国家自然科学基金资助项目(71501034); 辽宁省社会科学基金资助项目(L15CGL014).

李永立(1985—)， 男， 辽宁沈阳人， 副教授， 硕士生导师. Email: ylli@mail.neu.edu.cn

F724.6

A

1007-9807(2016)04-0032-13