基于空间Panel data分位数回归的粮食产量分析

赵佩佩，袁永生，吴楠楠

(河海大学 理学院，江苏 南京 211100)



基于空间Panel data分位数回归的粮食产量分析

赵佩佩，袁永生，吴楠楠

(河海大学 理学院，江苏 南京 211100)

在对空间面板数据和分位数回归基本原理进行全面分析说明的基础上，选用全国31个省市2000～2012年的面板数据，对其进行了平稳性检验，考察了粮食生产的空间相关性，利用分位数回归方法对影响我国粮食产量的各影响因素进行了实证分析，根据估计结果定量分析了我国粮食产量的主要影响因素及其影响程度。研究结果表明：各省粮食生产存在空间相关性，而且粮食播种面积、农用化肥使用量和农业劳动力对粮食产量有重要影响，农用机械动力和受灾面积对粮食产量影响在不同分位点处表现不一，受灾面积则是粮食产量的抑制因素。

面板数据；空间相关性；分位数回归；粮食产量

0　引言

中国作为农业大国，粮食生产问题受到社会各界的广泛关注，进入2000年以来，由于种种原因，我国粮食产量连续4年持续下滑，整体进入一个徘徊、下降的变动周期，库存连续下降，到2003年，粮食产量减少为4.31亿t，粮食供不应求，创1990年以来粮食产量的最低点，2004年以后，粮食产量才逐步回升。同时，由于各地区之间的各生产要素投入不同，粮食生产在不同省份之间也表现出不同程度的差异。因此，为促进我国粮食产量稳定增长，对粮食生产的空间相关性及影响因素这一历史性课题进行探究具有重要的现实意义和历史意义。

近年来，粮食安全问题备受关注，国内外学者对此展开了激烈的讨论，Iddo Kan等(2006)对格鲁吉亚农业发展现状进行了研究，发现耕地面积和质量能提高农场产出[1]；伍山林等(2000)利用全国截面数据对中国粮食生产主要因素进行了研究，认为土地与农业劳动力对粮食生产有重要影响[2]；胡冰川(2006)等运用面板数据的固定效应模型对江苏省粮食生产的投入产出影响因素进行了分析，发现耕地投入和农资投入对粮食生产有积极作用[3]。马文杰等(2008)用面板数据模型对全国粮食生产1999～2004的投入产出数据进行了分析，认为粮食播种面积是影响目前中国粮食生产的最主要因素，农业机械总动力、劳动力和农用化肥使用量对粮食产量仍旧具有正的效应[4]；朱再清等对湖北省粮食产量采用OLS法建立回归模型，并对不同时期的粮食生产投入与产出的弹性进行了比较分析[5]，在引入空间面板数据后，胡亚全利用空间模型对气候变化、农业生产条件进行了实证分析[6]。

综观现有研究发现，目前关于粮食产量影响因素的定量研究相对欠缺，所选用的数据多为横截面数据或者时间序列数据，所用方法多依赖于普通OLS回归，且多为均值模型，只描述了因变量条件均值的变化，没有全面地描述因变量在不同分位数下条件分布的全貌，使得大量的信息被忽略了，而且很少考查变量在空间上的相关性。针对现有研究的不足，本文选用2000～2012年我国31个省区粮食产量的面板数据，利用空间面板数据和分位数回归的方法研究我国各省区粮食生产的空间相关性及粮食产量的影响因素，考察不同分位点上各影响因素对粮食产量的影响，并与普通OLS回归进行对比，得到各分位点的回归系数，更好地描述了各影响因素在不同分位点上与粮食产量的关系，更加细致地描述了对粮食产量的影响程度。

1　相关理论及研究方法

1.1空间面板数据

面板数据是由大量个体的时序观测构成的数据集，与单纯的时序数据集和横截面数据集相比，面板数据具有更多优势，它的自由度更高，能够有效降低解释变量之间的共线性程度和观测个体之间的变异性，而且，面板数据还融合了个体之间的差异性和内在动态变化，为变量间的不可观测效应研究提供了依据。由于地域差异和时间变化的存在，个体在空间维度上的相互作用越来越明显，即面板数据具有空间相关性，这使得通过对截距项的差异设置来更多地强调空间个体的差异性的传统面板数据模型不再适用，基于此，空间面板数据模型着重描述空间状态下的相关性，弥补了传统面板数据模型的不足[7]。

空间面板数据是在普通面板数据模型的基础上考虑了空间相关性和空间异质性，其模型结合了空间计量经济学方法和面板数据的优点，能够同时描述时间和空间上的变化规律，比单独考虑时间变化的时间序列数据和仅考虑地域差异的截面数据具有更广泛的适用性，已经在经济学、地理学、农学和管理学等领域得到了广泛应用。由于空间面板数据具有空间相关性,是非独立的，因此在使用空间面板数据模型时加入空间权重矩阵，以此来反映空间相关性。另外，在使用空间面板数据模型研究问题时，还要对模型的个体效应进行判定：固定效应与随机效应哪个更合适[8]。一般而言，用样本数据推断总体效应时选用随机效应回归模型，直接对样本数据进行分析时采用固定效应模型。

1.2全局空间相关性理论

基于空间面板数据理论，为综合分析我国粮食产量的空间效应，首先要对个体变量进行空间相关性分析。检验全局空间自相关的指标和方法很多，本文选用的是Moran’s I指数。Moran’s I不易受偏离正态分布的影响，能够更好地反映空间相邻区域单元属性值的相似程度，应用较为广泛。根据Morm的定义，Moran’s I指数表达式为[9]：

(1)

(2)

(3)

(4)

1.3分位数回归

分位数回归理论上是对以古典条件均值模型为基础的最小二乘法的扩展，是一种更一般化的估计方法，在传统的回归模型中，普通最小二乘法比较常用，它的基本思想是估计给定解释变量的条件下被解释变量的条件均值，阐述了解释变量对被解释变量的均值影响，而分位数回归是根据被解释变量的条件分位数对解释变量进行回归，得到所有分位数下的回归模型，它能更精确地描述解释变量对被解释变量的变化范围以及条件分布形状的非对称影响，描述分布的尾部特征。

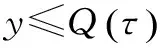
面板线性回归模型如下：

Yit=αi+Xitβ+uit

(5)

Y的τ分位数为：

(6)

τ分位数回归的目标函数为：

(7)

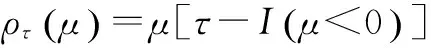
(8)

为示性函数。求使得函数F(β;τ)极小的一阶条件为：

(9)

分位数回归的基本思想是：首先赋予其回归线上方点的权重为τ，回归线下方点的权重为1-τ，然后求误差绝对值的加权和。关于τ取值的含义，根据解析几何原理，它表示回归线或回归平面表面或以下的数据占全体数据的百分比，举例说明，若τ=0.9，则1-τ=0.1，线性规划得到的0.9的条件分位数表明数据的90%分布在模型所形成的回归线或平面的表面或表面以下，10%分布在回归线或表面以上，这说明分位数回归是在因变量的条件分布的不同分位点上量化自变量的技术[12]。

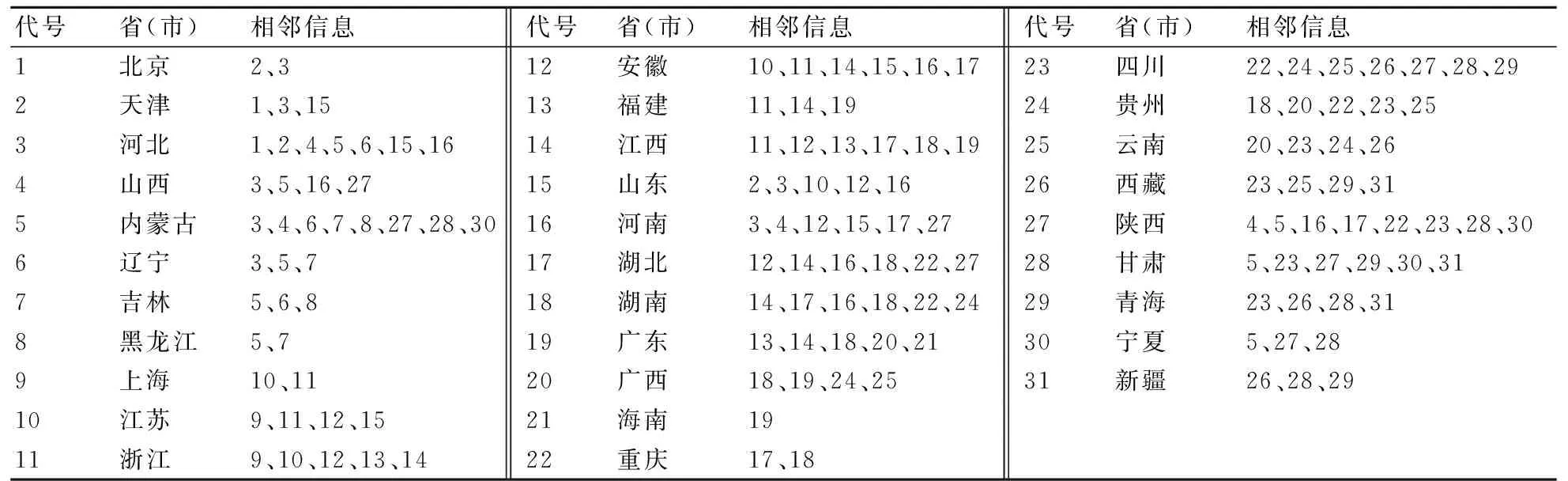
表1　中国31个省(市)自治区相邻信息

注:资料源自《中华人民共和国地图》。由于海南省与其他省没有共同陆地边界，故以距离它最近的广东省作为它的相邻区域。

2　实证研究

2.1模型的设定

经过对现有文献的总结分析及客观上经验数据的制约，模型设定以面板数据和空间作用论为理论基础，选定粮食产量的影响因素为粮食播种面积、农用化肥使用量、机械动力、农业劳动力、有效灌溉面积和受灾面积。选用的数据为2000～2012年31个省区粮食生产的面板数据，数据来源于国家统计局《中国统计年鉴》和各省统计年鉴。

分析投入与产出关系常用的是柯布—道格拉斯生产函数(C—D函数)，它对变量取对数不仅可以做到无量纲化，减少异方差，而且还有明确的经济意义。由于本文模型变量间是投入产出关系，故采用柯布—道格拉斯生产函数来确定模型形式。

设定面板数据模型为：

i=1,…,31,t=1,…,13

(10)

其中，Y为粮食总产量(万t)，S为粮食播种面积(千hm2)，H为农用化肥使用量(万kg)，K为机械动力(万kW·h)，L为农业劳动力(万人)，G为有效灌溉面积(千hm2)，Z为受灾面积(千hm2)。

2.2面板数据单位根检验及协整检验

为避免由于面板数据不平稳性所造成的模型伪回归，因此在进行建模前，首先要对数据的平稳性进行检验，检验序列平稳性常用的基本方法是单位根检验，它也是构建模型的基础性检验。由检验结果可知，原始序列的对数序列不全为平稳序列，而一阶差分序列均为平稳序列(表2)，说明原始序列的对数序列均为I(1)，即一阶单整，在满足同阶单整的条件下对粮食产量与其影响因素进行协整检验(表3)，检验结果表明：粮食产量与各影响因素之间存在协整关系。

2.3模型形式检验

在对面板数据模型进行回归分析之前，一般要先确定模型形式，本文通过F检验区分混合回归模型、变系数模型和变截距模型，以此来确定模型形式，再根据Hausman检验来确定模型是随机效应还是固定效应。对本文所设面板数据模型形式的检验步骤如下：

首先进行F检验，假设模型为变系数模型yit=αi+βixit+uit时，得残差平方和为S1=2.319；假设模型为变截距模型yit=αi+βxit+uit时，得残差平方和S2=5.013；假设模型为混合回归模型yit=α+βxit+uit时，得残差平方和为S3=9.616。本文所选样本数据中N=31，T=13，K=6，由此计算得出统计量为：

模型设定对应的原假设为H3:αi=αj,βi=βj，当原假设成立时F3～F(210,186)，给定显著性水平分别为0.05和0.1时，查表得临界值F0.05(210,186)=1.27，F0.1(210,186)=1.20，F3>临界值，故拒绝原假设H3；进行假设H2的检验，原假设为H2:αi≠αj,βi=βj，当原假设成立时，F2～F(180,186)，给定显著性水平分别为0.05和0.1时，查表得F0.05(180,186)=1.28，F0.1(180,186)=1.21，F2<临界值，所以接受原假设H2，认为模型为变截距模型：yit=αi+βxit+uit。故本文根据检验结果选择变截距模型。

再对所设面板数据模型进行Hausman检验，检验结果显示在5%显著性水平下拒绝随机效应模型，应建立固定效应模型，检验结果符合直接对样本数据进行分析时采用固定效应模型的一般用法，故本文模型为固定效应模型。

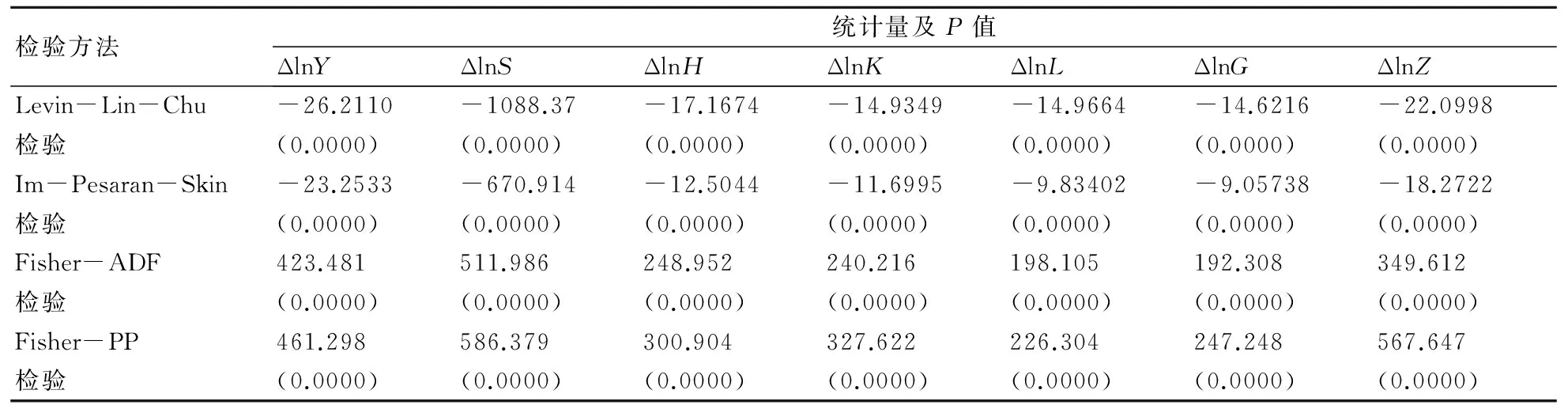
表2　单位根检验结果

注:括号内为检验的概率P值。下同。

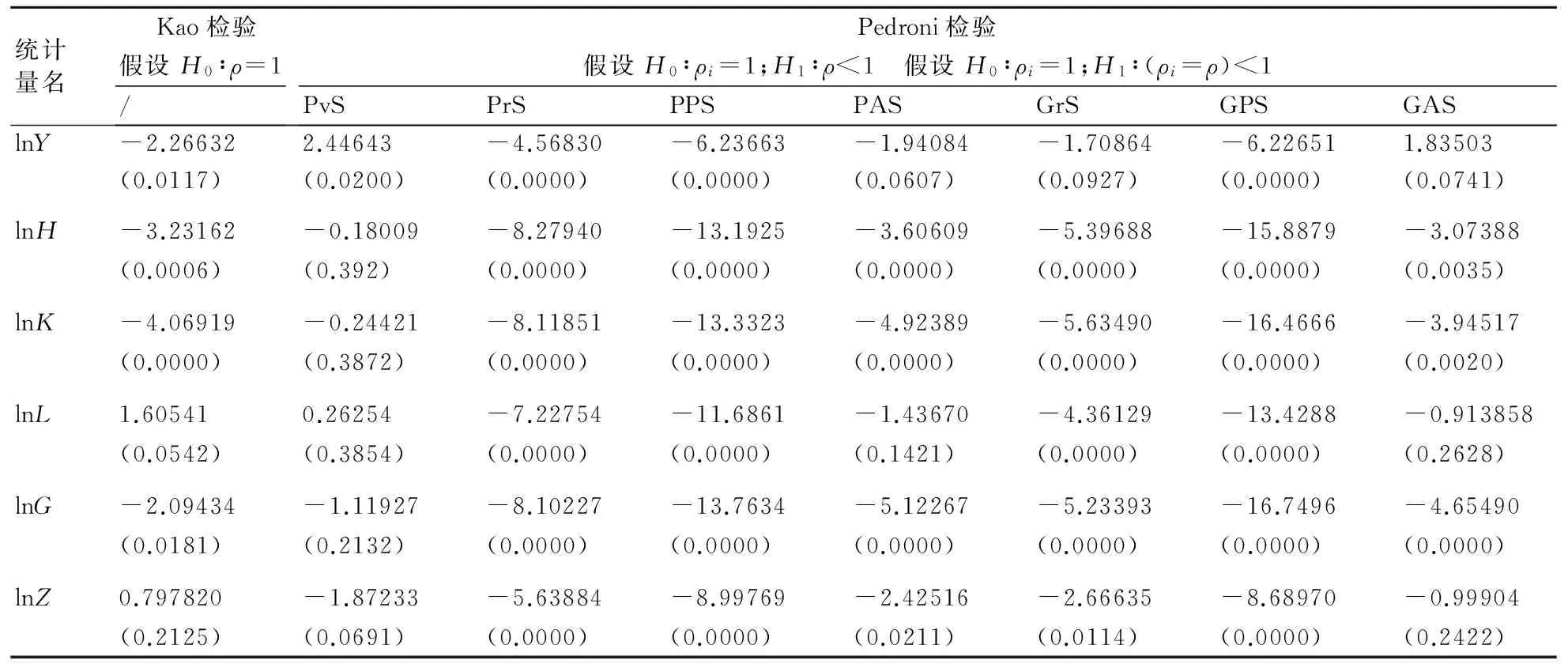
表3　协整检验结果(P值)

2.4空间相关性检验

在研究空间数据时，若忽略空间相关性的存在，则会得出极不精确的结果。因此，在研究过程中，对空间相关性的检验尤为重要。先对粮食产量进行探索性空间分析，据上述空间相关性计算方法，运用Matlab软件得到我国31个省(市)自治区在2000～2012年间粮食产量的Moran’sI指数值和Z值，结果见表4。

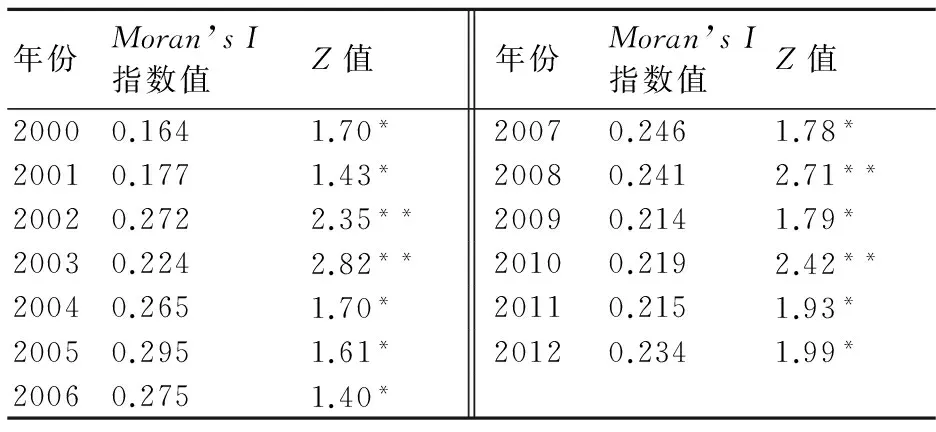
表4　中国粮食产量Moran’s I指数值

注:*表示在5%水平下显著，**表示在1%水平下显著。

从表4中统计值可以发现，我国省级粮食产量具有显著的正的空间相关性，这说明我国各省区粮食产量的空间分布不是相互独立变化的，某省区的粮食生产会影响到相邻省区的粮食生产。这主要是由于相邻省区之间的劳动、资本相互流通，农业经济关联性比较强，使得相邻省区之间的粮食产量呈现空间相互影响，因此在研究省级粮食生产影响因素分析的模型中需要引入空间分析。

2.5分位数回归

在检验空间相关性的基础上，为了详细说明各影响因素对粮食产量的影响，进一步描述它们之间的关系，本文利用空间面板数据，采用变截距固定效应模型，通过分位数回归方法进一步研究了在不同分位点条件下各影响因素对粮食产量的影响，检验结果见表5。

表5　分位数回归结果

根据回归分析结果，相比OLS回归，面板分位数回归对各因素的影响关系更加具体，结论如下：

2.5.1粮食播种面积对粮食产量有正面影响在OLS回归和分位数回归中可以发现：粮食播种面积所对应的系数估计量β1几乎均为正数，表明粮食播种面积对粮食产量的影响较大，有显著的促进作用，符合生产实际。但随着经济的快速发展和工业化、城市化进程的加快，我国耕地面积还在继续减少，耕地资源的数量和质量也在下降，如果强行大量增加生产发达省份的粮食播种面积，并不利于粮食产量的增加和经济的发展。基于此，在高分位点0.9出现系数估计量负的情况，说明在农业发达的省份再加大粮食播种面积反而降低农业总产值。

2.5.2化肥使用量对粮食产量有正面影响在OLS回归和分位数回归中化肥使用量的系数估计量β2均为正，说明不论是农业发达省份还是不发达省份，化肥使用量的增加都促进了粮食产量的增加，但是化肥使用量的系数在低分位点高于高分位点，这说明化肥使用量对农业不发达省份的影响大于农业发达的省份，因此，农业不发达省份需要大量使用化肥来增加粮食产量，而农业相对发达省份，其化肥使用量已相对较为充足，再加大化肥投入所带来的产粮食产量增长空间有限。

2.5.3机械动力对粮食产量有影响从表5中可以看出：机械动力的系数估计量β3在0.1分位点处为正，其余分位点均为负，农用机械动力对粮食产量在较低分位点处能够促进粮食产量的增加，在中高分位点处呈下降趋势，起反作用。表明对于农业发展处于较低水平的省份，农业机械化投入的增加会增加粮食产量，促进农业发展，系数估计量的下降趋势说明并不是机械化程度越高越好，目前我国多数地区粮食生产仍处于小田作业，农民通常以传统生产技术为主，现代农业科技在粮食生产中应用较少，尤其是科技含量较高的农用机械，因此当农业机械化程度到达一定水平后，再加大投入科技含量较高的农用机械，只会造成机械过剩，增加成本，反而降低了农业总产值。

2.5.4农业劳动力对粮食产量有正面影响从表5的OLS回归和分位数回归中可以发现：农业劳动力对粮食产量影响较大，但是农业劳动力对粮食产量的影响在第一个分位点0.1为负，其余均为正，而且绝对值都较大，这表明劳动力投入对粮食生产有积极影响。从理论角度而言，农业劳动力系数在正常情况下不可能为负，即使在劳动力极其过剩的状况下，农民理性种植经验决定了不可能出现在种植过程中由于投入人力较多而导致粮食产量下降的情况，而且在农业较发达的省份，农业发展前景好，引进专业人才对农业发展有极大的促进作用，但是对农业发展比较落后的省份，农业劳动力投入的增加不会对农业发展起积极作用，反而会因为生产条件差、粮食消耗多而导致粮食生产相对下降。

2.5.5有效灌溉面积对粮食产量有影响在OLS回归中，有效灌溉面积系数估计量为正，说明有效灌溉面积的增加对粮食发展有积极作用，但在分位数回归中，有效灌溉面积系数估计量两头负中间正，这说明了对于农业中等发展的省份，有效灌溉面积的增加有利于粮食生产，但对于农业较发达的省份和较不发达的省份，有效灌溉面积的增加对粮食生产起反作用，这也许不符合生产理论，但是可以解释为对于农业较发达的省份，有效灌溉面积已经得到较充分的利用，对于较不发达的省份，有效灌溉面积有限，所以粮食生产可增幅的空间受限。

2.5.6受灾面积对粮食产量有负面影响受灾面积在OLS回归中和各个分位点系数均为负，统计结果十分明显，受灾面积的增加引发粮食产量的下降。

3　结论与建议

本文利用空间面板数据和分位数回归模型对我国31个省份2000～2012年粮食生产的数据进行建模分析，根据模型检验结果可知，本文所选数据为一阶单整序列，粮食产量与各影响因素之间存在协整关系，采用变截距固定效应模型，空间相关性检验结果表明我国各省区粮食生产存在空间正相关性，因此在研究省级粮食生产影响因素分析的模型中需要引入空间分析。相比普通OLS回归模型，面板分位数回归模型更精确地描述了各影响因素在不同分位水平对我国粮食产量的影响程度，分析结果表明粮食播种面积、农用化肥使用量和农业劳动力对粮食产量有重要影响，农用机械动力和受灾面积对粮食产量影响在不同分位点处表现不一，受灾面积则是粮食产量的抑制因素。

根据本文实证研究结果，针对性的给出以下政策建议。

(1)政府应该制定更加合理有效的农业政策，加强对粮食生产的调控力度，合理引导和利用粮食生产的空间差异，建立空间分布合理的粮食生产体系，稳健调整粮食产区，完善农业生产体系。

(2)采取有效措施稳定粮食播种面积，保证粮食生产安全，合理引导剩余劳动力，避免农业劳动力的大量流失，确保农业生产所需的劳动力。随着工业化、城市化进程的加快，如果农村劳动力大量流失和耕地面积被强行占用，将对粮食生产产生较大的负面影响，因此，应制定严格的耕地保护制度，稳定粮食播种面积；完善农业补贴政策，合理引导农业劳动力。

(3)合理施用化肥，根据粮食生产状况，适度、适量、适时的科学施肥，提高粮食单位产量，保证粮食生产安全。过量滥用化肥会造成土壤板结，导致土壤有机结构恶化，影响耕地质量，造成农业生态环境的破坏，严重影响我国环境友好型农业的可持续发展。针对当前现状，我国应推行广施农家肥、测土配方施肥、精准施肥等可持续发展技术。

(4)根据农业生产现状，研发并投入符合当前生产力水平的机械动力，培养从事农业技术推广的专业人才，大力发展农机社会化服务，增加农业机械的实用性和不同区域的适用性。同时改善农田灌溉条件和技术，保证粮食增产的有效灌溉面积，并完善配套政策体系，让科技进步真实高效地服务和促进我国粮食生产。

[1] Iddo K, Kimhi A, Lerman Z. Farm output, non-farm income and commercialization in rural Georgia [J]. Journal of Agricultural and Development Economics, 2006, 3(2): 276-286.

[2] 伍山林.中国粮食生产区域特征与成因研究[J].经济研究，2000(10)：38-45.

[3] 胡冰川，吴强，周曙东.粮食生产的投入产出影响因素分析：基于江苏省粮食生产的 实证研究[J].长江流域资源与环境，2006(1)：71-75.

[4] 马文杰，冯中朝.中国粮食生产影响因素分析——基于面板数据的实证研究[J].陕西农业科学，2008，54(1)：163-166.

[5] 朱再清，陈昉源.湖北省粮食生产模型与投入要素效益比较分析[J].湖北农业科学，2006，45(5)：531-533.

[6] 胡亚权.空间面板数据模型及其应用[D].武汉：华中科技大学，2012：82-90.

[7] Hsion C. Analysis of Panel Data(2nd ed)[M]. United Kingdom, Cambridge：Cambridge University Press, 2003.

[8] 谢识予，朱弘鑫.高级计量经济学[M].上海：复旦大学出版社，2005.

[9] 陆文聪，梅燕.中国粮食生产区域格局变化及其成因实证分析——基于空间计量经济学模型[J].中国农业大学学报，2007，24(3)：140-152.

[10] 马荣华，蒲英霞，马晓冬.GIS空间关联模式发现[M].北京：科学出版社，2007.

[11] 李群峰.基于分位数回归的面板数据模型估计方法[J].统计与决策，2011(17)：24-26.

[12] 吴建南，马伟.估计极端行为模型：分位数回归方法及其实现与应用[J].数理统计与管理，2006，25(5)：536-543.

[13] 罗万纯，陈永福.中国粮食生产区域格局及影响因素研究[J].农业技术经济，2005 (6)：58-64.

[14] 梁子谦,李小军.影响中国粮食生产的因子分析[J].农业经济问题，2006(11)：19-23.

[15] 刘贤赵，张安定，李嘉竹.地理学数学方法[M].北京：科学出版社，2009.

[16] 高铁梅.计量经济分析方法与建模：EViews应用实例(第二版)[M].北京：清华大学出版社，2006.

(责任编辑：管珊红)

Analysis of Grain Yield Based on Spatial Panel Data and Quantile Regression Model

ZHAO Pei-pei, YUAN Yong-sheng, WU Nan-nan

(College of Science, Hohai University, Nanjing 211100, China)

Based on the spatial panel data and the fundamental principles of quantile regression analysis, the panel data were collected from 31 provinces (cities) in China during 2000～2012, and the spatial correlation of grain crop production was examined by stationarity test. The influencing factors of China’s grain yield were analyzed by quantile regression, and the main influencing factors and their impacts on China’s grain yield were quantitatively analyzed according to the estimated results. The results of the experiments showed that the spatial correlation of grain crop production existed in different provinces, and the sown area of grain crops, chemical fertilizer application rate, and agricultural labor force had important influences on grain yield. However, the effects of agricultural machinery power and damage area on grain yield were various in different quantiles. Comprehensively, the damage area was considered to be the inhibiting factor of grain yield in China.

Panel data; Spatial correlation; Quantile regression; Grain yield

2016-03-04

江苏省水利科技创新基金项目(2011059)；河海大学自然科学基金资助项目(2009426311)。

赵佩佩(1988—)，女，江苏徐州人，硕士研究生，研究方向：面板数据。

F326;O212

A

1001-8581(2016)08-0115-06