Simulation and Experimental Investigation of Thickness Measurement Using Pulsed Eddy Current Technique*

YANG Panpan，CAO Binghua，FAN Mengbao，XIE Wei（.School of Mechatronic Engineering，China University of Mining and Technology，Xuzhou Jiangsu 226，China；2.School of Information and Electrical Engineering，China University of Mining and Technology，Xuzhou Jiangsu 226，China）



Simulation and Experimental Investigation of Thickness Measurement Using Pulsed Eddy Current Technique*

YANG Panpan1，CAO Binghua2*，FAN Mengbao1，XIE Wei1
（1.School of Mechatronic Engineering，China University of Mining and Technology，Xuzhou Jiangsu 221116，China；2.School of Information and Electrical Engineering，China University of Mining and Technology，Xuzhou Jiangsu 221116，China）

A 2D finite-element model is established for thickness measurement using pulsed eddy current（PEC）technique due to axisymmetric of transient magnetic field.The PEC differential signals were calculated using the de⁃veloped theoretical model for sheets with different conductivity and thickness.Through analysis on PEC signals due to samples，the peak amplitudes are considered as the desirable signal features for thickness evaluation.The simula⁃tion results show that the peak value of the PEC differential signal increases when the sheet under test becomes thicker.The metal sheet with higher conductivity also makes the peak value of PEC differential signal larger as well. The observations from the experimental measurements agree well with those from simulation data，which validates the developed model and the simulated results.

nondestructive testing；thickness measurement；pulsed eddy current；finite elementsimulation；peak value

各类轧制金属板材是现代机械制造过程中的重要材料，而金属板材厚度是质量控制与状态监测过程中的重要参数。因此对金属板材厚度进行检测是非常必要的［1-4］。超声法［5］要求被测表面光洁且需要耦合剂；射线法［6-7］的放射源会伤害操作人员的身体健康，因此实践操作中需要严格防护，且防护设备成本很高。基于电磁感应原理的常规涡流法［8-9］采用单频或多频正弦信号激励，受趋肤效应影响，渗透能力有限，信息量相对较少。

与常规涡流法相比，脉冲涡流法采用周期性脉冲信号激励，具有丰富的频谱内容，在金属材料厚度及缺陷检测方面得到了广泛应用［10-12］。Tai C C［13］采用基于查表法的快速反演方法同时测量了金属基体上镀层的厚度和电导率。Shin Y K［14］通过提取差分信号峰值时间和过零时间作为信号特征对金属板的厚度和电导率进行评价。Suresh K［15］采用悬臂梁末端的永久磁铁与非磁性导电薄板产生混合磁场影响系统谐振频率的方法对非铁磁性导电薄板进行厚度检测。Zhang Jianhai［16］采用脉冲涡流差动探头通过提取差分信号峰值和峰值时间作为信号特征对铁磁性钢管上金属防腐涂层进行厚度检测。然而，前述研究中未考虑电导率和厚度同时变化对信号特征的影响。

在当前的研究基础上，本文建立了脉冲涡流厚度检测的有限元理论模型，仿真研究了金属材料厚度和电导率对探头差分信号的影响，搭建了脉冲涡流厚度检测系统并对仿真结果进行验证。

1　有限元建模与仿真

脉冲涡流检测是基于电磁感应原理的无损检测方法。当探头靠近被测金属板材时，被测板材中感应电流产生的涡流场会改变空间磁场，从而引起探头中感应线圈的电压发生变化。

本文的脉冲涡流探头采用了圆柱型线圈，被测板材无缺陷且各向同性，因此，空间电磁场具有轴对称特性。据此，可将模型由3D转化为2D。利用有限元仿真软件COMSOL multiphysics建立了脉冲涡流2D轴对称模型进行仿真，如图1所示。探头是由激励线圈和检测线圈组成，右侧虚线表示求解区域边界，左侧虚线表示对称轴。

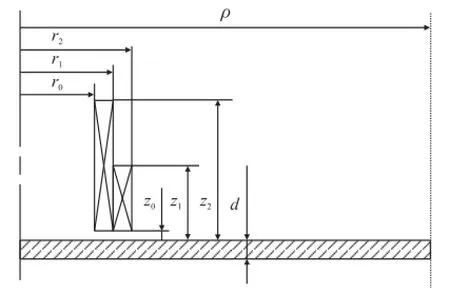
图1　脉冲涡流2D轴对称模型

激励线圈内径r0为5 mm，激励线圈外径（检测线圈内径）r1为6 mm，检测线圈外径r2为7 mm，探头的提离距离z0为0.3 mm，激励线圈高度（z1-z0）为10 mm，检测线圈高度（z2-z0）为4 mm。设置激励线圈匝数为200匝，检测线圈匝数为1 000匝，求解域半径ρ设置为100 mm。被测板材厚度d以0.1 mm为增幅，从0.1 mm递增至1 mm。激励信号选择频率为100 Hz、幅值为10 V、时间常数为0.1 ms的方波信号。理论上，脉冲激励信号的上升沿与下降沿产生的感应信号大小相同、方向相反，因此本文只展示了方波激励信号的前半个周期及其对应的响应信号，方波激励信号的前半周期波形如图2所示。

设置被测板材的电导率参数为37 MS/m，相对磁导率为1，厚度范围为0.1 mm～1.0 mm。对各个厚度进行仿真，得到探头输出信号。为便于提取厚度信号特征值，在信号处理过程中以无试件时探头输出信号为参考信号，将被测板材在不同厚度时得到的探头输出信号与之做差，得到差分信号，如图3所示。

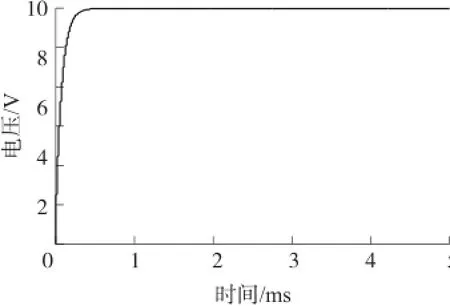
图2　激励信号

图3　差分探头仿真信号

由图3可知，差分信号峰值随着被测板厚度变化有明显的变化，厚度值越小对应的差分信号峰值越小，厚度越大对应的差分信号峰值就越大。提取各差分信号峰值作为厚度变化的信号特征，得到差分信号峰值与被测板材厚度参数之间的关系曲线，如图4所示。

图4　不同厚度试件的仿真信号峰值变化

由图4可知，被测板材厚度参数与差分信号峰值之间存在一一对应的关系。对于电导率为37 MS/m、厚度范围为0.1 mm～1.0 mm的被测板材，随着厚度的增大，差分信号峰值也是逐渐增大的；曲线斜率随着厚度的增加而逐渐减小，说明差分信号峰值对厚度变化的灵敏度随厚度的增加而逐渐减小。因此，实际检测中，为了提高检测的灵敏度，应尽量保证待测板材厚度位于高灵敏区。

实践中，金属材料种类繁多，其电导率也不同。根据脉冲涡流检测原理，当材料电导率发生变化时，探头差分信号峰值也会发生变化。因此，需要研究电导率变化对探头差分信号峰值的影响。设置电导率参数范围为13 MS/m～59 MS/m，相对磁导率为1，厚度为0.5 mm。仿真计算各试件的探头差分信号，并提取各差分信号峰值作为信号特征，得到差分信号峰值与电导率之间的关系曲线，如图5所示。

图5　不同电导率试件的仿真信号峰值变化

由图5可知，随着被测板材电导率的增加，差分信号峰值以线性方式逐渐变大，这表明脉冲涡流可用于电导率检测，且对于0.5 mm厚的板材，电导率与差分信号呈线性关系。目前，电导率检测一般采取常规涡流法，且要求待测板材厚度须大于3倍渗透深度。当应用常规涡流检测薄板材的电导率时，为了保证检测要求，通常需要提高检测频率，如从60 kHz提高到120 kHz、480 kHz或更高，或者将多层板材叠加以增加厚度。频率提高后涡流效应影响更明显，而多层叠加导致各层之间出现空隙，这均会降低检测精度。因此，采取差分信号峰值作为信号特征，脉冲涡流可用于检测薄板材的电导率。

为了研究电导率和厚度同时变化对差分信号峰值的影响，设置仿真参数：电导率范围为13 MS/ m～59 MS/m，相对磁导率均为1，厚度范围为0.1 mm～1.0 mm。仿真计算各试件的探头差分信号，并提取差分信号峰值，结果如图6所示。

对图6进行分析发现，当电导率和厚度增加时，信号峰值也变大，因此厚度检测时要求待测试件的电导率分布要均匀，否则电导率的分布差异会给厚度检测引入较大误差。在相同的频率下，电导率低的板材厚度检测灵敏度低于电导率高的板材厚度检测灵敏度。电导率高的材料，其量程比低电导率的材料的量程小。这表明，当应用脉冲涡流法测量不同材料的厚度时，需要根据电导率的变化调整检测频率。为了提高厚度检测灵敏度，需要增大检测频率，而要增加检测量程，则需要减小检测频率。另外，由于电导率和厚度之间存在一一对应关系，通过制作合适的标准试件，运用脉冲涡流差分信号峰值可同时测量材料的厚度和电导率。

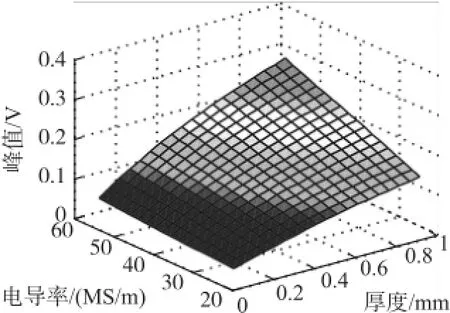
图6　不同电导率、不同厚度的仿真信号峰值变化

2　实验研究

为了验证有限元模型及仿真结果的正确性，搭建了脉冲涡流厚度检测系统进行实验研究，如图7所示。信号采集卡选择16位模拟输入/输出、单通道最大采样率1.25 MS/s的USBX-6356。功率放大器选择固定增益为10倍、全功率带宽为1 MHz的LPA05B。试验中的激励信号频率为100 Hz，占空比为50%，幅值为0.5 V。激励信号经功率放大器放大10倍后幅值由0.5 V变为5 V。将放大后激励信号接入脉冲涡流探头。探头的输出信号经信号调理电路和信号采集卡后输入上位机。信号采集卡的采样频率设置为1 MHz。

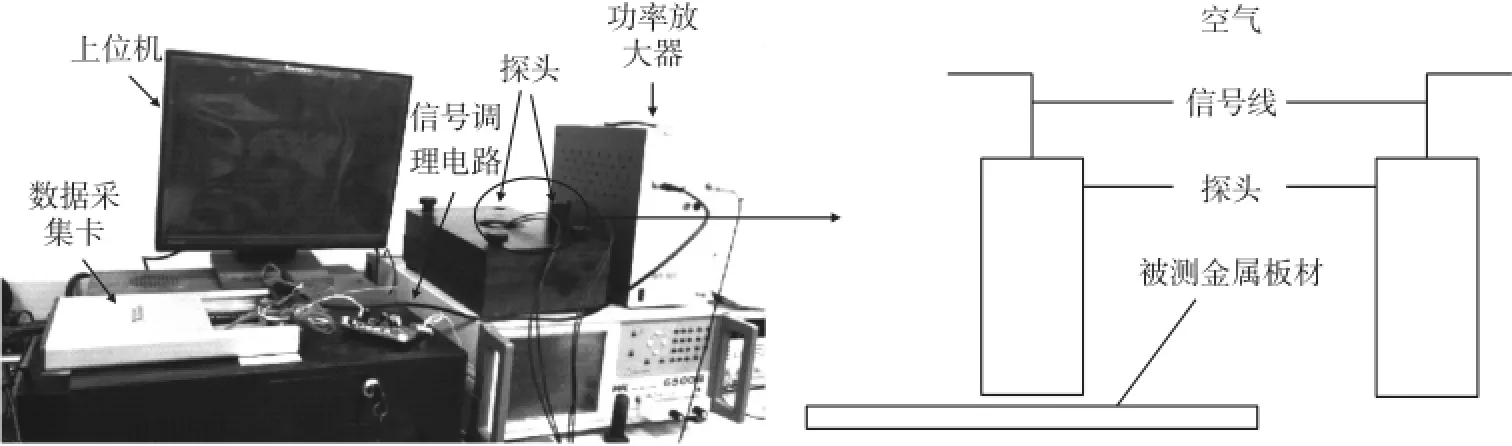
图7　脉冲涡流厚度检测系统示意图

由于被测板材厚度较小，自然状态下存在轻微的弯曲变形，在试验过程中对多层板材进行检测时易导致各层板材之间存在空气间隙，从而导致实验结果产生偏差。为解决这一问题，实验系统采用了专用夹具对被测板材进行夹紧。实验系统使用了差分脉冲涡流探头［17］，一个探头置于被测金属板材正上方，另一个探头则置于空气中用作产生差分参考信号。未经滤波的差分探头信号，如图8所示。

图8　未滤波的差分探头信号

从图8可以看出，未滤波的差分探头信号存在较多的毛刺噪声。为提高信号质量，本实验系统对未滤波的差分探头信号利用移动平均滤波器进行滤波处理。移动平均滤波器的计算公式如下：

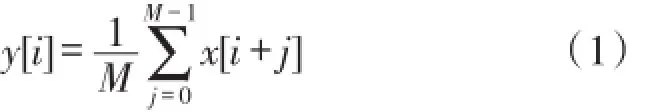
其中，x［］为输入信号，y［］为输出信号，M为移动平均滤波器的窗宽。

若移动平均滤波器窗宽M过小则不能有效的去除随机噪声，移动平均滤波器窗宽M过大则会降低信号幅值，影响信号质量。综合考虑以上因素，通过多次尝试，最终指定移动平均滤波器窗宽M为15。对未滤波的差分探头信号进行滤波处理后分别得到黄铜、铝合金和紫铜（黄铜电导率约为14.29 MS/m、铝合金37.74 MS/m、紫铜55.56 MS/m，相对磁导率均为1）三种材料的差分信号，如图9～图11所示。

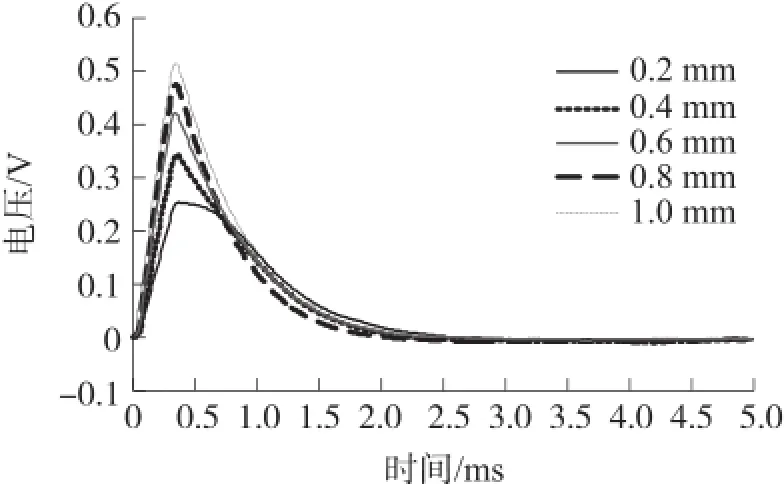
图9　黄铜的实验差分信号

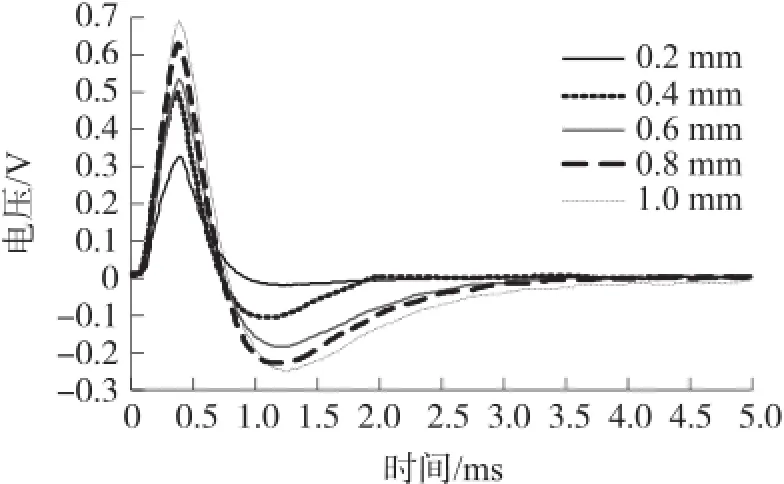
图10　铝合金的实验差分信号

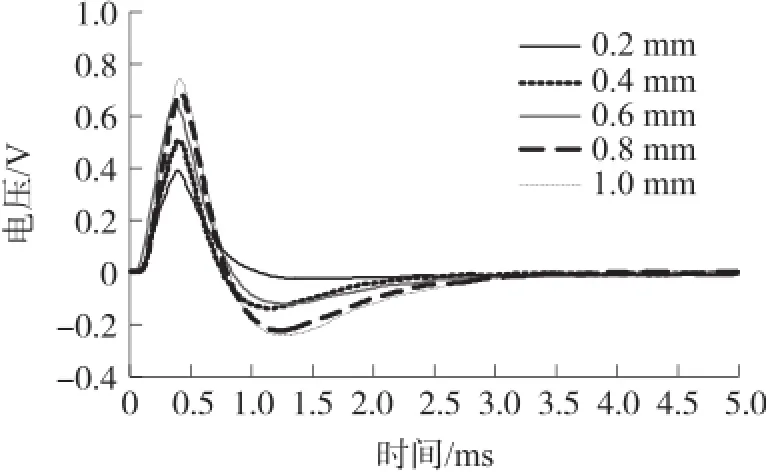
图11　紫铜的实验差分信号

由图9～图11可知，对于黄铜、铝合金和紫铜三种材料，差分信号峰值随着被测板厚度变化均有明显的变化，厚度越小对应的差分信号峰值越小，厚度越大对应的差分信号峰值越大。通过提取各差分信号峰值作为信号特征，分析差分信号峰值与被测板材厚度、电导率之间的关系，如图12所示。

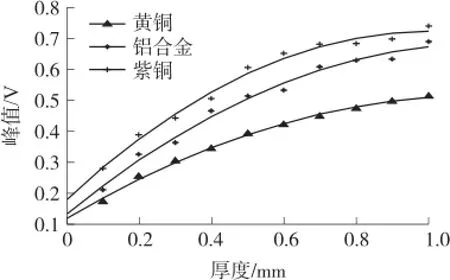
图12　不同材料试件的实验信号峰值变化

由图12可知，被测板材的厚度范围为0.1 mm～1.0 mm时，随着被测板材厚度的增加，差分信号峰值增加；而相同厚度的板材，紫铜的差分信号峰值比铝合金和黄铜的信号峰值大，这表明电导率增加会引起信号峰值变大。在厚度较小阶段，紫铜板材对应的信号峰值变化最快，铝合金次之，黄铜最小，说明检测厚度较小的板材时，紫铜板材的灵敏度最高，而黄铜的最低。上述实验结论与仿真结论一致，表明，本文所建立的有限元模型是正确的，而且根据模型仿真得到的结论是可信的。然而，由于实验系统信号的重复性稍差、板材厚度和电导率不均匀等原因，实验得到的差分信号峰值存在波动现象。

3　结论

本文利用有限元方法建立了脉冲涡流厚度检测响应信号的理论模型。仿真研究了厚度和电导率变化对探头差分信号峰值的影响规律，结果表明，当板材厚度和电导率增加时，信号峰值增加，因此要求待测试件的电导率必须一致，否则待测试件的电导率差异会给厚度检测引入误差；电导率大的材料，其厚度检测灵敏度大，检测量程小，相应地，电导率低的材料，其厚度的检测灵敏度小，但检测量程大。最后，搭建了脉冲涡流厚度检测系统，并对紫铜、铝合金和黄铜三种材料的厚度变化进行了实验研究。数据分析发现，实验结果与仿真结果一致，验证了所建理论模型的正确性与仿真结果的可信性。

下一步，拟改进试验系统信号质量，根据本文研究结果优化厚度系参数以提高脉冲涡流厚度检测精度。

［1］Yin W，Peyton A J.Thickness Measurement of Non-Magnetic Plates Using Multi-Frequency Eddy Current Sensors［J］.NDT& E International，2007，40（1）：43-48.

［2］Qu Zilian，Zhao Qian，Meng Yonggang.Improvement of Sensitivi⁃ty of Eddy Current Sensors for Nano-Scale Thickness Measure⁃ment of Cu Films［J］.NDT&E International，2014，61（1）：53-57.

［3］Fan Mengbao，Cao Binghua，Yang Panpan et al.Elimination of Lift⁃off Effect Using a Model-Based Method for Eddy Current Charac⁃terization of a Plate［J］.NDT&E International，2015，74（9）：66-71.

［4］郑岗，刘丁，张震，等.基于提离点的脉冲涡流测厚研究［J］.仪器仪表学报，2008，29（8）：1745-1749.

［5］Cong Sen，Gang Tie.Ultrasonic Thickness Measurement for Alu⁃minum Alloy Irregular Surface Parts Based on Spectral Analysis［J］.Transactions of Nonferrous Metals Society of China，2012，22（S2）：323-328.

［6］Jiang Hui，Zhu Jingtao，Wang Zhanshan，et al.Determination of Layer-Thickness Variation in Periodic Multilayer by X-Ray Re⁃flectivity［J］.Journal of Applied Physics，2010，107（10）：103523.

［7］Sekine Y，Soyama H.Using an Eddy Current Method with Inverse Analysis to Determine the Thickness of the Layer Modified by Cavitation Peening at the Surface of Type 316 L Austenitic Stain⁃ less Steel［J］.NDT&E International，2012，46（3）：94-99.

［8］Moulder J C，Uzal E，Rose J H.Thickness and Conductivity of Me⁃tallic Layers from Eddy Current Measurements［J］.Review of Sci⁃entific Instruments，1992，79（6）：3455-3465.

［9］黄平捷，张光新，吴昭同，等.多层导电结构厚度电涡流检测正向模型及仿真器研究［J］.传感技术学报，2005，18（3）：601-606.

［10］周德强，吴佳龙，王俊，等.碳纤维增强复合材料冲击缺陷脉冲涡流无损检测仿真与实验研究［J］.传感技术学报，2015，28（5）：671-676.

［11］Tian Guiyun，He Yunze，Adewalea I et al.Research on Spectral Response of Pulsed Eddy Current and NDE Applications［J］.Sen⁃sors and Actuators A—Physical，2013，189（1）：313-320.

［12］周德强，尤丽华，张秋菊，等.碳纤维增强复合材料脉冲涡流无损检测仿真与实验研究［J］.传感技术学报，2014，27（2）：277-282.

［13］Tai C C，James H R，John C M.Thickness and Conductivity of Me⁃tallic Layers From Pulsed Eddy-Current Measurements［J］.Re⁃view of Scientific Instruments，1996，79（11）：3965-3972.

［14］Shin Y K，Choi D M，Kim Y J，et al.Signal Characteristics of Dif⁃ferential-Pulsed Eddy Current Sensors in the Evaluation of Plate Thickness［J］.NDT&E International，2009，42（3）：215-221.

［15］Suresh K，Uma G，Umapathy M.A New Resonance-Based Method for the Measurement of Nonmagnetic-Conducting-Sheet Thickness［J］.IEEE Transactions on Instrumentation and Measurement，2011，60（12）：3892-3897.

［16］Zhang Jianhai，Yuan Maodan，Song Sung Jin，et al.Precision Mea⁃surement of Coating Thickness on Ferromagnetic Tube Using Pulsed eddy Current Technique［J］.International Journal of Preci⁃sion Engineering and Manufacturing，2015，16（8）：1723-1728.

［17］Angani C S，Park D G，Kim C G，et al.The Pulsed Eddy Current Differential Probe to Detect a Thickness Variation in an Insulated Stainless Steel［J］.Journal of Nondestructive Evaluation，2010，29（4）：248-252.

杨盼盼（1992-），女，山东淄博人，硕士研究生，主要研究方向为脉冲涡流厚度测量理论及应用，15190670636@163.com；

曹丙花（1981-），女，山东新泰人，博士，副教授，主要研究方向为电磁无损检测理论及应用，caobinghua2004@163.com；

范孟豹（1981-），男，山东聊城人，博士副教授，主要研究方向为电磁无损检测理论及应用，wuzhi3495@cumt.edu.cn。

EEACC：513010.3969/j.issn.1004-1699.2016.06.006

脉冲涡流厚度检测仿真与实验研究*

杨盼盼1，曹丙花2*，范孟豹1，谢伟1
（1.中国矿业大学机电工程学院，江苏徐州221116；2.中国矿业大学信息与电气工程学院，江苏徐州221116）

基于瞬态磁场的轴对称特性，利用有限元方法建立了脉冲涡流厚度检测的理论模型。仿真分析了被测金属板材在不同电导率和厚度参数时的探头差分信号并选择探头差分信号峰值作为信号特征。经分析发现：电导率一定时，差分信号峰值随被测金属板材厚度的增加呈递增趋势；被测金属板材厚度相同时，电导率越大差分信号峰值就越大。运用建立的试验系统进行实验研究，结果表明，实验与仿真结论一致，表明了所建模型的正确性和仿真结果的可信性。

无损检测；厚度检测；脉冲涡流；有限元仿真；峰值

TG115.28

A

1004-1699（2016）06-0821-05

2015-08-12修改日期：2016-02-29

项目来源：国家自然科学基金项目（5107172）；博士学科点专项科研基金项目（20120095120027）；江苏省大人才高峰项目（ZBZZ-041）；轻工过程先进控制教育部重点实验室开放课题项目（APCL11404）