展开锁定对太阳电池阵驱动机构的冲击载荷分析与测量

吴远波，陈重华，陈 汀

（上海卫星工程研究所，上海 201109）

展开锁定对太阳电池阵驱动机构的冲击载荷分析与测量

吴远波，陈重华，陈 汀

（上海卫星工程研究所，上海 201109）

太阳电池阵在空间会以较大的速度展开到位并锁定，这会给太阳电池阵的对日定向驱动机构（SADA）带来一定的冲击载荷，而仅依靠软件仿真很难得到准确可靠的冲击载荷数据。文章提出在卫星星体与太阳电池阵根部铰链之间串接一个测量工装，通过测量工装产生的应变可间接获得冲击载荷。该技术措施已在型号研制中得到应用，为驱动机构承载能力的设计分析和考核提供了依据。

太阳电池阵；对日定向驱动机构；冲击载荷；应变测量

0 引言

为满足卫星大功率的需求，必须有大面积的太阳电池阵供电［1］。由于受到卫星与运载火箭整流罩之间包络空间的限制，卫星发射前太阳电池阵须呈收拢状态，待整流罩抛射或星箭分离后，再展开到所需的位置。为了满足太阳电池阵展开要求，其展开驱动力/力矩必须大于阻力/阻力矩［2］；因此，在空间真空和微重力环境下，太阳电池阵会以较大的速度展开，且展开到位后瞬间完成锁定，这会给对日定向驱动机构（SADA）带来一定的冲击载荷。

SADA属于单点失效件，始终处于旋转运动状态，一旦发生故障，则会导致任务失败。相关资料表明，国内外多颗卫星在轨运行过程中因 SADA出现了卡死或短路故障而直接影响了整星的正常工作。因此，在 SADA地面研制过程中必须对其承受冲击载荷的能力进行分析和试验考核。为了获得太阳电池阵展开锁定对 SADA的冲击载荷，本文提出通过应变测量间接获取冲击载荷的方案。

1 仿真分析

1.1基板和连接架的柔性模拟

基板和连接架展开锁定时满足的动力学方程为

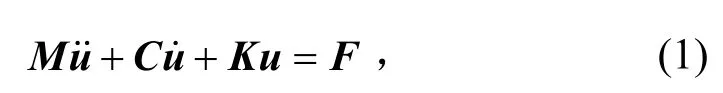
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；u为位移矩阵；F为力矢量。

取其固定界面的正则振动模态和相对于界面坐标的约束模态构成Craig-Bampton模态，即：

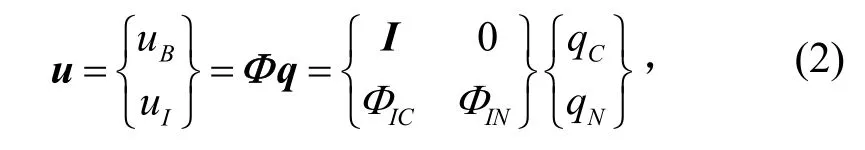
式中：Φ为模态矩阵；I为单位矩阵；q为模态位移。

对Craig-Bampton模态进行正交化处理，得到正交化的模态矩阵Φ*为

使用Nastran软件工具计算基板和连接架正交化的Craig-Bampton模态，并导入ADAMS中，作为基板和连接架的柔性模型。

第三，农村经济产权制度的完善使农村的经济得到快速发展。在这一改革当中，最为核心的内容就是确保农村经济产权交易平台的构建与完善，确保农村经济产权能够实现投资、交易以及增值，实现整个农村集体经济的保持与增长。

1.2铰链的模拟

将所有展开驱动弹簧简化为线性弹簧［3］，并考虑铰链转动过程中的摩擦阻力矩和板间电缆的阻力矩。其中摩擦阻力矩假设为常值，在确定展开驱动力矩大小时考虑该值；板间电缆的阻力矩假设为线性变化，展开状态为0，收拢状态最大，可在驱动弹簧的刚度设计中考虑该阻力矩。

1.3联动装置中绳索柔性的模拟

为考虑联动装置中绳索柔性的影响，将联动装置的作用简化为相应的力矩。设绳索的预紧力为P，相连的两个绳轮a、b的半径为ra和rb，单侧联动绳索的柔度系数为f，则绳索作用在两个轮上的扭矩分别为：

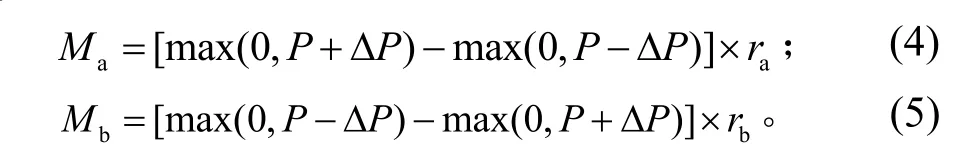
其中：ΔP=（θbrb-θara）/f ，θa为绳轮a的展开转动角度，θb为绳轮b的展开转动角度。

1.4分析结果

基于上述模型，使用ADAMS软件对太阳电池阵展开和锁定过程进行数值仿真，其结果见表 1。太阳电池阵坐标定义参见图1。

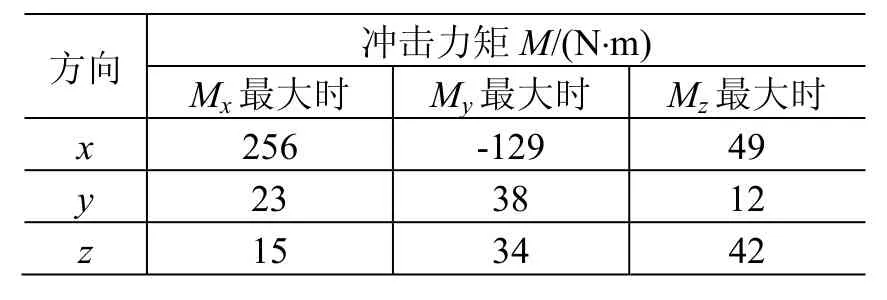
表1　根部铰链锁定对驱动机构的冲击力矩Table 1 Shock torque on SADA due to root hinge locking

图1　太阳电池阵坐标定义Fig. 1 Coordinate definition of the solar array

2 测量方案

根据仿真分析的结果来看，SADA承受的冲击载荷主要为展开方向产生的弯矩，即绕x轴的最大冲击载荷值远大于其他两个方向。为了简化试验方案，可忽略其他两个方向的载荷影响，主要测量绕x轴的冲击载荷。

在模拟墙与太阳电池阵根部铰链之间串接一个测量工装，并在测量工装上粘贴16个单向应变测点（应变测点的分布如图2所示）。测量工装主要由安装法兰和4根矩形测量杆（a， b， c， d）组成，在 4根测量杆上距离太阳电池阵对接面的 L1、L2处，各布置一组8个应变测点，总共16个测点。两组测点相对于测量杆截面的位置完全相同，各应变测点均用于测量各测量杆轴线方向的应变。

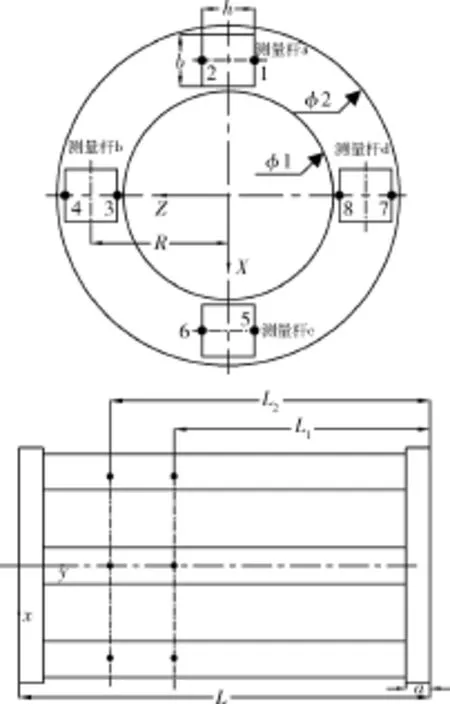
图2　测量工装应变测点布局Fig. 2 Arrangement of strain measurement points

根据测量工装的受力特性，每根杆截面上的应力可以等效为轴向力 fy、剪切力qz、弯矩Mx，其表达式见式（6）和式（7）。

其中：∆ε为2点与1点之差、4点与3点之差、6点与5点之差、8点与7点应变之差的一半。

在L1截面处，根据y向力平衡和弯矩平衡，

可得到：

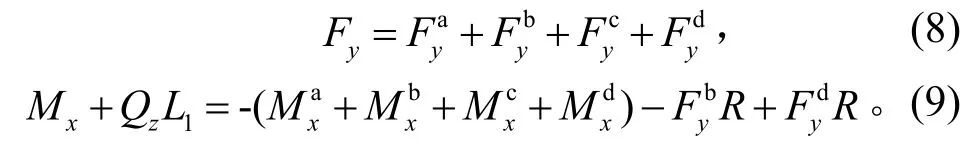
同样在 L2截面处，也可以列出两个方程。将式（6）、（7）分别代入式（8）、（9）中，可以得到轴向力Fy；将截面L1和L2处的弯矩平衡方程联立，可以解出弯矩Mx。

3 太阳电池阵冲击试验

太阳电池阵展开冲击试验时，通过悬挂式展开试验装置与支架车、模拟墙配合，模拟太阳电池阵在轨失重（近似零重力）状态，见图3。在测量工装上粘贴应变测点的实物照片见图4。

图3　太阳电池阵展开锁定冲击试验示意Fig. 3 Schematic diagram of solar arrays’ deploying/locking impact testing

开时间比真空中要长，地面展开试验所获得的力学参数会小于实际真空中的展开情况［4］，所以太阳电池阵展开锁定冲击试验分2种工况进行：首先进行常温常压下的展开试验；接着调整铰链展开盘簧力矩，使太阳电池阵地面展开时间尽量接近在真空中的展开时间（分析值）。每种工况展开试验分别进行4次。

图4　测量工装上粘贴应变片Fig. 4 Photo of strain measurement points on testing device

某型号太阳电池阵展开锁定冲击试验的弯矩数据分析汇总见表2，从试验数据分析可以得出如下结论：1）太阳电池阵展开锁定对SADA的冲击弯矩与展开时间成反比，两者之积大约为 2100～2200N·m·s；2）太阳电池阵在轨展开时间若按8.5s计算，则冲击弯矩约为 247～259N·m，比预分析结果（218N·m）至少大13%。

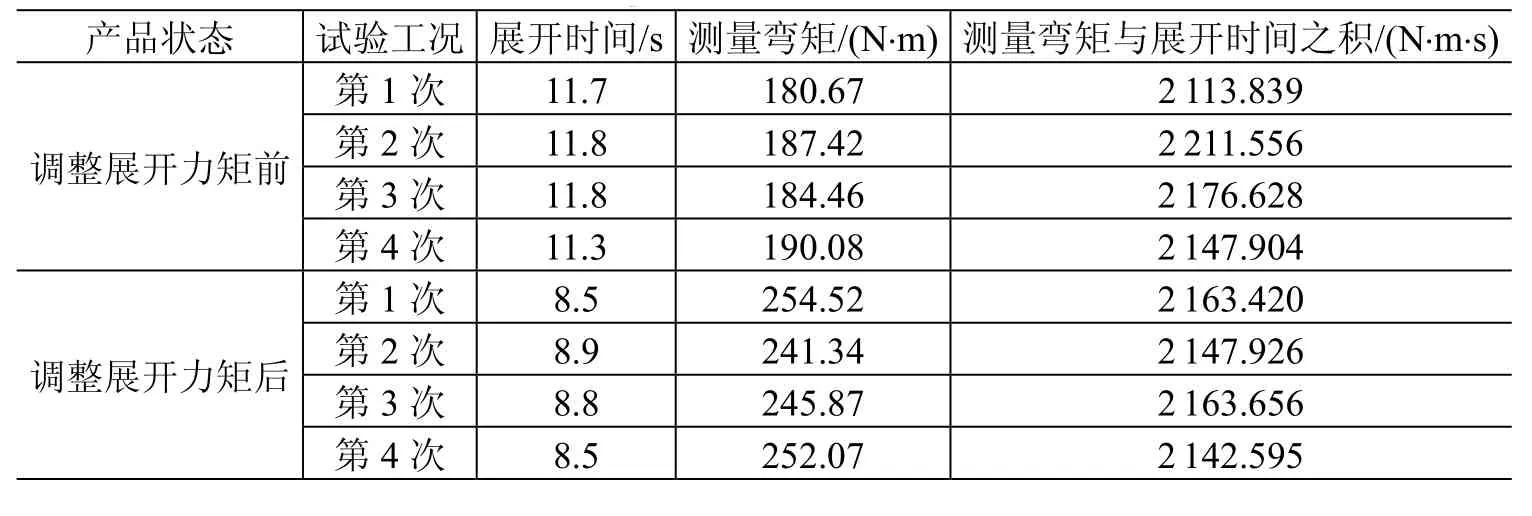
表2　太阳电池阵闭锁冲击试验数据Table 2 Experimental results of shock load

4 结束语

本文通过对 SADA在太阳电池阵展开锁定过程中承受的冲击载荷仿真分析与试验测量，得出了太阳电池阵展开锁定冲击弯矩与展开时间成反比的结论。根据太阳电池阵地面展开时间，可以较准确地预测太阳电池阵在轨展开锁定冲击载荷，为驱动机构地面试验考核提供依据，目前已经在部分型号上得到了应用和推广。

由于太阳电池阵的材料及各构件连接关系复杂，尤其铰链的非线性特性［5-6］，以及展开过程涉及刚柔耦合等［7-8］，使得试验结果与仿真结果存在一定差异，有必要进一步开展仿真与试验的研究。

（References）

［1］ 陈烈民. 航天器结构与机构［M］. 北京:中国科学技术出版社， 2005:101-108

［2］ 徐福祥. 卫星工程［M］. 北京:宇航出版社， 2002:20-25

［3］ 吴远波， 杜江华. 太阳电池阵铰链机构刚度等效方法［J］.航天器环境工程， 2010， 27（4）:467-471 WU Y B， DU J H. Stiffness equivalent method for the hinge mechanism of solar cell array［J］. Spacecraft Environment Engineering， 2010， 27（4）:467-471

［4］ 李淑娟， 苏里， 唐国安. 太阳能电池阵在空气介质中展开的动力学仿真［J］. 振动与冲击， 2002， 21（4）:106-107 LI S J， SU L， TANG G A. Deployment simulation of a solar array on the ground［J］. Journal of Vibration and Shock， 2002， 21（4）:106-107

［5］ 王巍， 于登云， 马兴瑞. 航天器铰接结构非线性动力学特性研究进展［J］. 力学进展， 2006， 36（2）:233-238 WANG W， YU D Y， MA X R. Advances and trends of non-linear dynamics of space joint-dominated structure［J］. Advances in Mechanics， 2006， 36（2）:233-238

［6］ 张永， 彭向中. 固定太阳翼展开后外弯基频的工程计算［J］. 宇航学报， 2010， 31（1）:50-54 ZHANG Y， PENG X Z. Engineering-approximate method of the first mode frequency of deployed solar wings without yokes［J］. Journal of Astronautics， 2010，31（1）:50-54

［7］ 马尚君， 刘更， 罗浩. 铰链展开式构型航天器设计及其动力学仿真［J］. 中国空间科学技术， 2010， 30（6）:79-84 MA S J， LIU G， LUO H. Design and dynamic simulation of hinged deployable configuration spacecraft［J］. Chinese Space Science and Technology， 2010， 30（6）:79-84

［8］ 游斌弟， 王兴贵， 陈军. 卫星太阳阵展开锁紧过程冲击振动［J］. 机械工程学报， 2012， 48（21）:67-76 YOU B D， WANG X G， CHEN J. Vibration and impact for deployable solar array of satellite with locking hinges［J］. Chinese Journal of Mechanical Engineering，2012， 48（21）:67-76

（编辑：肖福根）

Analysis and measurement of shock load on SADA due to solar array deployment locking

WU Yuanbo， CHEN Chonghua， CHEN Ting
（Shanghai Institute of Satellite Engineering， Shanghai 201109， China）

The solar array has to be locked in a specified position after deployment. The locking process produces a large shock on the SADA of the satellite. Accurate related results are difficult to be obtained from the commercial software simulations. This paper proposes a measurement method by connecting a measuring tool between the satellite body and the root hinge of the solar array. The strain data can be measured from the tool and the shock load can be calculated indirectly. The method is validated in the satellite development.

solar array； SADA； shock load； strain measurement

V41

A

1673-1379（2016）04-0378-04

10.3969/j.issn.1673-1379.2016.04.007

2016-03-22；

2016-07-11

吴远波（1978—），男，硕士学位，高级工程师，研究方向为卫星总体、结构机构设计与分析。E-mail:yuanbowu509@sina.com。