利用线性相关性证明离散型随机变量的独立性

梁瑞时（韶关学院数学与统计学院，广东韶关512005）

利用线性相关性证明离散型随机变量的独立性

梁瑞时
（韶关学院数学与统计学院，广东韶关512005）

利用行列向量的线性相关性证明二维离散型随机变量的独立性.结合两变量的边缘分布律所组成的矩阵的秩，并辅以相关的实例，拓展了独立性的证明方法.

矩阵；线性相关；离散型随机变量；相互独立

在概率论的各种版本的随机变量的独立性的判断中，对于离散型随机变量来说，最为常用的便是根据定义求得二维离散型随机变量的边缘分布，再由边缘分布的乘积等于联合分布来判断［1］，（X，Y）的联合分布律P｛X=xi，Y=yj｝=Pij，i，j=1，2，…时，其两个边缘分别是：

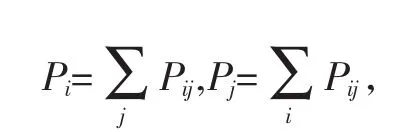
定理1 若X与Y相互独立，则总有矩阵B的两行（或两列）元素对应成比例.

由两行向量线性相关性，则可推出在矩阵B中最少可有一非零行（或列）向量，设αi为非零行向量，则由线性相关的性质［2］可知，其余行向量均可由αi线性表出.也即为αj=kiαi.则矩阵B可变为：

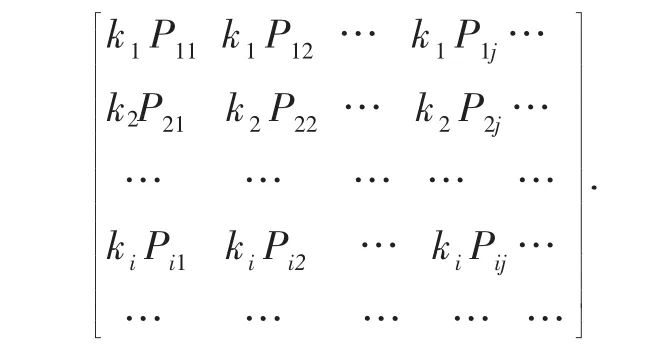
其中，Pij=kiP1j（i，j=1，2，…），并且则两随机变量的边缘分布为［3］：

因此有：

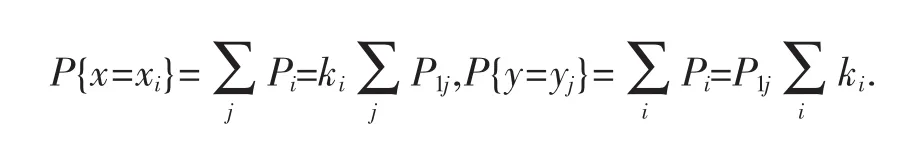
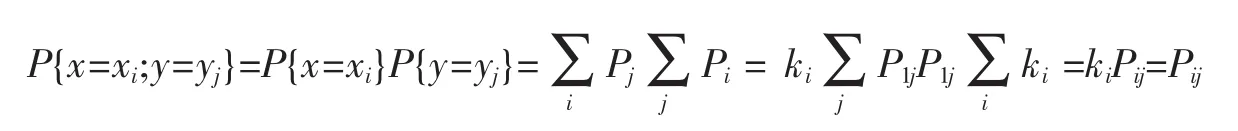
也即二维随机向量X，Y相互独立［4］.所以由两随机变量联合分布律所组成的矩阵B中的向量组（α1，α2，…，αi，…）或（β1，β2，…，βj，…），（i，j=1，2，…）必线性相关，由线性相关性质可推出该矩阵的任意两行向量（或列向量）必对应成比例.

定理2若以P（xi，yj）=Pij组成的矩阵的秩为1，则随机变量X、Y相互独立.

证如r（B）=1，则可知矩阵B可表为一m维列向量αm（α1，α2，…，αm，…）T与一n维行向量β1×n=（β1，β2，…，βj，…）的乘积，也即B=αβ.

因此：

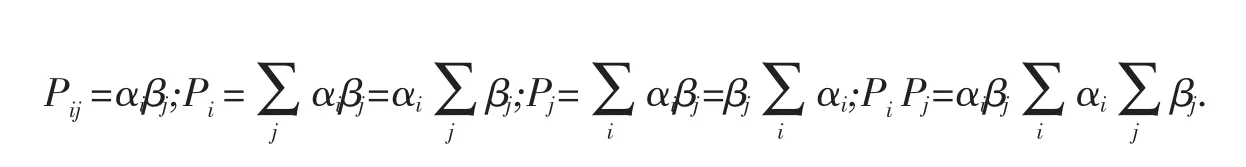
例1给定两变量X，Y的分布律，如表1所示，问X与Y相互独立否［5］？

表1　变量X，Y的分布律

证 由两随机变量的联合分布律所组成的矩阵的任意两行（或两列）都不对应成比例，所以该矩阵线性无关，由定理可得两变量X与Y不相互独立.

例2给定两变量X，Y的分布律，如表2所示，问X与Y相互独立否？

表2　变量X，Y的分布律

证 由P｛Y=-1｝以及P｛Y=1｝所在的两列对应成比例，可得该矩阵线性相关，变量X与Y相互独立.

［1］彭刚，禹辉煌.二维离散型随机变量独立性判别定理及应用［J］.湖南理工学院学报，2010，23（2）:23-25.

［2］赵立军.线性代数［M］.上海:复旦大学出版社，2013.

［3］韩旭里，谢永钦.概率论与数理统计［M］.上海:复旦大学出版社，2009.

［4］马双红.随机变量独立性判断的一个充要条件［J］.兰州理工大学学报，2012，38（6）:146-148.

［5］李德新，陈聪.随机变量独立性判别法［J］.高等数学研究，2008（4）:54-55.

The Linear Correlation for Proving Independence of Two-Dimensional Discrete Random Variable

LIANG Rui-shi
（School of Mathematics and Statistics，Shaoguan University，Shaoguan 512005，Guangdong，China）

This paper uses linear correlation matrix to prove the independence of the two-dimensional discrete random variables.Combined with the edge of the two variables distribution law of matrix rank，supplemented by relevant examples，the paper expands the proof method of independence.

matrix；Linear correlation；Discrete random variables；independence

O211

A

1007-5348（2016）06-0006-03

（责任编辑：邵晓军）

2016-05-13

梁瑞时（1980-），女，广东阳江人，韶关学院数学与统计学院助教，硕士；研究方向：数学统计.