基于加速k均值的谱聚类图像分割算法改进*

李昌兴， 黄艳虎， 支晓斌， 谢笑娟

(1.西安邮电大学 理学院，陕西 西安 710121；2.西安邮电大学 通信与信息工程学院，陕西 西安 710121)



基于加速k均值的谱聚类图像分割算法改进*

李昌兴1， 黄艳虎2， 支晓斌1， 谢笑娟1

(1.西安邮电大学 理学院，陕西 西安 710121；2.西安邮电大学 通信与信息工程学院，陕西 西安 710121)

对谱聚类图像分割算法进行改进，即引入加速 均值算法替换原算法中的k均值算法，得出加速谱聚类的图像分割算法。将改进算法应用于微软剑桥研究院Grab cut数据集中的5幅实验图像，结果显示：在平均区域一致性评价不降低的前提下，改进算法完成分割所花费的平均时间比改进前可缩短58 %。

图像分割； 谱聚类； 加速k均值； 加速谱聚类

0　引　言

图像分割是计算机视觉领域的重要组成部分[1]。谱聚类算法[2]在图像分割和特征提取方面应用广泛[3]。

谱聚类算法能在任意形状的样本空间上聚类，且收敛于全局最优解[4]，将谱聚类算法应用于图像分割，通常能取得很好的分割效果[5]，但同时它也有着自身的缺陷—计算相似性矩阵高度复杂，问题的求解会变得异常费时[6]。文献[7]中提出基于路径的相似性度量，但对边界点过于敏感，分割耗时不理想；文献[8]提出基于密度敏感的相似性度量，但当位于高密度区的两个样本数据点穿过的路径较长时，效果尚不明显，并且最终采用k均值聚类简化后的向量空间，造成聚类耗时过长。本文对谱聚类图像分割算法进行了改进，即引入加速 均值替换原有算法中的k均值算法，得出加速谱聚类的图像分割算法。

1　谱聚类算法与 均值算法

1.1谱聚类算法

给定n个数据点x1,x2,…,xn，谱聚类算法构建了一个相似性矩阵，它反映了xi与xj之间的关系。然后，它使用相似性信息，将x1,x2,…,xn聚类成k个簇[9]。谱聚类有很多种解释，最常用的就是基于图切的理论。它要求将谱聚类转化为求出数据集的Laplacian矩阵，然后再求该矩阵的特征向量，进而对特征向量进行聚类[10]。其算法流程如下：

1)计算数据间的相似性矩阵W=(wij),其中,wij=exp(‖xi-xj‖22σ2),(i,j=1,2,…，n)。

3)计算Laplacian矩阵L，一般取L=D-1/2WD-1/2。

4)计算矩阵L的前k个特征值所对应的特征向量v1,v2,…,vk。

5)将v1,v2,…,vk按列组成矩阵V∈Rn×k。

6)对于i=1,2,…,n,令yi∈Rk是对应于V的第i行所构成向量。

7)将点yi(i=1,2,…,n)用k均值算法聚类成簇C1,C2,…,Ck。

谱聚类算法有着它自身的缺陷。当将谱聚类算法用于图像分割时，一般是以图像的像素作为输入数据，而一幅图像像素通常在百万以上，这时，相似性矩阵的计算，存储以及特征值求解都面临着巨大的困难[11]，导致计算时间过长。目前通用算法最后一步都是以k均值算法对拉普拉斯矩阵进行聚类，如能将k均值算法替换成比k均值更快的加速k均值算法，那么可对谱聚类算法的收敛速度起到一定的增幅作用。

1.2k均值算法

k均值算法在模式识别中被叫做Lloyd算法[12]，其算法的两个主要步骤：

1)对n个数据点X={x1,x2,…,xn}任意选择k个对象作为初始聚类中心c1,c2,…,ck， 计算每对x和c之间的距离，分配x到其最接近的聚类中心。

2)重新计算每个聚类的均值作为新的聚类中心。

k均值算法虽然是迄今为止使用最广泛的一种聚类算法，但当它处理巨量数据时，由于要计算多中心点之间的距离且需要许多次迭代来达到收敛，k均值算法非常缓慢。文献[13]提出了一种利用三角不等式来加速经典k均值算法。

2　加速谱聚类算法

2.1加速k均值算法

在k均值中大多数的距离计算在算法中是多余的。如果一个点远离一个中心，就没必要为了知道这个数据点不属于这个中心而计算它们之间的距离。相反，如果一个点比任何其他点更接近一个中心，也就没有必要为了知道这个数据点应该被分配到这个中心而计算它们之间精确的距离。令x是任何数据点，c是当前为x分配的簇中心，并设c′是任何其他中心。

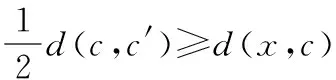
如果知道d(x,c)的上限为u(x)，且

则

则不必计算d(x,c′)。

又设c′为某个簇的中心，该簇中包含数据点x，c″为前一次迭代过程中的中心点。如果

d(x,c″)≥l(x,c″)

则

d(x,c′)≥max{0,d(x,c″)-d(c′,c″)}

≥max{0,l(x,c″)-d(c′,c″)}

=l(x,c′)

如果d(x,c)的上限u(x)与d(x,c′)的下限l(x,c′)存在，并且

u(x)≤l(x,c′)

则

d(x,c)≤u(x)≤l(x,c′)≤d(x,c′)

加速k均值法可以描述如下：

初始化：选择初始中心。对于每个数据点x和中心c，设定下限

l(x,c)=0

分配每个x到其最近的初始中心

c(x)=argmincd(x,c)

每当d(x,c)被计算时，令

l(x,c)=d(x,c)

上限

u(x)=mincd(x,c)

下面，重复直到算法收敛。

2)确定所有满足u(x)≤s(c(x))的x点。

3)对于所有剩余的点x和中心c必满足

c≠c(x)

u(x)>l(x,c),

三个条件。

1)如果r(x)为真，则计算d(x,c(x))和令

r(x)=false;

否则

d(x,c(x))=u(x)

2)如果

d(x,c(x))>l(x,c)

或者

则计算d(x,c)，如果

d(x,c)

令

c(x)=c

4)对于每个中心c，让m(c)为被分配到c点的平均值。

5)对于每个点的x和中心c，分配

l(x,c)=max{l(x,c)-d(c,m(c)),0}。

6)对于每个点x，分配

u(x)=u(x)+d(m(c(x)),c(x)),

r(x)=true。

7)用m(c)替换每个中心c。

2.2加速谱聚类算法

对谱聚类图像分割算法进行如下改进，即引入加速k均值替换原有算法中的k均值算法，得出加速谱聚类的图像分割算法。其算法步骤如下：

1)依次计算相似性矩阵W、度矩阵D以及拉普拉斯矩阵L。

2)计算L的前k个特征值所对应的特征向量v1,v2,…,vk，并将它们按列组成矩阵V。

3)对V的n个行向量执行加速k均值，聚类成簇C1,C2,…,Ck。

3　实验结果

计算机配置为酷睿2代处理器，2.2 GHz主频，4 GB内存以及320 GB硬盘。算法实现基于Win7操作系统，仿真软件由Matlab2010b。

图1～图5给出了两种谱聚类的分割效果，其中(a)选自微软剑桥研究院Grab Cut数据集[14]中的5幅作为原始图像。各图中(b)列为原谱聚类处理后的效果，(c)列为快速谱聚类算法处理后的效果。

图1　对蔬菜图像用不同算法分割的效果

图2　对大兵图像用不同算法分割的效果

图3　对树图像用不同算法分割的效果

图4　对工人图像用不同算法分割的效果

图5　对蘑菇图像用不同算法分割的效果

可以看出，加速谱聚类算法对图像的分割效果与原谱聚类相当。客观地，用区域一致性[15]对两种算法进行评价如表1，数据显示，5幅图像的区域一致性平均提高了0.004 %，新算法完全可以胜任图像分割的要求。

表1　算法的区域一致性评价

表2给出了两种算法的运行时间。

表2　算法运行时间表

表2是两种算法分别对每幅图像运行20次，记录两种算法对上述5幅图像的平均分割时间。从表2可以看出，加速谱聚类算法能够有效地减少图像分割所用的时间，其中，最差的蘑菇图像，用了原谱聚类运行时间的54 %，而树木图像，更是只用了原谱聚类运行时间的36 %。通过计算，五幅图像平均花费时间缩短了58 %。

4　结束语

本文通过引入加速k均值替换原有算法中的k均值算法，对原谱聚类算法进行了改进，得出加速谱聚类的图像分割算法。新算法应用于实验图像，取得了非常好的效果，在分割效果保持基本不变的情况下，分割所用耗时缩短 58 %。因此改进后的快速谱取类算法具有高效的分割特性。

[1]关昕,周积林．基于改进谱聚类的图像分割算法[J]．计算机工程与应用,2014,50(21):184-188．

[2]章毓晋.图像工程[M].3版.北京:清华大学出版社,2013:5-6.

[3]陈姿羽,黄靖,李伟鹏.一种改进的自适应谱聚类图像分割算法[J].南方医科大学学报,2012, 32(5):655-658.

[4]高琰,谷士文,唐琎,等.机器学习中谱聚类方法的研究[J].计算机科学,2007,34(2):201-203.

[5]贾建华,焦李成.空间一致性约束谱聚类算法用于图像分割[J].红外与毫米波学报,2010,29(1):69-74.

[6]葛芳,王年,郭秀丽.一种改进的谱聚类算法及其在基因表达谱分析中的应用[J].安徽大学学报,2012,36(5):67-72.

[7]Chang H,Yeung D Y.Robust path-based spectral clustering[J].Pattern Recognition,2008,41(1):191-203.

[8]王玲,薄列峰,焦李成.密度敏感的谱聚类[J].电子学报,2007,35(8):1577-1581.

[9]赵凤,范九伦,支晓斌,等.灰度和空间特性的谱聚类图像分割[J].西安邮电学院学报，2012，17(1):52-57.

[10] Bühler T,Hein M.Spectral clustering based on the graph p-Laplacian[C]∥Proceedings of the 26th Annual International Confe-rence on Machine Learning,New York:ACM,2009:81-88.

[11] 董安国,薛方.基于随机谱聚类的图像分割算法[J].数学的实践与认识,2013,43(23):169-174.

[12] Hamerly G.Makingk-means even faster[C]∥SIAM International Conference on Data Mining,Ohio:SDM,2010:130-140.

[13] Elkan C.Using the triangle inequality to acceleratek-means[C]∥Proceedings of the 20th International Conference on Machine Learning(ICML),WA,2003:147-153.

[14] 索利姆.Python计算机视觉编程[M].北京:人民邮电出版社,2014:216-218.

[15] 李学俊,刘祥俊,赵礼良.基于梯度熵的Otsu图像分割算法[J].计算机工程与设计,2015,36(3):705-709.

黄艳虎，通讯作者，E—mail:869489894@qq.com。

Improvements of accelerationk-means based spectral clustering algorithm for image segmentation*

LI Chang-xing1, HUANG Yan-hu2, ZHI Xiao-bin1, XIE Xiao-juan1

(1.School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China;2.School of Communication and Information Engineering,Xi’an University of Posts and Telecommunication,Xi’an 710121,China)

A spectral clustering algorithm for image segmentation is achieved by improving spectral clustering algorithm for image segmentation,that is,introduce accelerationk-means algorithm to replace the originalk-means algorithm.The improved algorithm is applied in five experimental images from the Grab Cut dataset of Microsoft Research at Cambridge,results show that time consuming of image segmentation by the improved algorithm can be shortened by 58 % in the premise of average area of conformance assessment without reducing.

image segmentation; spectral clustering; accelerationk-means; acceleration spectral clustering

10.13873/J.1000—9787(2016)09—0137—04

2015—10—27

陕西省自然科学基金资助项目(2014JM8307)； 陕西省教育厅科学研究计划资助项目(14JK1661)

TP 391

A

1000—9787(2016)09—0137—04

李昌兴(1962-),男，陕西户县人，教授，从事数字图像处理研究。