几何扩展卡尔曼滤波算法在卫星姿态确定系统中的应用*

江　丹, 邓新蒲, 吴　京, 莫邵文, 杨媛媛

(国防科学技术大学 电子科学与工程学院,湖南 长沙 410073)



几何扩展卡尔曼滤波算法在卫星姿态确定系统中的应用*

江丹, 邓新蒲, 吴京, 莫邵文, 杨媛媛

(国防科学技术大学 电子科学与工程学院,湖南 长沙 410073)

卡尔曼滤波因其良好的性能广泛应用于卫星姿态确定中。经典的扩展卡尔曼滤波(EKF)算法在估计姿态坐标系中表示估计误差矢量，由于没有考虑到估计姿态坐标系与真实姿态坐标系之间存在偏差，从而导致姿态估计精度下降。针对这个问题，Andrle M S通过几何变换引入误差一致性表示，在此基础上，提出了几何扩展卡尔曼滤波(GEKF)算法，将姿态误差四元数和陀螺漂移增量通过几何变换进行一致性表示，解决了估计误差矢量表示不一致的问题。本文介绍了误差一致性表示的原理，并将GEKF算法应用于含常值漂移与时间相关漂移的陀螺模型中，仿真实验表明：GEKF算法比MEKF对陀螺漂移的估计更加精确，在滤波精度上取得了明显改善。

姿态确定； 卡尔曼滤波； 误差一致性； 陀螺漂移

0　引　言

利用星敏感器和陀螺进行组合来确定卫星的姿态已经得到广泛应用，陀螺能够以较高的频率对卫星平台的三轴角速度进行测量，并通过积分得到姿态角。 但是陀螺的漂移使测量误差随时间累计，这会严重影响测量的精度。星敏感器测量精度高，没有误差累积和漂移现象，其缺陷是测量频率较低[1]。因此，将星敏感器和陀螺进行组合来确定卫星的姿态可以克服各自的缺陷，实现优势互补。

常用的姿态表示方法有欧拉角、四元数、旋转矢量法和修正的罗德里格参数(modified Rodrigue parameters,MRP)等[2,3]，四元数因其具有较小维数且无奇异值的出现而被广泛应用于卫星姿态确定算法中。然而，在传统的扩展卡尔曼滤波(extended Kalman filtering,EKF)算法中并没有解决四元数的归一化约束问题。乘性EKF(multiplicative EKF,MEKF)算法将姿态四元数表示为误差四元数与估计四元数的乘积解决了四元数归一化约束问题[4,5]，其算法的主要思想是利用EKF算法对四元数的矢量部分进行估计，同时利用校正的四元数来表示卫 满足四元数单位化约束，又可以避免滤波过程中出现奇异值。

在实际应用中，由于不知道真实的卫星姿态，EKF等算

法通常将误差矢量表示在估计姿态坐标系中。需要注意的是,真实的姿态坐标系与估计姿态坐标系之间是存在偏差的，将矢量及其估计值表示在估计坐标系中，矢量将会因两个坐标系之间的偏差而产生一定的偏移，如果坐标系之间的偏差值较大，建立在这种矢量误差定义基础上的EKF等算法其估计精度将会受到严重影响。针对这个问题，Andrle M S在姿态确定问题中引入了一种误差一致性表示方法[6,7]，通过几何变换将状态误差矢量表示为真实坐标系下，基于该方法提出了用于姿态确定的几何EKF(geometric EKF,GEKF)算法[6]。文献中仅给出了常值漂移陀螺漂移模型下的算法。本文首先介绍误差一致性表示的原理，然后将其应用于含常值漂移与指数漂移的陀螺模型中，推导了该应用下的GEKF算法，并完成了该应用下GEKF算法与MEKF算法仿真比较。

1　姿态确定的数学模型

1.1陀螺测量模型

理想情况下，陀螺的测量值正比于卫星本体相对于惯性系的转速沿陀螺输入轴的分量。但是在实际中，陀螺受自身设计、工作机理、运动环境等的影响，不可避免会存在误差。

陀螺的测量模型[8,9]为

ωg=ω+d+b+ηv

(1)

式中ω为真实的角速度， d为陀螺的时间相关漂移，b为陀螺常值漂移，ηv为测量噪声，建模为零均值高斯白噪声。d,b满足如下方程

(2)

式中ηd,ηb为零均值高斯白噪声，-Dτ为相关时间常数τ构成的对角阵。

将噪声写成如下的矢量形式

w=[ηvηdηb]T

(3)

协方差为E{w(t)wT(τ)}=Q(t)δ(t-τ)。其中

1.2星敏感器测量模型

星敏感器以恒星作为测量基准，得到星敏感器的三轴姿态，经变换得到卫星本体坐标系的姿态。然而在工程应用中由于安装误差等影响，星敏感器测量值不可避免地存在误差，实际的星敏感器的测量模型[10,11]如下

b=Ar+ν

(4)

式中b为卫星本体坐标系中的矢量，r为参考坐标系中的矢量，A为从参考坐标系到卫星本体坐标系的姿态旋转矩阵，ν为量测误差，建模为零均值高斯白噪声。

1.3姿态运动学方程

姿态四元数定义如下[13]

q=[ρTq4]T

(5)

式中ρ为四元数的矢量部分，q4为四元数的标量部分。利用四元数表示的姿态矩阵为

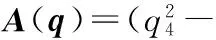
(6)

由平台的姿态四元数q和姿态角速度ω描述的平台姿态运动的姿态运动学方程为[13]

(7)

式中

(8)

2　误差一致性表示原理

在姿态确定的EKF算法中，对于模型(1)～(7)定义

(9)

式中

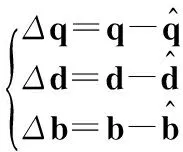
(10)

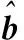
minE{ΔxTΔx}

(11)

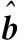
(12)

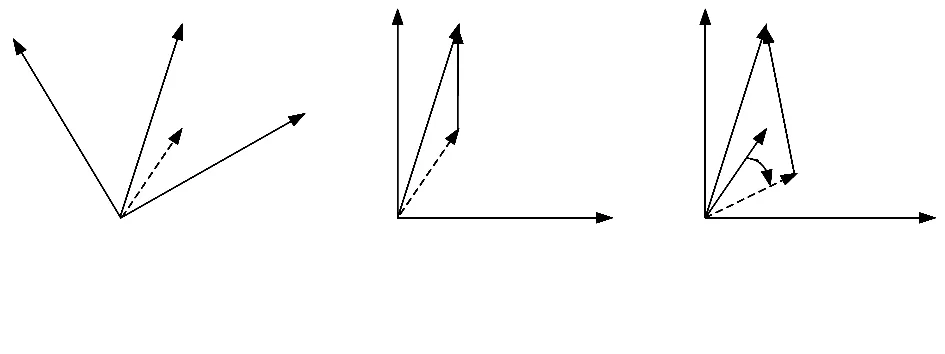
图1　误差矢量一致与非一致表示

记一致表示方式下b,d真值与估计值误差矢量为db,d d，由图1(c)可知，通过几何变换得到db与Δb之间的关系式如下

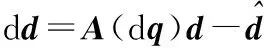
(13)

同理有

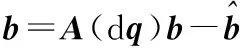
(14)

记

d q=[d ρTdq4]T

(15)

式中dρT为误差四元数的矢量部分，当dq很小时

下式成立

dα≈2dρ

(16)

式中dα为姿态角误差矢量。推导得到

A(dq)≈A(dα)≈I3×3-[dα×]

(17)

定义

dx=[dαTddTddT]T

(18)

推导可得

Δx=Cdx

(19)

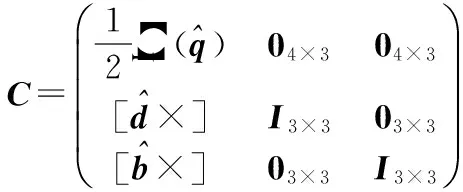
3　GEKF算法

文献[7]根据前述的误差一致性表示原理提出了GEKF算法，本节并将GEKF算法推广应用于含常值漂移与时间相关漂移的陀螺模型中。

3.1状态变量与状态方程

传统的EKF算法将姿态四元数，陀螺的漂移量作为状态变量。即x=[qTdTbT]T。运动学方程近似为

(20)

式中线性化矩阵

在GEKF算法中，使用误差一致性表示方法来定义误差矢量，此时的状态误差矢量定义为

d x=[d αTd dTd bT]T

(21)

可得运动学方程的微分形式

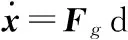
(22)

式中

(23)

(24)

3.2测量变量与测量方程

取两个星敏感器输出光轴矢量作为测量值

则测量方程为

zk=hk(xk)+vk

(25)

式中hk(xk)=A(qk)rk。

3.3滤波算法

1)预测

MEKF算法其状态转移矩阵为

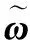
将其离散化得到差分形式的状态转移矩阵

ΦMEKF=I+FΔt+F2Δt2

(26)

式中Δt为采样周期。

相应的GEKF算法其状态转移矩阵为

Φk=T-1ΦMEKFT

(27)

式中

(28)

(29)

状态变量的预测值为

(30)

预测误差协方差矩阵Pk/k-1可由式(30)求解

(31)

2)增益

卡尔曼增益为

(32)

式中

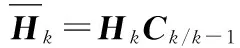
(33)

3)更新

状态变量增量为

(34)

状态变量更新为

(35)

姿态四元数归一化

(36)

误差协方差的更新值为

(37)

式中

(38)

4　仿真分析

本仿真实验基于GEKF算法进行，将星敏感器和陀螺的测量值经不同滤波算法得到卫星平台的姿态。将仿真结果与经典的MEKF算法进行比较。

4.1参数设置

传感器的测量噪声和滤波初值如表1所示。

表1　算法参数设置

4.2仿真分析

分别对MEKF算法与GEKF算法进行仿真，取1 000次Monte—Carlo仿真结果进行统计，得到不同算法的均方根误差、相应的姿态角估计和陀螺漂移估计。

表2给出了不同算法的姿态角均方根误差。

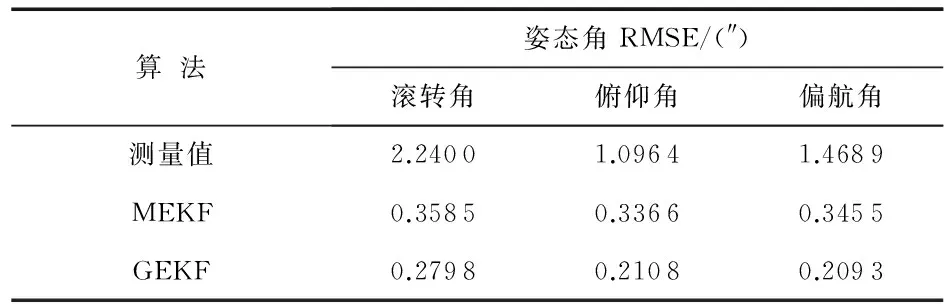
表2　不同算法的RMSE

从表2可以看出，在相同的仿真条件下，GEKF算法与MEKF算法相比，姿态角估计RMSE明显降低。

图 2、图3分别给出了不同算法的姿态角估计与姿态角估计误差。

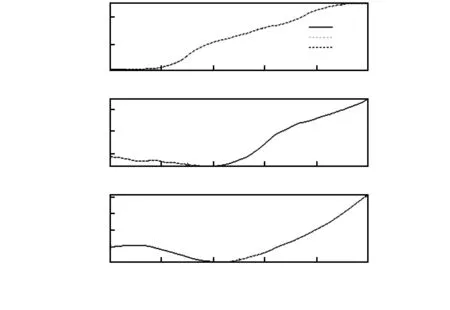
图2　姿态角估计

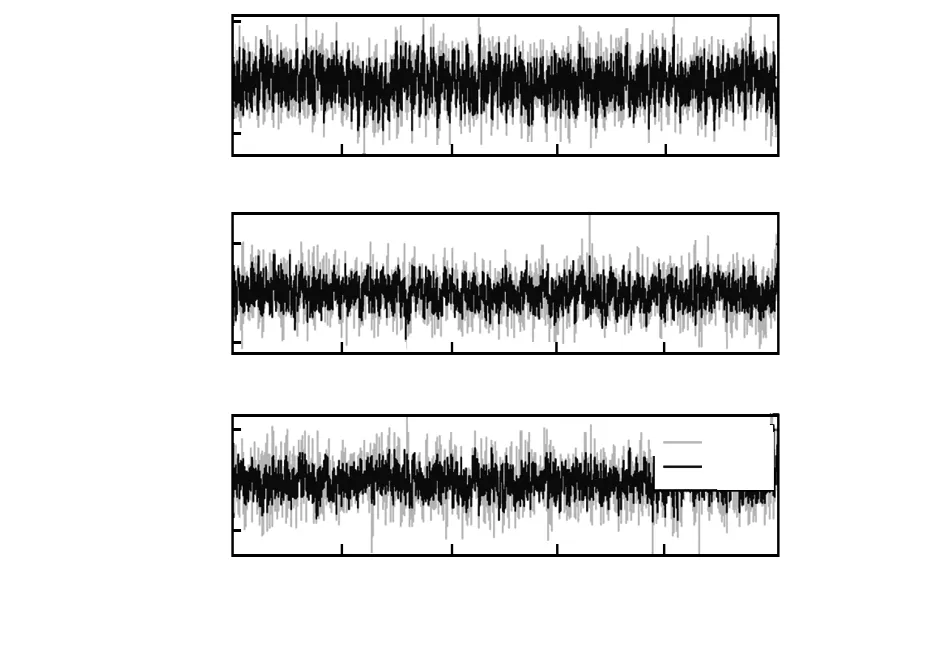
图3　姿态角估计误差

从图2可以看出两种算法都能估计出平台的姿态角，图3给出了两种算法的姿态角估计误差，从中可以看出，使用GEKF算法可以使姿态角估计误差保持在±0.6″以内，而使用MEKF算法得到的姿态角其估计误差在±1.2″范围内波动。

图4给出了不同算法的陀螺漂移估计。

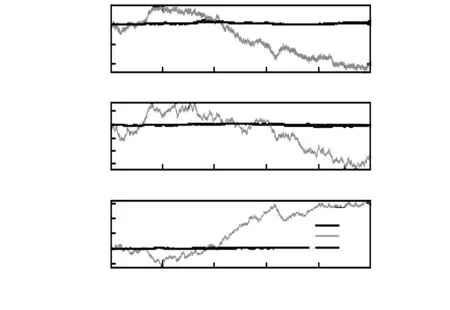
图4　陀螺漂移估计

从图4可以看出，GEKF算法对陀螺漂移的估计相对于MEKF算法更加精确。

5　结　论

本文针对传统的MEKF算法中矢量误差表示不一致的问题，将GEKF算法应用于卫星姿态确定系统中。该算法首先将误差矢量在估计姿态坐标系下进行一致性表示来解决误差矢量表示不一致的问题，然后对重新定义的状态误差矢量进行EKF滤波来估计出姿态四元数增量和陀螺漂移增量，并通过姿态修正得到卫星的姿态。仿真实验表明:GEKF算法能够精确地估计出陀螺的常值漂移和时间相关漂移，并且在滤波精度上较MEKF有明显改善。

[1]吕振铎.雷拥军.卫星姿态测量与确定[M]．北京：国防工业出版社,2013．

[2]Crassidis J L,Markley F L,Cheng Y．A survey of attitude estimation methods[J]．Journal of Guidance,Control,and Dynamics,2007,30(1):12-28．

[3]Karlgaard C D,Schaub H.Nonsingular attitude filtering using modified rodrigues parameters[J]．The Journal of the Astronauti-

cal Sciences，2009,57(4):777-791．

[4]Markley F L,Crassidis J L．Fundamentals of spacecraft attitude determination and control[M].New York:Springer,2014．

[5]Farrenkopf R L．Analytic steady-state accuracy solutions for two common spacecraft attitude estimators[J]．J Guid Contr,1978,1(4):282-284．

[6]Andrle M S,Crassidis J L.Attitude estimation employing commom frame error representations[C]∥JAIAA Guidance,Navigation,and Control Conference,2016．

[7]Andrle M S，Crassidis J L．Geometric integration of quaternion-s[J]．Journal of Guidance Control and Dynamics，2013,36:1762-1767．

[8]Markley F L.Attitude error representations for Kalman filte-ring[J].Journal of Guidance，Control and Dynamics，2003,26(2):311-317.

[9]郭晓鸿,杨忠,陈喆.EKF和互补滤波器在飞行姿态确定中的应用[J].传感器与微系统,2011,30(11):149-152.

[10] Shuster M D．Kalman filtering of spacecraft attitude and the QUEST model[J].Journal of the Astronautical Sciences，1990,38(3):377-393．

[11] Shuster M D,Oh S D.Three-axis attitude determination from vector observations[J].Journal of Guidance and Control,1981,4(1):70-77．

[12] Markley F L,Crassidis,J L．Fundamentals of spacecraft attitude determination and control[M].New York:Springer,2014．

[13] Shuster M D,A survey of attitude representations[J].Journal of the Astronautical Science,1993,41(4):439-517．

Application of geometric extended Kalman filtering algorithm in satellite attitude determination system*

JIANG Dan, DENG Xin-pu, WU Jing, MO Shao-wen, YANG Yuan-yuan

(College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073,China )

Kalman filtering is widely used in satellite attitude determination because of its good performance.The classical EKF algorithm represents the estimated error vector in the estimated attitude coordinate system,because there is no consideration to estimate the deviation between the attitude coordinate system and the true attitude coordinate system,which leads to decrease of attitude estimation precision.To solve this problem,Andrle M S introduces error consistent represent method through geometric transformation,and on this basis,he proposes GEKF algorithm attitude error quaternion and gyro drift increment through geometric transformation of consistency representation,solve the problem that estimate error vector representation is not consistent.The principle of error consistency representation is introduced,and apply GEKF algorithm to gyro model with constant drift and time drift.Simulation experiments show that the GEKF algorithm is more accurate than MEKF on gyro drift estimation,and filtering precision is improved significantly.

attitude determination; Kalman filtering; error consistency; gyro drift

10.13873/J.1000—9787(2016)09—0156—05

2015—06—14

国家自然科学基金资助项目(61401474)

TP 212

A

1000—9787(2016)09—0156—05

江丹(1991-),男，安徽安庆人，硕士研究生，主要研究方向为卫星姿态确定。