新建铁路隧道上跨既有公路隧道控制爆破安全距离研究
2016-09-08赵丰薛亚东李硕标赵瀚翔
赵丰,薛亚东,李硕标 ,赵瀚翔
(1. 同济大学 岩土及地下工程教育部重点实验室,上海 200092;2. 同济大学 地下建筑与工程系,上海 200092)

新建铁路隧道上跨既有公路隧道控制爆破安全距离研究
赵丰1, 2,薛亚东1, 2,李硕标1, 2,赵瀚翔1, 2
(1. 同济大学 岩土及地下工程教育部重点实验室,上海 200092;2. 同济大学 地下建筑与工程系,上海 200092)
新建塔石岭铁路隧道上跨既有公路隧道,采用全断面爆破施工,为了确保既有公路隧道运营的安全,需要明确控制爆破开挖的安全施工距离。基于已有的岩体中爆破振动速度衰减理论模型,首先计算安全施工距离范围,为验证模型与参数的合理性,开展相应的有限元计算分析。计算结果得出了爆破距离与既有隧道衬砌拱顶振动速度的关系,据此可根据振动速度安全标准计算得到相应的爆破施工安全距离,从而为工程爆破设计提供科学依据。
交叉隧道;控制爆破;安全距离
随着我国交通运输事业的迅猛发展,越来越多的隧道工程投入建设。在近距离交叉隧道爆破施工对既有隧道的影响方面,国内外学者做了大量研究[1-3],采用数值模拟的方法对爆破过程中既有隧道的振动响应做了详细分析[4-6],但对于上跨隧道控制爆破安全距离的研究还比较少。在保证既有隧道运营安全的前提下,如何合理控制上跨隧道控制爆破施工的距离对缩短工程工期、减少工程造价有着直接的影响。

临近工程爆破不可避免会对既有的岩石产生振动影响,振动冲击波可能导致隧道结构发生损坏或者出现衬砌掉块,严重威胁隧道运营安全[8]。对于爆破振动的影响评价因素(或指标),许多国家,如中国、美国、德国、瑞典等,采用质点振动速度作为衡量爆破振动效应的标准。大量现场试验和观测表明,爆破振动破坏程度与质点速度的相关性最好,且与其他物理量相比,振速与岩土性质有较稳定的关系[9],因而学者提出了施工控制的重点是爆破振动的影响[10-13]。有关爆破振动速度的研究,目前主要有实测法、经验公式法以及数值模拟法等。考虑爆破设计的安全与合理,本文通过理论分析计算上跨隧道的安全施工距离,并通过数值模拟,分析不同爆破工况下既有隧道二次衬砌控制点的振速变化规律,从而把握新建隧道控制爆破施工的安全距离范围[11]。
1 工程概况
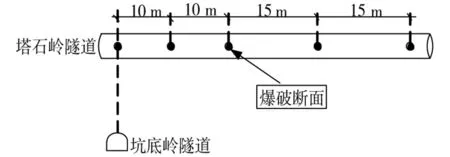
拟建塔石岭隧道位于浙江省龙泉市龙泉镇境内,为铁路单线单洞隧道,隧道全长3672.89m,断面底宽7.6m,高8.5m,受路线的总体走向和地形地貌等条件控制,该隧道设计路线在里程DK151+185处上跨既有公路(S228省道)坑底岭隧道,坑底岭隧道底宽11m,高7m,两隧道呈64°斜交,最短垂直距离为17m,交叉处地质条件为Ⅲ级围岩,具体如图1所示。为了减少对既有隧道的影响,需要在两隧道交叉点处一定范围内进行控制爆破,综合考虑造价、工期等各方面因素,控制爆破安全距离的选取是工程设计的关键。
2 理论分析
根据《爆破安全规程》(GB6722-2011)[7],对于交通隧道,规定安全振动速度应小于15cm/s。考虑到既有隧道已运营多年,衬砌强度有所下降,且隧道交叉区域附近存在断层构造,因此建议本工程既有隧道衬砌的振动速度不大于5cm/s。
对于爆破振动波在传播过程中的衰减规律已有如下研究:

图1 隧道位置剖面图Fig.1 Cross section of tunnel position
1)萨道夫斯基公式
苏联科学家萨道夫斯基由试验归纳出与岩石介质性质、爆源有关的系数K和衰减指数α,得到目前工程爆破计算地面振动速度普遍采用的经验公式:
(1)
式中:v为地面质点峰值振动速度(cm/s); Q为爆破装药量kg;齐发爆时取为总药量,分段爆破时取为最大一段药量;R为测点距爆源中心的距离m;K为与岩石性质、爆破参数和方法有关的系数;a为爆破振动波隧距离衰减的指数。
我国《爆破安全规程》[7]列出了K和a的计算选取范围(见表1)。K和a的取值也可以通过不同岩石的类型选取[8]。
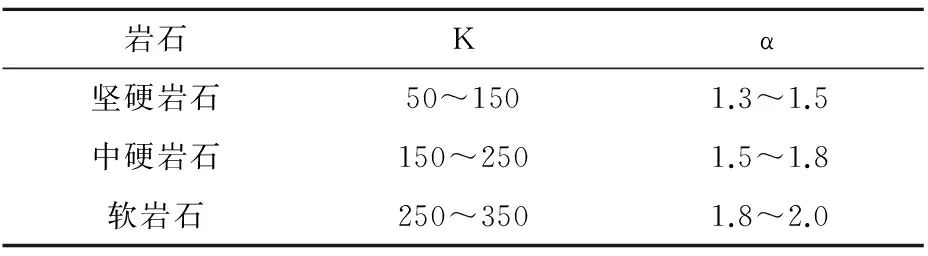
表1 K 值和α值与岩石的关系
2)美国矿业局对20个采石场和建设工地的爆破振动观测数据进行了分析,提出了振速的计算公式:
(2)
式中:K和α分别为现场的特征系数和衰减指数,其他符号意义同前。
3)P.B.Attwell(奥特维尔)等人对欧洲采石场的爆破振动观测数据进行了统计分析,提出的振速公式如下:
v=K(Q/R2)α
(3)
式中符号意义同前。
4)日本旭化成工业株式会社提出:
(4)
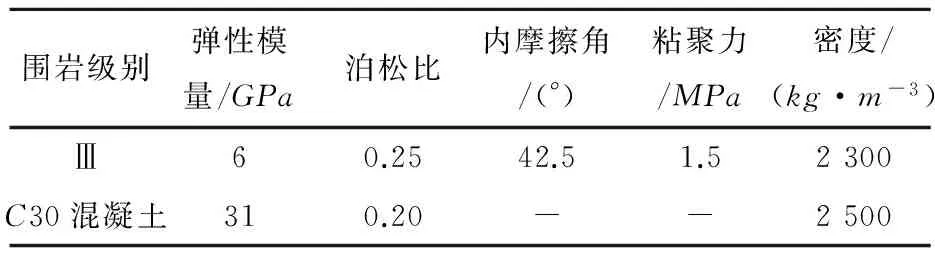
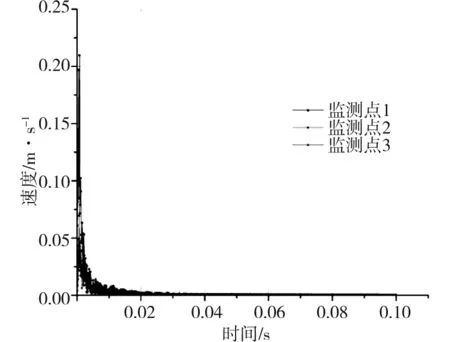
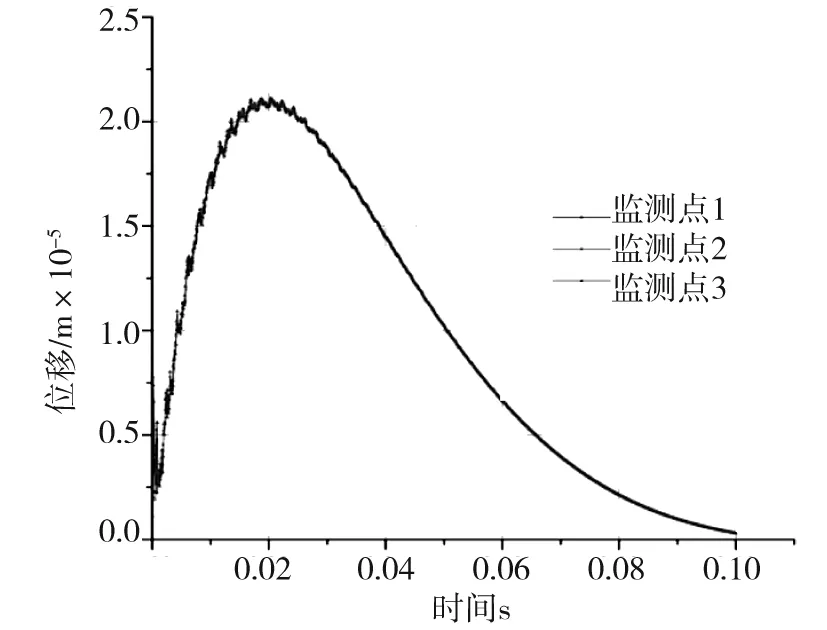
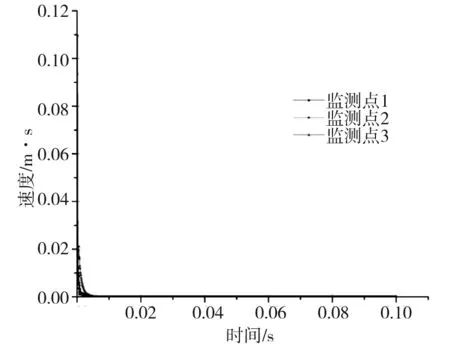
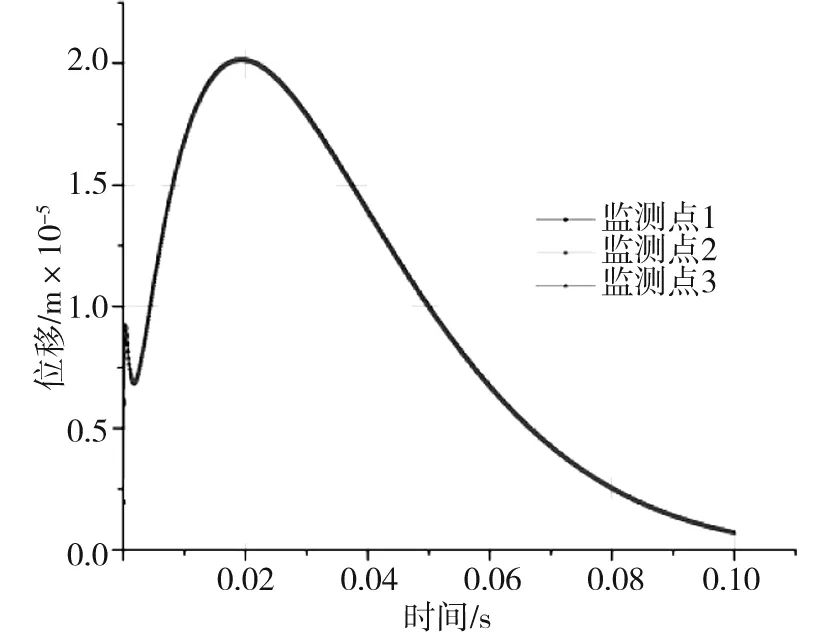
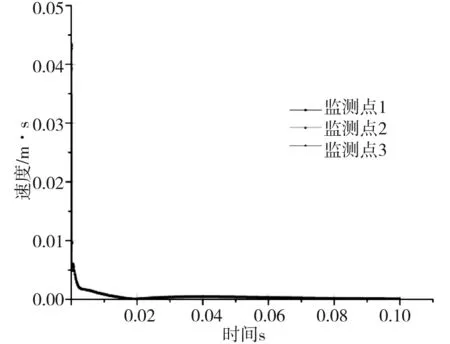
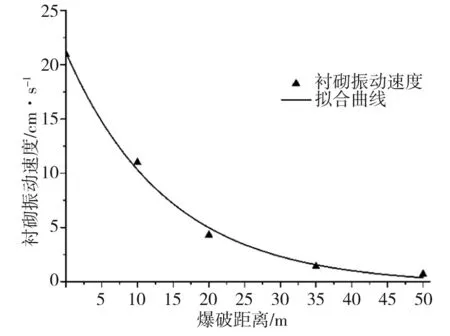
式中:K是与爆破条件、地质条件有关的系数,掏槽爆破时,K=500~1 000;台阶爆破时K=200~500;α为指数,爆区为黏土层时α=2.5~3.0,爆区岩石时,α=2.0;R为测点距爆源中心的距离m,30m 根据建议标准,控制既有隧道二次衬砌的振动速度为5cm/s。交叉处地质条件为Ⅲ级围岩,参考表1可得到K与α的取值范围,根据现场的钻孔资料以及在现场所做的地层声波测试[12],并结合以往的工程经验,可大致估计所在地层的完整性。本工程计算参数取值如下:K=200~220,α=1.6,该工程分段爆破最大单段药量为Q=16kg。利用上述4个公式分别反算得到的控制爆破安全距离范围见表2。 表2 计算得到的控制爆破安全距离 3.1模拟方案 为了进一步研究新建隧道爆破开挖距离对既有隧道的影响,并与已有经验公式相互验证,采用MIDAS/GTS/NX大型数值模拟软件进行模拟计算。根据相关资料和爆破计算理论,分别设置在隧道交叉点正上方开挖、距正上方右侧10m开挖、距正上方右侧20m开挖、距正上方右侧35m开挖和距正上方右侧50m开挖五种种模拟方案,每种方案全断面开挖的进尺为3m。模拟计算方案示意图见图2。 图2 模拟计算方案示意图Fig.2 Simulation calculation program diagram 3.2有限元模型 根据本工程中隧道的尺寸、间距、以及爆破振动影响的范围,确定模型长×宽×高=150m×100m×87m,计算模型网格见图3。 图3 有限元网格图Fig.3 FEM model 3.3模型参数 模型中围岩及隧道衬砌的物理力学参数见表3。 表3 有限元分析参数表 3.4监测点布置 模拟时,在既有公路隧道拱顶的衬砌上沿纵向布置3个监测点,监测新建隧道爆破开挖过程中对既有隧道衬砌的影响,测点间距25m,测点2位于两隧道交叉处正下方,监测点布置见图4。 3.5本构模型的选取 Hoke-Brown本构模型广泛应用于岩石力学工程,但在实践中所需的扰动因子D和地质强度指标GSI2个参数比较难以准确获取。利用扰动岩体波速Vp和岩石纵波波速比值的平方计算扰动因子D,利用岩体纵波波速Vp与岩体RMR值的关系来计算岩体的GSI值,推导得到改进后的Hoke-Brown本构模型: 图4 监测点布置图Fig.4 Arrangement of monitoring points (5) (6) (7) (8) 定义扰动因子: (9) 式中,σc为岩石的单轴抗压强度;Vi、Ei和kvi分别为岩体波速、变形模量和完整性系数;V0和E0分别为岩石(岩块)波速、变形模量。一般情况下,取i=1,V1、E1和kv1分别表示岩体的波速、变形模量和完整性系数;在多次扰动(多次爆破)情况下,取i=2,3,4…n,分别表示在多次(i-1次)扰动后岩体的波速、变形模量和完整性系数等性质。 3.6边界条件 在数值模拟计算边界条件方面,有固定边界,黏性边界和弹性边界。结合衢宁铁路塔石岭隧道采用爆破施工,爆破振动波对于固定边界会引起振荡反射波,导致计算结果失真,因此采用黏弹性边界较为适合。黏性采用比较通用的瑞利(Rayleigh)阻尼,根据文献[5]确定临界阻尼ξmiin=0.01,体系基频ϖ0=50Hz。 3.7模型加卸荷计算 爆破动载的模拟,通常采用在设置的爆破区域边界上施加相同当量的爆破动压力荷载,美国公路研究所(NationalHighwayInstitute(US),1991)建议考虑爆破振动衰减随时间作用的动压力公式: (10) (11) 式中:Pdet为爆破荷载kN/m2;PB为作用在孔壁面上的退耦爆破压力MPa; Ve为爆破速m/s;dc为装药直径mm;dh为装药孔直径mm;Sge为容重kN/m3。 在上述公式的基础上,考虑时间函数关系,Statfield提出了改进爆破荷载计算公式: (12) 式中:B为荷载系数,为每1kg装药量产生的动压力,可取16 338。单段药量的荷载见图5。 图5 爆破荷载历程Fig.5 History of blasting load 4.1正上方开挖 塔石岭隧道掌子面在已建隧道正上方以全断面法爆破施工,既有隧道衬砌上3个监测点处的振动速度时程曲线如图6所示。衬砌位移量时程曲线如图7所示。 图6 振动速度时程曲线Fig.6 Vibration velocity time history curve 图7 衬砌位移量时程曲线Fig.7 Lining displacement time history curve 正上方3m进尺全断面开挖时,既有隧道衬砌振动速度最大值达到20.95cm/s,超过了建议的允许振动速度, 既有隧道衬砌位移最大值达到2.109×10-5,变形不会影响既有隧道安全。 4.2右侧10 m开挖 塔石岭隧道掌子面在已建隧道右侧10m处全断面法爆破施工,既有隧道衬砌上3个监测点处的振动速度时程曲线如图8所示。衬砌位移量时程曲线如图9所示。 图8 振动速度时程曲线Fig.8 Vibration velocity time history curve 正上方右侧10m处3m进尺全断面开挖时,既有隧道衬砌振动速度最大值达到11.00cm/s,超过建议的允许振动速度, 既有隧道衬砌位移最大值达到2.011 5×10-5,变形不会影响既有隧道安全。 4.3右侧20 m开挖 塔石岭隧道掌子面在已建隧道右侧20m处全断面法爆破施工,既有隧道衬砌上3个监测点处的振动速度时程曲线如图10所示。衬砌位移量时程曲线如图11所示。 图9 衬砌位移量时程曲线Fig.9 Lining displacement time history curve 图10 振动速度时程曲线Fig.10 Vibration velocity time history curve 图11 衬砌位移量时程曲线Fig.11 Lining displacement time history curve 正上方右侧20m处3m进尺全断面开挖时,既有隧道衬砌振动速度最大值达到4.30cm/s,小于建议的允许振动速度。既有隧道衬砌位移最大值达到7×10-6,不会影响既有隧道安全。 通过数值模拟,可得到不同开挖距离下拱顶衬砌质点的振动速度,如表4所示。 表4 参数值分析 对模拟结果进行拟合,得到爆破距离与振动速度之间的关系曲线,如图12所示。 图12 衬砌振动速度与距离的拟合曲线Fig.12 Line of the fitting curve of velocity and distance 该拟合曲线的函数方程为: y=y0+A1e-x/t1 (13) 式中:x为爆破开挖的距离;y为既有隧道拱顶衬砌质点的振动速度;y0,A1和t1为常数,分别为-0.27,21.38和14.25,拟合相似度为0.99。 将理论模型计算的结果与数值分析模拟的结果进行比较,发现用萨道夫斯基计算得到的安全距离与模拟的距离最为接近,而用其他公式计算的距离与模拟有较大的偏差。 1)在正上方爆破开挖时,既有隧道衬砌振动速度的最大值达到20.952cm/s,在正上方右侧10m爆破开挖时,既有隧道衬砌振动速度的最大值达到11cm/s,均大于5cm/s;在正上方右侧20m爆破开挖时,既有隧道衬砌振动速度的最大值为4.3cm/s,小于5cm/s;在正上方右侧35m及50m爆破开挖时既有隧道衬砌振动速度远小于5cm/s。结合理论分析结果,建议在塔石岭隧道掌子面距离交叉点20m左右的范围内施工时,需采用控制爆破的方式以保证既有隧道的安全。 2)通过拟合曲线可得到爆破距离与既有隧道衬砌拱顶振动速度的关系,据此可根据振动速度安全标准计算得到相应的爆破施工安全距离,从而为工程爆破设计提供科学依据。 3)通过实例验证了爆破振动速度传播规律采用数值模拟与经验公式两种方法计算的合理性与各自的不足,建议在爆破振动分析中结合两种分析方法以取得可指导实践的结论。 [1] 叶培旭, 杨新安, 凌保林, 等. 近距离交叉隧洞爆破对既有隧道的振动影响[J]. 岩土力学, 2011, 32(2): 537-541 . YEPeixu,YANGXinan,LINBaolin,etal.Vibrationeffectsonexistingtunnelinducedbyblastingofanadjacentcrosstunnel[J].RockandsoilMechanics, 2011, 32(2): 537-541. [2]YANGRL,ROCQUEP,KATSABANISP,etal.Measurementandanalysisofnear-filedblastvibrationanddamage[J].GeotechnicalandGeologicalEngineering,1994,12:169-182. [3]Jong-HoShin,Hoon-GiMoon,Sung-EunChae.Effectofblast-inducedvibrationonexistingtunnelsinsoftrocks[J].TunnelingandUndergroundSpaceTechnology,2011,26:51-61. [4] 乔汝佳. 小净距爆破作用下隧道的动力响应研究 [D]. 西安: 西安建筑科技大学, 2013 . QiaoRujia.Studyoninfluenceofblastingvibrationontunnelsmallclearance[D].Xi’an:Xi’anUniversityofArchitectureandTechnology, 2013. [5] 潘小马. 临近隧道施工对既有隧道的影响[D]. 成都: 西南交通大学, 2002: 26 - 27. PanXiaoma.Influenceofanewtunnelconstructionontheadjacentexistingtunnel[D].Chengdu:SouthwestJiaotongUniversity,2002:26-27. [6] 醋经纬. 小净距交叉隧道爆破振动控制技术研究 [D]. 兰州: 兰州交通大学, 2014. CuJingwei.Researchonthecontroltechnologyofsmallcleardistancecrosstunnelblastingvibration[D].Lanzhou:LanzhouJiaotongUniversity, 2014. [7]GB6722—86,爆破安全规程[S]. GB6722—86,Blastingsafetyregulation[S]. [8] 周维垣. 高等岩石力学[M]. 北京: 水利水电出版社, 1989. ZHOUweiyuan.Advancedrockmechanics[M].Beijing:Water&PowerPress, 1989. [9] 汪旭光. 爆破设计与施工[M]. 北京: 冶金工业出版社, 2012. WANGxuguang.Blastingdesignandconstruction[M].Beijing:MetallurgicalIndustryPress, 2012. [10] 陈仕猛. 上下交叉隧道近接施工技术的研究[D].成都: 西南交通大学, 2008. CHENShimeng.Studyonconstructionschemeofup-down-crossingandsmallclear-spantunnels[D].Chengdu:SouthwestJiaotongUniversity, 2008. [11] 赵东平, 王明年. 小净距交叉隧道爆破振动响应研究[J]. 岩土工程学报, 2007, 29(1): 116-119. ZHAODongping,WANGMingnian.Studyoninfluenceofblastingvibrationoncrosstunnelswithsmallclearance[J].ChineseJournalofGeotechnicalEngineering, 2007, 29(1): 116-119 . [12] 闫长斌, 徐国元, 杨飞. 爆破动荷载作用下围岩累计损失效应声波测试研究[J]. 岩土工程学报, 2007, 29(1): 88-92. YANGChangbin,XUGuoyuan,YANGFei.Measure-mentofsoundwavestostudycumulativedamageeffectonsurroundingrockunderblastingload[J].ChineseJournalofGeotechnicalEngineering, 2007, 29(1) : 88-92. [13] 李玉峰, 彭立敏, 雷明锋. 交叉隧道工程设计施工技术研究进展[J]. 铁道科学与工程学报, 2014, 11(1): 67-78. LIyufeng,PENGlimin,LEImingfeng.Researchprogressinthedesignandconstructiontechnologyofcrossingtunnel[J].JournalofRailwayScienceandEngineering, 2014, 11(1): 67-78. Analysis on control blasting safety distance of the new railway tunnel overpasses the established highway tunnel ZHAO Feng1, 2,XUE Yadong1, 2,LI Shuobiao1, 2,ZHAO Hanxiang1, 2 (1.KeyLaboratoryofGeotechnicalandUndergroundEngineering(TongjiUniversity),MinistryofEducation,Shanghai200092,China;2.DepartmentofGeotechnicalEngineeringCollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China) ProposedTashilingrailwaytunneloverpassestheestablishedhighwaytunnelandisdesignedtoadoptthewholesectionblastingconstruction.Inordertoensurethesafetyoftheexistinghighwaytunneloperation,itisnecessarytodefinethesafetyconstructionofcontrolledblastingexcavationdistance.Basedontheexistingtheoreticalmodelofblastingvibrationvelocityattenuationinrockmass,itwasthefirsttocalculatethesafetyconstructionoftheprojectscope.Next,thecorrespondingfiniteelementcalculationandanalysiswereusedtoverifytherationalityofthemodelandparameter.Theresultsindicatetherelationshipbetweenexplosiondistanceandthevibrationvelocityofthetunnelvaultlining.Accordingtothesafetystandardsofvibrationvelocity,thecorrespondingblastingconstructionsafetydistancecanbeobtainedthroughcalculation,soastoprovidescientificbasisforengineeringblastingdesign. crossedtunnel;controlblasting;safetydistance 2015-08-12 浙江省交通厅科技资助项目(2015J22) 薛亚东(1971-),男,山西芮城人,副教授,博士,从事隧道及地下工程研究;E-mail:yadongxue@126.com TU455 A 1672-7029(2016)07-1365-07
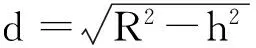
3 数值模拟



4 计算结果及分析


5 结论
