服役环境下材料蠕变对挤压筒过盈量的影响

李一红　罗远新　马　玲　宋宗焘　王勇勤

重庆大学，重庆，400030



服役环境下材料蠕变对挤压筒过盈量的影响

李一红罗远新马玲宋宗焘王勇勤

重庆大学，重庆，400030

在传统Lamé公式的基础上引入直接位移求解法(DDM)，推导了考虑蠕变效应的挤压筒应力/应变分布解析模型，分析了各层筒应力随时间的变化情况。针对挤压筒用热作模具钢H13进行了高温蠕变试验，获取了500 ℃下热作模具钢H13的蠕变行为和Norton表达式，探讨了材料蠕变对挤压筒各层之间过盈量的影响规律。研究结果表明，交界面处各层筒的蠕变应变有差别，造成径向变形不一，从而使得过盈量减小。

挤压筒；过盈量；蠕变；H13钢

0　引言

挤压产品因其加工过程材料损耗少、生产效率高、符合现代工业绿色低碳的发展趋势而得到广泛应用。大型挤压筒是重型挤压机的关键部件之一，其耐用性和服役寿命对挤压成本的影响很大。生产实践表明，由于长期承受循环高温高压的作用，故大型挤压筒的失效常表现为以下模式：蠕变疲劳损伤引起的内侧筒脱出、挤压筒变形断裂和由于摩擦等因素造成的内筒磨损失效等[1]，其中针对蠕变疲劳损伤引起的失效的相关研究还比较缺乏。Sommitsch等[2-3]对挤压筒材料进行了本构关系研究，并通过Deform-2D模拟挤压过程，获得坯料对筒体的作用力、温度等边界条件后将其导入到ABAQUS软件中，通过编写用户子程序UMAT或Z-mat实现对挤压筒损伤的计算及寿命的计算；Krumphals等[4-5]对挤压筒材料H11钢的微观性能演化进行了研究，采用Gleeble热模拟试验机对H11材料的高温性能进行试验，将得到的微观组织模型导入到热-力耦合有限元分析中，以实现对挤压筒蠕变疲劳失效的研究。Laue等[6]提出了多层筒过盈装配的计算方法。敖文刚等[7]在文献[6]方法的基础上，运用双剪统一强度理论优化了双层圆筒配合半径及过盈量，并运用ANSYS软件进行了实例分析。赵云路等[8]也通过单层和多层圆筒强度的理论分析计算，提出了挤压筒各层筒半径和过盈量的初步设计方法。谢水生等[9]、李燕等[10]运用有限元方法对过盈装配扁挤压筒进行结构分析，获得了不同装配参数下扁挤压筒在装配后及工作时应力和变形的变化规律。刘全坤等[11]结合数值模拟方法分析了扁挤压筒内孔变形规律，并基于Lagrange插值的变过盈量对扁挤压筒变形的影响和强度进行了分析。冯秋红等[12]综合运用了有限元法、BP神经网络和多目标遗传算法，在一定程度上实现了多目标优化下变过盈量扁挤压筒的等强度结构设计。以上研究均通过多组试验、多组推导并结合数值模拟来确定材料本构关系、微观组织模型和变形规律，耗时长、难度大，对挤压筒设计尤其是过盈量的选取等具有一定的参考意义。尽管挤压筒越来越多地采用数值方法进行校核，但是推导能用于优化挤压筒设计和装配参数的理论模型仍是十分必要的。Luo等[13]在Lamé公式基础上，提出一种直接位移求解法(directdisplacementmethod，DDM)计算各层筒间界面压力，该方法推导出挤压筒各衬半径(位移)随载荷的变化关系式，由位移协调条件计算出多层挤压筒配合面处的界面力，无需多次迭代，求解速度快，便于工程设计应用。

在内外筒温度接近的情况下，挤压筒蠕变变形不一致会使筒间过盈量减小，在外界摩擦作用下造成内侧筒的脱出[14]。因此，研究蠕变对挤压筒过盈量的影响规律十分重要。本文从理论分析与试验研究角度出发，针对蠕变对挤压筒过盈量的影响进行分析，以期为挤压筒设计提供新的理论基础。

1　挤压过程中挤压筒应力场演变模型

1.1挤压筒弹性设计理论模型

在线弹性设计理论中，几何参数与过盈量设计的前提是各层筒的应力值不得超过材料的屈服极限，即假设材料为线弹性体，不考虑材料屈服特性。传统叠加法求解应力分布流程复杂，需要多次迭代求解。DDM模型无需多次迭代，第i层筒内径/外径处的变形量分别为[13]：

(1)

其中，主要参数如图1所示。ri,in、ri,out分别为第i层筒的内径和外径，u为径向位移，pi,in为i-1层衬与i层衬间的界面力，pi,out为i层衬与i+1层衬间的界面力，Ei、μi分别为i层衬的弹性模量和泊松比。

图1　i层筒受力与变形图

i层筒的外径与i+1层筒的内径在挤压过程中应保持一致，如图2所示，位移协调条件表达式如下式所示：

ri,out+ui,out=ri+1,in+ui+1,in

(2)

其中，ri+1,in为第i+1层筒的内径，ui+1,in为第i+1层筒内径处的变形量。

边界载荷条件p0,1=0、pn,n+1=0对应过盈装配，p0,1=pi、pn,n+1=0对应挤压工况。其中，p0,1表示内筒内壁的边界载荷，pn,n+1表示最外层筒外壁的边界载荷。将边界载荷条件作为初始条件代入式(1)、式(2)，求解n-1个非线性方程得到对应界面处的界面力，进而利用Lamé公式求解得到各层筒的应力分布情况。

图2　位移协调条件

1.2挤压筒服役全过程应力场演变分析

对挤压筒进行蠕变变形分析时，必须考虑挤压时间对挤压筒的影响。传统计算方法(包括DDM)虽然可以实现对挤压筒受一定挤压力情况下的应力分布情况进行分析，但由于假定挤压力为静水压力，与轴向无关，故只能进行(r,θ)二维平面上的静态分析，由此计算得到的应力分布仅为静态分布，与挤压时间无法关联。因此，有必要对挤压筒内壁所受挤压力随时间的变化情况重新进行分析。

1.2.1挤压筒的边界条件

图3　挤压过程挤压筒边界载荷图

挤压筒在实际挤压过程中所受载荷边界条件十分复杂，存在坯料与挤压筒、挤压筒与外部机构之间的热-力耦合相互作用。为便于分析，结合文献[2,15]的研究成果，将此边界条件简化为图3所示斜坡载荷形式，包括起始段、斜坡段和平行段三段。沿径向以分段函数形式表示该斜坡载荷，表达式如下：

p=p(z,t)=

(3)

挤压筒边界载荷如图3所示。挤压过程描述如下：挤压筒仅受内压p的作用，挤压方向为z方向，挤压轴从起始位置坐标z0处以速度v挤压坯料，在挤压过程中，内压斜坡段长度为l，当坯料到达模具顶端zL处时，进入模具进行挤压，得到型材。

1.2.2挤压周期内的应力演变

边界条件确定以后，对任意时间t和轴向位置z下的挤压筒受力分析便可以根据DDM来进行。在内壁径向压力作用下，任意时刻内筒、中筒、外筒受力平衡且满足位移协调条件，求解过程如下。

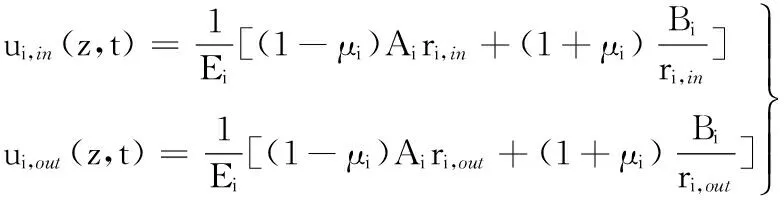
(4)

其中，pi-1,i、pi,i+1不再为常值，二者均为z、t的函数，需要注意的是，对内筒而言(i=1)，pi-1,i=p0,1=p，p表达式如式(3)所示；对外筒而言(i=n)，pi,i+1=pn,n+1=0。

联立式(2)～式(4)可求解得到与(z,t)相关的界面力(pi,i+1,pi-1,i)，将求得的界面力(pi,i+1,pi-1,i)代入下式，解得各层筒(z,r)位置、t时刻的应力：

(5)

式中，σi,r、σi,θ分别为第i层筒的径向应力和切向应力。

这样，在简化实际挤压工况条件下，就通过理论分析计算得到内力作用下应力随时间的演变规律。

2　蠕变试验

通过试验确定典型挤压筒材料H13热作模具钢(化学成分如表1所示)的蠕变变形规律。参照标准HB 5151-1996《金属高温拉伸蠕变试验方法》进行试验，试验温度500 ℃，选择600 MPa、800 MPa、1000 MPa载荷水平进行加载，保载时间定为100 h。选择三思CTM-B1型电子式高温持久蠕变试验机进行试验。

表1　H13化学成分　%

通过试验，得到500 ℃下不同应力水平下的三组试验数据，在总变形基础上减去温度和弹性变形得蠕变变形随时间的变化情况，如图4所示。试验1(保载应力σ=1000MPa)在73h时断裂。

1.σ=1000 MPa　2.σ=800 MPa　3.σ=600 MPa图4　蠕变曲线

由图4可以看出，蠕变曲线呈现出明显的两段：初始蠕变阶段和稳态蠕变阶段。第一阶段历时较短，忽略其影响而只考虑第二阶段作用。稳态蠕变率公式以Norton公式最为常用，主要用于分析蠕变的第二阶段，在温度一定的情况下，Norton公式可简写为：

(6)

因高温下挤压筒长期处于稳态蠕变阶段，假定挤压筒温度恒定为500 ℃，该情况下选择式(6)进行蠕变率的计算最为合适。式(6)中B、n值的确定流程如下：由图4可知，三条不同应力下的曲线大致在20h后达到稳态，即其应变速率值保持不变。因此，可将20h后的蠕变曲线视作蠕变稳态阶段，并对稳态蠕变阶段的三条曲线分别进行线性拟合，结果如图5所示。得到对应于600MPa、800MPa和1000MPa下的稳态蠕变率分别为6.1513×10-6，8.8901×10-6，1.7885×10-5。

1.1000 MPa试验值　2.1000 MPa拟合曲线3.800 MPa试验值　4.800 MPa拟合曲线5.600 MPa试验值　6.600 MPa拟合曲线图5　稳态阶段蠕变曲线及其线性拟合图

图6所示为模拟点与试验点的对比。

图6　模拟点与试验点比较

3　材料蠕变与挤压筒过盈量变化之间的关系研究

材料蠕变导致挤压筒各层筒之间的过盈量减小，产生的装配压应力不足以抵消摩擦等产生的轴向剪切力，使得挤压筒内衬在挤压过程中脱出，严重影响挤压机的正常运行。经分析发现，蠕变对挤压筒各衬间过盈量的影响机理为：挤压筒各层衬在长时间高温高压作用下发生蠕变，出现不可恢复的膨胀变形，而在交界面处由于应力不连续造成变形程度不一，投影到径向便表现为衬间过盈量发生变化，在过盈量减小到一定程度后，就可能因为端面冲击等因素导致内筒脱出等状况发生。本研究将对挤压筒内由蠕变造成的变形进行分析，求得过盈量由设计值变形至临界值所需循环次数或时间作为挤压筒蠕变损坏的寿命值。为简化分析，作如下假设：

(1)挤压终了后，弹性变形完全恢复，而由蠕变造成非弹性应变仍然存在并会随着挤压的不断进行而累加；

(2)蠕变造成的变形与过盈量的改变对下一次挤压过程中挤压筒的应力计算与演变不会造成影响；

(3)假定整个挤压过程中挤压筒温度恒定，忽略温度波动对蠕变量和蠕变变形的影响。

在此前提下，仅需计算单次挤压过程中的挤压筒应力场随时间的变化规律，再按照Norton公式计算各点蠕变率，进而求得蠕变变形即可。挤压筒内应力场演变与Norton公式参数值已求得，确定微观应变与宏观位移之间的关系便显得至关重要。由蠕变率推导求得过盈量改变的过程如下：

(1)选择Norton公式计算各点蠕变率。考虑到挤压筒应力分布随位置、时间而变化，改写式(6)为

(7)

(8)

式中，ttotal为挤压过程总时间。

由式(8)计算得到的蠕变应变为位置(z,r)的函数。

(9)

则

Δl=εθc(2πr)

式中，Δl为周长伸长量。

图7　应变与位移之间关系示意图

将上述切向位移投影到径向，得到对应的半径变化量Δr为

(10)

第i层筒外径变化量Δri,out为

Δri,out=ri,outεθc|r=ri,out

其中，εθc|r=ri,out为第i层筒外径处的蠕变量。第i+1层筒内径变化量Δri+1,in为

Δri+1,in=ri+1,inεθc|r=ri+1,in

(11)

其中，εθc|r=ri+1,in为第i+1层筒内径处的蠕变量。由于交界面处的切向应力不连续，求解出的蠕变速率和蠕变应变有所差别，造成径向变形不一，使得过盈量减小，减小量ΔΔ为

ΔΔ=|Δri,out-Δri+1,in|

(12)

由式(12)计算得到的过盈减小量ΔΔ仅与轴向坐标z有关。N次挤压后(i,i+1)层筒间过盈量变为

Δ′=Δini-NΔΔ

式中，Δini为(i,i+1)层筒间的初始过盈量；Δ′为N次挤压后的过盈量。

4　实例分析

以60 MN挤压机上使用的三层组合挤压筒为研究对象来进行分析。假定三层衬的弹性模量和泊松比相等，即Ei=E=183 GPa，μi=μ=0.3，内载荷p0=500 MPa，z0=100 mm，zL=700 mm，过渡段l=50 mm，挤压速度v=5 mm/s。挤压筒半径及过盈量尺寸如表2所示。Norton公式参数由MATLAB编程计算得B=8.763×10-13，n=2.433。计算挤压N=1000次后的内筒、中筒的过盈量Δ12和中筒、外筒间的过盈量Δ23。

表2　三层挤压筒各层筒半径及过盈量　mm

1.外筒内侧　2.中筒内侧　3.中筒外侧　4.内筒外侧图8　挤压1000次后各层筒交界面处蠕变量分布规律

经过1000次挤压后，得到挤压筒各层筒交界面处的蠕变量分布规律，如图8所示。分析内筒外侧和中筒内侧的交界面与中筒外侧和外筒内侧的交界面处的蠕变规律，可知在交界面处相邻筒之间的蠕变应变有差别，这与交界面处的切向应力不连续相符。此外，还获得了沿挤压方向相同纵坐标处各筒横截面蠕变量随径向的变化曲线，如图9所示。从图9中也能观察到交界面处的蠕变量的不连续性，并可推知在外筒内侧z=700 mm处的蠕变量最大。

图9　挤压1000次后同一z坐标处沿径向蠕变曲线对比

由于各层筒之间交界面处蠕变应变有所差别，造成径向变形不一，故而使得过盈量减小。计算得到挤压1000次后挤压筒内筒和中筒过盈量Δ12和中筒和外筒间过盈量Δ23如表3所示，其前后变化对比如图10所示。

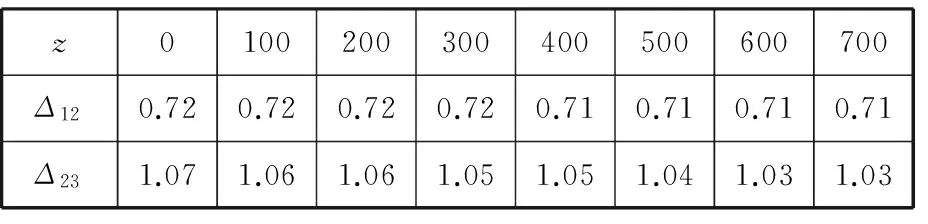
表3　1000次挤压后内中筒、中外筒过盈量　mm

1.中筒、外筒原始过盈量　2.中筒、外筒挤压后过盈量3.内筒、中筒原始过盈量　4.内筒、中筒挤压后过盈量图10　挤压1000次后过盈量变化曲线

5　结论

(1)本文在传统Lamé公式分析挤压筒应力应变的基础上，引入利用位移协调条件求解挤压筒应力应变分布的DDM方法，可更有效地求解多层筒间界面力。

(2)将边界条件简化为随时间不断前移的斜坡载荷，并以分段函数形式加以表示，在此基础上推导了挤压筒在一个挤压周期内的应力场演变模型，获得了挤压筒任意位置点应力随时间的变化状况。

(3)通过试验确定了挤压筒材料H13热作模具钢的Norton模型参数，分析了蠕变变形对多层筒过盈量的影响规律，获得了计算过盈量随挤压次数变化的计算流程。

[1]王家旺.挤压筒的损坏原因及其补救预防措施[J] .轻合金加工技术，2014，42(3)：41-43.

WangJiawang.CausesofContainerFailureandRemedy&PreventionMeasures[J] .LightAlloyFabricationTechnology，2014，42(3)：41-43.

[2]SommitschC，SievertR，WlanisT，etal.ModellingofCreep-fatigueinContainersduringAluminiumandCopperExtrusion[J].ComputationalMaterialsScience，2007，39(1)：55-64.

[3]SommitschC，SievertR，WlanisT，etal.LifetimeEvaluationofTwoDifferentHotWorkToolSteelsinAluminiumExtrusion[J].ComputationalMaterialsScience，2008，43(1)：82-91.

[4]KrumphalsF，WlanisT，SievertR，etal.DamageAnalysisofExtrusionToolsMadefromtheAusteniticHotWorkToolSteelBohlerW750 [J].ComputationalMaterialsScience，2011，50 (4)：1250-1255.

[5]KrumphalsF，ReggianiB，DonatiL，etal.DeformationBehaviourofaFerriticHot-workToolSteelwithRespecttotheMicrostructure[J].ComputationalMaterialsScience，2012，52(1)：40-45.

[6]LaueK,StengerH.Extrusion:Processes,Machinery,Tooling[M].Ohio：AmericanSocietyforMetals， 1981.

[7]敖文刚，王歆.运用统一强度理论分析预应力组合圆筒分层半径和过盈量[J] .重庆工商大学学报(自然科学版)，2011，28(3)：284-288.

AoWengang，WangXin.ApplicationofUnifiedStrengthTheorytoAnalysisofSeparateRadiusandShrinkrangeofPrestressedCombinationTubes[J].JournalofChongqingTechnologyandBusinessUniversity(NaturalScienceEdition)，2011，28(3)：284-288.

[8]赵云路，刘静安，陈卫民.圆挤压筒改装成扁挤压筒的试验研究——80MN挤压机670mm×270mm×1600mm扁挤压筒的设计与制造[J].轻合金加工技术，2001，29(6) ：29-35.

ZhaoYunlu，LiuJing’an，ZhaoWeimin.TrailStudyonRefittingRoundContainerintoFlatOneinExtrusionPress—DesignandManufactureof670mm×270mm×1600mmFlatContainerin80MNPress[J].LightAlloyFabricationTechnology，2001，29(6) ：29-35.

[9]谢水生，贺金宇，徐盈辉，等.扁挤压筒结构参数优化及分析研究[J].塑性工程学报，2001，8(4)：26-29.

XieShuisheng，HeJinyu，XuYinghui，etal.AnalyzetheInfluenceofStructureParameterofMulti-layerFlatContainerbyFEM[J].JournalofPlasticityEngineering，2001，8(4)：26-29.

[10]李燕，刘全坤，王匀，等.三层预紧扁挤压筒变形及应力分布的数值模拟[J].中国机械工程，2003，14(12)：1074-1076.

LiYan，LiuQuankun，WangYun，etal.NumericalSimulationonDeformationandStressDistributionofFlatExtrudedContainer[J].ChinaMechanicalEngineering，2003，14(12)：1074-1076.

[11]刘全坤，王匀.基于Lagrange插值的变过盈量对扁挤压筒变形和强度分析[J].中国机械工程，2004，15(2)：168-170.

LiuQuankun，WangJun.AnalysisonDeformationandStrengthofFlatContainerunderChangeableShrink-fittingRangeBasedonPolynomialInterpolating[J].ChinaMechanicalEngineering，2004，15(2)：168-170.

[12]冯秋红，刘全坤，胡龙飞.基于多目标优化的扁挤压筒结构设计[J].中国机械工程，2006，17(17)：1850-1853.

FengQiuhong，LiuQuankun，HuLongfei.StructuralDesignofFlatExtrusionContainerBasedonMulti-objectiveOptimization[J].ChinaMechanicalEngineering，2006，17(17)：1850-1853.

[13]LuoYuanxin，XiongYikun，WangYongqing，etal.ANewModelforPredictingofStressesontheCompoundExtrusionContainer[J].WSEASTransactionsonAppliedandTheoreticalMechanics，2014，9：229-237.

[14]王玲玲.铝挤压机挤压筒的失效分析[J].锻压技术，2013，38(1)：56-60.

WangLingling.FailureAnalysisofExtrusionCylinderforAlumiumExtrusionPress[J].Forging&StampingTechnology，2013，38(1)：56-60.

[15]曹起骧，肖颖，叶绍英.用光电扫描云纹法研究挤压筒壁上的接触应力分布[J].模具技术，1986(2)：1-9.

CaoQixiang，XiaoYing，YeShaoying.StudyontheCntactStressDistributionontheWalloftheExtrusionCylinderbythePhotoelectricScanningMoireMethod[J].DieandMouldTechnology，1986(2)：1-9.

(编辑卢湘帆)

CreepEffectsonInterferencesofExtrusionContainerwithConsiderationofWorkingConditions

LiYihongLuoYuanxinMaLingSongZongtaoWangYongqin

ChongqingUniversity,Chongqing,400030

Ananalyticalmethod,alsocalleddirectiondisplacementmethod(DDM),wasproposedbasedontheLaméequationtopredictthestress/strainevolutioninextrusioncontainer.Then,theexperimentsforevaluatingthecreepeffectsofH13steelatthetemperatureof500℃wereconducted,andthecreepbehaviorwasmodelledbyusingNorton’slaw.Finally,acasestudywasinvestigatedtoanalyzetherelationshipbetweenmaterialcreepeffectsandinterferences.Itisfoundthatthecreepstrainofeachlayerintheinterfaceisdifferent,causedtheradialdeformationisdifferent,thustheinterferencesarereduced.

extrusioncontainer;interference;creepeffect;H13steel

2015-10-29

国家自然科学基金资助项目(51405044，51345013)

O344.6；TG111.8；TG113.2

10.3969/j.issn.1004-132X.2016.16.019

李一红，女，1991年生。重庆大学机械工程学院硕士研究生。主要研究方向为机械设计及理论。罗远新(通信作者)，男，1981年生。重庆大学机械工程学院副教授、博士。马玲，女，1989年生。重庆大学机械工程学院博士研究生。宋宗焘，男，1989年生。重庆大学机械工程学院硕士研究生。王勇勤，男，1961年生。重庆大学机械工程学院教授、博士研究生导师。