双相激波摆杆活齿传动压力角分析

宜亚丽　邵　苍　金贺荣

燕山大学，秦皇岛，066004



双相激波摆杆活齿传动压力角分析

宜亚丽邵苍金贺荣

燕山大学，秦皇岛，066004

将压力角作为传力特性评价指标，用以指导双相激波摆杆活齿传动设计参数的选取。基于活齿啮合理论，运用复数矢量法建立齿形方程，以两类典型传动为研究对象，推导了压力角解析式，分析了各压力角的变化规律，确定了压力角与摆幅系数、中心轮齿数、基圆半径、摆杆长度以及中心距的关系。运用正交试验法，选取四因素三水平试验表进行方案设计，获得了各设计参数对压力角的影响权重。

双相激波；摆杆活齿传动；压力角；正交试验

0　引言

双相激波活齿传动的激波凸轮是几何轴对称的[1-2]，在传动过程中易实现活齿啮合副的静态、动态受力自平衡，工程应用前景广阔。目前，国内外学者对双相激波活齿传动的研究主要集中在传动原理[3]、齿形设计[4]、接触应力与结构设计[5]等方面。作为度量机构传动力性能优劣的重要指标，压力角在机构受力分析、效率计算和优化设计中都是一个非常重要的参数[6-7]，研究压力角变化规律及其影响因素是完善其设计理论的重要基础。

双相激波摆杆活齿啮合副为全滚动接触，传动效率高，传动过程为多齿啮合[8]，本质为正反凸轮机构串联，对其压力角的分析和评判较一般传动机构复杂。本文选用运动平缓无冲击的余弦类函数描述摆杆的运动规律，运用复数矢量法反求激波凸轮和中心轮的齿形方程，推导出活齿啮合副的压力角解析式，分析压力角的变化规律及其影响因素，采用正交试验法得到各因素对压力角的影响权重。

1　齿形方程建立

双相激波摆杆活齿传动机构由激波凸轮、中心轮、活齿架、摆杆和活齿组成，活齿和摆杆通过销轴组成转动副，摆杆和活齿架通过销轴组成转动副，原理如图1所示，图中，只有激波凸轮、中心轮、活齿架三个互相独立的元件能与外界连接，称之为基本元件。

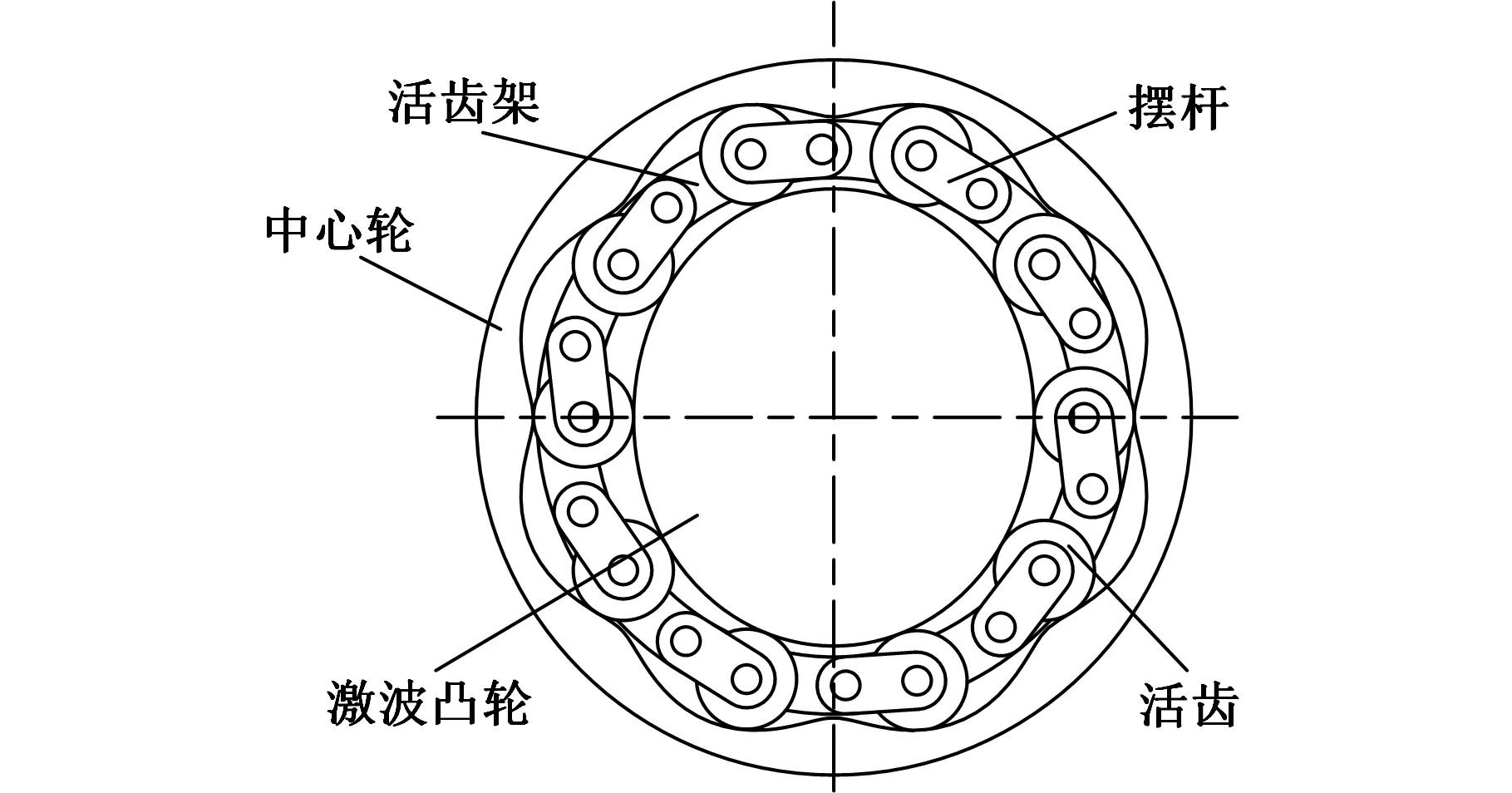
图1　双相激波摆杆活齿传动原理简图

双相激波摆杆活齿传动类属于行星传动，具有2个自由度，因此需要固定某一基本元件，将其转变为单自由度系统。中心轮固定，激波凸轮输入、活齿架输出的传动，记为Ⅰ类传动；活齿架固定，激波凸轮输入、中心轮输出的传动，记为Ⅱ类传动。

图2为激波凸轮生成原理图，RH为激波凸轮齿廓矢量，r0为激波凸轮基圆半径，l为摆杆长度，c为激波凸轮转动中心与摆杆摆动中心的距离,αH为齿形发生角，θ为摆杆和中心距的夹角，βH为摆杆与x轴的夹角，则激波凸轮理论齿廓方程为

RH=cexp(jαH)+lexp(jβH)

(1)

βH=αH+π-θθ=θ0+S

S=A[1-cos(ZHαH)]

式中，θ0为初始摆杆位置与中心距的夹角，由初始结构参数确定；S为摆杆运动函数；A为摆幅系数；ZH为激波凸轮波数。

图2　激波凸轮齿形生成原理图

如图3所示，当激波器转过α′角时，活齿架转过φ角，传动比可表示为

图3　中心轮廓线生成原理图

中心轮齿廓方程可看作激波器相应啮合位置旋转一定的角度得到，RK为中心轮齿廓矢量，考虑相位差中心轮的理论齿廓方程可表示为

(2)

2　机构压力角解析

作为活齿传动的重要动力参数，压力角直接影响传动效率及传力特性。压力角过大，将使传动零件上的载荷增加，传动效率下降。双相激波摆杆活齿传动由1组包含2个滑滚高副和1个转动副的活齿啮合副并联组成(活齿与摆杆间的转动副为局部自由度)。不考虑构件的惯性力和运动副的摩擦力，机构运动时从动件所受驱动力的作用线与该力作用点处运动的绝对速度方向线之间所夹的锐角称为压力角[9]。对于双相激波摆杆活齿传动，激波凸轮和中心轮的理论廓线决定了各构件的运动和受力状况，压力角可由各啮合位置理论廓线的切线和极径间关系得到[10-11]。

切线和极径夹角u可由下式得到：

(3)

将式(1)、式(2)代入式(3)可得到激波凸轮和中心轮理论齿形曲线各点极径和切线的夹角。

双相激波摆杆活齿机构中，激波凸轮为输入基本元件，中心轮和活齿架以排列组合方式分别为输入或输出基本元件时，运动副之间的压力角各不相同。

2.1Ⅰ类传动的压力角

以一个活齿为研究对象，其在推程过程中的压力角如图4 所示。激波凸轮和活齿间的压力角α1为激波凸轮对活齿法向作用力与活齿运动方向所夹锐角。活齿的绝对速度方向为激波凸轮理论廓线和中心轮理论廓线交点处的中心轮理论廓线的切线方向，受力方向为激波凸轮理论廓线的法线方向，取激波凸轮法线、中心轮切线和向径的方向夹角分别为β1和β2，则α1可表示为

α1=|β2-β1+π/2|

(4)

活齿和活齿架间的压力角α2可表示为

α2=|π/2-θ|

(5)

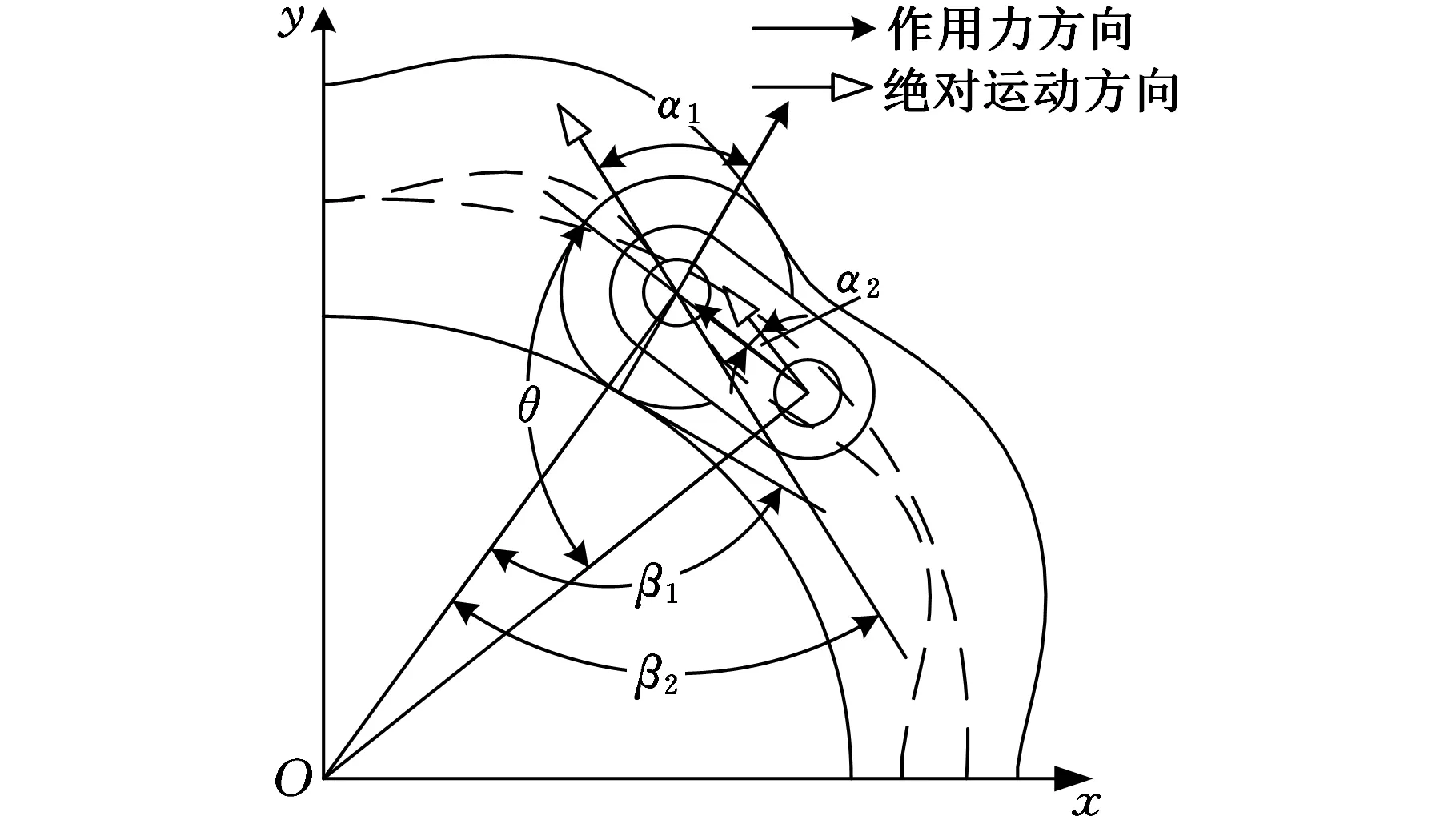
图4　Ⅰ类传动的压力角解析

根据某连续输送机械用减速器设计要求，取定双相激波摆杆活齿传动的基本参数如下：基圆半径r0=95mm，中心距c=100mm，摆杆长度l=20mm，中心轮齿数ZK=8，摆幅系数A=0.25。双相激波凸轮活齿传动一个推程的啮合周期为90°，压力角α1和α2的变化如图5所示，ψ为激波凸轮相对活齿架转角, ψ1、ψ2分别为α1和α2取最小值时激波凸轮相对活齿架的转角。

图5　Ⅰ类传动的压力角变化曲线

2.2Ⅱ类传动的压力角

如图6所示，同样分析一个活齿啮合阶段，即激波凸轮相对中心轮转动90°的压力角变化情况，γ为向径和摆杆的夹角，γ1、γ2分别为啮合点处激波凸轮和中心轮理论廓线的切线与向径的夹角。

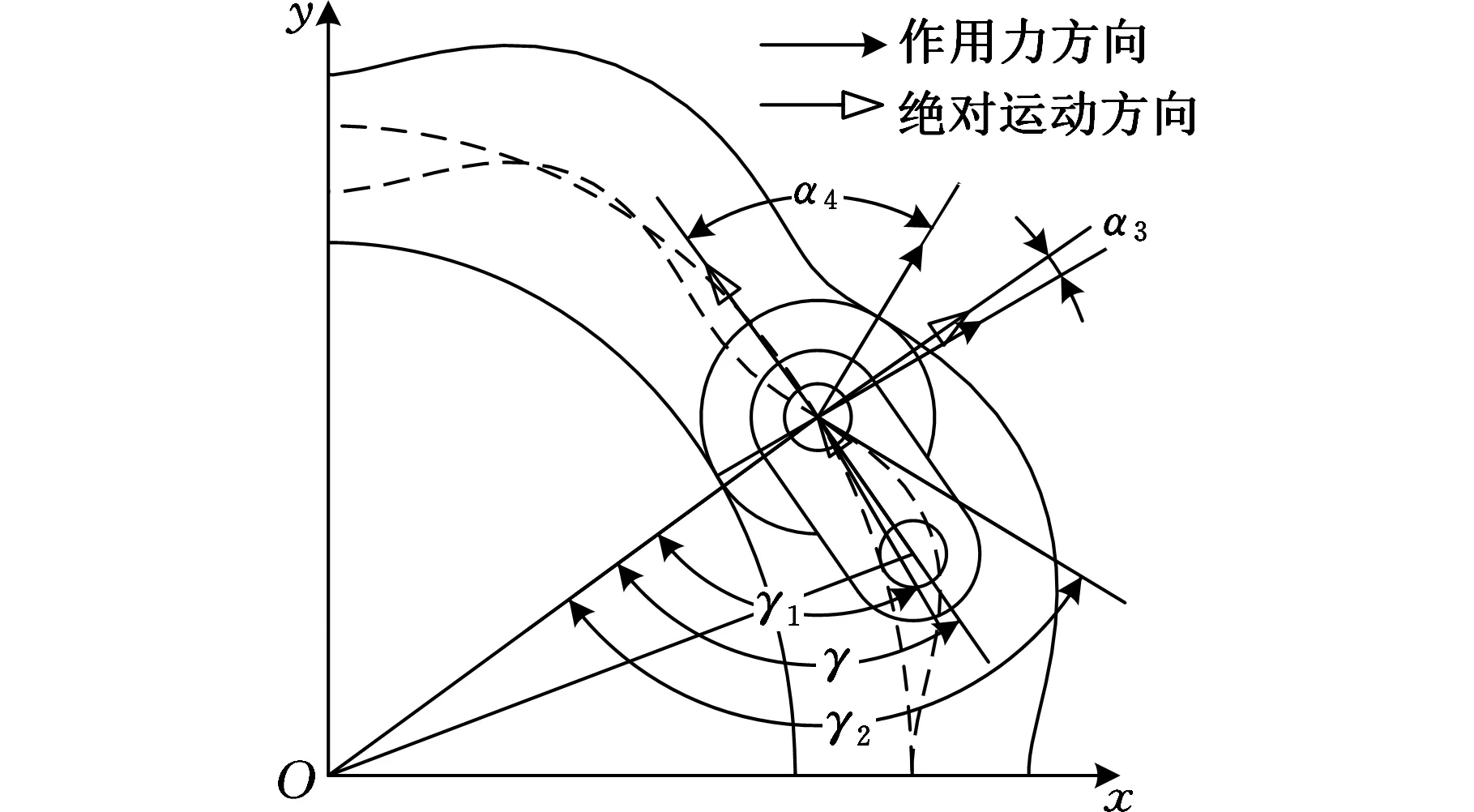
图6　Ⅱ类传动的压力角解析

激波凸轮和活齿间的压力角可表示为γ1、γ2之差，即

α3=|γ1-γ2|

(6)

中心轮在啮合点处运动方向和向径垂直，则活齿和中心轮的压力角可表示为

α4=|π-γ2|

(7)

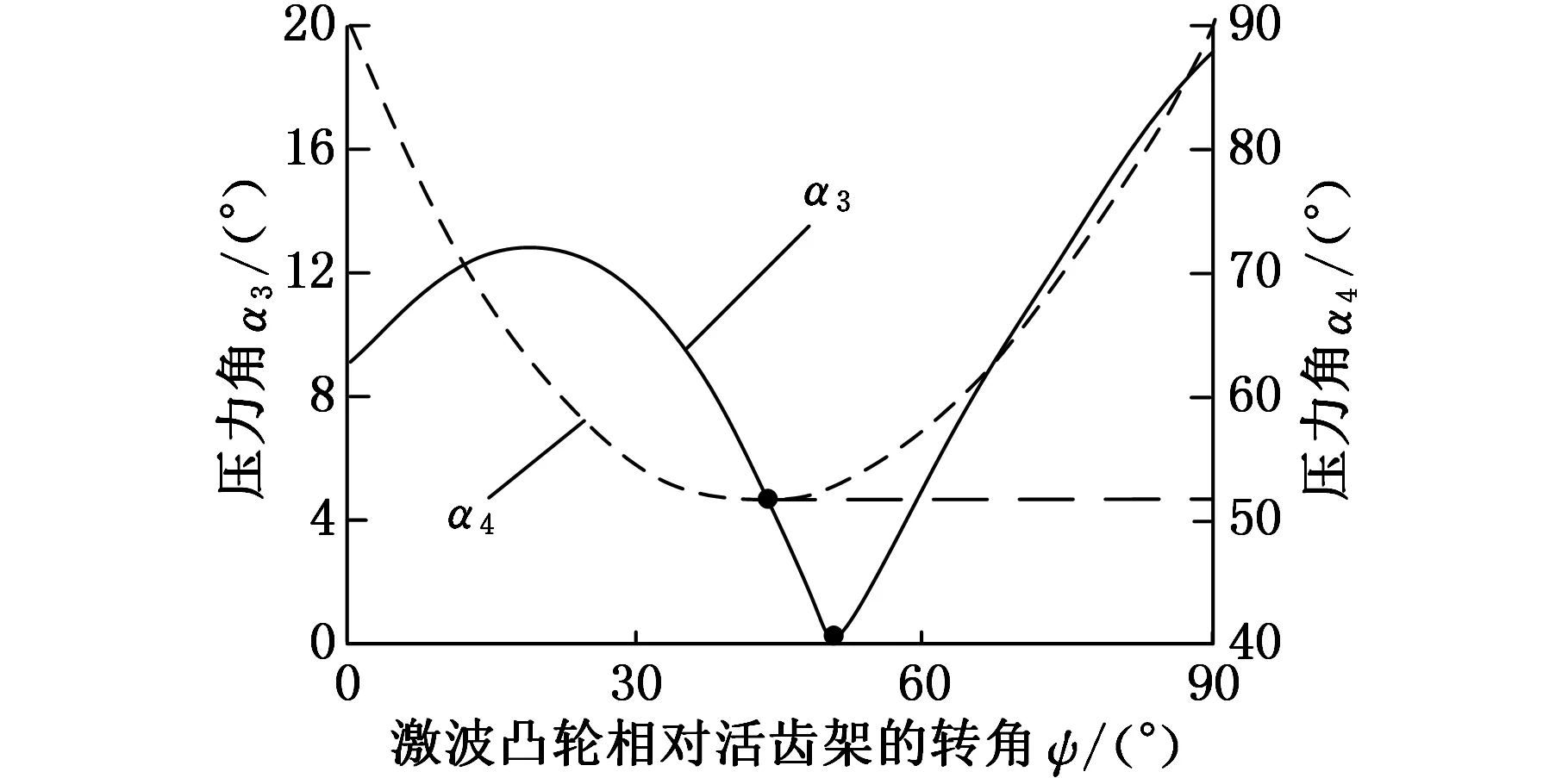
图7　Ⅱ类传动的压力角变化曲线

保持传动参数不变，利用式(6)、式(7)得到压力角α3和α4的变化曲线，如图7所示。ψ3、ψ4分别为α3和α4取最小值时激波凸轮相对活齿架的转角。

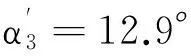
2.3机构压力角的影响因素

通过对机构压力角的解析，可知摆幅系数A、中心轮齿数ZK、基圆半径r0、摆杆长度l和中心距c共同影响机构的压力角。设计机构时，可根据传动类型，通过合理选择参数使机构的压力角达到理想水平。由图5、图7可知，压力角α1、α4的最大值均为90°，压力角α2、α3的最小值均为0°。活齿机构为并联啮合副，同一时刻有多个活齿啮合，可满足传动需求。本文分析各传动参数分别对压力角α1、α4的最小值，压力角α2、α3的最大值的影响。压力角不随机构中各构件尺寸等比例缩放而改变[12]，定义基圆半径系数r0/c和摆杆长度系数l/c，将中心距c对压力角的影响转化为基圆半径系数r0/c和摆杆长度系数l/c对压力角的影响，因此压力角的变化情况最终取决于基圆半径系数r0/c、摆杆长度系数l/c、摆幅系数A以及中心轮齿数ZK。分别得到α1min、α4min、α2max和α3max随各影响因素变化的关系。

图8　摆幅系数对各压力角的影响

中心轮齿数对各压力角的影响如图9所示，随着中心轮齿数的增大，α1min、α4min减小；α2max只与初始位置以及摆动幅度有关，和中心轮齿数无关；α3max为激波凸轮和活齿啮合副对应压力角，改变中心轮齿数，激波凸轮和活齿的啮合状态不发生变化。因而α2max、α3max不受中心轮齿数的影响。

图9　中心轮齿数对各压力角的影响

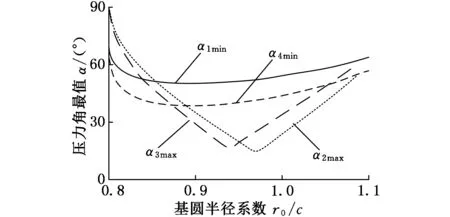
图10　基圆半径系数对各压力角的影响

图11　摆杆长度系数对各压力角的影响

2.4正交试验

由于影响压力角变化的各因素相互独立，可根据压力角受各因素影响的变化趋势选取四因素三水平的正交表[13-14]L9(34)进行方案设计，各水平及因素选取如表1所示。

表1　因素水平选择表

进行9次试验，得到各压力角的试验结果，如表2所示。

表2　试验结果

为得到各影响因素的权重，将表2中同一因素同一水平下各压力角的最值相加，绘制变化曲线，如图12所示。

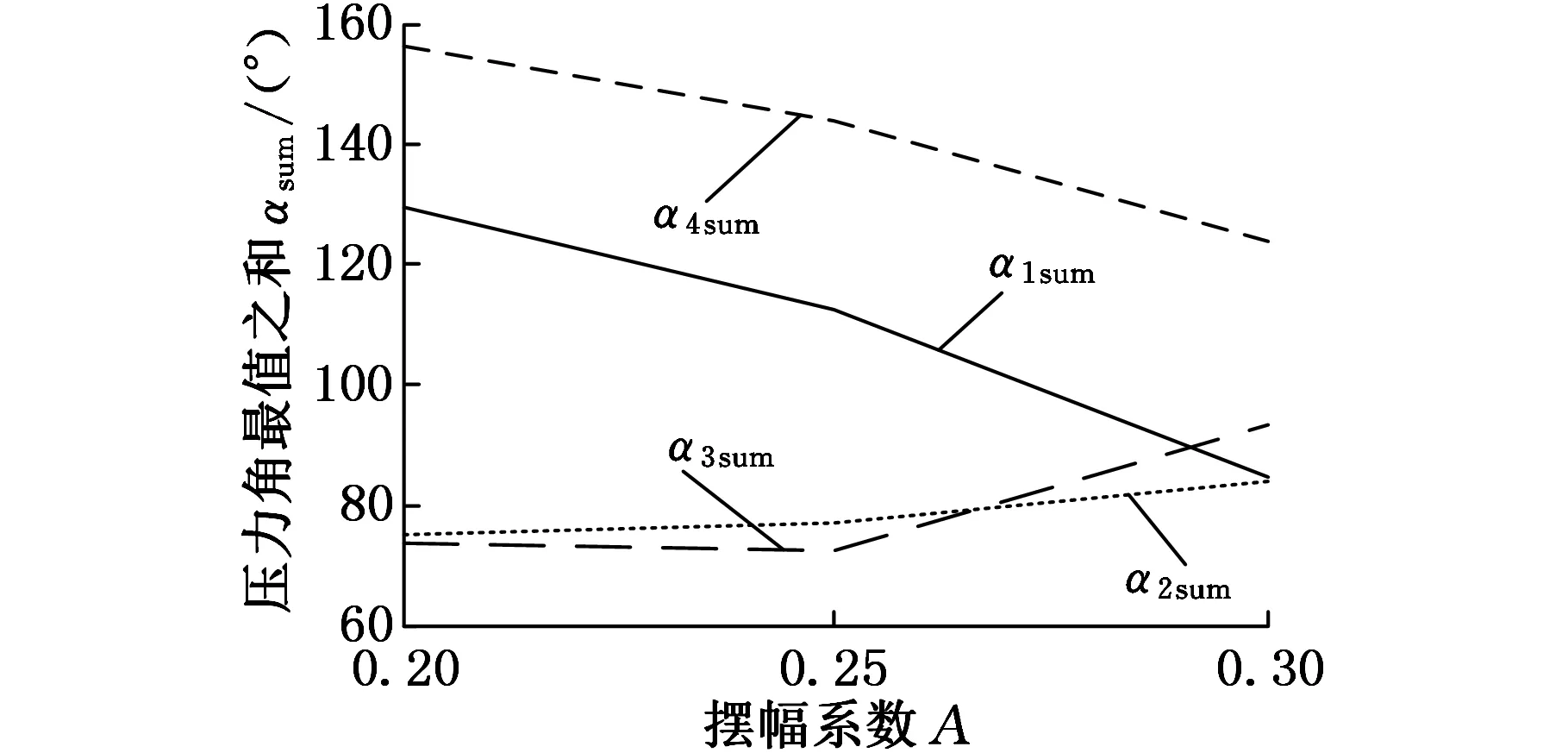
(a)摆幅系数的影响

(b)中心轮齿数的影响

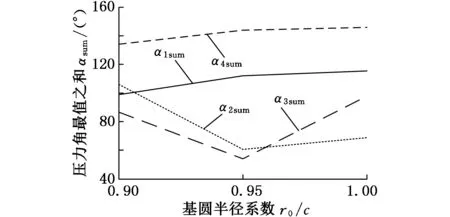
(c)基圆半径系数的影响

(d)摆杆长度系数的影响图12　各影响因素与压力角最值之和α1sum～α4sum的关系

基于上述分析可确定各压力角在各因素水平上的极差，极差分析结果如图13所示；对极差大小进行排序即可得到各因素对各压力角影响灵敏度排序，如表3所示。分析表明，摆幅系数A、中心轮齿数ZK和基圆半径系数r0/c对压力角的影响较大，摆杆长度系数l/c对压力角影响较小。

图13　各因素对压力角影响灵敏度分析

压力角1234α1AZKl/cr0/cα2r0/cl/cZKAα3r0/cZKAl/cα4ZKAl/cr0/c

3　结论

(1) 两类传动型式下，各压力角均随啮合位置的变化而变化。压力角最大值均出现在活齿进入啮合或退出啮合的位置，压力角最小值一般出现在啮合过程的中点附近。

(2)基圆半径系数r0/c、摆杆长度系数l/c、摆幅系数A以及中心轮齿数ZK对各压力角α1min、α4min、α2max和α3max均有不同程度的影响，且影响呈现不同规律。

(3)运用正交试验法，选用四因素三水平的正交试验表，设计并进行了模拟试验，得到了影响各个压力角因素的主次关系，其中，摆幅系数A、中心轮齿数ZK和基圆半径系数r0/c对压力角的影响较大，摆杆长度系数l/c对压力角影响较小。

[1]曲继方,安子军,曲志刚. 机构创新原理[M].北京:科学出版社,2001.

[2]董新蕊,李剑锋,王新华,等. 凸轮激波复式活齿传动的结构及齿形分析[J]. 中国机械工程, 2006,17(16): 1661-1665.

Dong Xinrui, Li Jianfeng, Wang Xinhua, et al. Structural and Tooth Profile Analysis on Cam Profile Compound Teeth Transmission[J]. China Mechanical Engineering, 2006,17(16):1661-1665.

[3]Anghel S, Anghel C V. Contributions to Kinetostatic Calculus of a New Cycloidal Swing Link Speed Reducer[C]//The 8th Symposium on Mechanisms and Mechanical Transmission with International Participation. Timisoara, 2000:19-22.

[4]赵纯可,梁尚明,张杰. 二齿差摆杆活齿传动的齿形分析与仿真[J]. 四川大学学报(工程科学版),2015,47(增刊1):151-157.

Zhao Chunke, Liang Shangming, Zhang Jie. Tooth Profile Analysis and Simulation of the Two-tooth Difference Swing-rod Movable Teeth Transmission[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(S1) :151-157.

[5]王素,白鑫,陈仕贤,等. 离散齿谐波传动啮合力及接触应力分析[J].重庆大学学报，2013，36 (1)：35-42.

Wang Su, Bai Xin, Chen Shixian, et al. Research on Analysis of Force and Contacting Stress for the Discrete Teeth Harmonic Drives[J]. Journal of Chongqing University，2013，36 (1)：35-42.

[6]刘大伟,任廷志,章裕琳. 非匀速活齿机构的传动原理及典型结构[J]. 机械工程学报,2014,50(1):47-54.

Liu Dawei, Ren Tingzhi, Zhang Yulin. Transmission Theory and Typical Structure of Nonuniform Mechanism with Movable Teeth[J]. Journal of Mechanical Engineering, 2014, 50(1):47-54.

[7]水上正巳,寺田英嗣.可動ピン入力形トロコイド歯車減速機に関する研究(第2報)-圧力角解析[J]. 精密工学会誌,2010,76(6):663-667.

[8]宜亚丽,安子军,曾达幸. 偏心式摆动活齿啮合副自锁机理研究[J].中国机械工程,2012,23(4):454-457.

Yi Yali，An Zijun，Zeng Daxing.Study on Self-locking Mechanism of Meshing Pairs of Eccentric Swing Movable Teeth[J]. China Mechanical Engineering,2012,23(4): 454-457.

[9]Terada H, Masuda T, Yoshida S. Motion Analysis of a Reciprocating Motion Type Ball Reducer[C]//12th IFTOMM World Congress. Besanon, France, 2007: 414-418.

[10]陈文华. 切线极坐标在仪表齿形研究中的应用[J]. 浙江大学学报(自然科学版),1995,29(4):441-447.

Chen Wenhua. Applications of Tangential Polar Coordinates in Instrument Gear Research[J]. Journal of Zhejiang University (Natural Science), 1995, 29 (4): 441-447.

[11]肖望强,李威,韩建友,等. 双压力角非对称齿廓渐开线齿轮的振动分析 [J].中国机械工程,2006,17(6):644-649.

Xiao Wangqiang, Li Wei, Han Jianyou, et al. Vibration Analysis of Involute Gear with Unsymmetric Teeth and Double Pressure Angles [J]. China Mechanical Engineering, 2006,17(6):644-649.

[12]朗内斯J A, 纳耳桑G L.四连杆机构分析图谱[M]. 李学荣,译. 北京:机械工业出版社,1966.

[13]任露泉.试验设计及其优化[M].北京:科学出版社,2009.

[14]刘萍,张轲. 水射流技术回收子午线轮胎的正交试验 [J].中国机械工程,2015,26(14):1964-1968.

Liu Ping, Zhang Ke. Orthogonal Experiments on Recycling Radial Tires Using High Pressure Water Jet Techniques [J]. China Mechanical Engineering, 2015, 26(14): 1964-1968.

(编辑张洋)

PressureAngleAnalysisofaDoubleGeneratingWaveSwingRodMovableToothDrive

YiYaliShaoCangJinHerong

YanshanUniversity,Qinhuangdao,Hebei,066004

Thepressureanglewasusedastheevaluationindexofforcetransmissioncharacteristicstoguidethedesignparametersofdoublegeneratingwaveswingrodmovabletoothdrive.Atoothprofileequationwasestablishedbycomplexvectormethodbasedonthemeshingtheoryofmovabletoothdrive.Takingtwotypicaltransmissiontypesastheresearchobjects,thecalculationformulaeofpressureanglewerededuced.Thechanginglawsofeachpressureanglewereanalyzedtoascertaininfluencesofoscillationamplitudecoefficient,teethnumberofcentralwheel,radiusofbasecircle,lengthofswingrodandcenterdistanceonpressureangles.Byemployingtheorthogonalexperiment,theschemedesignwascarriedoutbasedonexperimentaltablewith4factorsand3levelstoobtaintheinfluenceweightsofeachdesignparameteronpressureangle.

doublegeneratingwave;swingrodmovabletoothdrive;pressureangle;orthogonalexperiment

2015-06-05

国家自然科学基金资助项目(51275440)；河北省高等学校自然科学研究青年基金资助项目(QN2016095)

TH132.41

10.3969/j.issn.1004-132X.2016.16.006

宜亚丽，女，1976年生。燕山大学机械工程学院副教授、博士。主要研究方向为新型机械传动的理论与应用技术。发表论文30余篇。邵苍，男，1990年生。燕山大学机械工程学院硕士研究生。金贺荣，男，1975年生。燕山大学机械工程学院副教授、博士。