基于真应力-应变关系的粗糙表面法向接触模型
2016-09-08王世军王诗义杨慧新赵金娟李淑娟李鹏阳
王世军 杨 超 王诗义 杨慧新 赵金娟 李淑娟 李鹏阳
西安理工大学,西安,710048
基于真应力-应变关系的粗糙表面法向接触模型
王世军杨超王诗义杨慧新赵金娟李淑娟李鹏阳
西安理工大学,西安,710048
提出一种粗糙表面的法向弹塑性接触分析的建模方法。基于微凸体的弹塑性有限元接触模型,分别研究了40Cr、45和Q235三种钢材料的微凸体与刚性平面的法向接触特性。有限元模型中采用三种材料的真应力-应变关系,考察了不同强化特性对微凸体接触性质的影响。建立了微凸体在弹性、弹塑性、塑性变形阶段统一的接触变量变化规律的表达式。在此基础上应用概率统计理论建立粗糙表面法向弹塑性接触模型。所建立的接触模型中微凸体接触变量的变化规律完全基于弹塑性有限元模型的计算结果,无需将微凸体的变形过程区分为不同的变形阶段,避免了接触变量在各阶段采用不同函数表达式带来的连续性和光滑性问题,以及在弹塑性阶段采用插值函数的随意性问题。通过与其他接触模型的计算结果相比较,证明了所提出接触模型的合理性。
粗糙表面;法向;弹塑性变形;接触模型
0 引言
机械零件的接触表面在微观上都是凸凹不平的粗糙表面,零件的接触在微观上都是粗糙表面之间的接触。
文献[1]基于Hertz接触理论提出了粗糙表面的法向弹性接触模型(GW模型)。该模型假设粗糙表面间的接触变形是弹性变形,接触表面由半径相等的弹性微凸体构成,高度分布服从指定的概率分布,各微凸体在接触变形过程中互不影响。GW模型利用Hertz接触理论描述各个微凸体与光滑刚性表面的接触性质,在此基础上,利用概率统计方法获得粗糙表面的接触性质。文献[2]随后对该模型进行了改进,计入了微凸体的塑性变形,并提出对于微凸体高度服从高斯分布的两个粗糙表面,其接触模型可以简化为一个粗糙表面与刚性光滑平面的接触模型(GT模型)。
文献[3]在GW模型和GT模型的基础上,基于微凸体塑性变形的体积守恒原理建立了粗糙表面的弹塑性接触模型(CEB模型)。该模型考虑了微凸体的完全弹性和完全塑性状态,没有考虑两者之间的弹塑性过渡状态,给出的接触载荷与法向接近量的关系在弹性变形与塑性变形的临界点处并不连续,很多基于分形理论的接触分析模型中也采用这种仅考虑弹性阶段和塑性阶段的微凸体变形假定[4-7]。微凸体的接触变形过程中,接触刚度、接触载荷、平均接触压力、接触面积等接触变量连续、单调变化。接触刚度变化的连续性要求接触载荷、平均接触压力、接触面积等接触变量的变化必须光滑,即保持一阶连续,但是CEB模型不满足这种连续性和光滑性要求。
文献[8]针对CEB模型存在的问题,提出了包含弹性、弹塑性和塑性三种变形状态的表面接触模型(ZMC模型),该模型利用插值方法建立微凸体在弹塑性变形阶段接触面积和平均接触压力与法向接近量之间的关系,但该模型还存在微凸体接触压力在不同变形阶段的临界点处不光滑和完全塑性变形临界点不确定等问题。文献[9]进一步对ZMC模型进行改进,采用三次样条函数对接触状态的变化过程进行插值,建立了一种在临界点满足连续性和光滑性要求的法向接触模型。文献[10]采用Hermit多项式对弹塑性变形阶段的接触变化过程进行插值,也获得了一种满足光滑性和连续性条件的接触分析模型。针对文献[9-10]中描述平均接触压力变化的插值函数存在非单调性问题,文献[11]提出采用单调的椭圆曲线描述微凸体弹塑性变形阶段的平均接触压力与法向接近量之间的关系。
上述基于ZMC模型发展起来的包含弹塑性过渡阶段的接触模型,对于弹塑性过渡阶段接触状态的描述都是依赖于选定的插值函数。插值函数的选择只要满足连续性和光滑性要求即可,不同的插值函数在弹塑性过渡阶段的取值会有比较大的差异,不能准确反映接触变量的真实变化规律。文献[12]采用有限元法研究微凸体在接触变形过程中接触变量的变化规律,提出了基于有限元结果的接触分析模型(KE模型)。该模型存在的问题与CEB模型类似,即微凸体接触过程从弹性阶段转变到塑性阶段时接触变量不连续,并且微凸体的材料采用无强化的理想弹塑性模型,这与一般金属材料的性质并不完全一致。文献[13]中基于分形理论的接触模型中微凸体的接触变形规律就采用KE模型中微凸体的接触变量表达式。文献[14]的JG模型在KE模型的基础上进行了改进,满足了接触变量在弹塑性过渡阶段的连续性要求,但是光滑性的要求并没有完全满足,平均接触压力曲线的斜率在弹性阶段的临界点处相差6.1%,并且仍然采用无强化的弹塑性材料模型。文献[15]的KS模型采用试验获得的工程应力-应变关系,该研究中建立了带有强化的弹塑性微凸体有限元接触模型,分析了重载条件下接触变量的变化规律。由于该模型的接触载荷远超过正常机械连接的压力范围,故其接触过程并不表现出弹性阶段和弹塑性过渡阶段的接触性质。
针对上述微凸体接触建模中存在的不足,本文基于材料的真应力-应变关系,采用有限元方法研究微凸体接触变量在弹塑性过渡阶段的变化规律,基于GW模型提出一种改进的粗糙表面法向接触分析模型,避免弹塑性过渡阶段插值函数选择的随意性,同时保证接触变量的光滑和连续。
1 微凸体的接触分析
本文对微凸体的简化仍然采用GW模型的假定,即微凸体的顶部是球形并且具有相同的曲率半径,微凸体的高度随机分布,微凸体的分布密度和曲率半径都是常数,接触变形过程中,假定微凸体之间的变形互不影响,这些假定与CEB模型和ZMC模型一致。
图1是半球形微凸体的轴对称模型。考虑到微凸体的几何和载荷的对称性,在模型的左侧施加水平位移约束。微凸体的底面与基体相连,考虑到基体对微凸体变形的约束特性,将半球底面的位移全部约束。微凸体的半径R=30μm,采用四边形单元,单元总数为20 581个,刚性平面与微凸体之间的接触单元总数为1372个。文献[14]中的接触单元仅100个,而文献[12]中只有225个四边形轴对称单元,接触单元数量更少。

图1 微凸体的有限元模型

图2 三种材料的真应力-应变关系
图2是通过材料拉伸试验获得的三种常用的具有代表性的钢材真应力-应变曲线,本文利用多线性弹塑性各向同性强化模型将这些数据引入有限元接触计算中。图2所示的三种材料除了屈服极限不同外,与理想弹塑性材料相比具有明显的强化特性。与文献[3-14]采用的无强化理想弹塑性材料模型和文献[15]采用的基于工程应力-应变关系的弹塑性材料模型相比,本文的材料模型更符合工程实际。
1.1接触面积与变形量的关系
通过有限元计算获得三种不同材料的微凸体在不同的法向变形量h下的接触面积A后,将计算结果按下式进行量纲一化处理:
(1)
(2)
A1=πRh1
(3)
式中,h*、A*分别为量纲一法向变形量和量纲一接触面积;h1为微凸体由弹性阶段过渡到弹塑性阶段的临界变形量[11];A1为微凸体由弹性阶段过渡到弹塑性阶段的临界接触面积;k为平均接触压力系数[16-17],k=0.4;H为材料硬度,H=2.8σs;σs为材料的屈服极限;μ为泊松比;E为弹性模量。
根据图2的试验数据,Q235的屈服极限σs=240 MPa,45钢的屈服极限σs=360 MPa,40Cr的屈服极限σs=740 MPa。三种材料的泊松比μ=0.3,弹性模量E=207 GPa。
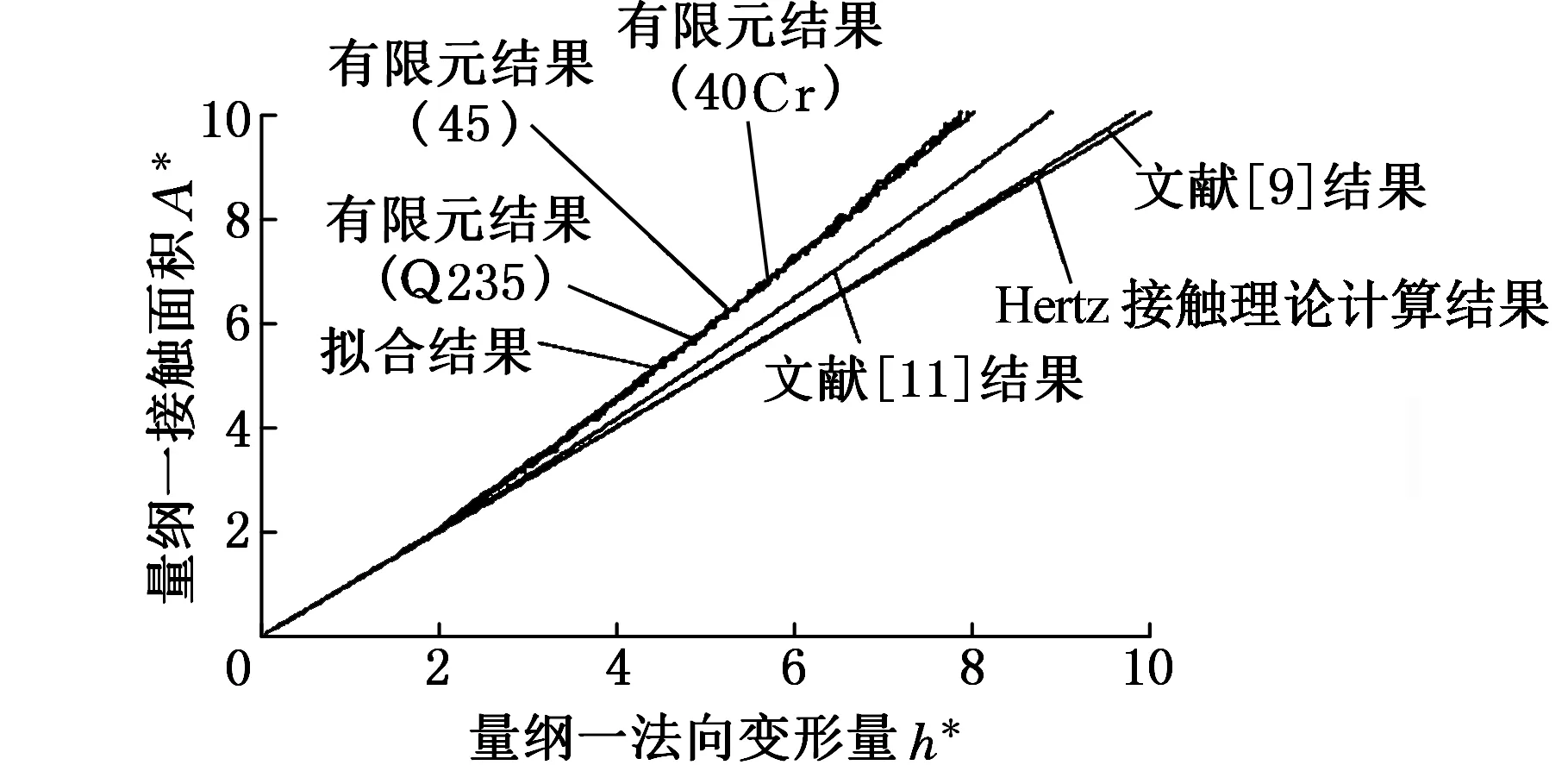
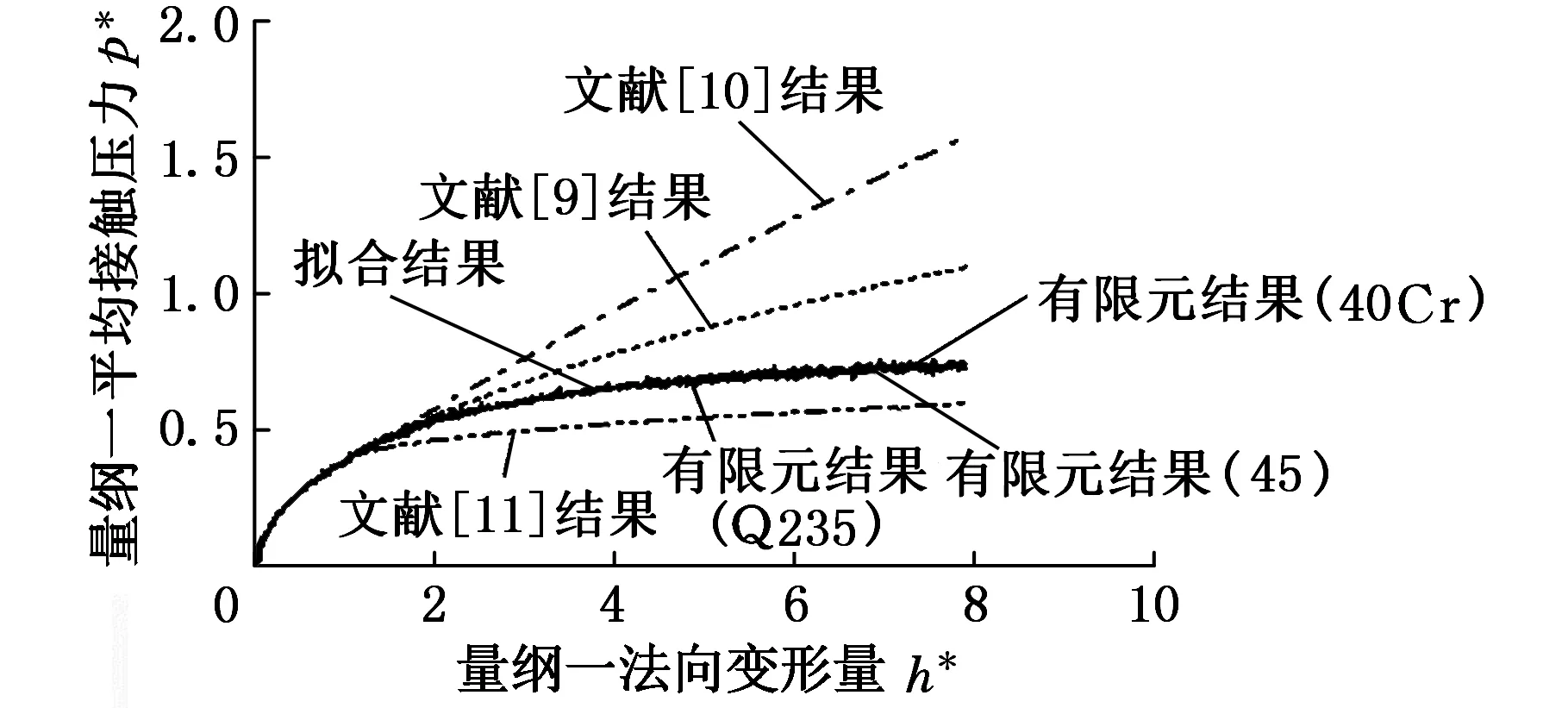
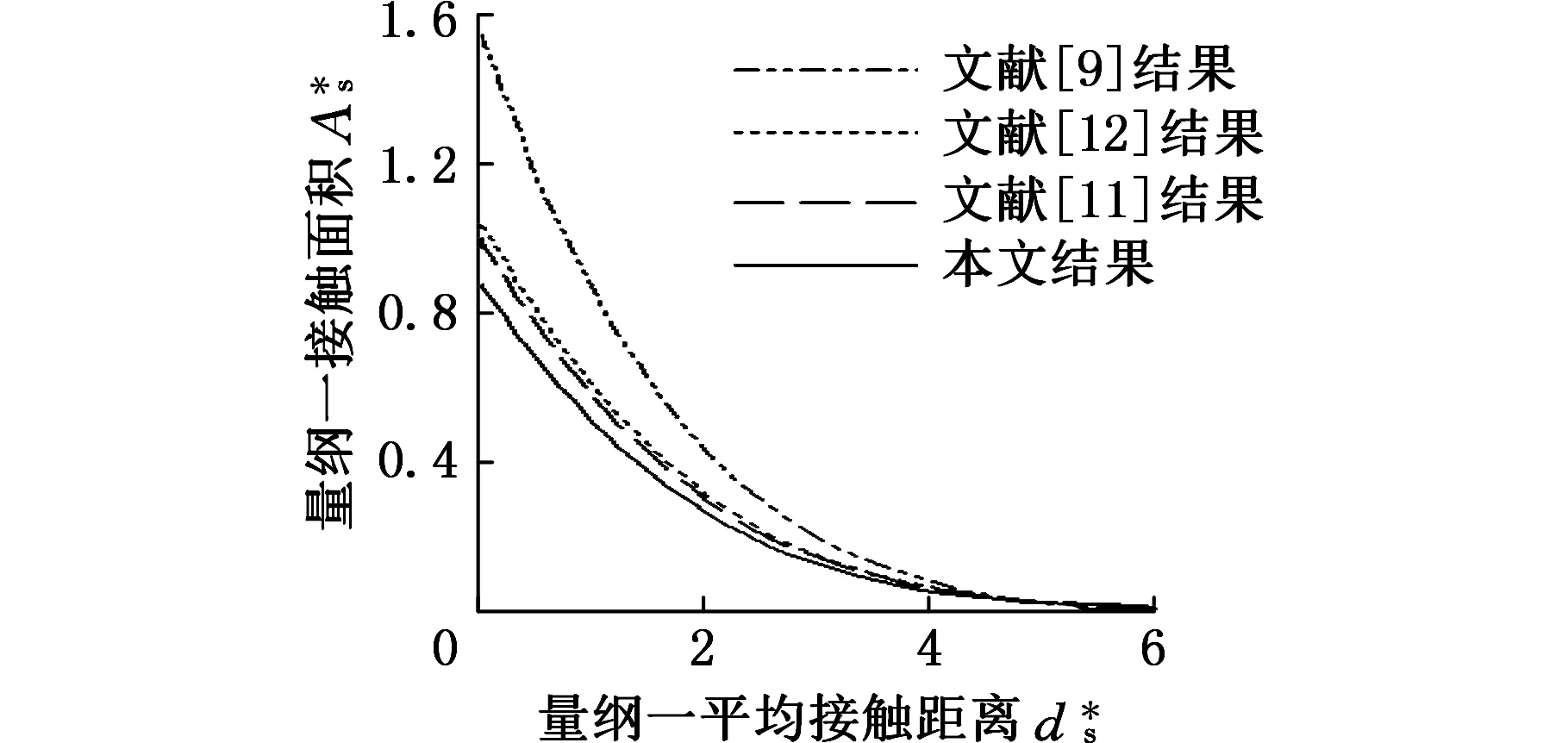
三种材料有限元计算结果量纲一化后的接触面积-法向接触变形关系如图3所示。作为比较,文献[9,11]的曲线也显示在图中。图4是图3在接触变形比较小时的局部放大。两图中三种不同材料的曲线基本重合,表明量纲一化后的面积曲线与材料无关。图4中量纲一的接触变形h*<2时,有限元结果与文献[9,11]中根据Hertz接触理论获得的纯弹性阶段的曲线能够很好吻合,h*>2之后,有限元结果与文献[9,11]以及Hertz接触理论的结果逐渐偏离,这与微凸体中塑性区逐渐变大有关。图3和图4中,文献[11]在弹塑性过渡阶段采用了与文献[10]相同的Hermit插值函数,在这一区间里,文献[10]的结果与文献[11]相同。图3中,在50 图3 量纲一接触面积-法向变形量关系曲线 图4 量纲一接触面积-法向变形量关系曲线(局部放大) 文献[12]由于接触单元数量少,故没有给出h*<1的弹性阶段的接触面积变化的有限元结果,直接采用Hertz接触理论计算接触面积,在1≤h*≤6区间和6 对图3中三种材料的有限元计算结果,本文采用如下两项形式的幂函数来拟合: A*=1.91(h*)1.048+1.262(h*)0.8422 (4) h*<200 该函数拟合了量纲一接触变形从0到200之间的接触面积变化规律,能够连续、光滑地反映微凸体接触面积在弹性阶段、弹塑性阶段和塑性阶段的接触面积变化规律。 1.2接触力与变形量的关系 通过有限元计算获得接触面上的法向载荷F与变形量h,经过量纲一处理后得到图5所示的F*-h*关系曲线,图6是图5法向变形量比较小时的局部放大,其中,量纲一接触力图5和图6中三种不同材料的有限元结果有较好的一致性,文献[9-10]的曲线不单调,与有限元结果差异较大,文献[11]的曲线由于采用单调的插值函数,与有限元结果最为接近。 (5) 图5 量纲一接触力-法向变形量关系曲线 图6 量纲一接触力-法向变形量关系曲线(局部放大) 图6中有限元结果在h*<1时与文献[9-11]中基于Hertz接触理论的曲线能较好地吻合,说明有限元计算结果在这个区间与Hertz理论的结果一致。文献[12]没有给出h*<1时的有限元结果,与接触面积一样,在这一区间接触力直接采用Hertz理论的结果。文献[14]在h*<1.9的区间里也采用Hertz理论的结果。文献[12]在1≤h*≤6和6 本文采用下式拟合图5中量纲一法向力F*与h*之间的关系: F*=1.967(h*)1.182h*<200 (6) 该式统一反映了三种材料的微凸体从弹性、弹塑性到塑性三个阶段的量纲一的载荷-变形规律,满足接触变量的连续性和光滑性要求。 1.3平均接触压力与变形量的关系 通过有限元计算获得微凸体法向接触力和接触面积以后,可以求得法向平均接触压力p与法向变形量h之间的关系。图7是量纲一化后的三种不同材料的平均接触压力p*与法向变形量h*之间的关系,这里平均接触压力p按下式量纲一化: (7) 图7 量纲一平均接触压力-法向变形量关系曲线 为了对比,图7中也给出了文献[9-11]的曲线。图7中文献[11]的曲线与本文的有限元结果较为接近,但是文献[9-10]的曲线在弹塑性过渡阶段都不是单调曲线,有较大的过冲,与本文结果存在较大差异。此外,在h*>110的塑性阶段,文献[9-11]的曲线采用p*=H的水平线,但是本文的有限元结果仍然有逐渐增大的趋势,这与本文计入了材料强化特性有关。文献[12]只给出了弹塑性阶段量纲一化的平均接触压力的有限元结果,在弹性阶段采用Hertz接触理论的结果,塑性阶段的变化规律则与文献[9-11]相同。这样,在不同阶段的临界点处,文献[12]的曲线虽然连续,但是并不光滑。文献[14]在p*>50后的曲线则随材料不同而有明显差异,并且随着变形增大,p*的变化规律也不相同,甚至有逐渐下降的趋势。本文的结果则是三种材料的平均接触压力曲线基本吻合并且在整个接触变形过程中都是单调上升,这与文献[15]在重载条件下的计算结果一致。此外,由于文献[14]中法向力和接触面积在塑性阶段并没有明显地与材料性质相关,因此平均接触压力也不应与材料性质相关,由此本文认为文献[14]给出的在p*>50后接触压力变化规律并不准确。 图8是微凸体量纲一平均接触压力p*在接触变形h*<8时的变化规律。三种材料的接触压力在h*<1时与文献[9-11]采用Hertz接触理论得到的压力曲线一致。文献[14]虽然给出了弹性变形阶段平均接触压力的有限元结果,但是数值上与Hertz理论的结果有明显差异,为此在弹性阶段与文献[12]一样直接采用Hertz接触理论求得的平均接触压力变化规律。这样,在h*=1.9处,文献[14]中的平均接触压力与接触面积和法向力一样存在连续性和光滑性问题。在弹塑性阶段与塑性阶段的临界点处,文献[14]中的平均接触压力也存在同样的问题。 图8 量纲一接触压力-法向变形量关系曲线(局部) 本文采用下述两项的幂函数拟合图7中的有限元结果: p*=1.84(h*)0.3544-1.396(h*)0.3889h*<200 (8) 该函数能够比较好地反映微凸体弹性、弹塑性、塑性各个变形阶段的平均接触压力的变化规律,并能满足单调、连续、光滑的要求。 假定名义接触面积上有N个微凸体,微凸体高度符合高斯分布,则微凸体高度分布的概率密度函数 (9) 式中,σ为微凸体高度分布的方差;z为微凸体的峰高。 粗糙表面间距为d时的真实接触面积 (10) 这里,A=A1A*,h=h1h*,d=z-h。 类似地可以求得间距为d时粗糙表面间的法向接触力和平均接触压力: (11) (12) 由于本文中微凸体接触变量的变化规律完全依据有限元计算结果,无需将接触过程划分为弹性、弹塑性、塑性三个阶段,故反映粗糙表面接触性质的式(10)~式(12)不需要划分为若干个积分区间分别构造积分表达式,形式上比文献[9-12,14]的表达式简洁,并且能够计入材料屈服后的强化特性,满足曲线连续性和光滑性要求。 为了将本文模型与其他相关模型进行对比,采用文献[11]的正则化方法对式(10)~式(12)量纲一化: (13) 曲线 曲线 曲线图9 不同粗糙表面模型的比较 采用有限元法研究弹塑性微凸体的接触性质,在接触区采用高密度的接触单元并计入了材料屈服后的真应力-应变关系,得到的量纲一的微凸体接触变形规律能够比较准确地反映微凸体在弹性、弹塑性和塑性变形过程中的接触性质。虽然量纲一的接触变形规律仅仅是基于三种代表性材料得到的,但是三种不同材料的计算结果具有良好的一致性,这一结果表明,拟合得到的量纲一接触变量表达式对于性能接近的其他钢材也具有一定通用性。对于性能差别较大的材料以及微凸体更大的接触变形,可以采用本文的分析方法得到类似的微凸体的接触变形规律。 基于有限元的微凸体接触特性分析虽然是根据特定半径的微凸体模型进行的,但是经过量纲一处理后得到的接触变量的变化规律具有一般性,与具体的微凸体尺度无关,接触变量表达式的准确性只与有限元模型的准确性和拟合精度有关。微凸体的接触特性是建立粗糙表面分析模型的基础之一,利用本文的研究成果,可以进一步提高粗糙表面接触分析模型的准确性。 只要求连续、光滑和单调并不能唯一确定描述微凸体在弹塑性过渡阶段平均接触压力的变化规律的插值函数。本文在微凸体变形的各阶段采用统一的函数拟合有限元的计算结果,建立统一、连续、光滑的接触变量表达式,能够避免文献[9-11]在弹塑性过渡阶段采用插值函数的随意性带来的理论误差。 [1]GreenwoodJA,WilliamsonJBP.ContactofNominallyFlatSurfaces[J].ProceedingoftheRoyalSocietyA, 1966, 295: 300-319. [2]GreenwoodJA,TrippJH.TheContactofTwoNominallyFlatRoughSurfaces[J].ProceedingsoftheInstitutionofMechanicalEngineers, 1970, 185(1): 625-633. [3]ChangW,EtsionI,BogyDB.AnElastic-plasticModelfortheContactofRoughSurfaces[J].JournalofTribology, 1987, 109(2): 257-263. [4]杨红平, 傅卫平, 王雯, 等. 基于分形几何与接触力学理论的结合面法向接触刚度计算模型[J]. 机械工程学报, 2013,49(1):102-107. YangHongping,FuWeiping,WangWen,etal.CalculationModeloftheNormalContactStiffnessofJointsBasedontheFractalGeometryandContactTheory[J].JournalofMechanicalEngineering, 2013, 49(1):102-107. [5]田红亮, 钟先友, 秦红玲, 等. 依据各向异性分形几何理论的固定结合部法向接触力学模型[J]. 机械工程学报, 2013, 49(21): 108-122. TianHongliang,ZhongXianyou,QinHongling,etal.NormalContactMechanicsModelofFixedJointInterfaceAdoptingAnisotropicFractalGeometricalTheory[J].JournalofMechanicalEngineering, 2013, 49(21): 108-122. [6]尤晋闽, 陈天宁. 结合面法向动态参数的分形模型[J]. 西安交通大学学报, 2009, 43(9): 91-94. YouJinmin,ChenTianning.FractalModelforNormalDynamicParametersofJointSurfaces[J].JournalofXi’anJiaotongUniversity, 2009, 43(9): 91-94. [7]温淑花, 张学良, 武美先, 等. 结合面法向接触刚度分形模型建立与仿真[J]. 农业机械学报, 2009, 40(11): 197-202. WenShuhua,ZhangXueliang,WuMeixian,etal.FractalModelandSimulationofNormalContactStiffnessofJointInterfacesandItsSimulation[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2009, 40(11): 197-202. [8]ZhaoYW,MaiettaDM,ChangL.AnAsperityMicroContactModelIncorporatingtheTransitionfromElasticDeformationtoFullyPlasticFlow[J].JournalofTribology, 2000, 122(1): 86-93. [9]赵永武,吕彦明,蒋建忠. 新的粗糙表面弹塑性接触模型[J]. 机械工程学报, 2007, 43(3): 95-101. ZhaoYongwu,LüYanming,JiangJianzhong.NewElastic-plasticModelfortheContactofRoughSurface[J].JournalofMechanicalEngineering, 2007, 43(3): 95-101. [10]BrakeM.AnAnalyticalElastic-perfectlyPlasticContactModel[J].InternationalJournalofSolidsandStructures, 2012, 49(22): 3129-3141. [11]徐超,王东.一种改进的粗糙表面法向弹塑性接触解析模型[J].西安交通大学学报, 2014, 48(11): 115-121. XuChao,WangDong.AnImprovedAnalyticalModelforNormalElastic-PlasticContactofRoughSurfaces[J].JournalofXi’anJiaotongUniversity, 2014, 48(11): 115-121. [12]KogutL,EtsionI.AFiniteElementBasedElastic-plasticModelfortheContactofRoughSurfaces[J].TribologyTransactions, 2003, 46(3): 383-390. [13]张学良, 王南山, 温淑花, 等. 机械结合面切向接触阻尼能量耗散弹塑性分形模型[J]. 机械工程学报, 2013, 49(12):43-49. ZhangXueliang,WangNanshan,WenShuhua,etal.ElastoplasticFractalModelforTangentialContactDampingEnergyDissipationofMachineJointInterfaces[J].JournalofMechanicalEngineering, 2013, 49(12):43-49. [14]JacksonRL,GreenI.AFiniteElementStudyofElasto-plasticHemisphericalContactagainstaRigidFlat[J].J.Tribol., 2005, 127: 343-354. [15]StanislawKucharski,GrzegorzStarzynski.StudyofContactofRoughSurfaces:ModelingandExperiment[J].Wear, 2014, 311: 167-179. [16]McCoolJI.ComparisonofModelsfortheContactofRoughSurfaces[J].Wear, 1986, 107(1):37-60. [17]TaborD.TheHardnessofMetals[M].Oxford:OxfordUniversityPress, 1951. (编辑卢湘帆) NormalContactModelofRoughSurfacesBasedonTrueStress-StrainRelationship WangShijunYangChaoWangShiyiYangHuixinZhaoJinjuanLiShujuanLiPengyang Xi’anUniversityofTechnology,Xi’an,710048 Amodelingmethodfornormalelastic-plasticcontactofroughsurfaceswaspresented.Basedonelastic-plasticfiniteelementcontactmodelofasperity,normalcontactcharacteristicsbetweenasperitiesof40Cr, 45,Q235andrigidplanewerestudiedrespectively.Infiniteelementmodel,thetruestress-strainrelationshipsofthethreematerialswereusedandtheinfluencesofthedifferenthardeningbehaviorsoncontactcharacteristicsofasperitywereinvestigated.Asaresult,unifiedfunctionexpressionsofcontactvariablesofasperitywerebuiltinthreestages:elastic,elastic-plastic,plasticdeformation.Basedonthecontactanalysisofasperity,anormalelastic-plasticcontactmodelofroughsurfaceswasbuiltbyprobabilisticstatisticsmethod.Bythepresentedmethod,thechangesofcontactvariablesofasperityinthecontactmodeldependedentirelyonresultsofelastic-plasticfiniteelementanditwasunnecessarytodividethedeformationprocessofasperityintodifferentdeformationstages,whichavoidednon-continuityandnon-smoothnessofcontactvariablesbetweendifferentstagesandarbitrarinessofchoiceofinterpolationfunctioninelastic-plasticdeformationstage.Comparedwithothercontactmodels,thecalculatedresultsofthemodelareconfirmed. roughsurface;normal;elastic-plasticdeformation;contactmodel 2015-10-12 国家自然科学基金资助项目(51145720);陕西省科技厅科技统筹创新工程重点实验室资助项目(2014SZS10-P05) O343.3 10.3969/j.issn.1004-132X.2016.16.004 王世军,男,1967年生。西安理工大学机械与精密仪器学院副教授。主要研究方向为机械结合部特性。发表论文40余篇。杨超,男,1988年生。西安理工大学机械与精密仪器学院硕士研究生。王诗义,男,1989年生。西安理工大学机械与精密仪器学院硕士研究生。杨慧新,男,1992年生。西安理工大学机械与精密仪器学院硕士研究生。赵金娟,女,1974年生。西安理工大学印刷包装工程学院讲师。李淑娟,女,1968年生。西安理工大学机械与精密仪器学院教授、博士研究生导师。李鹏阳,男,1972年生。西安理工大学机械与精密仪器学院副教授。



2 粗糙表面的接触模型
3 模型的验证


4 结语
