图像混沌加密算法的密码破译与算法改进

韩 凤 英

(空军航空维修技术学院　湖南 长沙410014 )



图像混沌加密算法的密码破译与算法改进

韩 凤 英

(空军航空维修技术学院湖南 长沙410014 )

针对文献中提出的一种基于位置和像素值变换的图像混沌加密新算法，分析算法的缺陷并提出对该算法的一种选择明文攻击方法，展示明文图像可以不需要原始密钥而能准确地从密文图像恢复出来，因而该算法不具备在网络通信中应用所需的足够安全性，并提出一种更加安全的改进算法。理论分析和实验结果表明：改进算法不仅克服了原算法的那些缺陷，而且具有更好的密码学性能。

图像加密混沌系统密码分析选择明文攻击

0　引　言

数字图像作为一种重要数字媒体信息在当今得到了广泛的应用。随着网络通信技术的迅猛发展，数字图像在信息交换、存储和通信中使用频繁。然而，信息存储和通信环节存在的诸多不安全因素对许多重要信息构成威胁。为了保证军事信息、政府机密文件、商业秘密、个人隐私等重要信息的安全，通常会对信息进行加密处理。而图像具有数据量大、相邻像素相关性强、数据冗余多等特点[1，2]，不适合采用传统的加密方式。而混沌系统具有对初始条件的敏感性，参数可控性、伪随机性，且在一定的周期内具有唯一性，所以适合于数字图像加密。许多专家学者提出了很多基于混沌系统的图像加密算法[3-6]，而对于基于混沌系统的图像加密算法的安全性分析研究较少。如果对于存在安全隐患的加密算法，不加以指出，应用到工程实践中，将会带来安全隐患，造成不可估量的影响。本文研究了文献[11]中所提出的基于位置和灰度变换的混沌图像置乱算法，发现了算法中存在的安全漏洞，并利用选择明文攻击，成功地破解了该算法密码。并基于该算法，提出一种改进算法，改进后的算法克服了原算法的缺陷，安全性得到了提高。实验证明，本文改进的算法具有更好的密码学性能。

1　原密码算法的分析与破解

1.1原算法简述

文献[11]中采用如式(1)所示的经典的混沌系统Logistic映射作为混沌加密系统。

xn+1=μxn(1-xn)

(1)

其中,x为系统变量，μ为系统参数，当u=4时，式(1)所生成的序列在区间(0，1)上具有混沌遍历性。在文献[11]中，以x0为式(1)的初值，生成混沌密钥序列。

用x表示原始明文图像加的像素点的灰度值，其中0≤x≤255。用y表示用式(1)生成的混沌序列中的某个状态值经过处理后得到整数值，其中0≤y≤255。文献[11]利用式(2)对原始图像即明文图像的像素值x进行加密变换后得到密文像素值z：

z=mod(x+y,256)

(2)

式(2)中mod()表示取模，由式(2)可以推导出式(3)所示的像素值解密公式。

x=mod(z-y+256,256)

(3)

用数组A表示图像的灰度图像矩阵，A(i，j)表示第i行第j列处的像素点灰度值。若图像的大小为M×N，那么i=1，2，…，M，j=1，2，…，N。对图像像素按行优先次序依次扫描，设像素的序号用k表示，k=1，2，…，M×N。则由像素序号k计算该像素的行号i、列号j的公式为：

(4)

其中，|-x-|表示取大于或等于x的最小整数。利用式(1)生成的混沌序列在文献[11]中有两个用途：其一是利用状态值x来产生一个[2，M×N]范围的整数k，k值就是当前欲移动的像素原所在位置的序号；其二是利用状态值x来产生另一个[0，255]范围的整数y，y值用来作为像素值替代变换的密钥。设Visited用来标识像素是否已经移动，初值为0，表示没有移动，若待加密的原始明文图像的大小为M×N，那么Visited的大小为M×N；同时设置一个count变量用于记录已经移动的像素数目。每移动一个像素时，将相应位置的Visited数组元素值修改为1，同时count值增1。每当一个像素值移到新位置后，立刻用式(2)对其像素值进行替代加密。

1.2原算法密码的破译

一个安全的密码算法必须能够抵抗选择明(密)文攻击、选择明文攻击、已知明文攻击、唯密文攻击。下面通过选择明文攻击来破解文献[11]中所提出的加密算法。

因为在原算法中，灰度变换密钥完全由混沌序列的初始密钥而决定，与待加密的图像无关；而位置置乱也完全由混沌序列密钥决定，也与待加密的明文图像无关。所以利用混沌序列对任何图像进行加密，替代和置乱规律都是相同的。所以只要能够选择明文攻击，计算出混沌序列，进而可以解密出任何利用该混沌序列进行加密的图像。

文献[11]中的算法位置变换如式(5)所示，像素值变换如式(6)所示：

B(1)=A(k1)B(ki)=A(ki+1)B(kM×N-1)=A(1)

(5)

i=1，2，…，M×N-2

C(n)=mod(B(n)+yn,256)n=1，2，…，M×N

(6)其中,A(n)表示原始明文图像、B(n)表示位置变化图像、C(n)分最终密文图像。n表示按行优先次序一维化后所得的序列值。

设截获了一个用文献[11]算法加密的2×3大小的密文图像，其像素按行优先次序一维化的数组为C={119，124,57，10，110，228}。假设对应于选择明文数组Ap={0，0，0，0，0，0}，得到的密文数组为Cp={110，135，2，255，12，254}；又对应于选择明文数组Aq={1，2，3，4，5，6}，得到的密文数组为Cq={137，8，0，17，4}。要求破译出密文图像C所对应的明文图像A。

(1) 因Ap元素全是零，故Bp={0，0，0，0，0，0}；所以，Y=Cp={110，135，2，255，12，254}。

(2) 由Cq={115，139，8，0，15，0}和Y= {110，135，2，255，12，254}，可以求出破译的中间版本：

Bq={mod(Cq(n)-yn+256，256)，n=1，2，…，6}={5，4，6，1，3，2}。 因为Bq(1) =Aq(5)，所以k1=5；因为Bq(k1) =Bq(5) =Aq(3)，所以k2=3； 因为Bq(k2) =Bq(3) =Aq(6)，所以k3=6； 因为Bq(k3) =Bq(6) =Aq(2)，所以k4=2；因为Bq(k4) =Bq(2) =Aq(4)，所以k5=4；而Bq(k5) =Aq(1)。故，K={5，3，6，2，4}。

(3) 解密C，由C={119，124，57，10，110，228}和Y= {110，135，2，255，12，254}，可求得：B={mod(C(n)-yn+256，256),n=1，2，…，6}={9，245，55，11，98，230}；再根据K={5，3，6，2，4}，因为k1=5，B(1) =A(k1)，所以A(5)=9；因为k2=3，B(k1)=A(k2),所以A(3)=B(5)=98；因为k3=6，B(k2)=A(k3),所以A(6)=B(3)=55；因为k4=2，B(k3)=A(k4),所以A(2)=B(6)=230；因为k5=4，B(k4)=A(k5)，所以A(4)=B(2)=245；因为B(k5)=A(1)，所以A(1)=B(4)=11。于是得到解密出来的图像数组为：A={11，230，98，245，9，55}。

由此可知，通过两组选择的明—密文对进行密码分析，就能破译出原算法中等价的中间密钥序列；而等价的中间密钥序列与被加密图像内容无关，所以文献[11]的密码算法不能抵御选择明文攻击。

2　改进算法

原算法具有如下优点：置乱与替代结构清晰、简单，像素位置置乱过程确保了每个像素都发生位置移动且只移动一次，因此，不动点数目为0，置乱效率高。但存在如下缺陷：图像加密算法中的像素值替换与像素位置变化两个环节都与原始明文图像无关，所以算法不能抵抗选择明(密)文攻击。此外，算法中关于像素值替代加密的公式所具有的密码学性能不优，一是针对式(2)利用已知的明—密文对易于破解出替代密钥序列Y；二是该算法产生的密文在分布性、相邻像素的相关性、对明文的敏感性和密文信息熵等方面尚都存在很大的优化空间。基于此，本文提出一种既能抵抗选择明(密)文攻击，又具有更优密码学性能的改进算法。

2.1加密算法

设像素为M行、N列的明文灰度图像矩阵为A，其像素总数为M×N。算法原始密钥集为{x0，y0，N0，C0，Y0}，其中，双精度实数x0和y0作为Logistic系统的两种初始状态值，N0是一个500以上的整数，C0和Y0都是[0，255]范围的整数。改进算法将像素位置置乱与像素值替代两类操作分开，位置置乱过程的基本思想是：由x0生成与明文相关的混沌序列，再由混沌序列随机产生范围在[1，M×N]之内的整数km，然后依次将序号为m(m=1，2，…，M×N)的像素移动到序号为km的位置(km≠m)。像素值替代加密的密钥由y0生成的混沌序列产生。

算法输入：明文图像矩阵AM×N，初始密钥{x0，y0，N0，C0，Y0}；

算法输出：密文图像矩阵CM×N。

像素位置置乱算法的具体步骤描述如下：

1) 设置一个长度为M×N的一维标志数组F，并初始化：F(i)=0，i=1，2，…，M×N。 令：m=1。

2) 求明文图像A全部元素按位异或运算的值s；并按s值修改Logistic系统的初始值x0：x0=(s/256)×x0。使x0与图像内容相关。

3) 由式(1)生成新的混沌序列值x，根据x的值计算出t值和k值，其中t=round(x×1012)，k=mod(t，M×N)+1。

4) 若F(k)为1(表示整数k已经产生过)或k等于m，则转到步骤3)继续执行，直至产生的k满足：F(k)值是0，且k不等于m。

5) 将A中序号为m的元素移动到序号为k的位置：B(row，col)=A(i，j)，其中，(i，j)是A中第m个像素的行列号，(row，col)是B中第k个像素的行列号；同时置F(k)值为1(表示k已经产生过)。

6) 若m≤M×N，则转到步骤3)，继续循环执行步骤3)到步骤5)。

像素值替代加密算法的具体步骤描述如下：

1) 初始化：选取经过替代变化后的加密图像的第M和第N个像素点的像素值分另赋给C0和Y0，令C1=C0，Y1=Y0，m=1。

2) 混沌系统式(1)从初值y0开始迭代(N0+M×N)次，对生成的y序列舍弃前N0个值，取后面长度为M×N的子序列，并将子序列的实数值按式(7)转换成整数序列(1≤y(n)≤255)：

y(n)=mod(round(y(n)×1012),255)+1

n=1，2，…，M×N-1

(7)

3) 将m值转换为相应的行、列号i和j，先按式(8)对第m个像素进行替代加密，然后按式(9)修改C1、Y1、m的值。

C(i,j)=mod(B(i,j)⊕y(m)+C1⊕Y1,256)

(8)

C1=C(i,j),Y1=y(m),m=m+1

(9)

4) 若m≤M×N，则转到步骤3)继续循环执行； 否则，输出密文矩阵C，算法结束。

2.2解密算法

算法输入：密文图像矩阵CM×N，初始密钥集{x0，y0，N0，C0，Y0}；

算法输出：明文图像矩阵AM×N。

首先，对密文像素值进行反替代操作，操作步骤与前面的密文像素值替代操作类似，只是将式(8)改为下列求解B(i，j)的式(10)：

B(i,j)=(mod(C(i,j)-C1⊕Y1+256,256))⊕y(m))

(10)

然后，对密文像素的位置进行反置乱操作，操作步骤也与前面的密文像素位置的置乱操作类似，只是将公式B(row，col)=A(i，j)改为求解A(i，j)的公式：A(i，j)=B(row，col)。

3　仿真实验与安全性分析

在仿真实验中采用标准Lena图像(256×256×8位)，用Matlab 7.1对算法实验进行仿真测试。设混沌序列的初值及参数值为：C0=68，Y0=24，N0=600，x0=0.543，y0=0.403。

3.1密钥空间与抗攻击性能分析

改进算法相比原算法，初始密钥增加了4个(C0、Y0、N0和y0)。假设N0可能取值个数为500，C0、Y0可能取值个数各为255，双精度实数x0和y0各为15位小数，则密钥空间为500×255×255×1015×1015≈2125。如此大的密钥空间，足以抵抗穷举攻击。

改进算法所产生的置乱序列{km|m=1，2，…，M×N}与被加密图像内容相关，这将使选择明(密)文攻击方法失效。因为，改进算法中，待解密的密文图像的变换序列与明文图像的变换序列不相同，所以即便用选择明文攻击得出等价的位置变换密钥序列，也不可能破解密文图像。另外，改进了像素置乱方式和像素值替代加密方法。特别地，在式(8)中通过引入参数C1(代表前一点的密文)和Y1(代表前一个密钥)，一方面使加密过程产生信息扩散机制。另一方面，使同一公式中包含了两个密钥y(m)和Y1，这样，攻击者即使用已知的B(i，j)-C(i，j)数据对也无法唯一确定y(m)和Y1。故不能用选择明(密)文攻击法破解y(m)序列，也说明本文的改进算法具有抵抗选择明(密)文攻击的能力。

3.2加密效果测试

明文图像为图1(a)，改进算法的加密图像为图1(b)，可以看出加密后的图像杂乱无章，看不出任何明文图像内容，图像类似于噪声。

图1　明文图像和加密图像

明文图像和密文图像对应的直方图分别如图2所示。由(a)可知，明文图像的像素值在[0,255]的区间中分布非常不均匀；由(b)可知，文献[11]的算法生成的加密图的直方图比(a)稍均匀，但是还不太理想； 由(c)可知本文的改进算法生成的加密图的直方图分布非常均匀。因此，改进算法具有抵抗统计分析攻击的能力。

(a) 明文图像的直方图

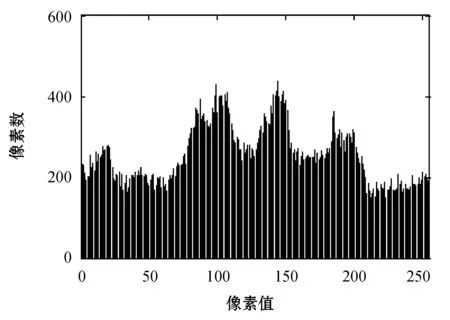
(b) 原算法加密图像的直方图

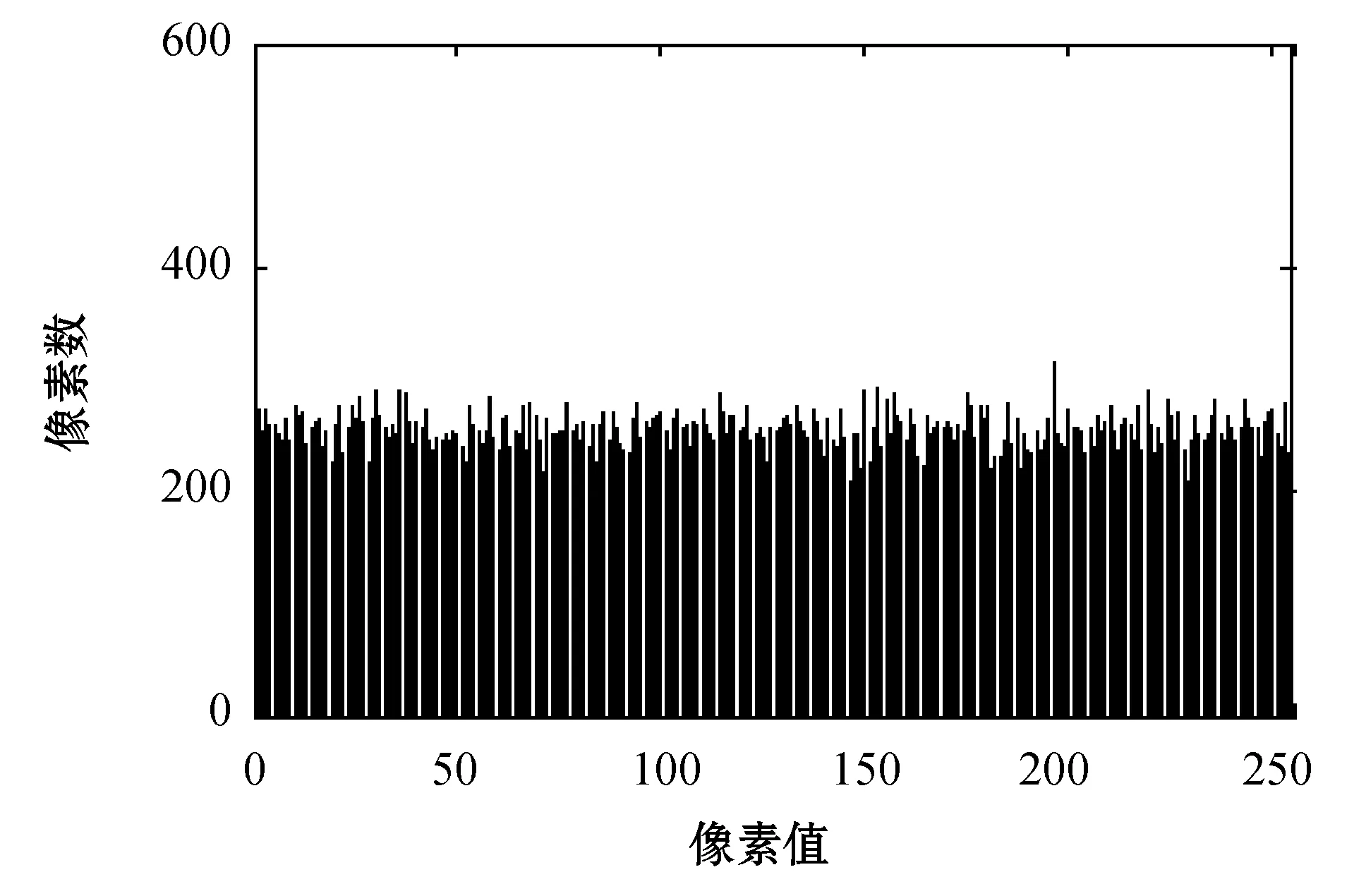
(c) 改进算法加密图像的直方图图2　明文和密文图像的直方图

3.3相关性测试

相邻像素之间的相关程度可以用相邻像素之间的相关系数来衡量。相邻像素之间的相关系数计算如下：

(11)

(12)

(13)

(14)

其中，x和y表示图像中相邻2个像素的像素值，γxy为图像相邻两个像素的相关系数。选择水平、垂直、对角三个方向的全部相邻像素，采用式(14)计算出相关系数。如表1所示，原始明文图像相邻像素点具有高相关性，其相关系数非常接近1；本文所设计的加密算法生成的密文图像相邻像素几乎不相关，相关性接近于0；而其他几个文献中的相邻像素的相关性也高于采用本文所设计加密算法得到的加密图像的相关性。

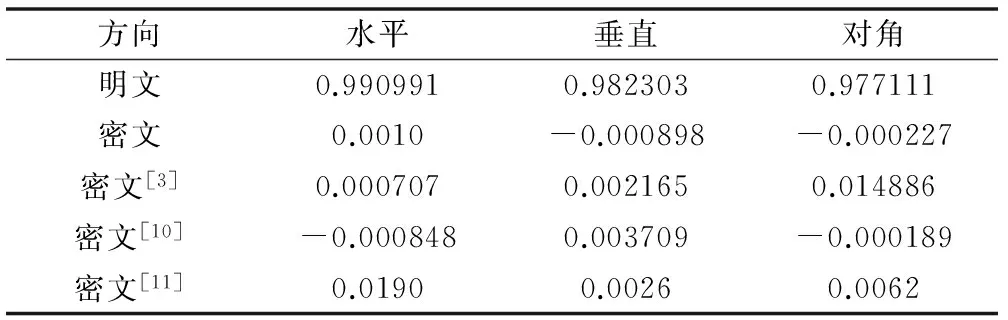
表1　明文和密文图像中相邻像素的相关系数

3.4敏感性测试

如果明文或密钥的微小变化就引起密文的变化越大，则说明算法的敏感性越强，也说明算法的抗差分攻击能力越强。度量算法的敏感性通常用NPCR(可用像素改变率)和UACI(归一化平均改变强度)两个参数，可以采用文献[10]中的方法计算。NPCR与UACI的计算都是在明文图像只改变了一个像素时，密文图像的改变程度。对8位灰度图像，这两个值的理想期望值是NPCR=99.6094%，UACI= 33.4635%。

由文献[11]的算法可知，该算法对明文是不敏感的，因为明文中一个像素发生变化，只可能引起密文中一个像素变化。在本实验中选择5组明文图像来验证改进算法的明密文敏感性。每组第1幅明文图像是原始Lena图像，第2幅明文图像是将原始Lena图像其中一个像素的值增加1，这个被改变的像素所在位置包含了最前、中间、末尾三种极端情况。根据文献[10]中的计算方法计算出NPCR和UACI值，见表2。由表2的结果可知，这两个值都非常接近理想期望值，这表明密文对明文高度敏感性。

表2　几组密文图像之间的NPCR和UACI值

为验证密文对初始密钥的敏感性，我们分别对两组密钥中的x0与y0改变10-10(其他密钥不变)，然后用两组密钥分别加密同一幅Lena图像。当仅有x0改变10-10时，所得两幅密文图像的NPCR和UACI值分别是0.9959和0.3341，图3(a)给出了两幅密文图像前100个像素的差值曲线。当仅有y0改变10-10时，所得两幅密文图像的NPCR和UACI值分别是0.9959和0.3351，图3(b)给出了两幅密文图像前100个像素的差值曲线。可见，密文对密钥x0和y0是充分敏感的。进一步的实验也证实了密文对密钥C0、Y0和N0也充分敏感。

图3　密文对密钥的敏感性测试结果

4　结　语

(1) 对文献[11]提出的混沌图像加密算法分析了存在的安全缺陷，通过选择明文攻击破译了该算法。

(2) 提出了一种改进型置乱—替代结构图像混沌加密新算法。使像素位置置乱序列的产生不仅依赖于混沌密钥，而且与明文相关；像素值替代变换的加密过程同时引入了密文扩散和双密钥参与机制，有效地提高了算法的安全性。

(3) 对改进算法进行了详尽的实验测试和安全性分析，证明了改进算法具有很强的抗选择明(密)文攻击和穷举攻击的性能；而且密文直方图分布均匀，算法对明密文敏感，加密图的相邻像素的相关系数近于0。

因此本文提出的改进算法具有更好的密码学特性，更适合应用在数字图像的保密通信及安全存储中。

[1] 廖晓峰,肖迪,陈勇,等.混沌密码学原理及其应用[M].北京:科学出版社，2009:37-39.

[2] Mazloom S，Eftekhari-Moghadam A M.Color image encryption based on Coupled Nonlinear Chaotic Map[J].Chaos,Solitons and Fractals，2009，42(3):1745-1754.

[3] Wang Y,Wong K W,Liao X,et al.A new chaos-based fast image encryption algorithm[J].Applied Soft Computing,2011，11(1):514-522.

[4] Zhang Guochao,Liu Shaohui,Jiang Feng,et al.An improved image compression scheme with an adaptive arameter set in encrypted domain[J].Visual Communications an Image Processing,2013,9(1):1-6.

[5] 谢凯明，邓家先，陈益刚.基于JPEG2000的图像联合压缩加密算法[J].计算机应用研究，2014，31(12)：3695-3699.

[6] 卢守东,肖芳雄.基于三维混沌系统的通用数字图像加密与恢复算法[J].计算机应用与软件,2013,30(12):87-92.

[7] Zhu Congxu,Liao Chunlong,Deng Xiaoheng.Breaking and improving an image encryption scheme based on total shuffling scheme[J].Nonlinear Dynamics,2013,71(1-2):25-34.

[8] Rhouma Rhouma，Safya Belghith.Cryptanalysis of a new image encryption algorithm based on hyper-chaos[J].Physics Letters A，2008，372(38):5973-5978.

[9] Gao T,Chen Z.A new image encryption algorithm based on hyper-chaos[J].Physics Letters A,2008,372(4) :394-400.

[10] Zhang Guoji,Liu Qing.A novel image encryption method based on total shuffling scheme[J].Optics Communications,2011,284(12):2775-2780.

[11] 王青松，范铁生.基于位置和灰度变换的混沌图像置乱算法[J].小型微型计算机系统，2012，33(6):1284-1288.

CODE BREAKING FOR IMAGE CHAOTIC ENCRYPTION ALGORITHM AND ALGORITHM IMPROVEMENT

Han Fengying

(AirForceAeronauticalCollege，Changsha410014,Hunan,China)

Aiming at the new algorithm of image chaotic encryption based on location and pixel gray transformation proposed in the literature,we analysed the flaws of the algorithm and presented an attack method against it by choosing the plaintext,and showed that the plaintext image can be recovered exactly from the cipher image without the need of original key,therefore the algorithm is not secure enough to be applied in network communication,and proposed an improved algorithm which is more secure.Theoretical analysis and experimental results all showed that the improved algorithm can overcome these flaws and has better cryptographic performances as well.

Image encryptionChaotic systemCryptanalysisChoosing plaintext attack

2015-02-09。国家自然科学基金项目(61073187);湖南省教育厅科研项目(13C995)。韩凤英，副教授，主研领域：信息安全。

TP309.7

A

10.3969/j.issn.1000-386x.2016.08.065