对无临近点信息干涉条纹的参数估计

王超，王忠康



对无临近点信息干涉条纹的参数估计

王超，王忠康

(杭州应用声学研究所，浙江杭州310023)

用广义radon变换可以从运动目标产生的干涉条纹中估计出目标的运动参数和波导不变量。但是当干涉条纹中没有出现临近点时，用此方法估计不出真实值。为了解决此问题，提出了一种新的估计方法。主要过程是先从时频图中提取出干涉条纹轨迹，再去搜索与此轨迹误差最小的最优曲线，此曲线的参数值代表目标的运动参数和波导不变量。仿真和海试结果表明，在干涉条纹无临近点信息情况下，用广义radon变换估计的参数值与真实值偏差很大，但是文中提出的方法仍能估计出较准确的结果。

干涉条纹；无临近点信息；广义radon变换；宽容性参数估计；波导不变量

0 引言

低频声场中存在稳定的干涉结构，并且随着频率的改变干涉结构中的极值会产生偏移，这个在距离上的偏移量和频率的关系可以用波导不变量来描述，即用来描述域干涉条纹的斜率[1]。虽然的值随着海洋环境的改变而变化，但是在大部分浅水波导环境中可以近似为1[2]。

对于运动目标(假设目标做匀速直线运动)，它到接收水听器的距离一直在变化，所以其辐射的宽带噪声中能观察到倾斜的干涉条纹。而对接收数据进行分析，只能得到信号的时频域信息，但由于运动目标的距离随时间变化，所以域与域相关联，它们的关系由声源相对于接收水听器的相对速度决定。如果运动目标的轨迹经过接收水听器，那么其在时频域的干涉条纹是一族类双曲线。这些曲线中包含有波导不变量、(为目标最近通过距离，为目标航向速度)、(为目标到达临近点的时间)等信息。其中若已知，就可以求得声源的距离和速度[3-4]，准确的值对于速度和距离求解十分重要。图1是用海试数据处理以后得到的时频图(LOFAR)，从中可以看到清晰的类双曲线干涉条纹。而双曲线顶点对应的时间就是目标离接收点最近的时间。

文献[1]中已指出用广义radon变换可以提取出上述信息。但是如果时频图中没有完整的干涉条纹，即在已有的信号接收时间内，目标一直在靠近或者远离接收水听器，并没有经过它。此时直接用广义radon变换进行分析效果会变得很差，本文提出了一种方法可以在很大程度上减小误差，从没有顶点信息的干涉条纹中提取参数，并进行了仿真和海试分析。

1 运动目标的干涉条纹分析

先建立一个运动模型，假设目标做匀速直线运动。接收水听器位于坐标原点。目标运动过程中辐射宽带连续谱信号，其线速度为，最近通过距离为，最近通过时刻为，其航迹几何关系如图2所示。

由几何关系可知目标运动轨迹方程为:

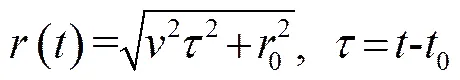
由式(1)可得

(2)

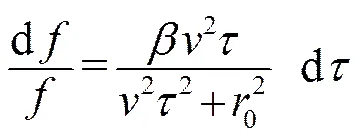
两边积分，整理得

(4)

广义radon变换可以检测图像中的任意曲线。它是将图像空间中同一曲线上的点映射到参数空间交于一点的一族曲线，交点的位置反映了图像空间该曲线的参数[4]。图1所示图像中亮纹的集合表示为：

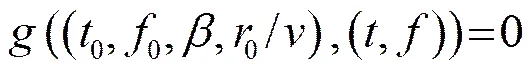
2 无临近点干涉条纹参数估计

下面以海试数据图1为例分析以上过程，假设只有图1中1440 s以内的数据，并且分析的频率段在50～200 Hz之间。经时频分析求出接收信号的时频图如图4所示，提取出77 Hz对应的亮纹，结果如图5所示。

在参数估计过程中，只要估计的参数值处于图6所示的限定区间之内都认为是合理的。超出限定区间的部分被认为是误差[5]。下面考虑用二次代价函数，即，误差可表示为

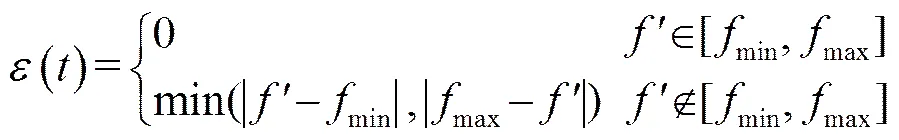
(7)

为了减小搜索过程的运算量和误差，可先根据条纹线的特性在搜索过程进行剪枝筛选。若由搜索参数值确定的线不满足条纹特性，就不再计算该搜索值对应的误差，直接认为这组参数不是真实值。亮纹的产生是由于目标运动导致不同时刻声源与接收点距离发生改变而产生的。当目标按图2所示的轨迹运动，且，目标由远及近向接收点运动时，它的距离变化率一直在减少，即相对速度减小。此时反映在干涉条纹上就是条纹斜率的绝对值一直在减小，也就是说干涉条纹对应的函数是个下凸函数。所以用式(8)来对搜索线进行筛选：

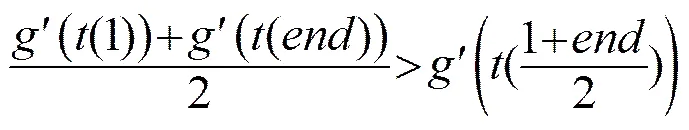
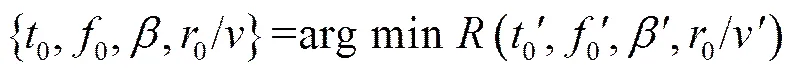
3 仿真和海试结果分析

由于处理的频带是300 Hz以下的低频目标，仿真过程中用kraken模型计算出运动目标的接收信息，然后用第2节所示的方法进行处理。具体的仿真环境为等声速波导，声速为1525 m/s，深度为100 m；采用粗粒砂底，具体参数为：底部声速1836 m/s，密度，底部损失=；收发设备分别在80 m和40 m。目标的运动模型如图2所示，其速度=2.5 m/s，最近距离=1250 m，最近通过时间=1728 s。此环境下，。考虑50～300 Hz这一频段内的数据。时频图如图7所示。

首先对有完整干涉条纹的情况用广义radon变换进行分析，其中(，)为亮纹顶点，是已知的，主要估计参数为、。估计结果如图8所示。

接下来分析没有亮纹顶点信息时的参数提取，图9即为要处理的时频图，它只有1440 s以内的数据。

然后用第2节提到的方法来进行分析，首先提取出亮纹，如图10所示，这里选择的是顶点频率在129 Hz的亮纹，然后提取出此亮纹所对应的区间，结果如图11所示。

估计过程中因为考虑了宽容性处理，用一条亮纹进行分析时，误差最小得到的结果可能有很多组不同参数值都对应着最小误差，此时考虑再找一条或多条亮纹进行分析，然后找出结果中出现次数最多的一组，作为估计的结果。本文考虑了168 Hz，113 Hz两条亮纹，最后得到的结果为，，。此结果与真实值相比已相当准确。

用海试数据进行分析，对图1所示的干涉条纹，直接用广义radon变换进行分析，此时和已知，为1728 s，为{77，95，109，125，153，184}Hz，对在区间[0，2]内搜索，的搜索范围在[100，1500]之间。对为不同值的结果进行求和便可得到估计的参数值。具体结果为，，的值符合浅海波导的理论值，所以此估计结果较为准确。分析不完整的干涉条纹，即如图4所示，、的搜索区间分别为[1500，2000]、[60，90]。用广义radon变换得到的结果为=1900 s，=62 Hz，，此结果明显误差较大。

下面用第2节提出的方法来分析，具体的过程图4~6所示，这里选用顶点频率为77 Hz的那条亮纹，估计出的结果为=1700 s,=76 Hz，。此结果中与真实值较为接近，与有顶点信息的估计结果相近，此结果可以接受。

4 总结

本文提出了一种针对干涉条纹的参数估计方法。文中先详细介绍了运动目标产生干涉条纹的原理，并指出用广义radon变换来分析干涉条纹中包含的运动参数信息。但是当干涉条纹不完整时，用此方法分析误差较大。本文方法先提取出要分析的亮纹，然后构造一个代价函数，再利用干涉条纹的下凸特性进行剪枝搜索，搜索得到的最优解代表目标的运动参数和波导不变量。在干涉条纹无临近点信息时，此方法与广义radon变换进行对比可很大程度上减小误差。仿真和海试都验证验证了此方法的可行性。

[1] Jensen F B, Kuperman W A, Porter M B, et al. Computational ocean acoustics[M]. 2nd ed. New York, 2011.

[2] Cockrell K L. Understanding and utilizing waveguide invariant range-frequency striations in ocean acoustic waveguides[D]. Massachusetts Institute of Technology, 2011.

[3] 余赟, 惠俊英, 赵安邦, 等. 波导不变量及双阵元被动测距方法研究[J]. 兵工学报, 2011, 32(3): 274-280.

YU Yun, HUI Junying, ZHAO An-bang, et al. Waveguide Invariant and Passive Ranging Using Double Elements[J]. Acta Armamentarii, 2011, 32(3): 274-280.

[4] Turgut A, Rouseff D. Broadband source localization using horizontal-beam acoustic intensity striations[J]. J Acoust Soc Am, 2010, 127(1): 73-83.

[5] Kay S M. Fundamentals of statistical signal processing: estimation theory[M]. New Jersey: Prentice Hall, 1993.

Parameter estimation from interference striations under no information on the most approaching point

WANG Chao, WANG Zhong-kang

(Hangzhou Applied Acoustic Institute, Hangzhou 310023,Zhejiang,China)

An interference structure can be observed in low frequency continuous spectral sound field. The interference striations are a set of quasi hyperbolas as the source goes through the receiving hydrophone. The motion parameter of the source and the waveguide invariant can be estimated by using generalized radon transforms. The vertex of the quasi hyperbola represents the closest distance between source and receiving hydrophone, and the vertex is called the most approaching point (MAP). The generalized radon transforms need the vertex information, namely0and0(0is the time of the target arriving at MAP and0is the corresponding frequency at the quasi hyperbolas vertex). Without the vertex information, the estimation error is large. This paper presents a new way to estimate parameters under no information on MAP. In this way, the trajectory of the interference striation is first extracted for subsequently searching out the optimal parameter values. The error can be represented by a tolerance cost function. The simulation and sea-trial results show that this method can get an accurate result of parameter estimation under no information on the most approaching point.

interference striation; without the information of MAP; generalized radon transforms; robust parameter estimation;waveguide invariant

TB556

A

1000-3630(2016)-02-0162-05

10.16300/j.cnki.1000-3630.2016.02.014

2015-09-25;

2015-12-10

国家高技术研究发展计划(2011AA09A107)

王超(1989－), 男, 河南三门峡人, 硕士研究生, 研究方向为水声信号处理。

王超, E-mail: wangchaochim@foxmail.com